
·信号与系统sIgA18AS1S1卫MS 第七章离散信号与系统时域分析 ◆ 离散时间信号的定义以及典型的离散信号; ◆ 差分方程的建立与经典解法; ◆离散系统的单位样值响应; 零输入响应和零状态响应的概念; 如何求零输入响应; ◆如何利用卷积的方法求零状态响应
第七章 离散信号与系统时域分析 ◆ 离散时间信号的定义以及典型的离散信号; ◆ 差分方程的建立与经典解法; ◆ 离散系统的单位样值响应; ◆ 零输入响应和零状态响应的概念; ◆ 如何求零输入响应; ◆ 如何利用卷积的方法求零状态响应

·信号与系统SIGNAL84S1s1EM 6.1离散信号 一、离散时间信号 1、定义: 如果信号仅在一些离散的瞬间具有确定的数值, 则称之为离散时间信号。 一般用f(k)表示,其中k=0,±1,士2,.;T为离 散间隔。 把这种按一定规则有秩序排列的一系列数值称为 序列,简记为f(k)。常用序列{f(k}表示。 也可以用数据表格形式给出,或以图形方式表
6.1 离散信号 一、离散时间信号 1、定义: 如果信号仅在一些离散的瞬间具有确定的数值, 则称之为离散时间信号。 一般用f(kT)表示,其中k=0,±1,±2,.;T为离 散间隔。 把这种按一定规则有秩序排列的一系列数值称为 序列,简记为f(k)。常用序列{f(k)}表示。 也可以用数据表格形式给出,或以图形方式表
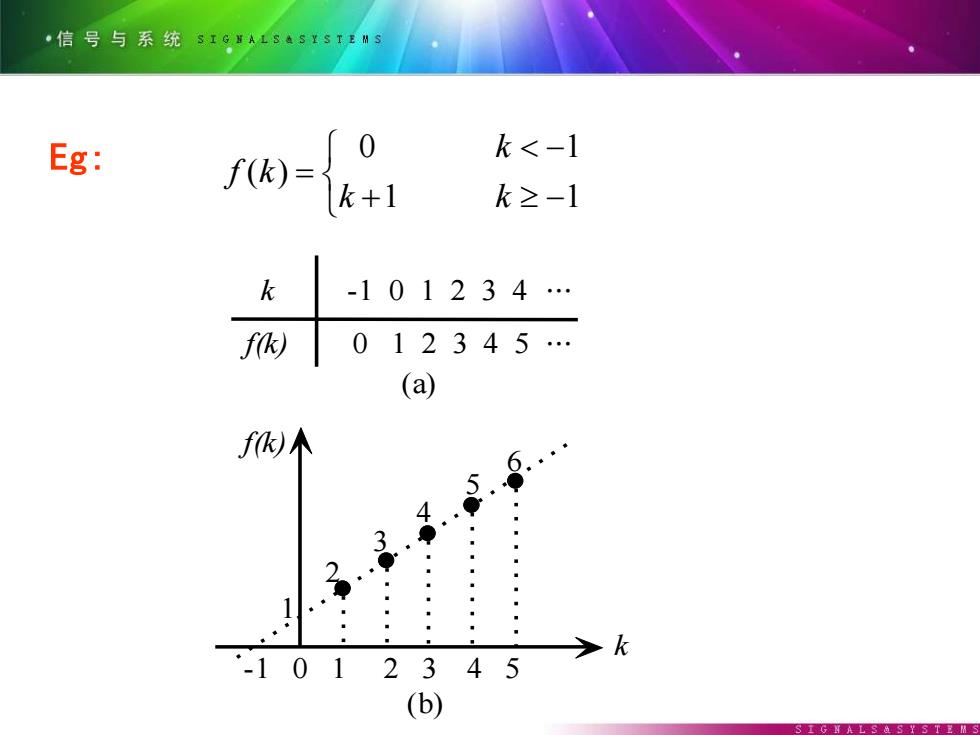
·信号与系统SIGALSAS¥S1卫Ms Eg: 0 f=k+1 k<-1 k≥-1 -101234. f012345. (a) f)不 6. J 4. . ● ◆ k -1012345 (b) S工GLS迪SXST起MS
Eg: 1 1 1 0 ( ) − − + = k k k f k k -1 0 1 2 3 4 f(k) 0 1 2 3 4 5 k f(k) 1 2 3 4 5 6 -1 0 1 2 3 4 5 (a) (b) 图 7 - 1

·信号与系统SIGNAL84S1S1ENS 2、离散时间信号的时域运算 (1) 相加 f(k)=f1(k)+f2(k) (2) 相乘 f(k)=f1(k)f2(k) (3) 数乘: y(k)=af(k) (4) 累加和: )=2f@
2、离散时间信号的时域运算 (1 : f(k)=f1(k)+f2(k) (2) 相乘 : f(k)=f1(k)f2(k) (3 : y(k) = af (k) (7-3) (4 =− = k i y(k) f (i) (7-4)
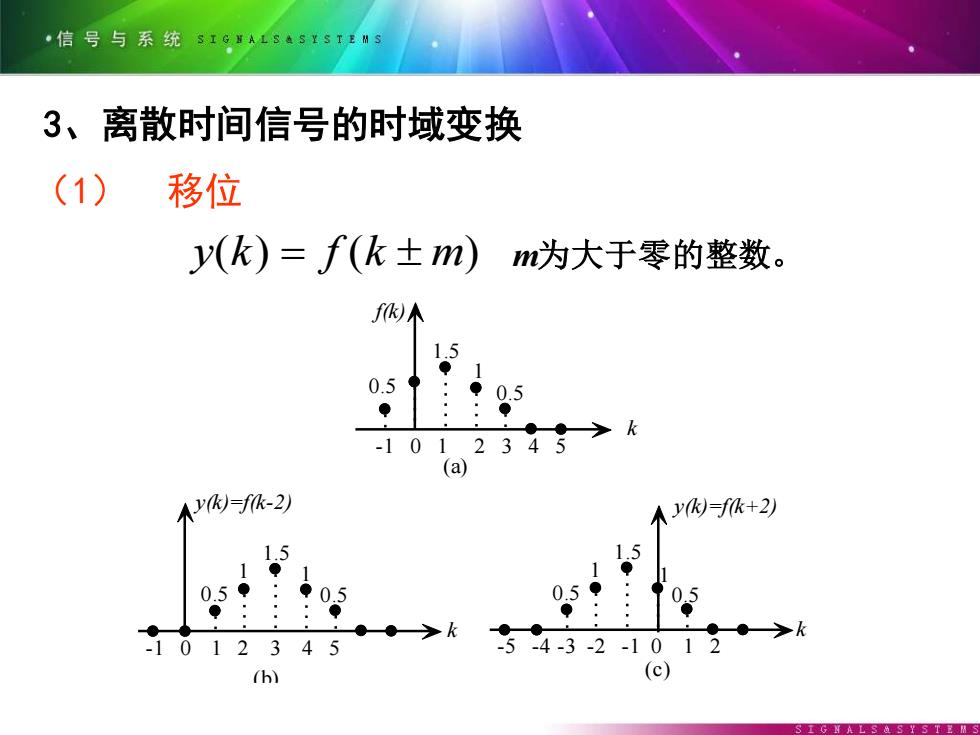
·信号与系统SIGNALSASYS1EMS 3、离散时间信号的时域变换 (1) 移位 y(k)=f(k±m)m为大于零的整数。 f)不 15 0.5 05 1012345>k (a) y=f-2) 人y因=f+2) 15 1.5 0.5 05 0.5 0.5 .0 12345 54-3-2-1012 (h) (c)
3、离散时间信号的时域变换 (1 y(k) = f (k m) m为大于零的整数。 (7-5) k f(k) 1.5 0.5 -1 0 1 2 3 4 5 0.5 1 (a) k y(k)=f(k-2) 1.5 0.5 1 2 3 4 5 1 1 0.5 -1 0 (b) k y(k)=f(k+2) 1.5 0.5 -3 -2 -1 0 1 2 1 1 0.5 -5 -4 (c) 图 7 - 3

·信号与系统SIGNAL84S1s1EM (2)折叠 y(k)=f(-k) (3)倒相 y(k)=-f(k) (4)展缩 y(k)=f(ak) 需要注意的是,对f()进行展缩变换后所得序列 y(k)可能会出现为非整数情况,在此情况下舍去这些 非整数的k及其值
(2)折叠 y(k) = f (−k) (7-6) (3)倒相 y(k) = − f (k) (7-7) (4)展缩 y(k) = f (ak) (7-8) 需要注意的是,对f(k)进行展缩变换后所得序列 y(k)可能会出现k为非整数情况,在此情况下舍去这些 非整数的k及其值
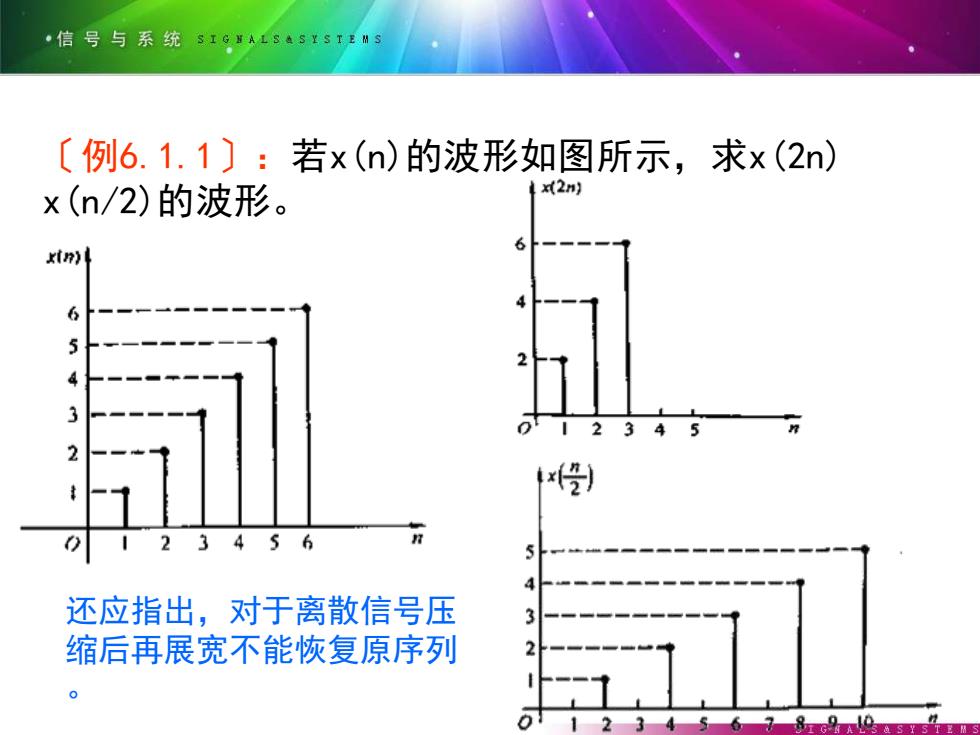
·信号与系统sIgA18AS¥S1卫MS 〔例6.1.1):若x(n)的波形如图所示,求x(2n) x(n/2)的波形。 x2n 5 还应指出,对于离散信号压 缩后再展宽不能恢复原序列
〔例6.1.1〕:若x(n)的波形如图所示,求x(2n) x(n/2)的波形。 还应指出,对于离散信号压 缩后再展宽不能恢复原序列

·信号与系统SIGNAL84S1s1EM (5) 差分 (a)f(k)的后向差分,记 f(k)=f(c)-f(k-1) 又2f(对)=f(阳)-2f(k-1)+f(k-2) (b) f(k)的前向差分,记 Af(k)=fk+1)-f() Δ2f()=A[f(c)]=f(k+2)-2f(k+1)+f(k)
(5 (a)f(k)的后向差分,记 (b) f(k)的前向差分,记

·信号与系统SIGN AL8AS¥STEM 二、常用的离散时间信号 1. 单位序列 k=0 k0 性质:f(k)δ(k)=f(0)δ(k) f(k)(k-m)=f(m)(k-m) f(k)δ(k+m)=f(-m)δ(k+m)
二、常用的离散时间信号 1. 单位序列 = = 0 0 1 0 ( ) k k k (7-9) k 1 (k) 图 7 - 5 -1 0 1 性质: f (k) (k) = f (0) (k) f (k) (k − m) = f (m) (k − m) f (k) (k + m) = f (−m) (k + m)
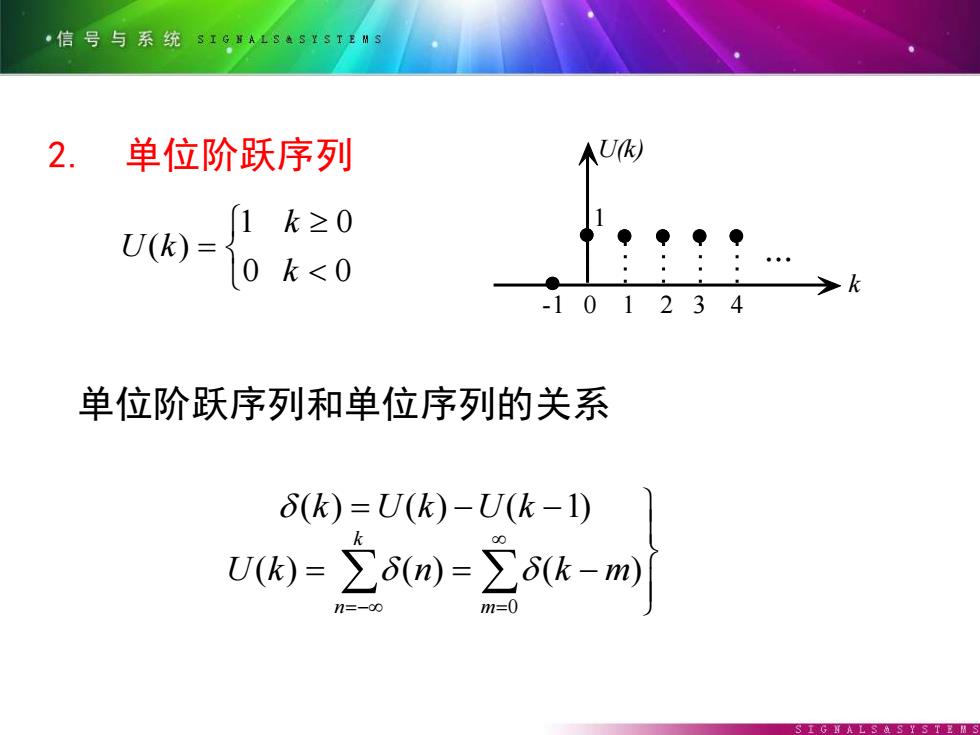
·信号与系统SIgA184S1s1EM 2. 单位阶跃序列 U k≥0 U()= 0 k<0 -101234 单位阶跃序列和单位序列的关系 6k)=U(k)-U(k-1) Uk)=立m)=∑k-m m=0
2. 单位阶跃序列 = 0 0 1 0 ( ) k k U k (7-10) k 1 U(k) 图 7 - 6 -1 0 1 2 3 4 = = − = − − =− =0 ( ) ( ) ( ) ( ) ( ) ( 1) m k n U k n k m k U k U k (7-11) 单位阶跃序列和单位序列的关系