
第五章 紫外-可见 一、普通分光光度法 分光光度法 二、示差分光光度法 三、双波长分光光度法 第四节 四、导数分光光度法 分光光度测定方法 下页 耀助 热回
第五章 紫外-可见 分光光度法 一、普通分光光度法 二、示差分光光度法 三、双波长分光光度法 第四节 四、导数分光光度法 分光光度测定方法
普通分光光度法 1.单组分的测定 通常采用A-C标准曲线法定量测定。 2.多组分的同时测定 A 组分a 组分b ()若各组分的吸收曲线互不重叠,则可 在各自最大吸收波长处分别进行测定。这 本质上与单组分测定没有区别。 入1 (2)若各组分的吸收曲线互有重叠,则可 根据吸光度的加合性求解联立方程组得出 各组分的含量。 Ax=Eamibca Ebxibcb 入2 432=8a2bca 8bx2bCb 上页 下页 返回
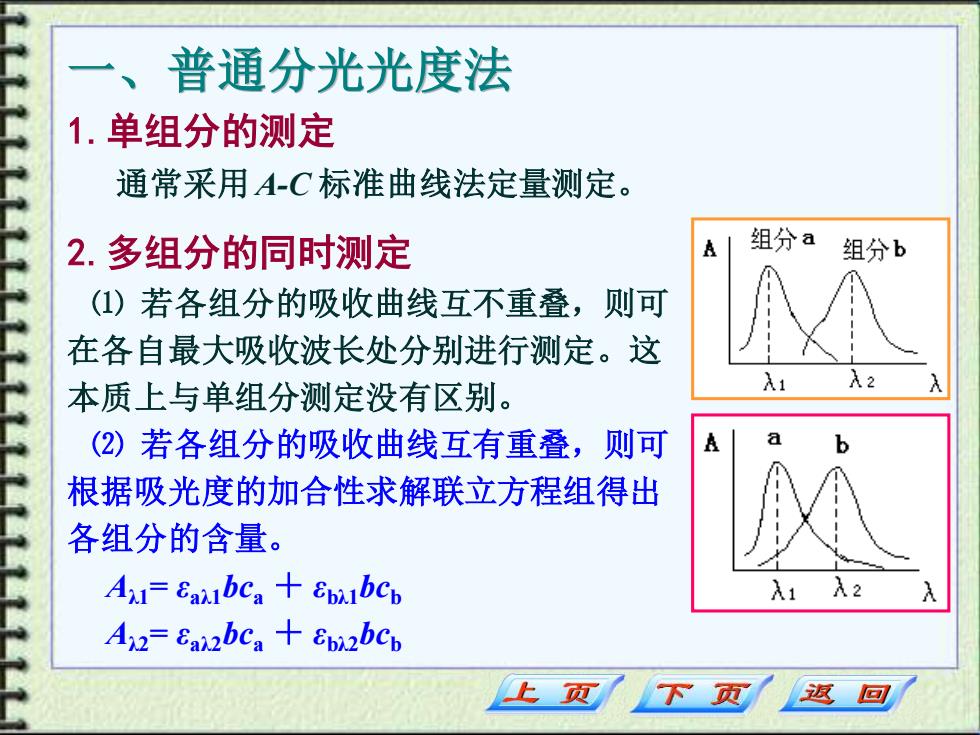
一、普通分光光度法 1.单组分的测定 通常采用 A-C 标准曲线法定量测定。 2.多组分的同时测定 ⑴ 若各组分的吸收曲线互不重叠,则可 在各自最大吸收波长处分别进行测定。这 本质上与单组分测定没有区别。 ⑵ 若各组分的吸收曲线互有重叠,则可 根据吸光度的加合性求解联立方程组得出 各组分的含量。 Aλ1= εaλ1bca + εbλ1bcb Aλ2= εaλ2bca + εbλ2bcb

二、示差分光光度法(示差法) 普通分光光度法一般只适于测定微量组分,当待测组分 含量较高时,将产生较大的误差。需采用示差法。即提高入 射光强度,并采用浓度稍低于待测溶液浓度的标准溶液作参 比溶液。 设:待测溶液浓度为c,标准溶液浓度为cs(c。〈C)。 则: Ax=Eb Cx As=&b Cs △A=Ax-A、=Eb(C、-C、)=b△c 测得的吸光度相当于普通法中待测溶液与标准溶液的吸 光度之差△A。 页 返 回
二、示差分光光度法(示差法) 普通分光光度法一般只适于测定微量组分,当待测组分 含量较高时,将产生较大的误差。需采用示差法。即提高入 射光强度,并采用浓度稍低于待测溶液浓度的标准溶液作参 比溶液。 设:待测溶液浓度为cx,标准溶液浓度为cs(cs < cx)。 则: Ax= εb cx As = εb cs ΔA=Ax -As =εb(cx - cs )=εbΔc 测得的吸光度相当于普通法中待测溶液与标准溶液的吸 光度之差ΔA

示差分光光度法(示差法) A=A-A、=b(C、-C、)=b△c 测得的吸光度相当于普通法中待测溶液与标准溶液的 吸光度之差A。 示差法测得的吸光度与△c呈直线关系。由标准曲线上 查得相应的△c值,则待测溶液浓度c: C=Cs+△c 上页下页了返回
示差分光光度法(示差法) ΔA=Ax -As =εb(cx - cs )=εbΔc 测得的吸光度相当于普通法中待测溶液与标准溶液的 吸光度之差ΔA。 示差法测得的吸光度与Δc呈直线关系。由标准曲线上 查得相应的Δc值,则待测溶液浓度cx : cx = cs + Δc
示差法标尺扩展原理: 普通法:c的T=10%;c的T=5% 示差法:c、做参比,调T=100% 则:c的T=50%;标尺扩展10倍 普通法 102030405060708090T% 示差法 102030405060708090T% 上页 下页 返回
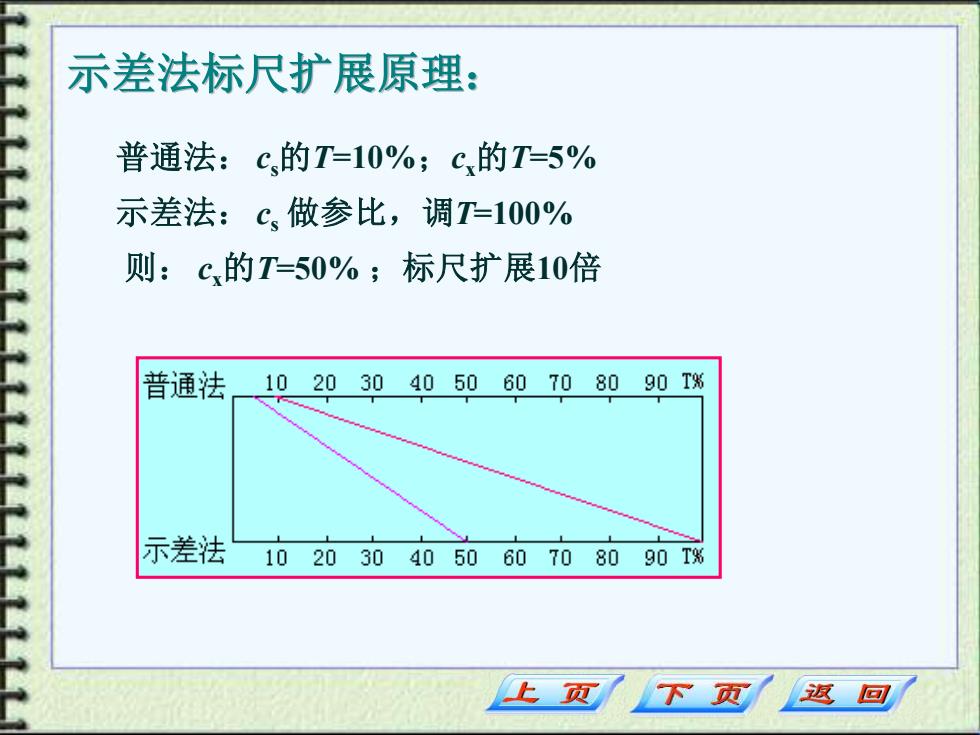
示差法标尺扩展原理: 普通法: cs的T=10%;cx的T=5% 示差法: cs 做参比,调T=100% 则: cx的T=50% ;标尺扩展10倍
三、双波长分光光度法 不需空白溶液作参比;但需要两个单色器获得两束单色 光(入1和入2);以参比波长九1处的吸光度Ax1作为参比,来 消除干扰。在分析浑浊或背景吸收较大的复杂试样时显示出 很大的优越性。灵敏度、选择性、测量精密度等方面都比单 波长法有所提高。 4A=Ax2-A1=(£x2-Ex1)bC 两波长处测得的吸光度差值A与待测组分浓度成正比 £x1和£λ2分别表示待测组分在入1和入2处的摩尔吸光系 数。 单色器 单色器 吸收池 接受器 双波长 下页 返回
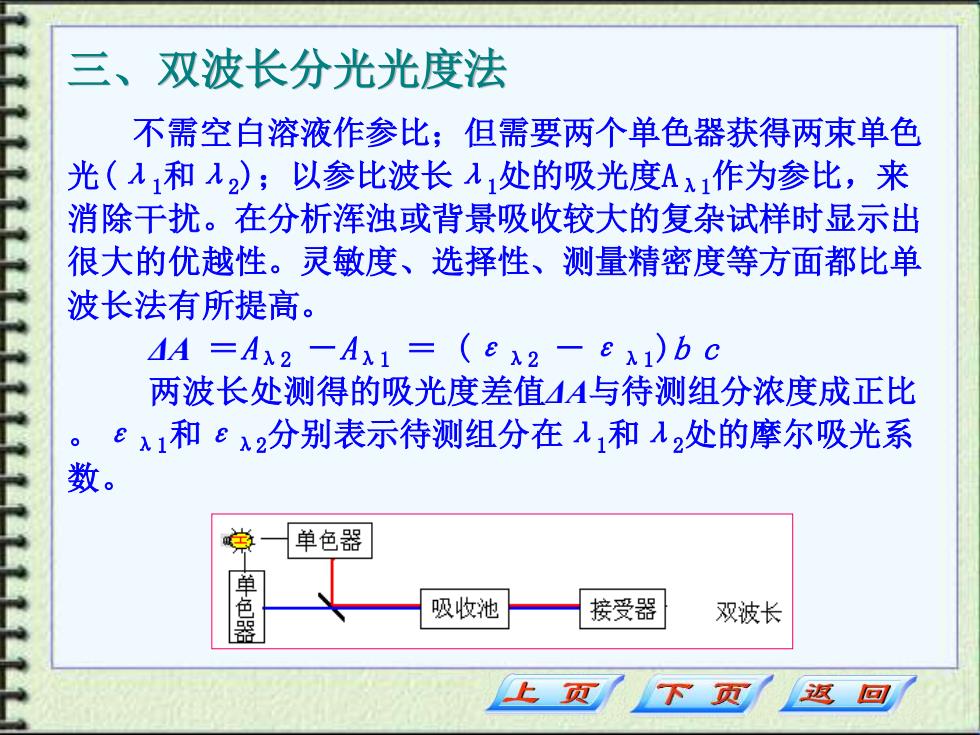
三、双波长分光光度法 不需空白溶液作参比;但需要两个单色器获得两束单色 光(λ1和λ2);以参比波长λ1处的吸光度Aλ1作为参比,来 消除干扰。在分析浑浊或背景吸收较大的复杂试样时显示出 很大的优越性。灵敏度、选择性、测量精密度等方面都比单 波长法有所提高。 ΔA =Aλ2 -Aλ1 = (ελ2 -ελ1)b c 两波长处测得的吸光度差值ΔA与待测组分浓度成正比 。ελ1和ελ2分别表示待测组分在λ1和λ2处的摩尔吸光系 数

关键问题: 测量波长入,和参比波长入,的选择与组合 以两组分x和的双波长法测定为例: 设:x为待测组分,为干扰组分,二者的吸光度差分别为: A,和A,则该体系的总吸光度差Ax+w为: AAxty=4Ax+4Ay 如何选择波长1、2有一定的要求。 单色器 单色器 吸收池 接受器 双波长 下页 返回
关键问题: 测量波长λ2和参比波长λ1的选择与组合 以两组分x和y的双波长法测定为例: 设:x为待测组分,y为干扰组分,二者的吸光度差分别为: ΔAx和ΔAy,则该体系的总吸光度差ΔAx+y为: ΔAx+y = ΔA x + ΔAy 如何选择波长λ1 、λ2有一定的要求
选择波长组合入1、入2的基本要求是: (1)选定的波长入和九,处干扰组分应具有相同吸光度, 即:Ay=Ayx2-Ayx1=0 故:Ax+y=Ax=(exx2-eXx1)bC 此时:测得的吸光度差A只与待测组分x的浓度呈线性关系 而与干扰组分y无关。若x为干扰组分,则也可用同样的方 法测定组分。 (2)在选定的两个波长入1 0.8 A 和入2处待测组分的吸光度应 0.; 具有足够大的差值。 可采用作图法选择符合 451 500 550 600 上述两个条件的波长组合。 A nm 返回
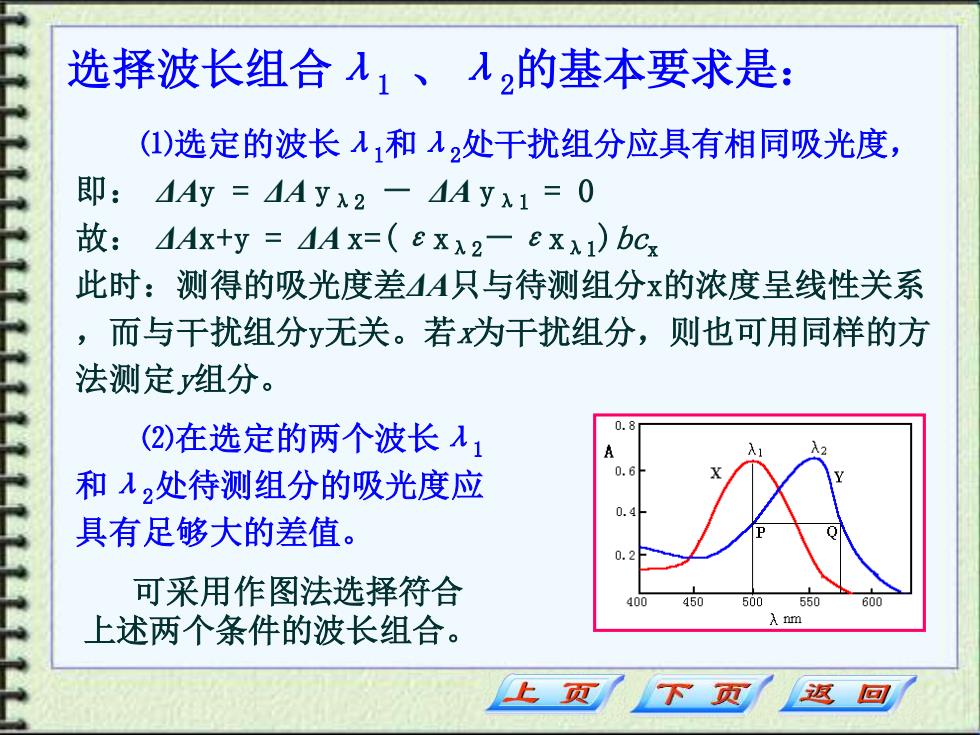
选择波长组合λ1 、λ2的基本要求是: ⑴选定的波长λ1和λ2处干扰组分应具有相同吸光度, 即: ΔAy = ΔA yλ2 - ΔA yλ1 = 0 故: ΔAx+y = ΔA x=(εxλ2-εxλ1)bcx 此时:测得的吸光度差ΔA只与待测组分x的浓度呈线性关系 ,而与干扰组分y无关。若x为干扰组分,则也可用同样的方 法测定y组分。 可采用作图法选择符合 上述两个条件的波长组合。 ⑵在选定的两个波长λ1 和λ2处待测组分的吸光度应 具有足够大的差值

四、导数分光光度法 导数分光光度法在多组分同时测定、浑浊样品分析、消 除背景干扰、加强光谱的精细结构以及复杂光谱的辨析等 方面,显示了很大的优越性。 利用吸光度(或透光度)对波长的导数曲线来进行分析: I=Ioe-e bc 假定入射光强度I。在整个波长范围内保持恒定: dI。/dx=0 则:dI/d入=-Io bc e-ebe d e/dX =-Io bc d s/da 下页 返回
四、导数分光光度法 导数分光光度法在多组分同时测定、浑浊样品分析、消 除背景干扰、加强光谱的精细结构以及复杂光谱的辨析等 方面,显示了很大的优越性。 利用吸光度(或透光度)对波长的导数曲线来进行分析: I=I0 e -εbc 假定入射光强度I0 在整个波长范围内保持恒定: dI 0 /dλ=0 则:dI/dλ=-I0 bc e -εbc dε/dλ =-I0 bc dε/dλ

导数分光光度法 dI/dλ=-Io bc de/d入 四阶导数光谱 一阶导数信号与试样浓度呈 线性关系; 三阶导数光谱 测定灵敏度依赖于摩尔吸光 系数对波长的变化率de/d。吸 二阶导数光谱 收曲线的拐点处de/dλ最大,故 其灵敏度最高(见图)。 一阶导数光谱 同理可以导出其二阶和三阶导 数光谱(略) 透光度曲线 上页 下页 返回
导数分光光度法 dI/dλ =-I0 bc dε/dλ 一阶导数信号与试样浓度呈 线性关系; 测定灵敏度依赖于摩尔吸光 系数对波长的变化率dε/dλ。吸 收曲线的拐点处dε/dλ最大,故 其灵敏度最高(见图)。 同理可以导出其二阶和三阶导 数光谱(略)