
第二章流体输送机械 流体输送机械:为流体提供外加能量的机械(机器√和设备)。 二、分类 泵,液体输送 按流体种类分 风机或压缩机或真空泵,气体输送 离心式 往复式 按原理分 旋转式 流体动力作用式
第二章 流体输送机械 一、流体输送机械:为流体提供外加能量的机械(机器和设备)。 二、分类 泵, 液体输送 按流体种类分 风机或压缩机或真空泵, 气体输送 离心式 往复式 按原理分 旋转式 流体动力作用式

第一节 液体输送机械 一、离心泵 1.结构:见图2-1。 2.原理:甩出、真空、吸入。 叶轮旋转时,叶片之间的液体随叶轮一起旋转,在离心力的作用下,液体沿叶片间的通道从叶 轮中心被甩到叶轮外围,具有很高的能量,从而液体可流到所需场所。 当液体被甩出后,在叶轮中心就会形成一定的真空,外界压力与该真空的压差就使液体经底 阀,吸入管道流入叶轮中心。这样,只要叶轮不停地旋转,液体就源源不断地被吸入和排出。 3.气缚:叶轮旋转时不能输送液体的现象。 若离心泵启动前未充满液体,则叶片间必充满气体。由于气体密度很小,所产生的离心力也 很小。所以在叶轮中心形成的真空不足以将液体吸入泵内,这时叶轮虽然旋转,但不能输送 液体。 4.主要部件 (1)叶轮:见图2-2和图23。 敞式(开式) 按叶片的形式分 半蔽式(半闭式) 蔽式(闭式) 单吸 按吸入方式分 双吸
第一节 液体输送机械 一、离心泵 1.结构:见图2-1。 2.原理:甩出、真空、吸入。 叶轮旋转时,叶片之间的液体随叶轮一起旋转,在离心力的作用下,液体沿叶片间的通道从叶 轮中心被甩到叶轮外围,具有很高的能量,从而液体可流到所需场所。 当液体被甩出后,在叶轮中心就会形成一定的真空,外界压力与该真空的压差就使液体经底 阀,吸入管道流入叶轮中心。这样,只要叶轮不停地旋转,液体就源源不断地被吸入和排出。 3.气缚:叶轮旋转时不能输送液体的现象。 若离心泵启动前未充满液体,则叶片间必充满气体。由于气体密度很小,所产生的离心力也 很小。所以在叶轮中心形成的真空不足以将液体吸入泵内,这时叶轮虽然旋转,但不能输送 液体。 4.主要部件 (1) 叶轮:见图2-2和图2-3。 敞式 (开式) 按叶片的形式分 半蔽式 (半闭式) 蔽式 (闭式) 单吸 按吸入方式分 双吸
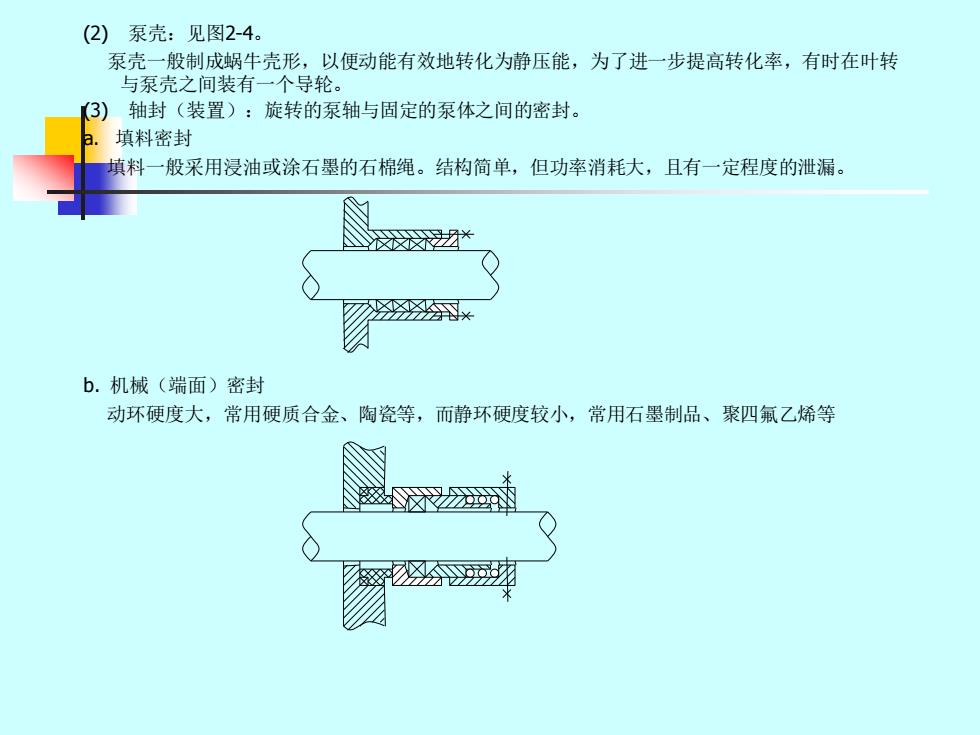
(2)泵壳:见图2-4。 泵壳一般制成蜗牛壳形,以便动能有效地转化为静压能,为了进一步提高转化率,有时在叶转 与泵壳之间装有一个导轮。 (3) 轴封(装置):旋转的泵轴与固定的泵体之间的密封。 填料密封 填料一般采用浸油或涂石墨的石棉绳。结构简单,但功率消耗大,且有一定程度的泄漏。 b.机械(端面)密封 动环硬度大,常用硬质合金、陶瓷等,而静环硬度较小,常用石墨制品、聚四氟乙烯等
(2) 泵壳:见图2-4。 泵壳一般制成蜗牛壳形,以便动能有效地转化为静压能,为了进一步提高转化率,有时在叶转 与泵壳之间装有一个导轮。 (3) 轴封(装置):旋转的泵轴与固定的泵体之间的密封。 a. 填料密封 填料一般采用浸油或涂石墨的石棉绳。结构简单,但功率消耗大,且有一定程度的泄漏。 b. 机械(端面)密封 动环硬度大,常用硬质合金、陶瓷等,而静环硬度较小,常用石墨制品、聚四氟乙烯等
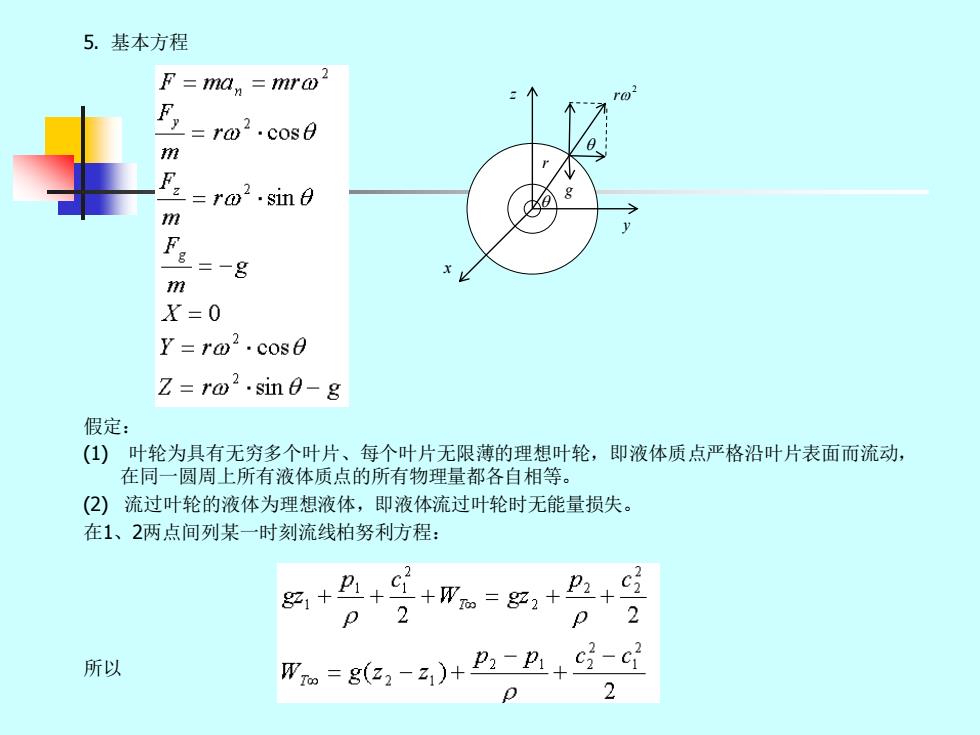
5.基本方程 F=ma,=mro2 ro F=ro.cos0 m =ro2.sin0 9 m 二一吕 m X=0 Y=ro2.cos0 Z ra2.sin0-g 假定: ()叶轮为具有无穷多个叶片、每个叶片无限薄的理想叶轮,即液体质点严格沿叶片表面而流动, 在同一圆周上所有液体质点的所有物理量都各自相等。 (2)流过叶轮的液体为理想液体,即液体流过叶轮时无能量损失。 在1、2两点间列某一时刻流线柏努利方程: +++。=,++ 所以 Wm=ga,-)+P,-+c号-c 2
5. 基本方程 假定: (1) 叶轮为具有无穷多个叶片、每个叶片无限薄的理想叶轮,即液体质点严格沿叶片表面而流动, 在同一圆周上所有液体质点的所有物理量都各自相等。 (2) 流过叶轮的液体为理想液体,即液体流过叶轮时无能量损失。 在1、2两点间列某一时刻流线柏努利方程: 所以 z x y g 2 r r

由流线柏努利方程的最初形式: Xk++Zt-1+1电d-h.床+h,+九)=d 2 对理想流体,有 xax+Ydy+zd-Idp+Id=d p at 2 对匀速离心力场和重力场中的稳定流动或某一时刻,有 ra'cos@ly+(ro'sin 0-g)d-dp-d 2 p 2 =0 wW+z02t-gt-1 p-d =0 2 对不可压缩流体沿流线进行不定积分,得 yo2+52-卫 =Const 2 2 p 2 r22 =Const 2 0 2 2-B 12 5o2 82- P2 好 P 2 2 2
由流线柏努利方程的最初形式: 对理想流体,有 对匀速离心力场和重力场中的稳定流动或某一时刻,有 对不可压缩流体沿流线进行不定积分,得

站在叶轮上,在1、2两点间列同一时刻流线柏努利方程,则 2g-4.w3@2 1 p22 82-2)+B-A=7o2-ra2 w2-w2 2 2 u-ui+wi-wi ((u=r@) 2 所以 -+w-w+-c 2 2 2 H-+-w+c- 2g 2g 2g 理论压头(2-4)(P87) 由余弦定理 w2=c2+42-2c41cosa% w=c号+4-2c4cosa2 =- 2C2c0SC2-41C1c0S1 得 8 基本方程(2-5)(P87)
站在叶轮上,在1、2两点间列同一时刻流线柏努利方程,则 所以 ——理论压头(2-4)(P87) 由余弦定理 得 ——基本方程(2-5)(P87)

在离心泵的设计中,一般使o1=90°,则c0s1=0 所以 42C2C0S2 8 cigp,=42-c cosa2 C,2 代入上式,得 uxC.acep 8 又将 er =Cy2nDb2 πD2n 42= 60 代入上式,得 = uetgBer π2Dn2 nctgB2Or gπDb2 3600g 60gb2 6.基本方程的讨论 (1)理论压头与叶轮直径及转速成正比。 (2)叶片的几何形状对理论压头的影响:
在离心泵的设计中,一般使1=90,则cos1=0 所以 将 代入上式,得 又将 代入上式,得 6.基本方程的讨论 (1) 理论压头与叶轮直径及转速成正比。 (2) 叶片的几何形状对理论压头的影响:

a.后弯叶片,B20, 8 径向叶片,B2=90°,ctg那2=0, =- 8 穹叶片,阝290°,Cg290°,Q↑,HT↑ b. B2=90°,Q↑,Hm→ C. B2<90°,Q个,H↓ H或 Qr或g 实际上,叶轮的叶片数是有限的,液体也是非理想液体,所以实际压头和实际流量的关系曲 线应在理论压头和理论流量的关系曲线的下方。 7.性能参数 (1)流量:单位时间内泵所输送的液体体积,Q,m/s、m/h或Ls。 (2)扬程(压头):单位重量的液体流经泵后所获得的能量,H,液柱。 扬程(一般)由实验测定,装置如图,原理如下:
a. 后弯叶片,290,ctg20, b. 径向叶片,2=90,ctg2=0, C. 前弯叶片,290,ctg20, 由上可见,2值越大,HT值越高,似乎前弯叶片较好。但由于2大于90以后,随2的增加, 动压头增加,静压头反而减小,从而能量损失大,效率低。因此,实际上离心泵的叶片总是 后弯的。 (3) 理论流量对理论压头的影响 当叶轮的几何尺寸(D2、b2、2 )和转速(n)一定时,理论压头与理论流量呈线性关系。 a. 290,QT,HT b. 2=90,QT,HT→ C. 2<90,QT,HT 实际上,叶轮的叶片数是有限的,液体也是非理想液体,所以实际压头和实际流量的关系曲 线应在理论压头和理论流量的关系曲线的下方。 7.性能参数 (1) 流量:单位时间内泵所输送的液体体积,Q,m3 /s、m3 /h或L/s。 (2) 扬程(压头):单位重量的液体流经泵后所获得的能量,H,m液柱。 扬程(一般)由实验测定,装置如图,原理如下: QT或Q HT或H
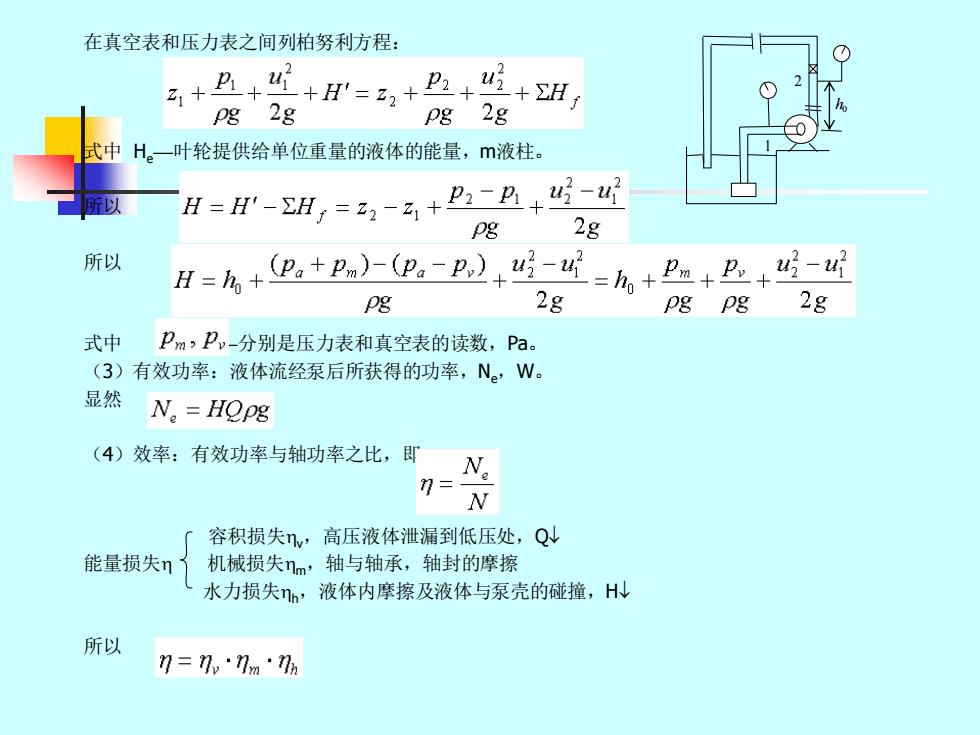
在真空表和压力表之间列柏努利方程: +A++=,+n++H, pg 2g pg 2g 式中H。一叶轮提供给单位重量的液体的能量,m液柱。 所以 H=H-H,=a2-a,+P:-B+5- pg 2g 所以 H=么+B,+P)m,-D)+5-4=h+P+L+ pg 2g pgpg 2g 式中 Pm,P,-分别是压力表和真空表的读数,Pa。 (3)有效功率:液体流经泵后所获得的功率,N。,W。 显然 N。=HQPg (4)效率:有效功率与轴功率之比,即 7= N 容积损失nw,高压液体泄漏到低压处,Q 能量损失n 机械损失nm,轴与轴承,轴封的摩擦 水力损失nh, 液体内摩擦及液体与泵壳的碰撞,HN 所以 7=7,·7m·7h
在真空表和压力表之间列柏努利方程: 式中 He—叶轮提供给单位重量的液体的能量,m液柱。 所以 所以 式中 ——分别是压力表和真空表的读数,Pa。 (3)有效功率:液体流经泵后所获得的功率,Ne,W。 显然 (4)效率:有效功率与轴功率之比,即 容积损失v,高压液体泄漏到低压处,Q 能量损失 机械损失m,轴与轴承,轴封的摩擦 水力损失h,液体内摩擦及液体与泵壳的碰撞,H 所以 1 2 h0
(5)轴功率:电机提供给泵轴的功率,N,W。 由 N。 7 得 N- HOpg 7 或 N=H10p×9.807xHgp 10007 1021 8.特性曲线:反应扬程、轴功率、效率和流量之间函数关系的曲线,一般用20°C的 清水在特定转速下由实验测定。由轴功率特性曲线知,启动泵时, n=2900rp min 应关闭出口阀门,以保护电机。 由效率特性曲线知,泵的工作点 应在高效率区(>92%)。 9.各因素对特性曲线的影响 (1)密度的影响 a.由泵的基本方程可知,扬程和流量均与液体的密度无关,所以HQ曲线不变。 b.由, N。_ HOpg 可知轴功率与密度成正比,否则轴功率不能与有效功率同步, 7= N N 所以效率也与密度无关,ηQ曲线不变。 C.由N= HOP 知,NwQ曲线有变。 1027
(5)轴功率:电机提供给泵轴的功率,N,W。 由 得 或 8. 特性曲线:反应扬程、轴功率、效率和流量之间函数关系的曲线,一般用20C的 清水在特定转速下由实验测定。由轴功率特性曲线知,启动泵时, 应关闭出口阀门,以保护电机。 由效率特性曲线知,泵的工作点 应在高效率区(92%)。 9.各因素对特性曲线的影响 (1) 密度的影响 a. 由泵的基本方程可知,扬程和流量均与液体的密度无关,所以H~Q曲线不变。 b. 由, 可知轴功率与密度成正比,否则轴功率不能与有效功率同步, 所以效率也与密度无关,~Q曲线不变。 C. 由 知,N~Q曲线有变。 H N n = 2900rp min