
第二章 半导体中的结理论 第一节号 异质结及其能带图 一、基本概念 ●同质结(Homo junct ion):禁带宽度相同但因掺杂型号 不同或虽型号相同但掺杂浓度不同组成晶体界面。 如:n-GaAs/p-GaAs,n-GaAs/nt-GaAs ●异质结(Heterojunct ion):由两种禁带宽不同的单晶 材料组成的晶体界面。 如:A/xGa1-xAs/GaAs,GexS11-xSi 材料1:Eg,材料2:Eg2Eg1丰Eg2
第一节 异质结及其能带图 一、基本概念 第二章 半导体中的结理论 ⚫同质结 (Homojunction):禁带宽度相同但因掺杂型号 不同或虽型号相同但掺杂浓度不同组成晶体界面。 如:n-GaAs/p-GaAs, n-GaAs/n + -GaAs ⚫异质结 (Heterojunction): 由两种禁带宽不同的单晶 材料组成的晶体界面。 如: AlxGa1-xAs/GaAs, GexSi1-x/Si 材料1:Eg1,材料2:Eg2, Eg1 ≠ Eg2

异质结的概念 突变结:在异质结界面附近,两种材料的组分 、掺杂浓度发生突变,有明显的空间电荷区边 界,其厚度仅为若干原子间距。 缓变结:在异质结界面附近,组分和掺杂浓度 逐渐变化,存在有一过渡层,其空间电荷浓度 也逐渐向体内变化,厚度可达几个电子或空穴 的扩散长度
异质结的概念 ⚫突变结:在异质结界面附近,两种材料的组分 、掺杂浓度发生突变,有明显的空间电荷区边 界,其厚度仅为若干原子间距。 ⚫缓变结:在异质结界面附近,组分和掺杂浓度 逐渐变化,存在有一过渡层,其空间电荷浓度 也逐渐向体内变化,厚度可达几个电子或空穴 的扩散长度

网 异质结的概念 ● 同型异质结:导电类型相同的异质结 如:N-Al Ga1-xAsn-GaAs, p-Ge Si1/p-Si ● 异型异质结:导电类型不同的异质结 如:N-A/xGa1-xAs/p-GaAs, p-Ge Si1-n-Si
异质结的概念 ⚫ 同型异质结:导电类型相同的异质结 如:N-AlxGa1-xAs/n-GaAs, p-GexSi1-x/p-Si ⚫ 异型异质结:导电类型不同的异质结 如:N-AlxGa1-xAs/p-GaAs, p-GexSi1-x/n-Si
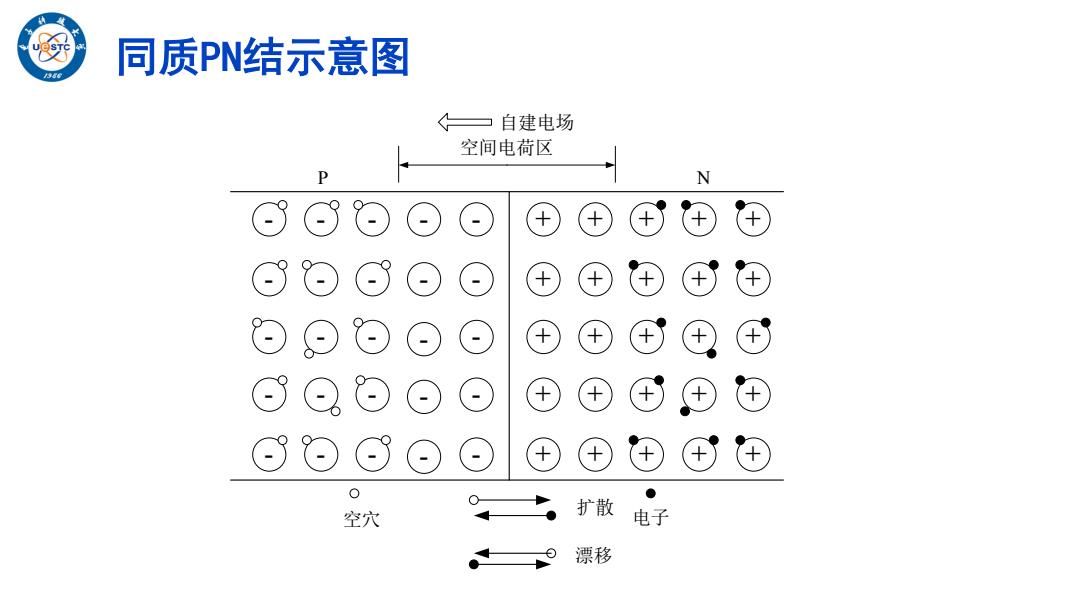
同质PN结示意图 《一自建电场 空间电荷区 P N 、 Q 、P 0 空穴 扩散 电子 漂移
- - - - - - - - - - - - - - - - - - - - - - - - - + + + + + + + + + + + + + + + + + + + + + + + + + P N 空间电荷区 自建电场 空穴 电子 扩散 漂移 同质PN结示意图
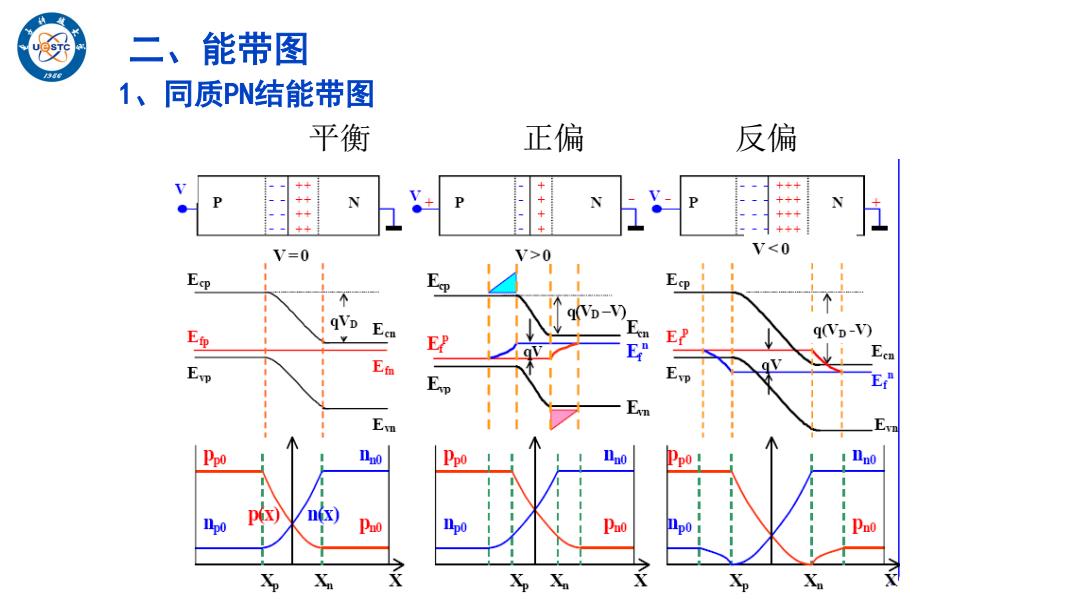
二、能带图 1、同质PN结能带图 平衡 正偏 反偏 ++ ++ V=0 7>0 T<0 个 个 qVD q(Vp-V) EP av p E Ppo p0 Pno X Xp
平衡 正偏 反偏 1、同质PN结能带图 二、能带图

导带底电子、价带底空穴 A=yep-K) 风=Nm气 R=NegB KT )=Nm
0 exp( ) c F c B E E n N K T − = − 0 exp( ) F v v B E E p N K T − = − exp( ) n c F c B E E n N K T − = − exp( ) p F v v B E E p N K T − = − 导带底电子、价带底空穴

2、异质结能带图确定方法 安德森(Ander son)能带模型 假定: 1、在异质结界面处不存在界面态和偶极态; 2、异质结界面两边的空间电荷层(或耗尽层中),空间电 荷 的符号相反、大小相等; 3、异质结界面两边的介电常数分别为c,和c2,c12,界面处 的电场不连续: 81E1-82E2 E1≠E20
2、异质结能带图确定方法 安德森(Anderson)能带模型 假定: 1、在异质结界面处不存在界面态和偶极态; 2、异质结界面两边的空间电荷层(或耗尽层中),空间电 荷 的符号相反、大小相等; 3、异质结界面两边的介电常数分别为1和2 ,1 2 ,界面处 的电场不连续: 1 E1 =2 E2 E1 E2
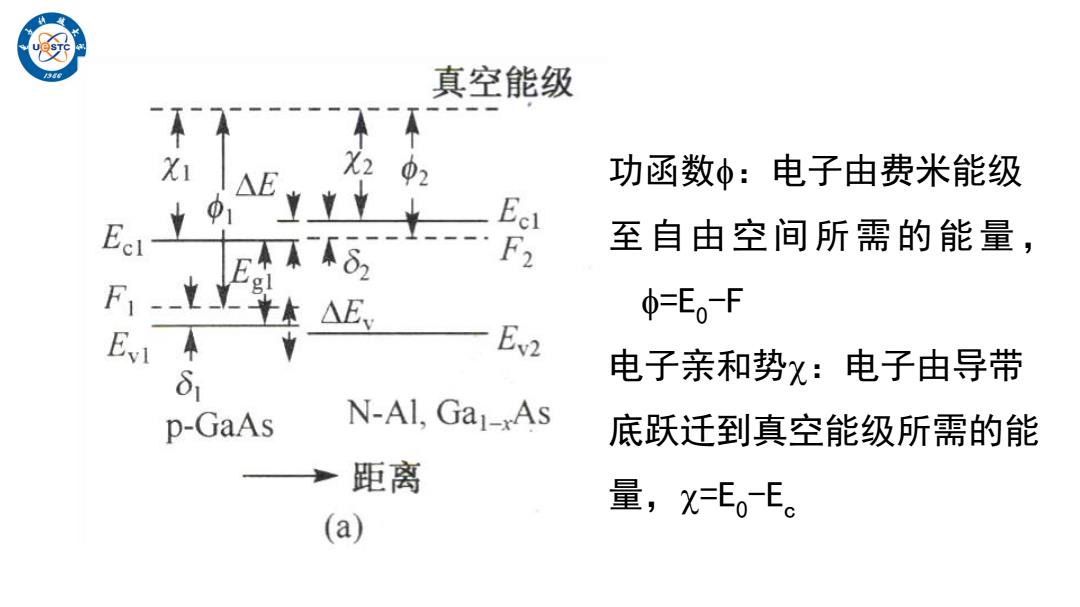
真空能级 △E 02 功函数中:电子由费米能级 01 E不 F2 至自由空间所需的能量, F-t △E, Φ=E0F Ev2 δ1 电子亲和势%:电子由导带 p-GaAs N-Al,Ga_As 底跃迁到真空能级所需的能 →距离 量,X=E。E。 (a)
功函数:电子由费米能级 至自由空间所需的能量, =E0 -F 电子亲和势:电子由导带 底跃迁到真空能级所需的能 量,=E0 -E c
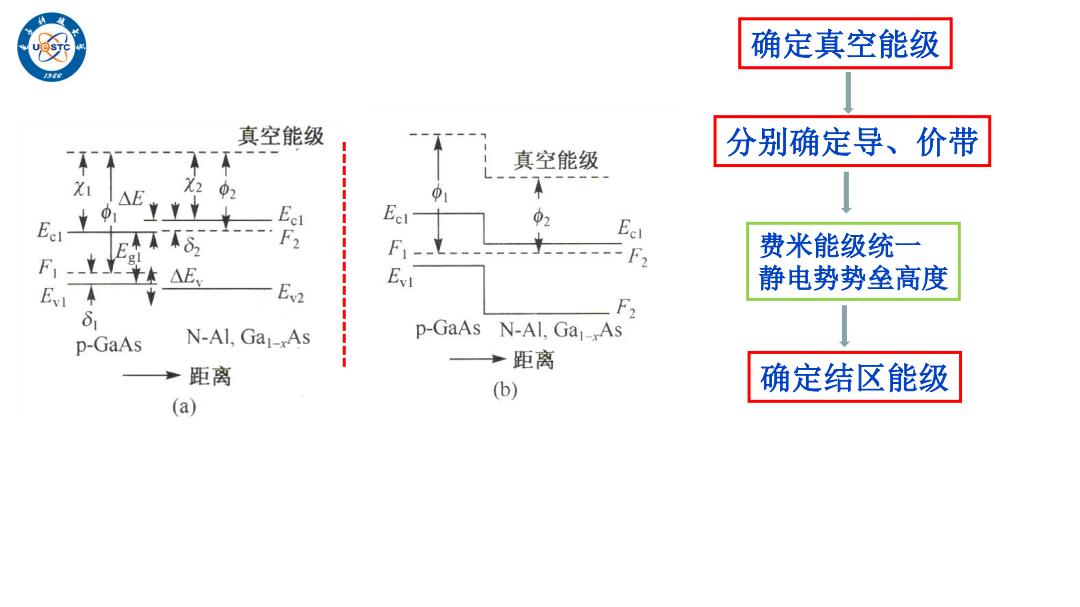
确定真空能级 真空能级 分别确定导、价带 真空能级 X I△E X2 0 02 F 费米能级统一 F1- ---F2 △E Ev2 静电势势垒高度 F δ1 N-Al,Ga-As p-GaAs N-Al,GaAs p-GaAs →距离 距离 (b) 确定结区能级 (a)
确定真空能级 分别确定导、价带 费米能级统一 静电势势垒高度 确定结区能级
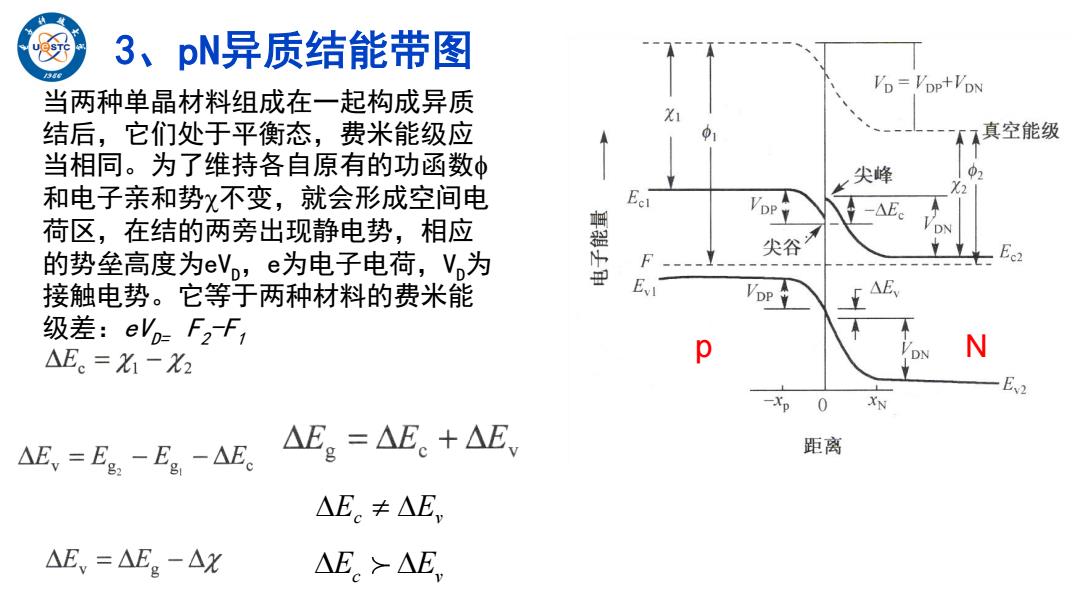
3、pN异质结能带图 VD=VDP+VDN 当两种单晶材料组成在一起构成异质 结后,它们处于平衡态,费米能级应 真空能级 当相同。为了维持各自原有的功函数中 尖峰 和电子亲和势不变,就会形成空间电 -△E 荷区,在结的两旁出现静电势,相应 的势垒高度为eV,e为电子电荷,V,为 尖谷 接触电势。它等于两种材料的费米能 △E 级差:eV,F2f) △E。=X-X2 D N 0 XN AE,=E-E。-△E。 △Eg=△E。+△E 距离 △E。≠△E, △E,=△Eg-△X △E,>AE
3 、pN异质结能带图 p N 当两种单晶材料组成在一起构成异质 结后 ,它们处于平衡态 ,费米能级应 当相同 。为了维持各自原有的功函数 和电子亲和势 不变 ,就会形成空间电 荷区 ,在结的两旁出现静电势 ,相应 的势垒高度为eV D , e为电子电荷 , V D 为 接触电势 。它等于两种材料的费米能 级差:eVD= F2 -F1 E E c v E E c v