
狭义相对论 Xidian University 本章内容(Special Relativity) §1狭义相对论的实验基础 §2狭义相对论的基本原理 洛仑兹变换 §3狭义相对论的时空理论 §4狭义相对论动力学简介 §5狭义相对论理论的四维形式 §6电动力学的相对论不变性 西安电子科技大学
西安电子科技大学 2 §1 狭义相对论的实验基础 本章内容 §2 狭义相对论的基本原理 洛仑兹变换 §3 狭义相对论的时空理论 §4 狭义相对论动力学简介 §5 狭义相对论理论的四维形式 §6 电动力学的相对论不变性 (Special Relativity) 狭义相对论

狭义相对论 Xidian University §1狭义相对论的实验基础 引言 牛顿力学 ·19世纪后期,经典物理学 的三大理论体系使经典物理 麦克斯韦电磁场理论 学已趋于成熟。 热力学与经典统计理论 “在已经基本建成的科学大厦中,后辈的 物理学家只要做一些零碎的修补工作就行了。 “但是,在物理学晴朗天空的远处,还有 两朵令人不安的乌云” 开尔文 狭义相对论 量子力学 近代物理不是对经典理论的简单否定 近代物理不是经典理论的补充,而是全新的理论甲 西安电子科技大学
西安电子科技大学 §1 狭义相对论的实验基础 引言 牛顿力学 麦克斯韦电磁场理论 热力学与经典统计理论 • 19世纪后期,经典物理学 的三大理论体系使经典物理 学已趋于成熟。 “在已经基本建成的科学大厦中,后辈的 物理学家只要做一些零碎的修补工作就行了。” “但是,在物理学晴朗天空的远处,还有 两朵令人不安的乌云” 狭义相对论 量子力学 • 近代物理不是对经典理论的简单否定 • 近代物理不是经典理论的补充,而是全新的理论 狭义相对论
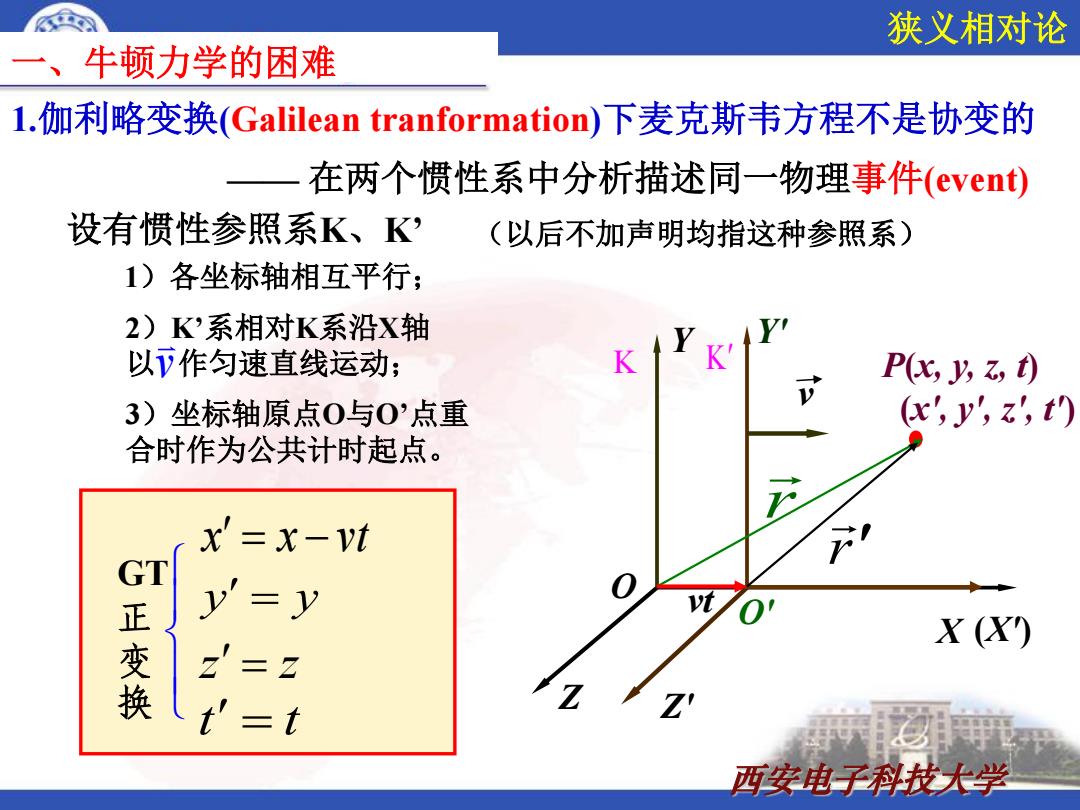
狭义相对论 一、牛顿力学的困难 l.伽利略变换(Galilean tranformation)下麦克斯韦方程不是协变的 在两个惯性系中分析描述同一物理事件(event) 设有惯性参照系K、K, (以后不加声明均指这种参照系) 1)各坐标轴相互平行; 2)K?系相对K系沿X轴 以下作匀速直线运动; K P化,J,t) 3)坐标轴原点0与0'点重 (x,y,,t) 合时作为公共计时起点。 x'=x-vt GT 正 -y X(X 变换 z'=z =t 西安电子科技大学
西安电子科技大学 GT 正 变 换 x x vt y y z z t t —— 在两个惯性系中分析描述同一物理事件(event) 1.伽利略变换(Galilean tranformation)下麦克斯韦方程不是协变的 O Z X Y O' Z' (X') Y' v P(x, y, z, t) r r K K Z (x′, y′, z′, t′) 一、牛顿力学的困难 设有惯性参照系K、K’ 3)坐标轴原点O与O’点重 合时作为公共计时起点。 1)各坐标轴相互平行; 2)K’系相对K系沿X轴 以 v 作匀速直线运动; (以后不加声明均指这种参照系) vt 狭义相对论
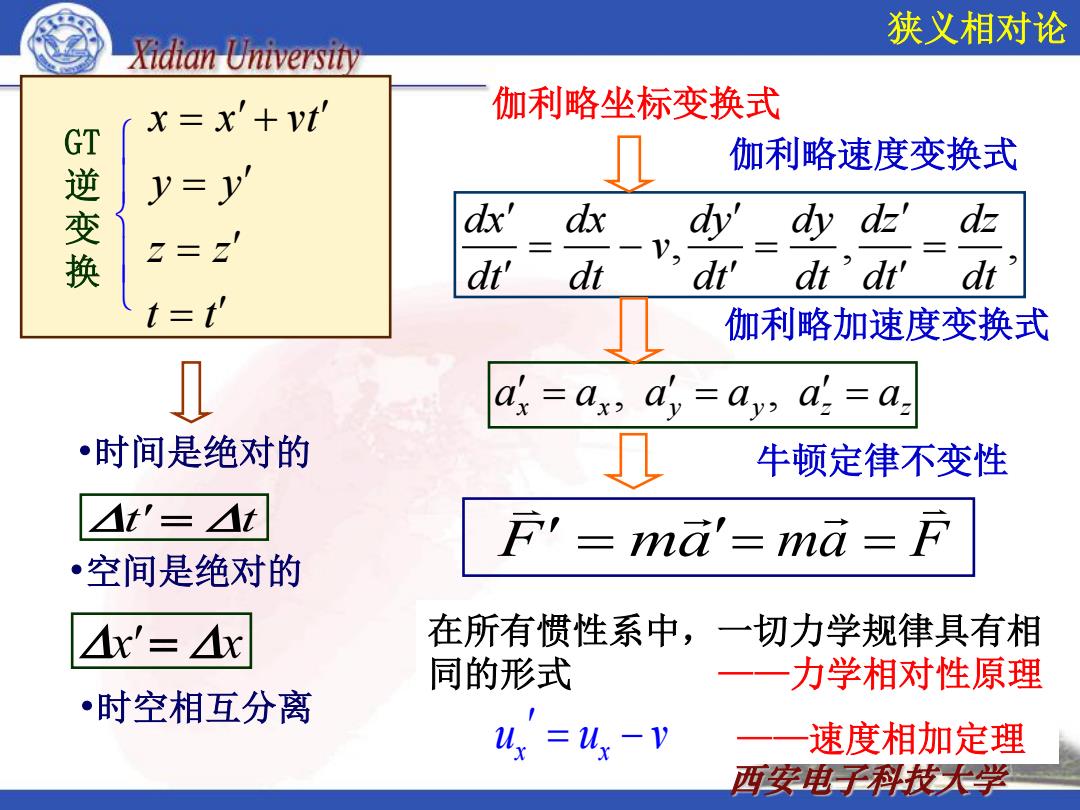
狭义相对论 Xidian Universin x=x'+vt 伽利略坐标变换式 伽利略速度变换式 逆变换 y=y' dx' dx dy'dy dz'dz 2=2' dt' dt dt' dt'dr dt =t' 伽利略加速度变换式 as as,ay ay,a'a: •时间是绝对的 牛顿定律不变性 △t'=At F'ma'=ma =F 空间是绝对的 Ax'=Ax 在所有惯性系中,一切力学规律具有相 同的形式 力学相对性原理 •时空相互分离 ux =ux-v 速度相加定理 西安电子科技大学
西安电子科技大学 GT 逆 变 换 , , , dx dx dy dy dz dz v dt dt dt dt dt dt 伽利略坐标变换式 伽利略速度变换式 , , x x y y z z a a a a a a 伽利略加速度变换式 牛顿定律不变性 F ma ma F •时间是绝对的 •空间是绝对的 t' t x' x •时空相互分离 x x vt y y z z t t 在所有惯性系中,一切力学规律具有相 同的形式 ——力学相对性原理 u u v x x ——速度相加定理 狭义相对论

狭义相对论 Xidian University 问题:Maxwel1电磁理论是否也满足相对性原理? 据绝对时空理论,答案是否定的 据绝对时空理论。光速依赖于惯性系 真空中的光速等于c仅对某一特殊的绝对静止惯性系才成立 因此Maxwel1方程组也只能对该特殊参考系成立。 2.速度合成律应用于光传播时的矛盾 光传到乙的时间:△t=l/c 光传到乙的时间:△t2=/(c+v) ∴.△t2<△t1先出球,后击球 -因果先后颠倒 西安电子科技大学
西安电子科技大学 v 2.速度合成律应用于光传播时的矛盾 2 1 t t 先出球,后击球 ----因果先后颠倒 2 光传到乙的时间: t l c v ( ) 光传到乙的时间: 1 t l c 乙 甲 问题:Maxwell电磁理论是否也满足相对性原理? 据绝对时空理论,答案是否定的 据绝对时空理论。光速依赖于惯性系 真空中的光速等于c仅对某一特殊的绝对静止惯性系才成立 ,因此Maxwell方程组也只能对该特殊参考系成立。 狭义相对论

狭义相对论 Xidian University 3.迈克尔逊-莫雷(Michelson-Morley)实验证明以太不存在 ·假定在“以太”(ether)中光速各向同性且恒等于C,而在其它 参考系光速各向异性。 ·假定太阳与以太固连,地球相对于以太的速度就应当是地球 绕太阳的运动速度。 M, 对光线(1):O→M,>O 6=1+1-2 11 C+v c-v 1-v2/c2 M 地球系 以太风 西安电子科技大学
西安电子科技大学 P M1 M2 2 l 1 l v O •假定在“以太”(ether)中光速各向同性且恒等于C,而在其它 参考系 光速各向异性。 •假定太阳与以太固连,地球相对于以太的速度就应当是地球 绕太阳的运动速度。 1 1 1 l l t c v c v 1 2 2 2 1 1 / l c v c 对光线(1) : O M1 O 地球系 v 以太风 3.迈克尔逊-莫雷(Michelson-Morley)实验证明以太不存在 狭义相对论

狭义相对论 Xidian University 对光线(2) M,M, 0→M,→O 巧=2 ve2-v2 调节41=1=1 21 21 △t=t2-t1= a1-)=cw 仪器转动π/2 21 21 △t'=t2-t= D< 引起干涉条 纹的移动: 光程差 a6=-⊙≈215 21y2 AN= 1c2 光程差与条纹移动关系△δ=△N几 西安电子科技大学
西安电子科技大学 M2 G 对光线(2) O M2 O 2 2 2 2 2 l t c v 调节 1 2 l l l (1 ) 2 (1 ) 2 2 2 2 1 2 2 1 2 c v c l c v c l t t t (v c) 2 2 1 2 2 v l c 光程差 光程差与条纹移动关系 N 仪器转动 / 2 2 1 2 2 2 2 1 2 (1 ) 2 (1 ) 2 c v c l c v c l t t t 2 c t 1 c t 引起干涉条 纹的移动: 2 2 c 2l v N M2 G c G v 2 2 c v 狭义相对论

狭义相对论 Xidian University §2 狭义相对论的基本原理 洛仑兹变换 一、狭义相对论的两个基本假设 (1905年,A.Einstein) l.光速不变原理(Einstein's Principle of Constant Speed of Light) 在所有的惯性系中,光在真空中的传播速率为C。 c=299792458m/s 说明 。光速与观察者的参考系无关,不随观察者的 运动而变化;光速与光源的运动状态也无关 2.狭义相对论的相对性原理 (Einstein's Principle of Relativity) >一切物理规律在所有惯性系中具有相同的形式 >所有惯性系都完全处于平权的,没有任何理由选 某一个参考系并把它置于特殊的地位。 西安电子科技大学
西安电子科技大学 (1905年,A.Einstein) 299 792 458 m/s c 1. 光速不变原理(Einstein’s Principle of Constant Speed of Light) 在所有的惯性系中,光在真空中的传播速率为 C 。 说明 • 光速与观察者的参考系无关,不随观察者的 运动而变化 ;光速与光源的运动状态也无关 所有惯性系都完全处于平权的,没有任何理由选 某一个参考系并把它置于特殊的地位。 一、狭义相对论的两个基本假设 2. 狭义相对论的相对性原理 一切物理规律在所有惯性系中具有相同的形式 §2 狭义相对论的基本原理 洛仑兹变换 狭义相对论 (Einstein’s Principle of Relativity)

狭义相对论 Xidian University 二、洛仑兹变换(Lorentz transformation) P.(x',y',z',t') 对新变换的要求: (x,y,z,t) 1)线性 2)新变换在低速下应满足GT X >间隔不变性 两事件(x1,1,),(x2y2,242) 的间隔为 (K系)s2=c2(-4)-(x2-x)2-(2-y)2-(32-)月 (x1,),(x5y5,2,)的间隔为 (K”系)s2=2(G-)2-(x-x)-(-0)2-(5-) 间隔不变性即 s2=s2 西安电子科技大学
西安电子科技大学 二、洛仑兹变换(Lorentz transformation) X Z Y O Z’ X’ Y’ O’ P: x y z t ', ', ', ' x y z t , , , v 对新变换的要求: 1)线性 2)新变换在低速下应满足GT 狭义相对论 间隔不变性 两事件 x y z t x y z t 1 1 1 1 2 2 2 2 , , , , , , , 的间隔为 2 2 2 2 2 2 2 1 2 1 2 1 2 1 (K系) s c t t x x y y z z (K’系) x y z t x y z t 1 1 1 1 2 2 2 2 , , , , , , , 的间隔为 2 2 2 2 2 2 2 1 2 1 2 1 2 1 s c t t x x y y z z 间隔不变性即 2 2 s s

狭义相对论 Xidian University >洛仑兹变换(LT)的推导 设x'=a11x+a12t dx 当x'=0时 =v V=- 12 d 11 y'=y 当x=0时 12 z'=2 dt' a22 t'=a21X+a22 又s2=s2 c2-x2-y0-z0=c-x2-y2-z3 c'(azx tax)-ax ad )2y22122* 2号2 比较对应项系数,可得 a-c'a =1 -V /c2 caia-h-v 西安电子科技大学
西安电子科技大学 当 x 0 dx v dt 时 12 11 a v a 12 22 a v a 11 22 a a 当 x ' 0 dx v dt 时 11 12 21 22 ' ' ' ' x a x a t y y z z t a x a t 设 洛仑兹变换(LT)的推导 狭义相对论 又 2 2 2 2 2 22 2 2 2 ct x y z ct x y z 2 2 s s 2 2 2 2 2 22 2 2 2 21 22 11 12 c ax at ax at y z ct x y z ( ) ( ) 比较对应项系数,可得 2 12 21 a c a 11 21 2 2 2 a c a 1 11 12 2 2 2 2 c a a c 11 22 2 2 1 , 1 a a v c 12 2 2 , 1 v a v c 2 21 2 2 1 v c a v c