
振动理论与声学原理 4 1956 第二章单自由度系统的自由振动 牛顿(1643年1月4日一1727年3月31日)是一 位英国物理学家、数学家、剑桥大学数学教授 英国皇家学会主席。他在1687年发表的论文 《自然哲学与数学原理》里,对万有引力和三 大运动定律进行了描述。这些描述奠定了此后 三个世纪里物理世界的科学观点,并成为了现 代工程学的基础
1 第二章 单自由度系统的自由振动 牛顿(1643年1月4日—1727年3月31日)

课堂讨论主题2: 口主题:单自由度系统振动案例分析 口时间:9月27日(10-11节课) 口各小组从提供的8个案例中选取一个案例进行分析; 并通过文献查阅说明其工程应用场景。 口课堂PPT交流与讨论,每组15分钟。 3
课堂讨论主题2: 3 p 主题:单自由度系统振动案例分析 p 时间:9月27日(10-11节课) p 各小组从提供的8个案例中选取一个案例进行分析; 并通过文献查阅说明其工程应用场景。 p 课堂PPT交流与讨论,每组15分钟
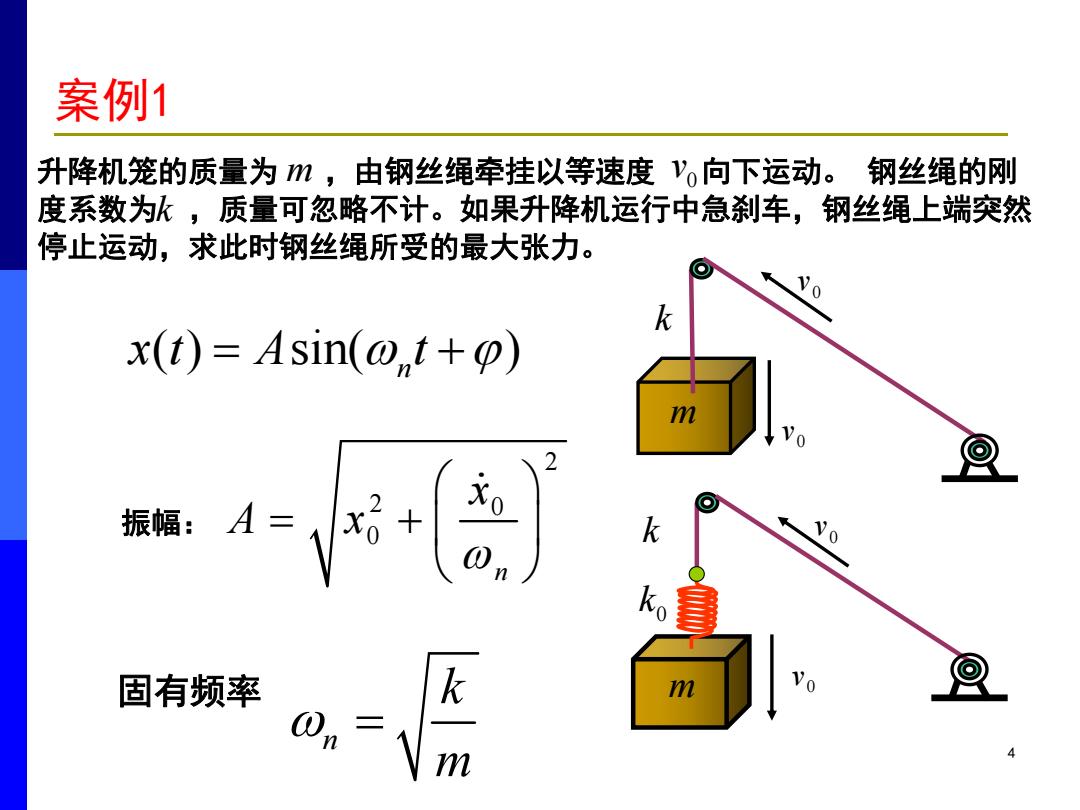
案例1 升降机笼的质量为m,由钢丝绳牵挂以等速度'o向下运动。钢丝绳的刚 度系数为k,质量可忽略不计。如果升降机运行中急刹车,钢丝绳上端突然 停止运动,求此时钢丝绳所受的最大张力。 k x(t)=Asin(@,t+) m V 振幅:A= 固有频率 k m (n m
4 升降机笼的质量为 ,由钢丝绳牵挂以等速度 向下运动。 钢丝绳的刚 度系数为 ,质量可忽略不计。如果升降机运行中急刹车,钢丝绳上端突然 停止运动,求此时钢丝绳所受的最大张力。 m 0 v k 0 v 0 v m k 0 m v k 0 k 0 v 案例1 ( ) sin( ) n x t A t 振幅: 2 2 0 0 n x A x n k m 固有频率

案例2 提升机系统。重物W仁1.47x105N,钢丝刚度k=5.78x104W/cm。重物以 v=15m/min的速度匀速下降,求绳的上端突然卡住时, (1) 重物的振动频率;(2)绳中最大张力。 x(t)=Asin(@,t+) W 初相位:p=arctan k 固有频率 0n= 5
5 提升机系统。重物W=1.47x105N,钢丝刚度k=5.78x104N/cm。重物以 v=15m/min的速度匀速下降,求绳的上端突然卡住时, (1)重物的振动频率;(2)绳中最大张力。 ( ) sin( ) n x t A t 振幅: 2 2 0 0 n x A x n k m 固有频率 0 0 arctan n x x 初相位: 案例2
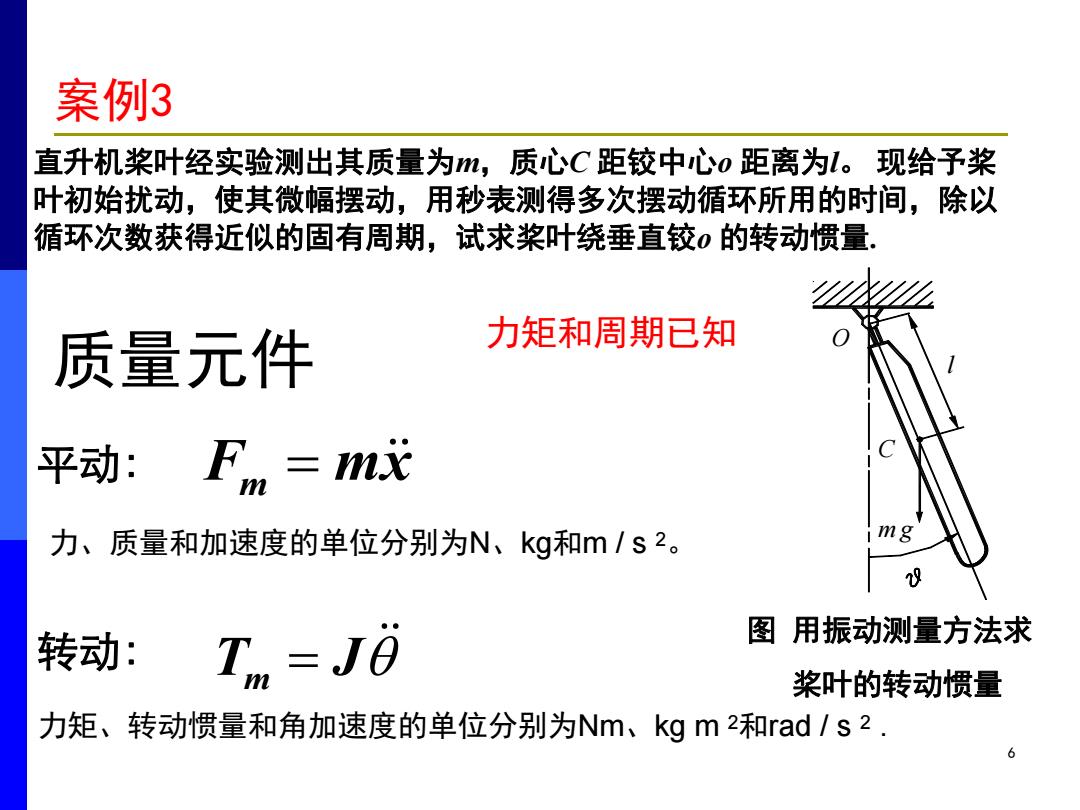
案例3 直升机桨叶经实验测出其质量为m,质心C距铰中心o距离为l。现给予桨 叶初始扰动,使其微幅摆动,用秒表测得多次摆动循环所用的时间,除以 循环次数获得近似的固有周期,试求桨叶绕垂直铰o的转动惯量. 质量元件 力矩和周期已知 平动:Fm=m成 力、质量和加速度的单位分别为N、kg和m/s2。 转动: T=J0 图用振动测量方法求 桨叶的转动惯量 力矩、转动惯量和角加速度的单位分别为Nm、kgm2和rad/s2
6 O l C m g 直升机桨叶经实验测出其质量为m,质心C 距铰中心o 距离为l。 现给予桨 叶初始扰动,使其微幅摆动,用秒表测得多次摆动循环所用的时间,除以 循环次数获得近似的固有周期,试求桨叶绕垂直铰o 的转动惯量. 图 用振动测量方法求 桨叶的转动惯量 质量元件 Tm J 转动: 平动: Fm mx 力、质量和加速度的单位分别为N、kg和m / s 2 。 力矩、转动惯量和角加速度的单位分别为Nm、kg m 2和rad / s 2 . 力矩和周期已知 案例3
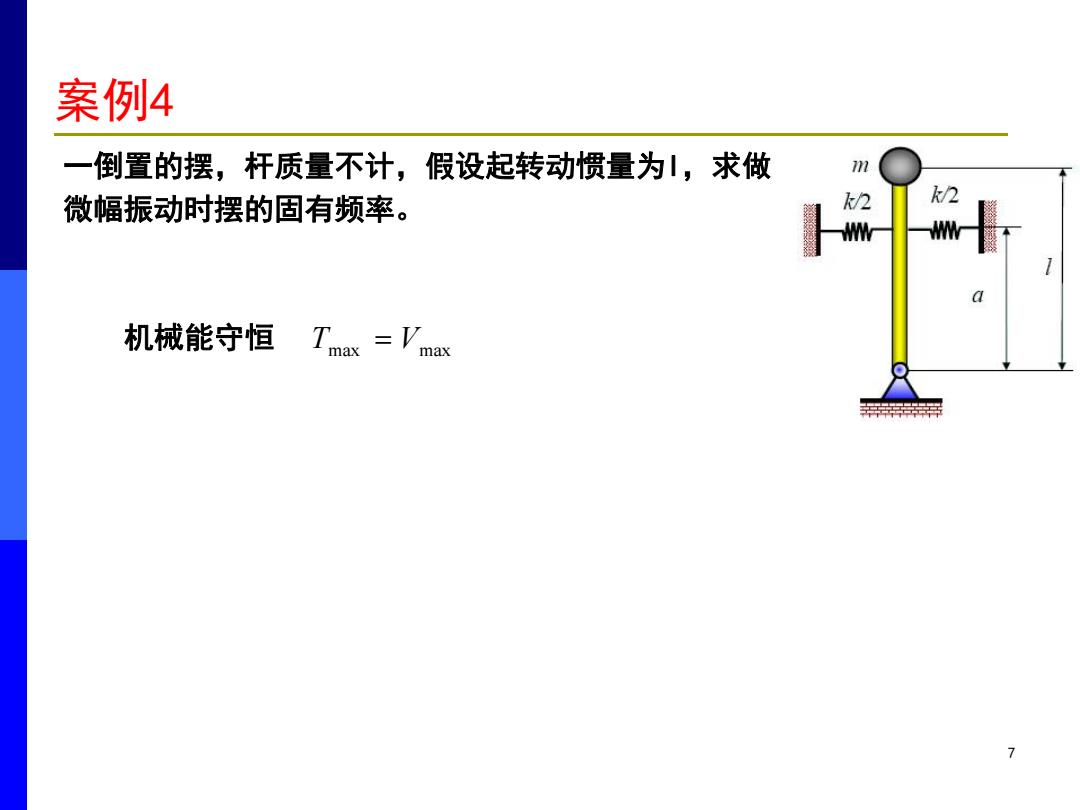
案例4 一倒置的摆,杆质量不计,假设起转动惯量为,求做 m 微幅振动时摆的固有频率。 2 k/2 机械能守恒 T'max =V max 7
7 一倒置的摆,杆质量不计,假设起转动惯量为I,求做 微幅振动时摆的固有频率。 机械能守恒 Tmax Vmax 案例4
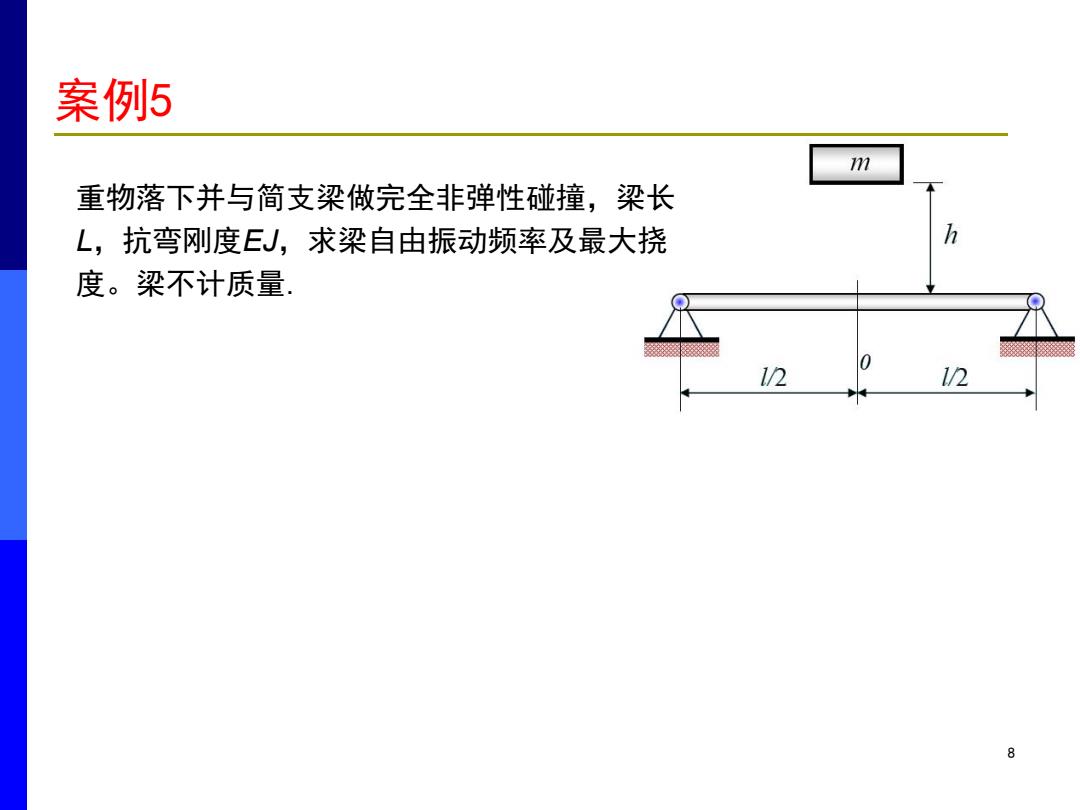
案例5 m 重物落下并与简支梁做完全非弹性碰撞,梁长 L,抗弯刚度EJ,求梁自由振动频率及最大挠 度。梁不计质量 12 12 8
8 重物落下并与简支梁做完全非弹性碰撞,梁长 L,抗弯刚度EJ,求梁自由振动频率及最大挠 度。梁不计质量. 案例5
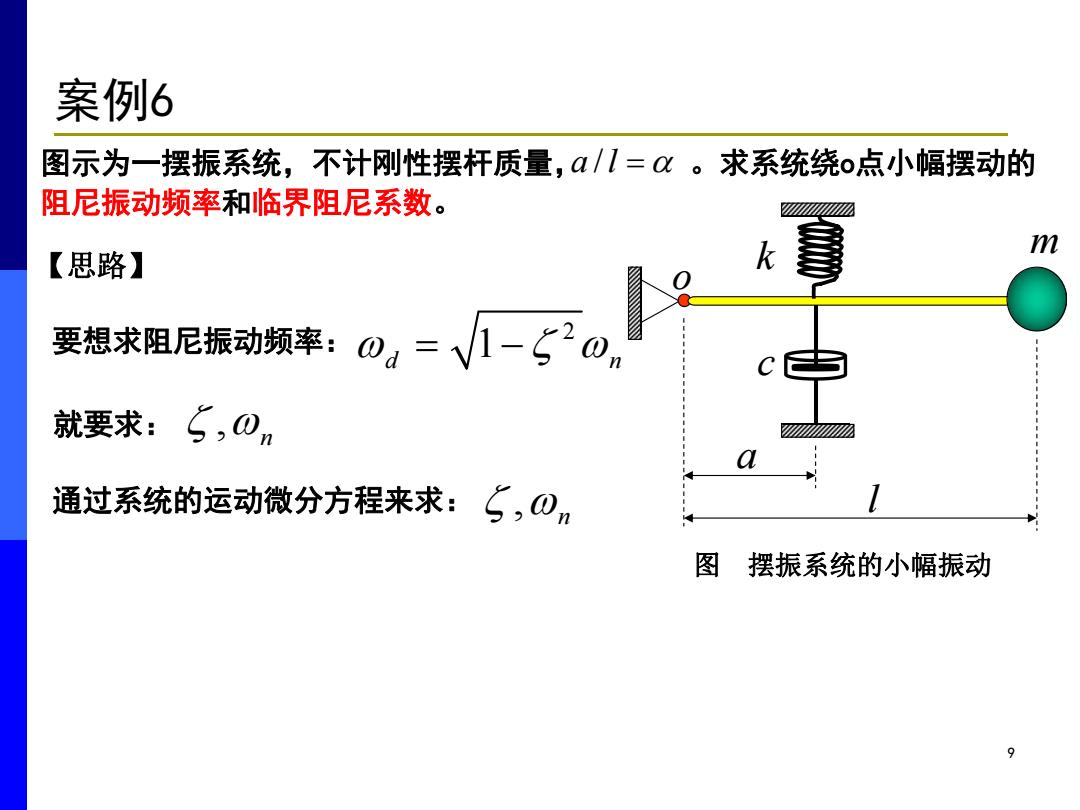
案例6 图示为一摆振系统,不计刚性摆杆质量,α/1=。求系统绕o点小幅摆动的 阻尼振动频率和临界阻尼系数。 【思路】 要想求阻尼振动频率:0,=√-专 就要求:5,0n 通过系统的运动微分方程来求:5,0m 图 摆振系统的小幅振动 9
9 图示为一摆振系统,不计刚性摆杆质量, 。求系统绕o点小幅摆动的 阻尼振动频率和临界阻尼系数。 c k m o a l a / l 图 摆振系统的小幅振动 【思路】 要想求阻尼振动频率: 2 1 d n 就要求: , n 通过系统的运动微分方程来求: , n 案例6

案例7 小球质量,刚杆质量不计,小球重量不计。写出(1)系统运动微分方程 ;(2)临界阻尼系数和有阻尼固有频率。 动力矩平衡建立系统运动微分方程 无阻尼固有频率: k m 阻尼比 5= 2.m.0m 有阻尼固有频率 04=0nV1-52 10
10 小球质量m,刚杆质量不计,小球重量不计。写出(1)系统运动微分方程 ;(2)临界阻尼系数和有阻尼固有频率。 θ 无阻尼固有频率: n k m 阻尼比 2. . n c m 2 1 d n 有阻尼固有频率 动力矩平衡建立系统运动微分方程 案例7
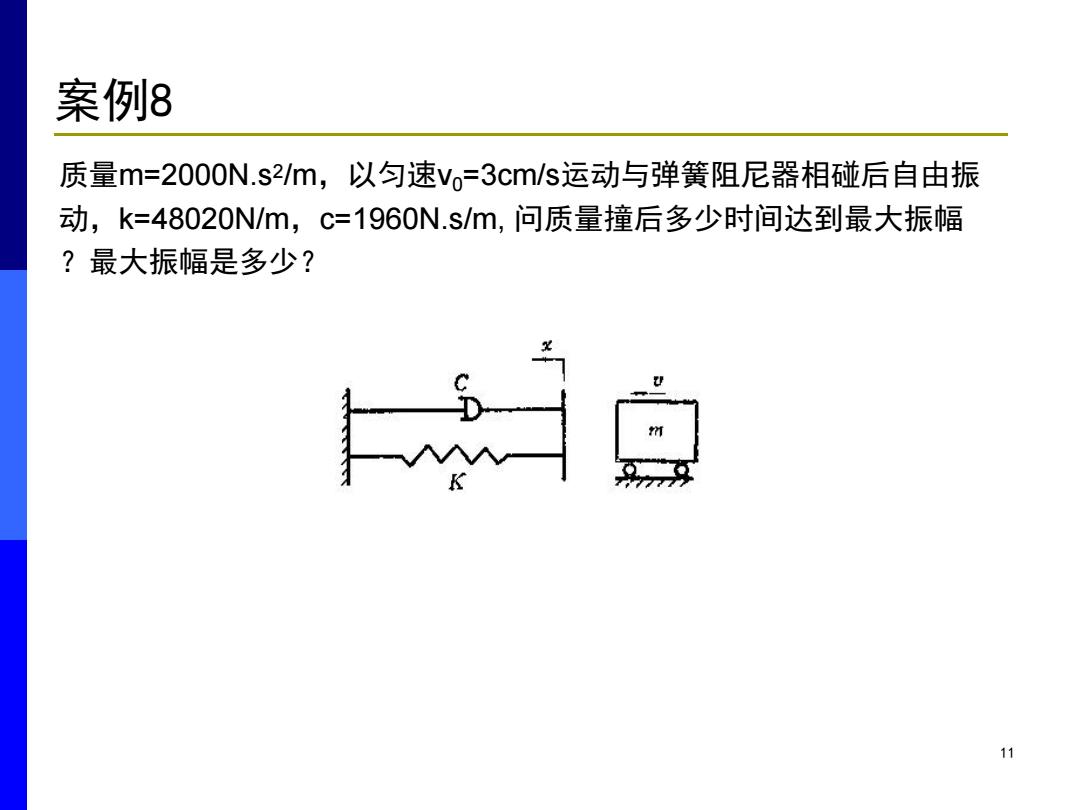
案例8 质量m=2000N.s2m,以匀速vo=3cm/s运动与弹簧阻尼器相碰后自由振 动,k=48020N/m,c=1960N.s/m,问质量撞后多少时间达到最大振幅 ?最大振幅是多少? 11
11 质量m=2000N.s2/m,以匀速v0=3cm/s运动与弹簧阻尼器相碰后自由振 动,k=48020N/m,c=1960N.s/m, 问质量撞后多少时间达到最大振幅 ?最大振幅是多少? 案例8