
电磁场的基本规律 Xidian University 本章内容 §I.1叠加原理(principle of super positionector analysis) §1.2电场(electric field) §1.3磁场(magnetic field) §1.4真空中的麦克斯韦方程Maxwel's equation in vacuum §1.5介质的电性质(Electric fields in matter) §1.6介质的磁化(magnetic fields in matter) §1.7电磁场的边值关系(boundary conditions) §1.8电磁场的能量和能流 (charge and Energy) 西安电子科技大学
西安电子科技大学 §1.1 叠加原理(principle of super positionector analysis) 本章内容 §1.2 电场(electric field) §1.3 磁场(magnetic field) §1.4 真空中的麦克斯韦方程Maxwell’s equation in vacuum §1.7 电磁场的边值关系(boundary conditions) §1.5介质的电性质(Electric fields in matter) §1.6介质的磁化(magnetic fields in matter) §1.8 电磁场的能量和能流(charge and Energy) 电磁场的基本规律

电磁场的基本规律 Xidian University §I.1叠加原理(principle of superpositionector analysis) 静电场:相对观察者静止的电荷分布产生的电场 叠加原理:又称为独立作用原理,来源于实验。 电场力的叠加原理指出:任意2个电荷之间的相互 作用力,完全与是否存在其他电荷无关。 电荷g与Q之间的作用力不仅与 两者间的距离还与彼此的速度 及加速度有关。 西安电子科技大学
西安电子科技大学 §1.1 叠加原理(principle of superpositionector analysis) 静电场:相对观察者静止的电荷分布产生的电场 叠加原理:又称为独立作用原理,来源于实验。 电场力的叠加原理指出:任意2个电荷之间的相互 作用力,完全与是否存在其他电荷无关。 F Q1 Qi 1 r q 电荷q与Qi之间的作用力不仅与 两者间的距离还与彼此的速度 及加速度有关。 Q2 电磁场的基本规律
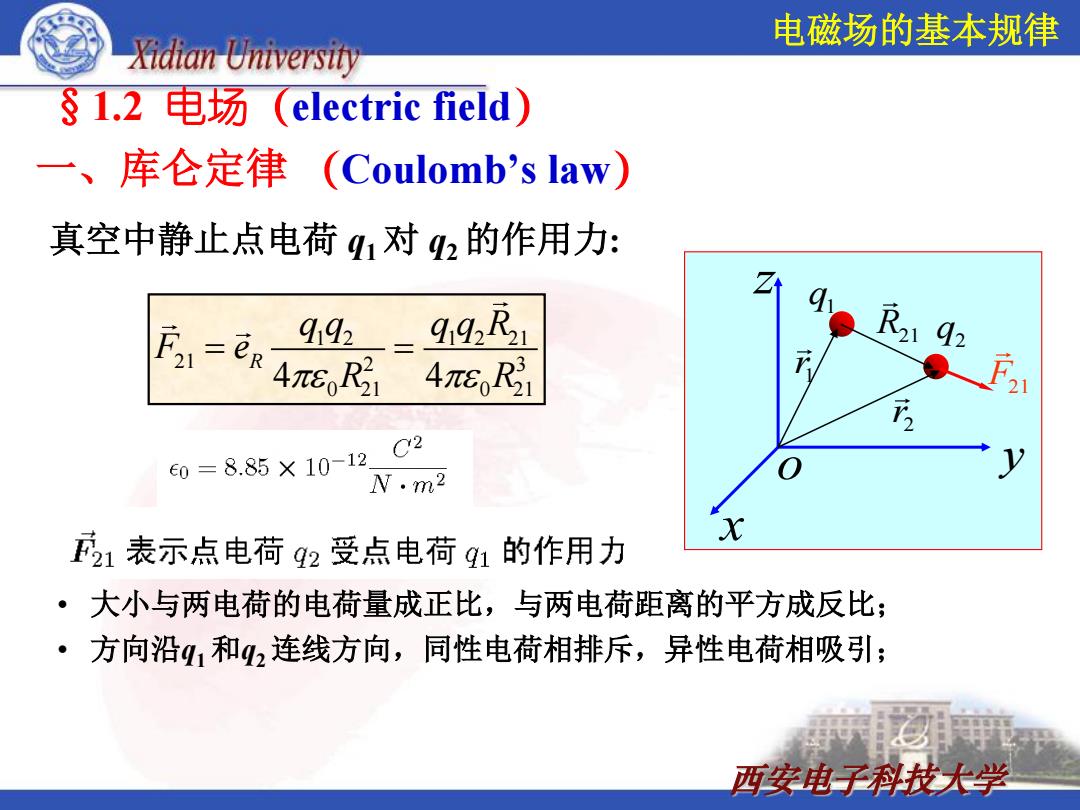
电磁场的基本规律 Xidian University §1.2电场(electric field) 一、库仑定律(Coulomb'slaw) 真空中静止点电荷q1对q2的作用力: Fa-ER4 9192- 919,R1 π6R31 4πR C2 0=8.85×10-12 N.m2 1表示点电荷g2受点电荷91的作用力 ·大小与两电荷的电荷量成正比,与两电荷距离的平方成反比; ·方向沿q1和2连线方向,同性电荷相排斥,异性电荷相吸引; 西安电子科技大学
西安电子科技大学 一、库仑定律 (Coulomb’s law) y x z o 1 r 1 q 2 r R21 F21 1 2 1 2 21 q2 21 2 3 0 21 0 21 4 4 R q q q q R F e R R 真空中静止点电荷 q1 对 q2 的作用力: • 大小与两电荷的电荷量成正比,与两电荷距离的平方成反比; • 方向沿q1 和q2 连线方向,同性电荷相排斥,异性电荷相吸引; §1.2 电场(electric field) 电磁场的基本规律

电磁场的基本规律 Xidian University 二、 电场强度(The electric field) 电场强度矢量 描述电场分布的基本物理量 空间某点的电场强度定义为置于该点的单位点电荷(又称 试验电荷)受到的作用力,即 E()=lim (行) 试验正电荷 90→0 90 根据上述定义,真空中静止点 电荷,激发的电场为: gR 京M尼 )= :(R=F- >电场是位置的函数 >电场与检验电荷无关 西安电子科技大学
西安电子科技大学 y x z o r q r R E M 空间某点的电场强度定义为置于该点的单位点电荷(又称 试验电荷)受到的作用力,即 0 0 0 ( ) ( ) lim q F r E r q 3 0 ( ) 4 qR E r R 根据上述定义,真空中静止点 电荷q 激发的电场为: ( ) R r r 电场强度矢量 E —— 描述电场分布的基本物理量 q0——试验正电荷 二、电场强度 (The electric field) 电场是位置的函数 电场与检验电荷无关 电磁场的基本规律

电磁场的基本规律 Xidian University 由叠加原理由多个点电荷构成电场 -∑= → 4环e0 (=4纸60 (- 下-3 2=1 电荷连续分布 (的= fp(r)(-) 7-3 注意: 1)矢量积分 2)若电荷分布已知可求出电场,但若电荷分布未 知,如何求静电场? 西安电子科技大学
西安电子科技大学 由叠加原理由多个点电荷构成电场 电荷连续分布 注意: 1)矢量积分 2)若电荷分布已知可求出电场,但若电荷分布未 知,如何求静电场? 电磁场的基本规律

电磁场的基本规律 Xidian University 三、高斯定理(Gauss'slaw) 1.静电场的高斯定理(积分形式) 重5)ds=JNv 2.高斯定理的微分形式(Differential form of Gauss'slaw) 又.(=又· dlr(-d 积分对进行,微分(V)作用于 4πe0 -3 故积分微分次序可交换 dr' 又作用于子,p()视为常数 r- dr' 利用又 - |7-8=4r6(7- p'r-rdr-p(的 En V.(=1p( 西安电子科技大学
西安电子科技大学 0 1 ( ) d ( )d S V E r S r V 1. 静电场的高斯定理(积分形式) 三、高斯定理 (Gauss’s law) 2.高斯定理的微分形式(Differential form of Gauss’s law) ) 电磁场的基本规律

Xidian Universit 电磁场的基本规律 四、静电场旋度(The curl of electrostatic field) 静电场的环路定理(积分形式)∮。E()d7=0 静电场的旋度(微分形式) V×(的=VX e()(F-dr 积分对子进行,微分作用于了 ATEO -3 故积分微分次序可交换 p()(r-) dr' 又作用于,p()视为常数 dr' 利用VX -3 0 V×(=0 或 E()·d=0 西安电子科技大学
西安电子科技大学 ( ) d 0 C E r l 静电场的旋度(微分形式) 静电场的环路定理(积分形式) 四、静电场旋度(The curl of electrostatic field) 或 电磁场的基本规律

电磁场的基本规律 Xidian University §1.3磁场(magnetic field) 一、电流与电流密度 电流一电荷的定向运动而形成,用i表示,其大小定义为: 单位时间内通过某一横截面$的电荷量,即 i=lim(△q/△t)=dq/dt △t0 单位:A(安培) 电流方向:正电荷的流动方向 定义电流密度矢量: 方向:沿该点上电流的方向 数值:单位时间垂直通过单位面积的电量 1=∫7 方与电流I的关系 西安电子科技大学
西安电子科技大学 §1.3 磁场(magnetic field) 一、电流与电流密度 单位: A (安培) 电流方向: 正电荷的流动方向 0 lim ( ) d d t i q t q t 电流 —— 电荷的定向运动而形成,用i 表示,其大小定义为: 单位时间内通过某一横截面S的电荷量,即 定义电流密度矢量: 方向:沿该点上电流的方向 数值:单位时间垂直通过单位面积的电量 S I j ds 与电流 I 的关系 电磁场的基本规律

电磁场的基本规律 Xidian University 二、电荷守恒定律 流出任意一闭合曲面的电量=该闭合曲面所围区域内电量的减少 d 散度 业 曲面不 定理 随t变 v.jdr at dr (local charge conservation) =0 8t (continuity equation) 稳恒电流: op at =0→V.方=0 四安电子科技大学
西安电子科技大学 二、电荷守恒定律 流出任意一闭合曲面的电量=该闭合曲面所围区域内电量的减少 (local charge conservation) (continuity equation) 稳恒电流: 电磁场的基本规律

电磁场的基本规律 Xidian University 三、毕奥-萨伐尔定律(Biot-Savart law) 任意电流回路C上电流元Id产生的磁场感应强度 dB()= 1d'×(行-) 4元 F-F 引入体电流密度则磁场感应强度为 1】 B()= 恒定电流的变换关系: 0=1.26×10-6H/m 电流: 90 fdl~ado T=入⑦, =0g8, 电荷: N入dlgdo } =p 西安电子科技大学
西安电子科技大学 三、毕奥-萨伐尔定律(Biot-Savart law) y x z o r I l d r R C M 0 3 ( ) ( ) d 4 V J r R B r V R 任意电流回路C上电流元 I l d 产生的磁场感应强度 引入体电流密度则磁场感应强度为 0 3 d ( ) d ( ) 4 I l r r B r r r 恒定电流的变换关系: 电磁场的基本规律