
课程特点 数学物理方法是物理学类、电子信息科 学类和通信科学类的重要公共基础课和工具。 主要特色在于数学和物理的紧密结合, 将数学用于实际的物理和交叉科学的实际问 题的分析中,通过物理过程建立数学模型 通过求解和分析模型,对具体物理过程的深 入理解。提高分析解决实际问题的能力。 2
2022/11/24 2 课程特点: 数学物理方法是物理学类、电子信息科 学类和通信科学类的重要公共基础课和工具。 主要特色在于数学和物理的紧密结合, 将数学用于实际的物理和交叉科学的实际问 题的分析中,通过物理过程建立数学模型, 通过求解和分析模型,对具体物理过程的深 入理解。提高分析解决实际问题的能力

出课程内容 第一章:微分几何(4) 第二章:线性空间 (4) 第三章:渐近方法 (5) 第四章:格林函数法 (5) 第五章:积分方程的解法(5) 12g 3
2022/11/24 3 课程内容: 第一章:微分几何(4) 第二章:线性空间(4) 第三章:渐近方法(5) 第四章:格林函数法(5) 第五章:积分方程的解法(5)

课程学习目标: 1、掌握微分几何、线性空间的相关定义和本征函数 集的应用; 2、掌握数学物理方程常规解法的技巧,以及特殊函 数的应用; 3、掌握格林函数在数学物理方法求解中的应用,掌 握积分方程的数值求解方法,学习数值渐近方法。 4、学习和提高编程分析实际问题的能力。 D1121
2022/11/24 4 课程学习目标: 1、掌握微分几何、线性空间的相关定义和本征函数 集的应用; 2、掌握数学物理方程常规解法的技巧,以及特殊函 数的应用; 3、掌握格林函数在数学物理方法求解中的应用,掌 握积分方程的数值求解方法,学习数值渐近方法。 4、学习和提高编程分析实际问题的能力

第一章微分几何 微分几何的产生和发展是与数学分析密切相连的, 在这方面做出突出贡献的有瑞士数学家欧拉,法国的 蒙日,德国的高斯、克莱因等 经近300年的发展,已逐渐成为数学上独具 特色,应用广泛的学科。 在波的辐射、传播、散射、反射等应用领域常 遇到对物体几何形状的分析,而微分几何所阐明 的概念和方法,在这一方面成为有力的工具。 2022/11/24 6
2022/11/24 6 第一章 微分几何 微分几何的产生和发展是与数学分析密切相连的, 在这方面做出突出贡献的有瑞士数学家欧拉,法国的 蒙日,德国的高斯、克莱因等。 在波的辐射、传播、散射、反射等应用领域常 遇到对物体几何形状的分析,而微分几何所阐明 的概念和方法,在这一方面成为有力的工具。 经近300年的发展,已逐渐成为数学上独具 特色,应用广泛的学科

第一章微分几何 微分几何是采用微积分的方法研究几何图形 的学科。本章重点讨论曲面理论的基本原理。 微分几何中,由于运用数学分析的理论,就可 以在无限小的范围内略去高阶无穷小,一些复杂 的依赖关系可以变成线性的,不均匀的过程也可 以变成均匀的,这些都是微分几何特有的研究方 法。 学习本章的重点是掌握微分几何基本概念理解 空间曲面的定义、定理及重要几何量的计算方法
2022/11/24 7 第一章 微分几何 微分几何是采用微积分的方法研究几何图形 的学科。本章重点讨论曲面理论的基本原理。 微分几何中,由于运用数学分析的理论,就可 以在无限小的范围内略去高阶无穷小,一些复杂 的依赖关系可以变成线性的,不均匀的过程也可 以变成均匀的,这些都是微分几何特有的研究方 法。 学习本章的重点是掌握微分几何基本概念理解 空间曲面的定义、定理及重要几何量的计算方法
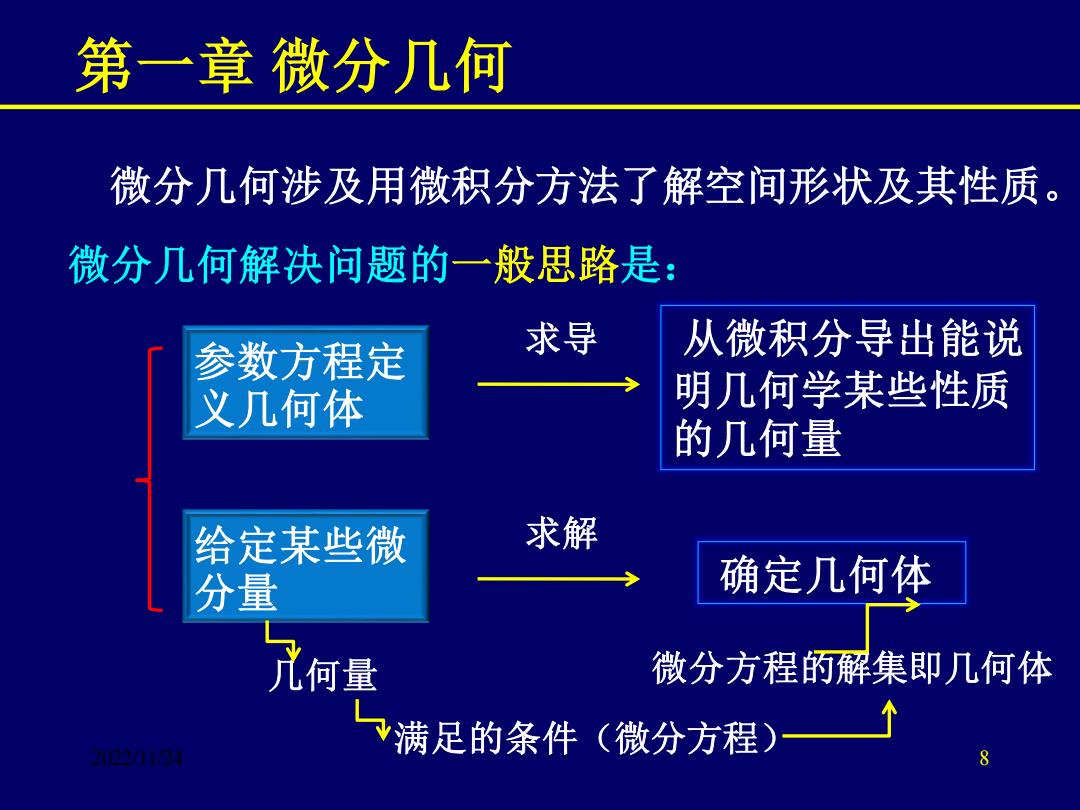
第一章微分几何 微分几何涉及用微积分方法了解空间形状及其性质。 微分几何解决问题的一般思路是: 参数方程定 求导 从微积分导出能说 义几何体 明几何学某些性质 的几何量 给定某些微 求解 分量 确定几何体 九何量 微分方程的解集即几何体 满足的条件(微分方程) 112g 8
2022/11/24 第一章 微分几何 微分几何涉及用微积分方法了解空间形状及其性质。 微分几何解决问题的一般思路是: 参数方程定 义几何体 求导 从微积分导出能说 明几何学某些性质 的几何量 给定某些微 分量 求解 确定几何体 几何量 满足的条件(微分方程) 微分方程的解集即几何体 8

第一章微分几何 1、三维空间中的曲线; 2、三维空间中的曲面 3、曲面的第一、二基本形式; 4、 曲面的曲率; 5、测地线 6、张量简述。 121 9
2022/11/24 9 第一章 微分几何 1、三维空间中的曲线; 2、三维空间中的曲面; 3、曲面的第一、二基本形式; 4、曲面的曲率; 5、测地线; 6、张量简述

:第一章微分几何 推荐用书: 《数学物理方法》王一平主编, 电子工业出版社 《微分几何的理论和习题》利普舒茨著,上海科学 技术出版社 《微分几何讲义》陈省身陈维恒著,北京大学出 版社 《微分几何》梅向明黄敬之编,高等教育出版社 1121 10
2022/11/24 10 : 推荐用书: 《数学物理方法》王一平主编,电子工业出版社 《微分几何的理论和习题》利普舒茨著,上海科学 技术出版社 《微分几何讲义》陈省身 陈维恒著,北京大学出 版社 《微分几何》梅向明 黄敬之编,高等教育出版社 第一章 微分几何

§1.1.1曲线的表示 §1.1三维空间中的曲线 一、曲线的表示 在E3中Descartes直角坐标系O-yz下运动质点的位置为 F(t)=x(t)i+y(t)j+z(t)k 其中i,,k为单位正交基向量, 空间曲线定义: 区间(a,b)上点t在映射:t>(x(),y),)下像的集合 曲线C的表示: C可用向量形式的参数方程表示为 F(t)=x(t)i+y(t)j+=()k=[x(t),y(t),=(t)] 或写为分量形式的参数方程 术=) y=y(t),tE(a,b). 式中t称为C的参数 2=()
2022/11/24 11 § 1.1 三维空间中的曲线 在 E3 中Descartes直角坐标系 O-xyz 下运动质点的位置为 其中 为单位正交基向量. 空间曲线定义: 区间(a, b)上点t 在映射:t→ (x(t), y(t), z(t)) 下像的集合 曲线C的表示: § 1.1.1 曲线的表示 式中t 称为 C 的参数 C 可用向量形式的参数方程表示为 或写为分量形式的参数方程 x = x(t) y = y(t) z = z(t) , t(a, b) . 一、曲线的表示 r t x t i y t j z t k ( ) ( ) ( ) ( ) = + + i j k , , r t x t i y t j z t k x t y t z t ( ) ( ) ( ) ( ) [ ( ), ( ), ( )] = + + =

§1.1.1曲线的表示 §1.1三维空间中的曲线 二、正则 假定所研究的曲线r(t)至少是t的一阶连续可微函数。 定义:如果给定参数曲线C:下=T(t),t∈(a,b). 若)10,则称t=的对应点)为C的一个正则点。 若)=0,则称t=t的对应点()为C的一个奇点: 若曲线上所有点正则,则称C为正则曲线,并称参数t为正 则参数, 几何意义: 视参数曲线为动点轨迹,正则点的几何意义则是当参数在该点 处作微小变动时动点的位置同时作真正的变动
2022/11/24 12 § 1.1 三维空间中的曲线 假定所研究的曲线 至少是t 的一阶连续可微函数。 § 1.1.1 曲线的表示 二、正则 定义 :如果给定参数曲线C: , t(a, b) . • 若 ,则称 t = t0 的对应点 为 C 的一个正则点. • 若 ,则称 t = t0 的对应点 为 C 的一个奇点; 若曲线上所有点正则,则称C 为正则曲线,并称参数t 为正 则参数. 几何意义: • 视参数曲线为动点轨迹,正则点的几何意义则是当参数在该点 处作微小变动时动点的位置同时作真正的变动. r r t = ( ) r t( ) 0 r t ¢( ) 0 ¹ 0 r t( )0 r t( ) 0 r t ¢( ) 0 =