上海交通大学：《物理实验》精品课程教学资源（讲义）核磁共振成像（自旋回波原理）

实验7-2自旋回波 自旋回波(Spin Echo)是射频脉冲与静磁场中核磁矩体系相互作用的结果。两个具有适当 宽度的射频脉冲以一定的间隔相继作用在静磁场中 的核磁矩体系上，经过一段时间在接收系统中会出 现一个感应信号，信号与第二脉冲的间隔恰好等于 脉冲之间的间隔，就象脉冲信号的回波一样，故称 为“自旋回波”。图7-2-1是自旋回波的示意图。 自旋回波不仅是一种有趣的物理现象，而且也 是一项重要的实验技术。利用自旋回波技术可以测 01 T+21 量弛豫时间T1和T2,特别是可剔除磁场不均匀对 T2的影响。还可以研究所谓“自扩散效应”。 图7-2-1自旋回波 一、实验目的 1.用实验手段研究射频脉冲与静磁场中核磁矩体系的相互作用，学会用矢量模型介释 实验现象。 2.用自旋回波方法测量T2。 3.用射频脉冲法测量T1。 二、实验原理 1.自由感应衰减FD) 2 M 0 (b) (c 图7-2-2自由感应衰减(FID) 173

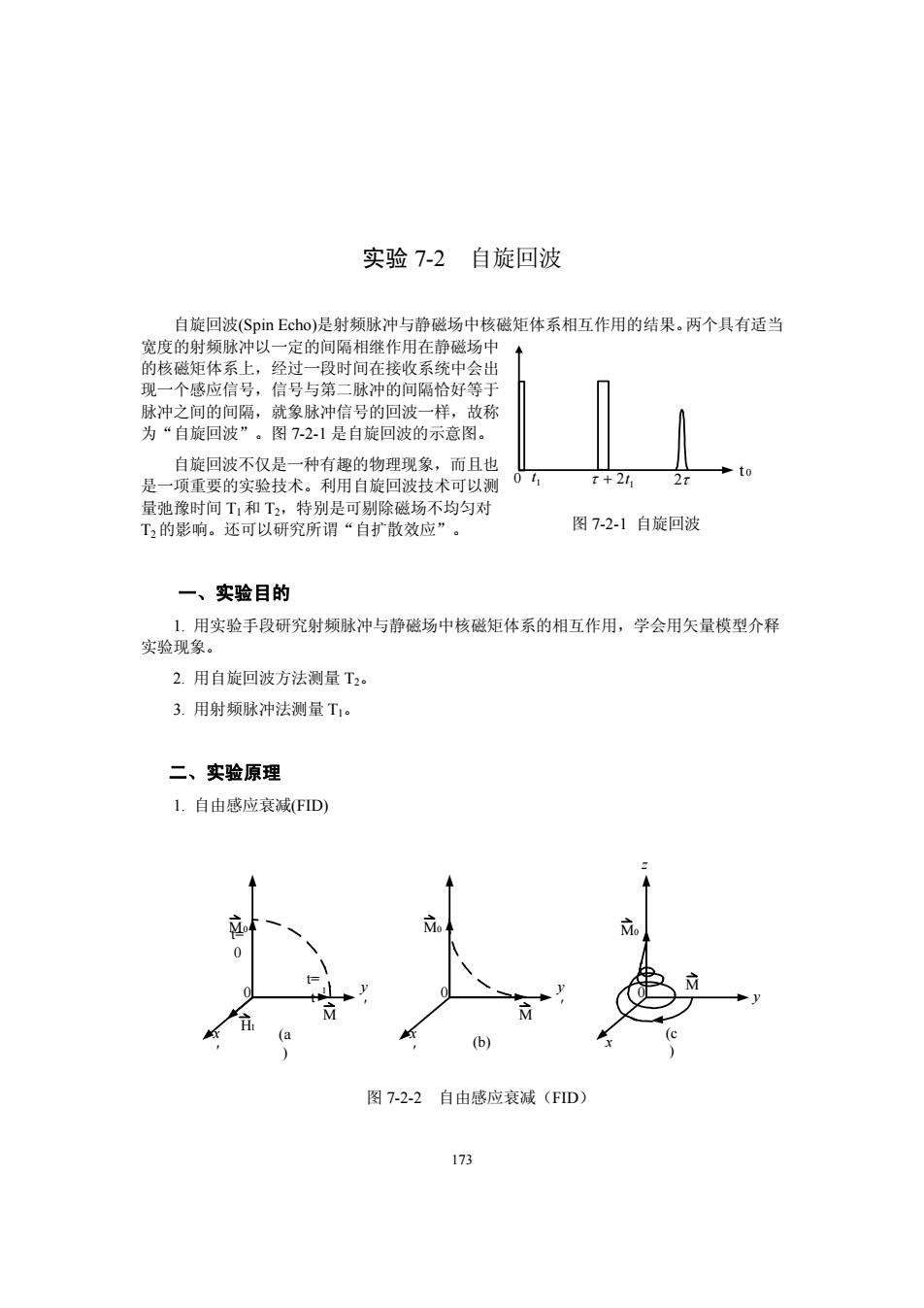
173 实验 7-2 自旋回波 自旋回波(Spin Echo)是射频脉冲与静磁场中核磁矩体系相互作用的结果。两个具有适当 宽度的射频脉冲以一定的间隔相继作用在静磁场中 的核磁矩体系上，经过一段时间在接收系统中会出 现一个感应信号，信号与第二脉冲的间隔恰好等于 脉冲之间的间隔，就象脉冲信号的回波一样，故称 为“自旋回波”。图 7-2-1 是自旋回波的示意图。 自旋回波不仅是一种有趣的物理现象，而且也 是一项重要的实验技术。利用自旋回波技术可以测 量弛豫时间 T1 和 T2，特别是可剔除磁场不均匀对 T2 的影响。还可以研究所谓“自扩散效应”。 一、实验目的 1. 用实验手段研究射频脉冲与静磁场中核磁矩体系的相互作用，学会用矢量模型介释 实验现象。 2. 用自旋回波方法测量 T2。 3. 用射频脉冲法测量 T1。 二、实验原理 1. 自由感应衰减(FID) t 0 0 t1 τ + 2t1 2τ 图 7-2-1 自旋回波 y ' x ' 0 t= t 1 t= 0 y ' x ' 0 z y x 0 M0 M0 M M0 M M H1 (a ) (b) (c ) 图 7-2-2 自由感应衰减（FID）

磁共振的宏观理论告诉我们，满足共振条件时，磁化强度矢量M在旋转坐标系中将绕H,以 o1=H的角频率进动。假设H,在0的时刻加上，在t=11=π/201=π/2rH时撤去， 那么在0~1这段时间里M绕H,恰好转过90（图7-2-2）。这个脉冲的作用是使M转过90°， 故称为90°脉冲。显然的大小与H有关，当H很强时，1可能比系统的弛豫时间T1、T2 小得多，这正是用射频脉冲激发磁矩系统的基本要求。（为什么？） 根据Bloch的假设，射频脉冲撤去以后M的纵向分量M,和横向分量My将各自按指数 规律回到原先的平衡位置： dM:M。-M dt T 0=o-月-司 M M(1)=M(O)e 弛豫过程在x'y'z系中观察如图7-2-1b所示。在xz系中观察则如图7-2-2c所示。弛豫时 间过程中M≠0，所以在接受线圈（在自差法中这个线圈也是发射线圈）中将感应出一个 信号，感应信号的频率与进动频率0。相同，其包络与M的大小成比例。这样一个频率为 o。的指数衰减信号称为自由感应衰减信号，即FD信号。理论分析表明（图7-2-3），FID FID信号 载波00 0t1 (a)调制在载波上的FID信号 (b)检波（介调）后得到的FID信号 图7-2-3FID信号 信号（时域信号）与波谱（频域信号）互为付里叶变换。在PFT-NMR系统中就是利用计算机对 -0 00 FID信号 FID信号 图7-2-4时域信号和频域信号之间的变换 FD信号进行快速付里叶变换以后得到波谱的（图7-24）。 (图7-2-3a)表示FID信号的幅度正比于e及，实际上由于外磁场H。的不均匀，样品中 174

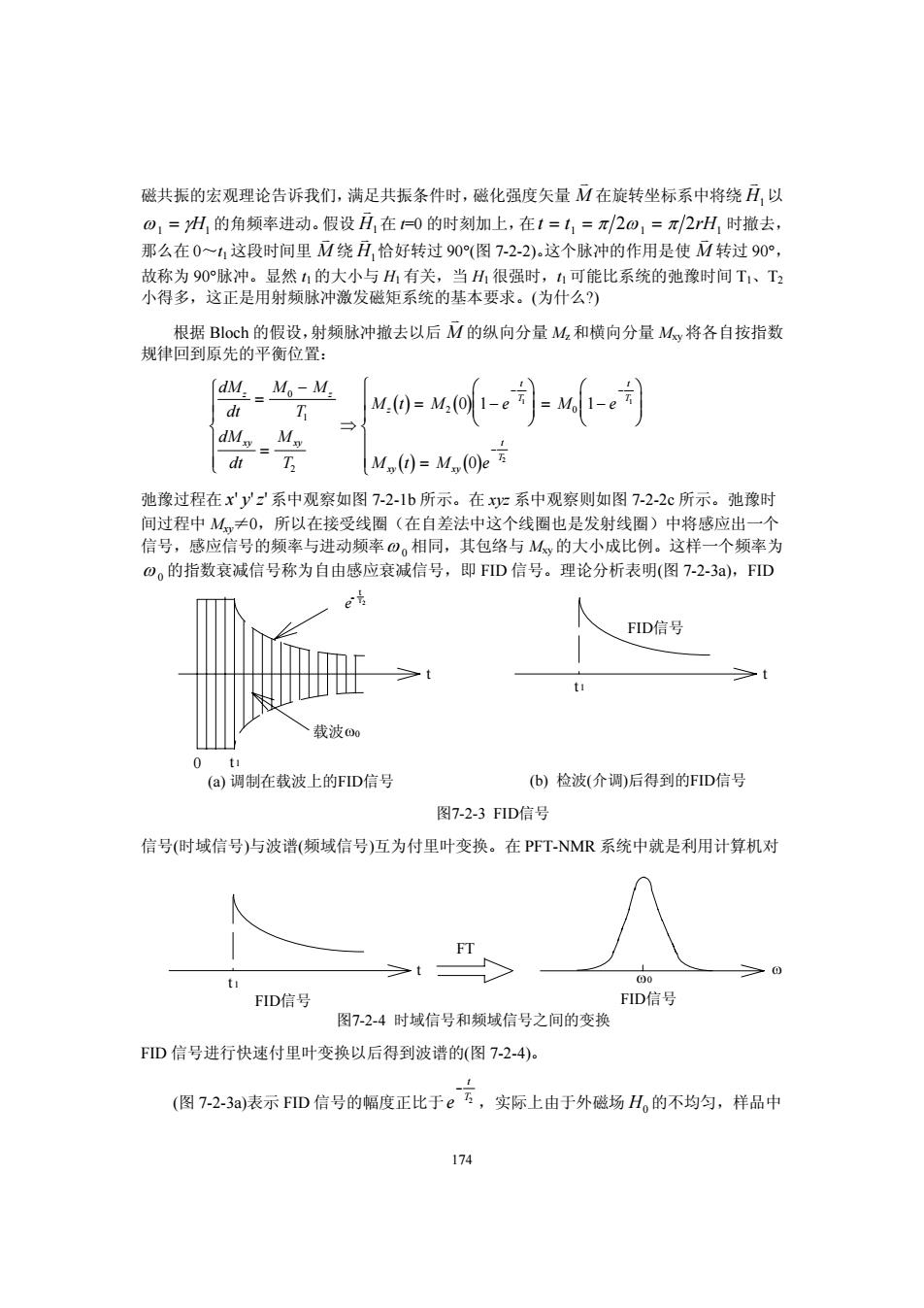
174 磁共振的宏观理论告诉我们，满足共振条件时，磁化强度矢量 K M 在旋转坐标系中将绕 K H1以 ω γ 1 1 = H 的角频率进动。假设 K H1在 t=0 的时刻加上，在t t rH = 11 1 = π 2 2 ω = π 时撤去， 那么在 0～t1 这段时间里 K M 绕 K H1恰好转过 90°(图 7-2-2)。这个脉冲的作用是使 K M 转过 90°， 故称为 90°脉冲。显然 t1 的大小与 H1 有关，当 H1 很强时，t1 可能比系统的弛豫时间 T1、T2 小得多，这正是用射频脉冲激发磁矩系统的基本要求。(为什么?) 根据 Bloch 的假设，射频脉冲撤去以后 K M 的纵向分量 Mz和横向分量 Mxy将各自按指数 规律回到原先的平衡位置： () ( ) () ( ) dM dt M M T dM dt M T Mt M e M e Mt M e z z xy xy z t T t T xy xy t T = − = ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ ⇒ = − ⎛ ⎝ ⎜ ⎜ ⎞ ⎠ ⎟ ⎟ = − ⎛ ⎝ ⎜ ⎜ ⎞ ⎠ ⎟ ⎟ = ⎧ ⎨ ⎪ ⎪ ⎩ ⎪ ⎪ − − − 0 1 2 2 0 01 1 0 1 1 2 弛豫过程在 x' '' y z 系中观察如图 7-2-1b 所示。在 xyz 系中观察则如图 7-2-2c 所示。弛豫时 间过程中 Mxy≠0，所以在接受线圈（在自差法中这个线圈也是发射线圈）中将感应出一个 信号，感应信号的频率与进动频率ω 0 相同，其包络与 Mxy的大小成比例。这样一个频率为 ω 0 的指数衰减信号称为自由感应衰减信号，即 FID 信号。理论分析表明(图 7-2-3a)，FID 信号(时域信号)与波谱(频域信号)互为付里叶变换。在 PFT-NMR 系统中就是利用计算机对 FID 信号进行快速付里叶变换以后得到波谱的(图 7-2-4)。 (图 7-2-3a)表示 FID 信号的幅度正比于e t T − 2 ，实际上由于外磁场 H0 的不均匀，样品中 载波 0 t 1 ω0 t e - t T2 t t 1 FID信号 (a) 调制在载波上的FID信号 (b) 检波(介调)后得到的FID信号 图7-2-3 FID信号 t t 1 FID信号 FT ω ω0 FID信号 图7-2-4 时域信号和频域信号之间的变换

不同核磁矩所处场大小不同，衰减时进动频率不相同，不同进动频率的指数衰减信号叠加 的结果使总和的FD信号以T2"衰减，T2"满足 111 TLT 其中五是Bloch定义的横向弛豫时间，而T,则反映了外场H,的不均匀T,一 -)。T2 H 的作用相当于使上能级的寿命缩短，从而使谱线展宽，用NMR方法通过测量线宽来计算 T2时实际上将T2'的影响也包含进去了。对液体样品来说，T2'常比T2要小得多，所以用线 宽来衡量T2是不合适的，以下我们将看到自旋回波技术就可以避免T2'的影响。 2.自旋回波(Spin Echo) 和自由感应衰减一样，自旋回波也可以用矢量模型来解释。 ≥y M t=0 tt (a) (b) (c) M M t=t+2ti =2r (d) (e) 图7-2-590°-t-180°自旋回波矢量图解 设磁场不太均匀，T2"<T2,观察自旋回波时用两个射频脉冲，第一个从=0到=1的是 “90°脉冲”，在τ时刻(T2"<t<T1,T2)加上第二个“180°脉冲”（脉冲持续时间比第一个 长一倍)，我们来分析这时M的运动。在图7-2-5中，(a)是=0的情况，(b)是=时的情况。 M绕丑进动90，到达x'-y面上的y轴，随后可接收到自由进动信号，它以时间常数T2” 衰减至零（图7-2-6）。这个过程相当于不同磁场处的局部磁化强度矢量M,在x-y平面上分 散成均匀分布。这分散主要不是由于自旋一自旋弛豫作用，而是由于外磁场的不均匀。我 175

175 不同核磁矩所处场大小不同，衰减时进动频率不相同，不同进动频率的指数衰减信号叠加 的结果使总和的 FID 信号以 T2"衰减，T2"满足 1 11 T2 T2 T2 " ' = + 其中 T2 是 Bloch 定义的横向弛豫时间，而 T2'，则反映了外场 H0 的不均匀(T2'= 1 0 γΔH )。T2' 的作用相当于使上能级的寿命缩短，从而使谱线展宽，用 NMR 方法通过测量线宽来计算 T2 时实际上将 T2'的影响也包含进去了。对液体样品来说，T2'常比 T2 要小得多，所以用线 宽来衡量 T2 是不合适的，以下我们将看到自旋回波技术就可以避免 T2'的影响。 2. 自旋回波(Spin Echo) 和自由感应衰减一样，自旋回波也可以用矢量模型来解释。 设磁场不太均匀，T2"<T2，观察自旋回波时用两个射频脉冲，第一个从 t=0 到 t=t1 的是 “90°脉冲”，在τ时刻(T2"<τ<<T1，T2)加上第二个“180°脉冲”(脉冲持续时间比第一个 长一倍)，我们来分析这时 K M 的运动。在图 7-2-5 中，(a)是 t=0 的情况，(b)是 t=t1 时的情况。 K M 绕 K H1进动 90，到达 x' ' −y 面上的 y' 轴，随后可接收到自由进动信号，它以时间常数 T2" 衰减至零(图 7-2-6)。这个过程相当于不同磁场处的局部磁化强度矢量 K Mi 在 x' ' −y 平面上分 散成均匀分布。这分散主要不是由于自旋⎯自旋弛豫作用，而是由于外磁场的不均匀。我 z' y' x' 0 t=0 M0 M B1 (a) z' y' x' 0 t=t1 M (b) z' y' x' t=t1 M2 M1 t=τ (c) z' y' x' M'2 M'1 t=τ (d) +2 z' y' x' M t=2τ (e) 0 图7-2-5 90 180 o −τ − o自旋回波矢量图解 t1

们挑出样品中两个微小部分，它们各处于稍 微不同的磁场中，它们的磁化强度矢量M, 和M,在旋转坐标中各自沿相反方向绕z轴 e-VT 进动，前者所处的磁场比平均磁场大，后者 所处的磁场比平均磁场小，在仁t时刻到达 图7-2-5c的位置。在这时加上第二个脉冲 (“180脉冲”宽度为21)，使它们分别转到 0 t t +2t 2t 图7-2-5d的M,'和M,'位置。从这位置起， M,'和M,'继续转，经过又一个t间隔，二 者又重合在-y方向上（图7-2-5e)。显然，其 图7-2-690°-180°脉冲系列测量T2 它各个M,此刻均相遇于-y方向上。因此，在线圈上又获得一个信号。这就是“回波”信 号（图7-2-6）。但是，由于存在自旋一自旋弛豫作用，回波信号的强度有所减弱。与90°脉冲 后的自由感应衰减信号相比，幅度下降到2。从实验上测定对应于不同x的回波信号 的相对幅度就可以准确地测定T2,而与磁场的均匀性无关。 3.用90°一T一90°脉冲序列测量T1 90°一τ一90°脉冲系列可用于测量纵向弛豫时间T(图7-2-7)。第一个90°脉冲使M绕 丑进动了90°，到达x'-y 平面的y轴上（图7-2-7b)。 随后由于外磁场的不均匀， 各磁化强度矢量在x'-y平 面上的分量经过T2"时间以 后，将成为均匀分布。同时 由于存在弛豫时间T,系统 0 磁矩M在：方向的分量 M.,将按(7-2-1)式指数增 B t=0 t=t 加，在仁t时刻，如图7-2-7c (a) (b) 所示。这时加上第二个90 脉冲。第二个90°脉冲过后， Mz(t)又倒至y轴的位 置，见图7-2-7d。这时紧接 Mz(t) àz) 着接收到的自由感应衰减信 号的起始振幅正比于 M2(t)(图7-2-8)。对于不同 M =t+t 的T,用90°-t-90°脉冲 t=t 系列测量M2(x)与t之间 (c) (d) 的关系，即可根据(7-2-1)式 图7-2-790°-t-90°脉冲系列波矢量图解 测定纵向弛豫时间T1。 176

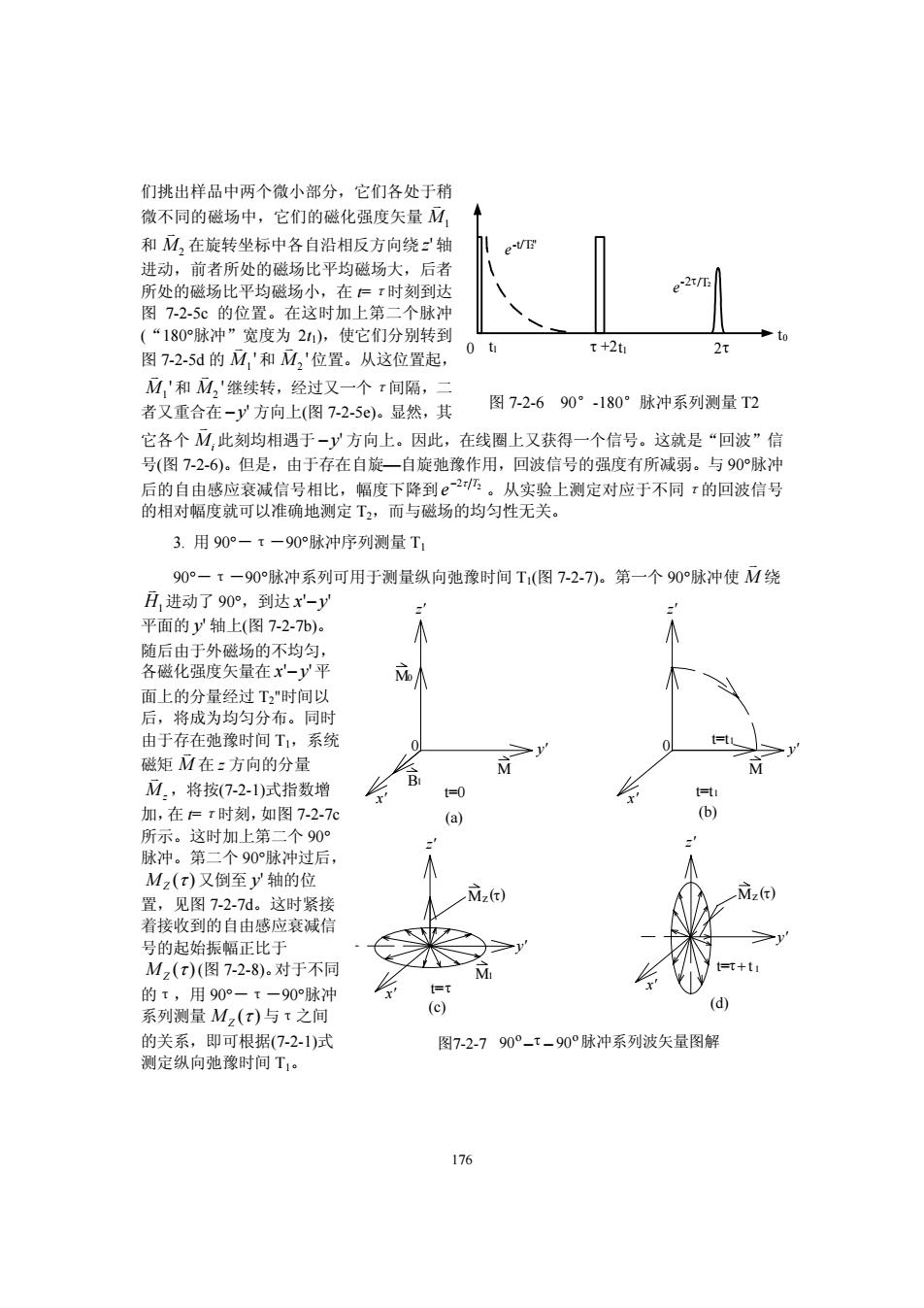
176 们挑出样品中两个微小部分，它们各处于稍 微不同的磁场中，它们的磁化强度矢量 K M1 和 K M2 在旋转坐标中各自沿相反方向绕 z' 轴 进动，前者所处的磁场比平均磁场大，后者 所处的磁场比平均磁场小，在 t=τ时刻到达 图 7-2-5c 的位置。在这时加上第二个脉冲 (“180°脉冲”宽度为 2t1)，使它们分别转到 图 7-2-5d 的 K M1 '和 K M2 '位置。从这位置起， K M1 '和 K M2 '继续转，经过又一个τ间隔，二 者又重合在 −y' 方向上(图 7-2-5e)。显然，其 它各个 K Mi 此刻均相遇于 −y' 方向上。因此，在线圈上又获得一个信号。这就是“回波”信 号(图 7-2-6)。但是，由于存在自旋⎯自旋弛豫作用，回波信号的强度有所减弱。与 90°脉冲 后的自由感应衰减信号相比，幅度下降到e −2 T2 τ 。从实验上测定对应于不同τ的回波信号 的相对幅度就可以准确地测定 T2，而与磁场的均匀性无关。 3. 用 90°－τ－90°脉冲序列测量 T1 90°－τ－90°脉冲系列可用于测量纵向弛豫时间 T1(图 7-2-7)。第一个 90°脉冲使 K M 绕 K H1进动了 90°，到达 x' ' −y 平面的 y' 轴上(图 7-2-7b)。 随后由于外磁场的不均匀， 各磁化强度矢量在 x' ' −y 平 面上的分量经过 T2"时间以 后，将成为均匀分布。同时 由于存在弛豫时间 T1，系统 磁矩 K M 在 z 方向的分量 K Mz ，将按(7-2-1)式指数增 加，在 t=τ时刻，如图 7-2-7c 所示。这时加上第二个 90° 脉冲。第二个 90°脉冲过后， MZ ( ) τ 又倒至 y' 轴的位 置，见图 7-2-7d。这时紧接 着接收到的自由感应衰减信 号的起始振幅正比于 MZ ( ) τ (图 7-2-8)。对于不同 的τ，用 90°－τ－90°脉冲 系列测量 MZ ( ) τ 与τ之间 的关系，即可根据(7-2-1)式 测定纵向弛豫时间 T1。 0 t1 2τ t0 e-t/T"2 τ +2t1 e-2τ/T2 图 7-2-6 90°-180°脉冲系列测量 T2 z' y' x' 0 t=0 M0 M B1 (a) z' y' x' 0 t=t1 M (b) z' y' x' t=t1 Mz M1 t=τ (c) z' y' x' t=τ (d) + 图7-2-7 90 90 o −τ − o脉冲系列波矢量图解 t 1 ( ) τ Mz ( ) τ

二、实验装置 实验装置如图7-2-9所示。 脉冲程序器用于产生90°一τ一180°或 90°一t一90°脉冲序列，两个脉冲的宽度、 间隔及脉冲序列的重复频率均可调。射频发 正比于z() 射机在脉冲序列的控制下发送频率为⊙。 ≥t tt+2ti 的射频脉冲序列去激励样品。仪器使用单线 图7-2-890°-τ-90°脉冲系列测量T1 圈探头，发射和接收由同一个线圈完成，探 头还包括调配电路和由二极管构成的自动开关，使发射和接收都能工作在良好的状态下。 接收放大器包括射频放大、检波和低频放大，输出信号送到示波器观察，同时送到一个单 点取样积分器，积分后用表头指示回波幅度。取样位置由来自脉冲程序器的取样脉冲控制。 脉冲程序器还输出一个同步脉冲作为示波器x轴的触发信号。 单点取 样积分 表头 回波信号 接收探头 脉，冲 射频 接收 程序器 发射机 放大器 同步脉冲 图7-2-9自旋回波实验装置 三、实验内容和要求 1.熟悉仪器，观察脉冲序列波形和射频冲序列波形，了解脉冲宽度、间隔及重复周期 的调节方法及调节范围。 2.观察甘油样品的FD信号 提示：①测量射频脉冲频率0o,利用共振条件及H的旋磁比数值Y=26753rad/S·G 计算Ho,并设定Ho(以后还需细调)。②适当选取脉冲间隔τ及周期T。 3.观察甘油样品的自旋回波信号 注意：不满足90°一τ一180°脉冲序列时也会看到回波信号，但90°一T一180°脉冲序列 作用下回波信号最强。 177

177 二、 实验装置 实验装置如图 7-2-9 所示。 脉冲程序器用于产生 90°－τ－180°或 90°－τ－90°脉冲序列，两个脉冲的宽度、 间隔及脉冲序列的重复频率均可调。射频发 射机在脉冲序列的控制下发送频率为ω 0 的射频脉冲序列去激励样品。仪器使用单线 圈探头，发射和接收由同一个线圈完成，探 头还包括调配电路和由二极管构成的自动开关，使发射和接收都能工作在良好的状态下。 接收放大器包括射频放大、检波和低频放大，输出信号送到示波器观察，同时送到一个单 点取样积分器，积分后用表头指示回波幅度。取样位置由来自脉冲程序器的取样脉冲控制。 脉冲程序器还输出一个同步脉冲作为示波器 x 轴的触发信号。 三、实验内容和要求 1. 熟悉仪器，观察脉冲序列波形和射频冲序列波形，了解脉冲宽度、间隔及重复周期 的调节方法及调节范围。 2. 观察甘油样品的 FID 信号 提示：①测量射频脉冲频率ω 0 ，利用共振条件及 H 的旋磁比数值γH=26753rad/S·G 计算 H0，并设定 H0（以后还需细调）。②适当选取脉冲间隔τ及周期 T。 3. 观察甘油样品的自旋回波信号 注意:不满足 90°－τ－180°脉冲序列时也会看到回波信号，但 90°－τ－180°脉冲序列 作用下回波信号最强。 0 t1 τ τ+2t1 t 图7-2-8 90 90 o o − −τ 脉冲系列测量T1 e-t/T"2 正比于Mz ( ) τ S N 接 收 放大器 单点取 样积分 射 频 发射机 脉 冲 程序器 Y X 表头 回波信号 接收探头 同步脉冲 图7-2-9 自旋回波实验装置

4.测量一组不同浓度的硫酸铜水溶液样品的弛豫时间T1,在双对数纸上作T~”” 图。 C+是一种顺磁离子，水中含有C+将剧烈改变质子磁矩的弛豫时间T1,这组测量可以 得到顺磁离子影响弛豫过程的规律。虽然可以用90°一t一90°脉冲序列直接测量T1,但是 具体操作有不便之处。由于常温水溶液T=T2,所以我们可以用90°一t一180°脉冲序列， 即用自旋回波方法测量T2,从而间接得到T1。至于直接测量T1的方法你当然可以尝试并体 会一下何处不便。原则上T2可由回波峰值和τ的曲线求得，但那样需要对每一个τ单独作 一次测量，工作量太大。实际上按下面的方法只要作两次测量就可以求得T2,设回波峰值 为A,已经知道 Acen 如果令两次测量得到的回波峰值A/A2=2,即 A e -=2 A. 2 e 两边取对数，整理即得 T3= 2(2-t) ≈2.89(t2-t1 In2 对于粘滞样品（如甘油），上述结论是正确的，但是非粘液体（例如水溶液），则因分子扩 散的影响，要进行修正。 由前面的讨论我们知道，在180°脉冲过后经过时间t,M又重新会聚形式自旋回波。 但是，是否所有的M,都能准确会聚，则取决于2τ时间内，每个核是否保持在不变的磁场 内。对于非粘滞液体，扩散会使核从不均匀磁场的一个区域运动到另一个区域，回波的幅 度将减小。 在自旋回波实验中，扩散效应对回波幅度的影响取决于空间磁场梯度(G)扩散系数(D) 和扩散发生的时间，己证明： 212yGDr Ace五3 其中y是旋磁比。令 K=2YGD 3 则 4e宗 同样令A/A2=2,则 178

178 4. 测量一组不同浓度的硫酸铜水溶液样品的弛豫时间 T1，在双对数纸上作T n 1 Cu ~ + + 图。 Cu ++ 是一种顺磁离子，水中含有Cu ++ 将剧烈改变质子磁矩的弛豫时间 T1，这组测量可以 得到顺磁离子影响弛豫过程的规律。虽然可以用 90°－τ－90°脉冲序列直接测量 T1，但是 具体操作有不便之处。由于常温水溶液 T1=T2，所以我们可以用 90°－τ－180°脉冲序列， 即用自旋回波方法测量 T2，从而间接得到 T1。至于直接测量 T1 的方法你当然可以尝试并体 会一下何处不便。原则上 T2 可由回波峰值和τ的曲线求得，但那样需要对每一个τ单独作 一次测量，工作量太大。实际上按下面的方法只要作两次测量就可以求得 T2，设回波峰值 为 A，已经知道 A e T ∝ − 2 2 τ 如果令两次测量得到的回波峰值 A1/A2=2，即 A A e e T T 1 2 2 2 1 2 2 2 = = 2 − − τ τ 两边取对数，整理即得 ( ) T2 ( ) 2 1 2 1 2 2 = 2 89 − ≈ − τ τ τ τ ln . 对于粘滞样品(如甘油)，上述结论是正确的，但是非粘液体(例如水溶液)，则因分子扩 散的影响，要进行修正。 由前面的讨论我们知道，在 180°脉冲过后经过时间τ， K Mi 又重新会聚形式自旋回波。 但是，是否所有的 K Mi 都能准确会聚，则取决于 2τ时间内，每个核是否保持在不变的磁场 内。对于非粘滞液体，扩散会使核从不均匀磁场的一个区域运动到另一个区域，回波的幅 度将减小。 在自旋回波实验中，扩散效应对回波幅度的影响取决于空间磁场梯度(G)扩散系数(D) 和扩散发生的时间，已证明： A e T G D ∝ − − 2 2 2 3 τ 22 3 γ τ 其中γ是旋磁比。令 K GD = 2 3 2 2 γ 则 A e T K ∝ − − 2 2 τ 3 τ 同样令 A1/A2=2，则

2(x2-t) ln2-K(-) 常数K可以从标准样品测量得到。已知25℃的水T2=2.3S,所以对于水样品 k-[n2--r小a 思考题 试用矢量模型分析M在180°.t-90°脉冲作用下的运动情况。 179

179 ( ) ( ) T K 2 2 1 2 3 1 3 2 2 = − − − τ τ ln τ τ 常数 K 可以从标准样品测量得到。已知 25℃的水 T2=2.3S，所以对于水样品 K =− − ( ) ⎡ ⎣ ⎢ ⎤ ⎦ ⎥⋅ − ln . 2 2 2 3 1 2 1 2 3 1 3 τ τ τ τ 思考题 试用矢量模型分析 M 在 180°-τ-90°脉冲作用下的运动情况

实验7-3 光磁共振 光磁共振，亦称光泵(Optical Pumping)。这个实验方法是由法国物理学家Kastler在 1950年首创的。它的基本思想是利用光的抽运效应造成原子基态Zeeman能级上粒子布居 的偏极化，即偏离热平衡时所遵循的Boltzmann分布。然后利用磁共振效应对这种偏极化布 居进行扰动，使光的抽运速率变化。通过对抽运速率变化的探测来研究原子Zeeman能级的 结构（超精细结构-hyperfine)。 光磁共振实验巧妙地利用了光探测的高灵敏度和磁共振的高分辨率，在实验构思上堪 称典范。光磁共振实际上是一种双共振现象，因为抽运也是在共振下进行的。六十年代以 后在磁共振领域里双共振的实验方法得到了充分的开发，而这些双共振技术在原理上与光 磁共振则是相似的。由于光磁共振在基础物理研究、量子频标技术和弱磁场测定等方面都 有着重要的应用价值，因此Kastler获得了1966年的诺贝尔奖。 光磁共振是一个物理内容很丰富的实验。它涉及磁共振、核自旋、核磁矩等一些物理 概念：又用到光学，电磁学和电子学方面的许多实验技术。 一、 实验原理 (1)光的抽运效应 1.原子的能级和Zeeman分裂 本实验研究的对象是碱金属铷的两个同位素85Rb和87Rb。它们的丰度分别为72.15% 和27.85%。铷的基态是52S12,第一激发态是52P12和52P32·从52P12到52S12的跃迁称为 D1线，B=7948A；从5P3n到52S1n跃迁称为D2线，元=7800A。 在原子物理中我们已经知道核自旋=0的原子LS耦合后的总角动量P,和原子总磁矩 之间的关系为 ,=-8月 (7-3-1) 8=1+J+)L(L+1)+SS+) (7-3-2) 2J(J+) ≠0时还要进一步考虑电子的总角动量与核的总角动量之间的耦合，一般地有： Pe=币，+) (7-3-3) e Pr HF =-8F 2mc (7-3-4) 180

180 实验 7-3 光磁共振 光磁共振，亦称光泵（Optical Pumping）。这个实验方法是由法国物理学家 Kastler 在 1950 年首创的。它的基本思想是利用光的抽运效应造成原子基态 Zeeman 能级上粒子布居 的偏极化，即偏离热平衡时所遵循的 Boltzmann 分布。然后利用磁共振效应对这种偏极化布 居进行扰动，使光的抽运速率变化。通过对抽运速率变化的探测来研究原子 Zeeman 能级的 结构（超精细结构--hyperfine）。 光磁共振实验巧妙地利用了光探测的高灵敏度和磁共振的高分辨率，在实验构思上堪 称典范。光磁共振实际上是一种双共振现象，因为抽运也是在共振下进行的。六十年代以 后在磁共振领域里双共振的实验方法得到了充分的开发，而这些双共振技术在原理上与光 磁共振则是相似的。由于光磁共振在基础物理研究、量子频标技术和弱磁场测定等方面都 有着重要的应用价值，因此 Kastler 获得了 1966 年的诺贝尔奖。 光磁共振是一个物理内容很丰富的实验。它涉及磁共振、核自旋、核磁矩等一些物理 概念；又用到光学，电磁学和电子学方面的许多实验技术。 一、 实验原理 （1） 光的抽运效应 1．原子的能级和 Zeeman 分裂 本实验研究的对象是碱金属铷的两个同位素 85Rb 和 87Rb。它们的丰度分别为 72.15％ 和 27.85％。铷的基态是 52 S1/2，第一激发态是 52 P1/2 和 52 P3/2·从 52 P1/2 到 52 S1/2 的跃迁称为 D1 线，λ D1 =7948A o ；从 52 P3/2 到 52 S1/2 跃迁称为 D2 线， λ D2 =7800A o 。 在原子物理中我们已经知道核自旋 I=0 的原子 LS 耦合后的总角动量 K PJ 和原子总磁矩 之间的关系为 K K μ JJ J g e mc = − P 2 （7-3-1） ( ) g JJ LL SS J J J = + + 1 1 1 2 1 ( + ) - ( + 1) + ( + ) （7-3-2） I≠0 时还要进一步考虑电子的总角动量与核的总角动量之间的耦合，一般地有： K K K P PP F IJ = + （7-3-3） K K μ FF F g e mc = − P 2 （7-3-4）

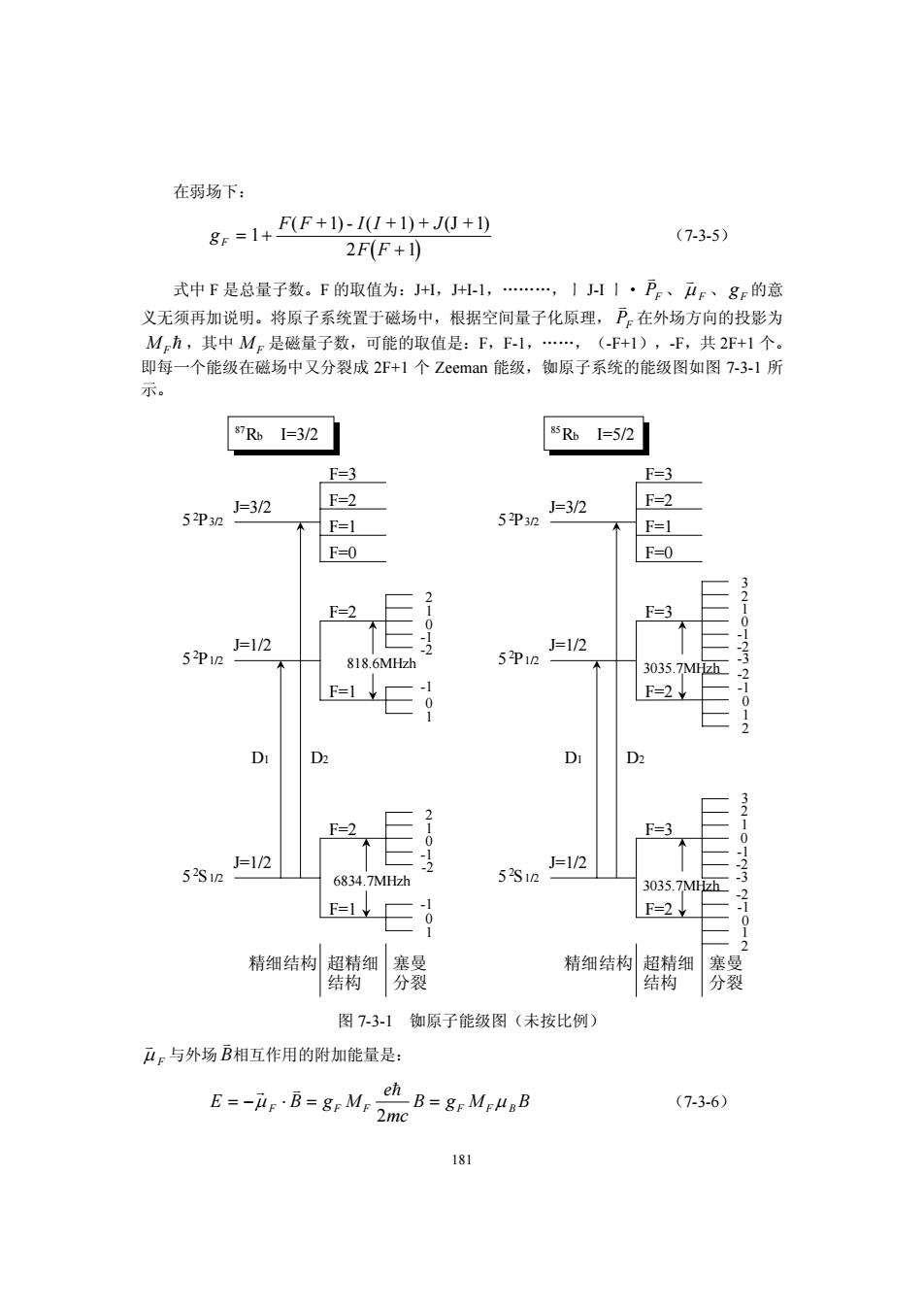
在弱场下： 8e=1+FF+0-1W+1)+J0+D (7-3-5) 2F(F+1) 式中F是总量子数。下的取值为：JHH,J+l,…,1JH1·万、4F、gF的意 义无须再加说明。将原子系统置于磁场中，根据空间量子化原理，P。在外场方向的投影为 M方，其中Me是磁量子数，可能的取值是：F,F-1,…,(-F+1),-F,共2F+1个。 即每一个能级在磁场中又分裂成2F+1个Zeeman能级，铷原子系统的能级图如图7-3-1所 示。 87RbI=3/2 85RbI=5/2 F=3 F=3 J=3/2 F=2 J=3/2 F=2 52P32 F=1 5P32 F=1 F=0 F=0 3 2 F=2 F=3 0 0 J=1/2 J=1/2 52P12 818.6MHzh 52P12 3 3035.7MHzh -2 F=2 0 D2 DI D2 3 2 F=2 F=3 0 0 、 J=1/2 52S12 -2 J=1/2 6834.7MHzh 52S12 3 3035.7Mzh -2 F=1￥ -1 二 0 F=2 0 2 精细结构 超精细 塞 精细结构 超精细 塞曼 结构 分裂 结构 分裂 图7-3-1铷原子能级图（未按比例） 4。与外场B相互作用的附加能量是： gM h gM (7-3-6) 181

181 在弱场下： ( ) g FF II J F F F = + + 1 1 1 2 1 ( + ) - ( +1) + (J + ) （7-3-5） 式中 F 是总量子数。F 的取值为：J+I，J+I-1，………，ㄧ J-I ㄧ· K PF 、 K μ F 、 gF 的意 义无须再加说明。将原子系统置于磁场中，根据空间量子化原理， K PF 在外场方向的投影为 MF = ，其中 MF 是磁量子数，可能的取值是：F，F-1，……，（-F+1），-F，共 2F+1 个。 即每一个能级在磁场中又分裂成 2F+1 个 Zeeman 能级，铷原子系统的能级图如图 7-3-1 所 示。 K μ F 与外场 K B相互作用的附加能量是： E B gM e mc =− ⋅ = = F F F F FB B gM B G K = μ μ 2 （7-3-6） 5 P1/2 2 5 P3/2 2 5 S1/2 2 5 S1/2 2 5 P1/2 2 5 P3/2 2 Rb 85 Rb I=5/2 87 I=3/2 J=3/2 J=1/2 J=1/2 D1 D2 精细结构 超精细 结构 塞曼 分裂 F=2 F=1 F=0 F=3 -2 J=3/2 J=1/2 J=1/2 F=1 F=2 F=1 F=2 D1 D2 6834.7MHzh 818.6MHzh 精细结构 超精细 结构 塞曼 分裂 F=2 F=1 F=0 F=3 2 1 0 -1 -2 -1 0 1 -1 0 1 2 1 0 -1 -2 F=2 F=3 3035.7MHzh 2 1 0 -1 -2 3 -3 2 1 0 -1 -2 F=2 F=3 3035.7MHzh 2 1 0 -1 -2 3 -3 2 1 0 -1 图 7-3-1 铷原子能级图（未按比例）

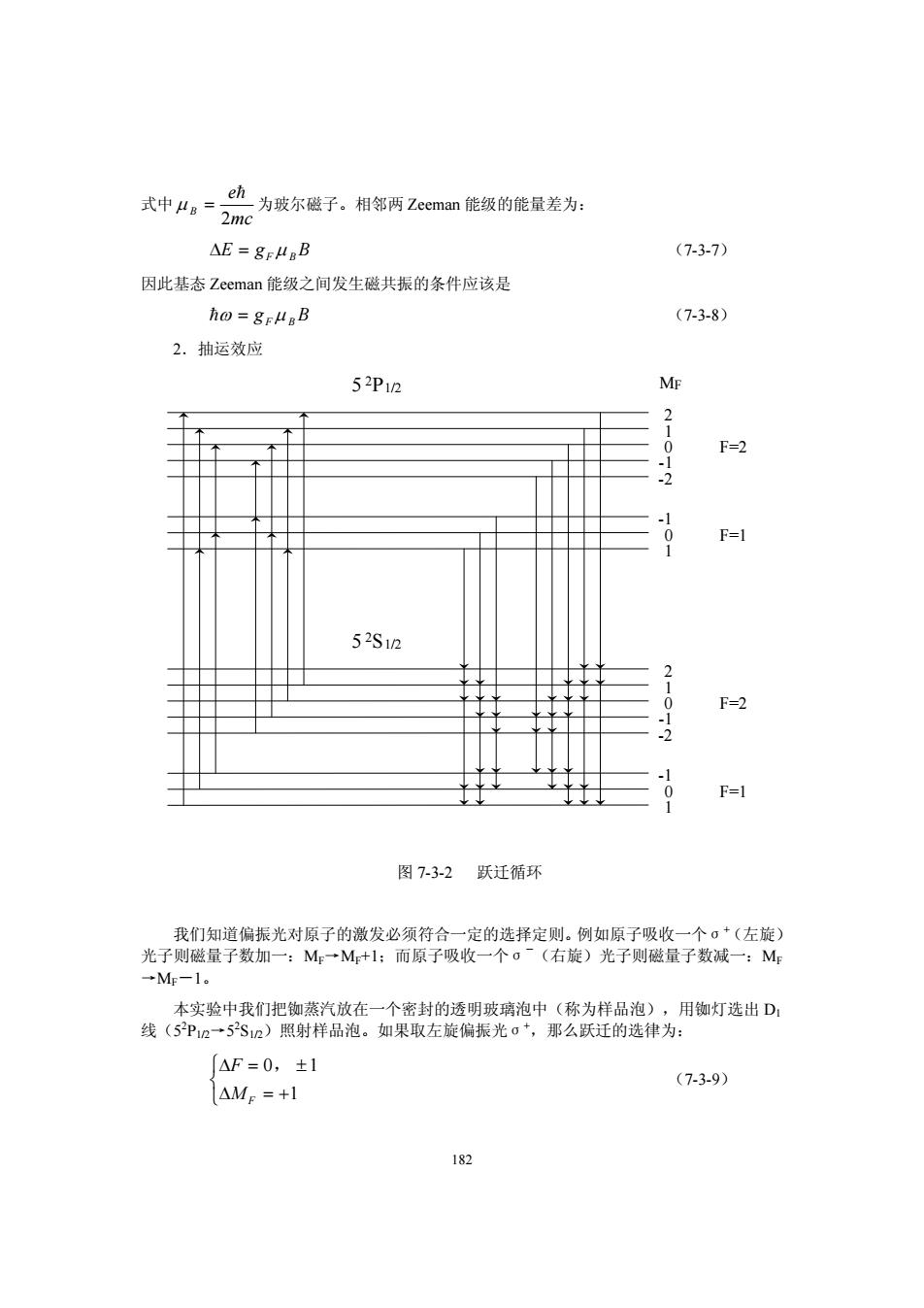
eh为玻尔磁子。相邻两Zeeman能级的能量差为： 式中μg=2mc △E=gE4BB (7-3-7) 因此基态Zeeman能级之间发生磁共振的条件应该是 ho=gFμgB (7-3-8) 2.抽运效应 52P12 MF 210 F=2 -1 0 F=1 52S12 210 F=2 2 0 F=1 图7-3-2跃迁循环 我们知道偏振光对原子的激发必须符合一定的选择定则。例如原子吸收一个σ+（左旋） 光子则磁量子数加一：M→M+1;而原子吸收一个oˉ（右旋）光子则磁量子数减一：M →Mr-1。 本实验中我们把铷蒸汽放在一个密封的透明玻璃泡中（称为样品泡），用铷灯选出D1 线(5P12→52S12)照射样品泡。如果取左旋偏振光o+,那么跃迁的选律为： △F=0,±1 (7-3-9) △ME=+1 182

182 式中 μ B e mc = = 2 为玻尔磁子。相邻两 Zeeman 能级的能量差为： ΔEg B = F B μ （7-3-7） 因此基态 Zeeman 能级之间发生磁共振的条件应该是 =ω = g B F B μ （7-3-8） 2．抽运效应 我们知道偏振光对原子的激发必须符合一定的选择定则。例如原子吸收一个σ+ （左旋） 光子则磁量子数加一：MF→MF+1；而原子吸收一个σ－ （右旋）光子则磁量子数减一：MF →MF－1。 本实验中我们把铷蒸汽放在一个密封的透明玻璃泡中（称为样品泡），用铷灯选出 D1 线（52 P1/2→52 S1/2）照射样品泡。如果取左旋偏振光σ+ ，那么跃迁的选律为： Δ Δ F MF = ± = + ⎧ ⎨ ⎩ 0 1 1 ， （7-3-9） 2 1 0 -1 -2 1 0 -1 2 1 0 -1 -2 1 0 -1 5 P1/2 MF 2 5 S1/2 2 F=2 F=1 F=2 F=1 图 7-3-2 跃迁循环