
Instruction Manual and Experiment Guide FOURIER SYNTHESIZER 中o 中! 回 回 回 团 Shanghai JiaoTong University Center of Physics Experiment
Instruction Manual and Experiment Guide FOURIER SYNTHESIZER Shanghai JiaoTong University Center of Physics Experiment

Table of contents Section Page Experiment 1:Adding Sine Waves ofthe Same Frequency.............. Experiment2:Adding Sine Waves ofDifferent Frequency............2 Experiment3:Fourier Synthesis............... 3 Experiment4:Gibbs Phenomenon.......................... 5 Experiment 5:Music...... …6 Experiment 6:Lissajous Figures..... P Experiment 7:Interesting Traces...... 9
Table of contents Section Page Experiment 1: Adding Sine Waves of the Same Frequency.…….…..1 Experiment 2: AddingSine Waves of Different Frequency…………2 Experiment 3: Fourier Synthesis…………………………………….3 Experiment 4: Gibbs Phenomenon…………………………………..5 Experiment 5: Music………………………………………………...6 Experiment 6: Lissajous Figures…………………………………….8 Experiment 7: Interesting Traces…………………………………….9

Experiment 1:Adding Sine Waves of the Same Frequency Introduction There are standard trigonometric identities that can be used to mathematically add sine waves and cosine waves.You can then graph the resulting waveform to determine exactly what the sum of the two waves would look like.Although a physicist needs to be able to use such mathematical tools,it's important to have an intuitive grasp of what is happening when trigonometric functions are added. Procedure NOTE:This procedure assumes you are using an oscilloscope with an external trigger 1.Hook up the Fourier Synthesizer to your oscilloscope as described in the SETUP section. Connect the oscilloscope input to the 10kQ output connector if the summing amplifier.Trigger the oscilloscope from the TRIGGER output. 2.Switch the first fundamental signal SUMMING AMPLIFIER switch to the in position.Make sure the second fundamental and all harmonics are switched OUT.Select the SINE wave output signal option.Adjust the AMPLITUDE control to a convenient value near maximum amplitude,(IV peak is usually convenient).Adjust the vertical scaling in the oscilloscope so that the peak of the sine wave is less than or equal to half of the maximum display on the scope,(0.SV/div is usually convenient).Adjust the 0-90 and 0-180 switches and the VARIABLE PHASE control to display either a sine or cosine waveform.Switch the first fundamental signal OUT and the second fundamental signal IN.Adjust the controls for the second fundamental to produce a sine wave signal identical in amplitude and phase to the first fundamental signal. 3.Now switch the first fundamental signal (IN to the summing Amplifier.Is the combined waveform a sine wave?How does its amplitude and phase compare with the amplitudes and phases of the two original sine waves? 4.Vary the amplitude of one of the fundamentals and examine the amplitude and phase of the combined wave. 5.Vary the phase of one of the fundamentals,first with the variable phase control,then with the 0-90 and 0-180 switches.Examine the amplitude and phase of the combined wave. 6.What conditions produce,a combined waveform with a maximum amplitude?A minimum amplitude? 7.Repeat the above procedure with two triangular waves and then two square waves. NOTE:The VANIABLE PHASE control has no effect on the triangle and square wave outputs. The phase of these wave forms can only be shifted 90"or 180 using the 0-90"and 0-180" switches. Then try adding a square wave to a sine wave,a square wave to a triangular wave,and a sine wave to a triangular wave.In each case,first examine the constituent waves,then try to sketch what you believe the combined waveform will look like.Then add the two waves together to see how accurate your sketch was
1 Experiment 1: Adding Sine Waves of the Same Frequency Introduction There are standard trigonometric identities that can be used to mathematically add sine waves and cosine waves. You can then graph the resulting waveform to determine exactly what the sum of the two waves would look like. Although a physicist needs to be able to use such mathematical tools, it's important to have an intuitive grasp of what is happening when trigonometric functions are added. Procedure NOTE: This procedure assumes you are using an oscilloscope with an external trigger. 1. Hook up the Fourier Synthesizer to your oscilloscope as described in the SETUP section. Connect the oscilloscope input to the 10kQ output connector if the summing amplifier. Trigger the oscilloscope from the TRIGGER output. 2. Switch the first fundamental signal SUMMING AMPLIFIER switch to the in position. Make sure the second fundamental and all harmonics are switched OUT. Select the SINE wave output signal option. Adjust the AMPLITUDE control to a convenient value near maximum amplitude, (IV peak is usually convenient). Adjust the vertical scaling in the oscilloscope so that the peak of the sine wave is less than or equal to half of the maximum display on the scope, (0.SV/div is usually convenient). Adjust the 0-90 and 0-l80 switches and the VARIABLE PHASE control to display either a sine or cosine waveform. Switch the first fundamental signal OUT and the second fundamental signal IN. Adjust the controls for the second fundamental to produce a sine wave signal identical in amplitude and phase to the first fundamental signal. 3. Now switch the first fundamental signal (IN to the summing Amplifier. Is the combined waveform a sine wave? How does its amplitude and phase compare with the amplitudes and phases of the two original sine waves? 4. Vary the amplitude of one of the fundamentals and examine the amplitude and phase of the combined wave. 5. Vary the phase of one of the fundamentals, first with the variable phase control, then with the 0-90° and 0-180°switches. Examine the amplitude and phase of the combined wave. 6. What conditions produce, a combined waveform with a maximum amplitude? A minimum amplitude? 7. Repeat the above procedure with two triangular waves and then two square waves. NOTE: The VANIABLE PHASE control has no effect on the triangle and square wave outputs. The phase of these wave forms can only be shifted 90" or 180` using the 0-90" and 0-180" switches. Then try adding a square wave to a sine wave, a square wave to a triangular wave, and a sine wave to a triangular wave. In each case, first examine the constituent waves, then try to sketch what you believe the combined waveform will look like. Then add the two waves together to see how accurate your sketch was

Experiment 2:Adding Sine Waves of Different Frequency Introduction Two sine wave of the same amplitude and phase can be added mathematically using the formula: sin(2 t)+sin(2mv2t)=2cosa(v -v2 )tsin a(v +v2 )t If v and v,are greatly different,then the wave described by the right side of this equation is even more difficult to visualize than the wave described by the left side. However of v and v,are nearly the same,the cosine term will have a much lower frequency than the sine term.Then the wave can be visualized as a sine wave of frequency,with the amplitude of this sine wave varying slowly with a frequency of(v -v,)/2. If this were a sound wave,you would hear what is called beats,the relatively slow pulsing of the tone as the amplitude rises and falls. Procedure NOTE: a.This procedure assumes you are using a dual trace scope with an external trigger. b.A speaker output,in addition to the oscilloscope,is a valuable addition to this lab 1.Hook up the Fourier Synthesizer to your oscilloscope as described in the SETUP section. Connect one of the oscilloscope inputs to the 10k Output connector of the 9th harmonic. Connect the other oscilloscope input to the 10k Output connector of the summed waveform. 2.Switch the 8th harmonic into the summing amplifier.Make sure all the other waveforms are switched out.Examine the 8th and 9th hammonics at the same time.Adjust their amplitudes and phases to the same values. 3.Now add the two waves by switching the 9th harmonic into the summing amplifier(be sure to flip the 0-180 switch at the same time to offset the 180"phase shift caused by the summing amplifier).Describe the resulting waveform.Do you see beats,If so,what is the frequency of the beats?What is the frequency of the modulated wave? 4.Describe what happens as you vary the amplitude or phase ofeither harmonic. 5.Repeat the above steps using different combinations of harmonics,such as the 7th and the 8th, the 7th and the 9th,the,Ist and the 2nd,the 2nd and the 9th.Try any combinations that you think might be interesting.In each case,describe your results.Is the resulting waveform periodic?If so,what is the period?Do beats occur? 6.From your observations,what generalizations can you make about adding sine waves of different frequencies?Under what conditions do you expect beats?
2 Experiment 2: Adding Sine Waves of Different Frequency Introduction Two sine wave of the same amplitude and phase can be added mathematically using the formula: sin( 2 v t) sin( 2 v t) 2cos (v v )tsin (v v )t 1 + 2 = 1 − 2 1 + 2 If v 1 and v 2 are greatly different, then the wave described by the right side of this equation is even more difficult to visualize than the wave described by the left side. However of v 1 and v 2 are nearly the same, the cosine term will have a much lower frequency than the sine term. Then the wave can be visualized as a sine wave of frequency, with the amplitude of this sine wave varying slowly with a frequency of (v 1 -v 2 )/2. If this were a sound wave, you would hear what is called beats, the relatively slow pulsing of the tone as the amplitude rises and falls. Procedure NOTE: a. This procedure assumes you are using a dual trace scope with an external trigger. b. A speaker output, in addition to the oscilloscope, is a valuable addition to this lab. 1. Hook up the Fourier Synthesizer to your oscilloscope as described in the SETUP section. Connect one of the oscilloscope inputs to the 10kΩ Output connector of the 9th harmonic. Connect the other oscilloscope input to the 10kΩ Output connector of the summed waveform. 2. Switch the 8th harmonic into the summing amplifier. Make sure all the other waveforms are switched out. Examine the 8th and 9th harmonics at the same time. Adjust their amplitudes and phases to the same values. 3. Now add the two waves by switching the 9th harmonic into the summing amplifier (be sure to flip the 0-180 switch at the same time to offset the 180" phase shift caused by the summing amplifier). Describe the resulting waveform. Do you see beats, If so, what is the frequency of the beats? What is the frequency of the modulated wave? 4. Describe what happens as you vary the amplitude or phase of either harmonic. 5. Repeat the above steps using different combinations of harmonics, such as the 7th and the 8th, the 7th and the 9th, the, 1st and the 2nd, the 2nd and the 9th. Try any combinations that you think might be interesting. In each case, describe your results. Is the resulting waveform periodic? If so, what is the period? Do beats occur? 6. From your observations, what generalizations can you make about adding sine waves of different frequencies? Under what conditions do you expect beats?

Experiment 3:Fourier Synthesis Introduction Joseph Fourier discovered that any periodic function can be expressed as an infinite sum,or series, of sine and cosine functions.In such an infinite series,each term is a harmonic of some fundamental frequency.That is to say,the frequency of each term is an integer times some constant frequency. The Fourier Series is one of many reasons why harmonic motion is so important in physics and technology.Using Fourier analysis,any periodic motion can be understood as a superposition of harmonic motions.Since harmonic motion is well understood,this offers a powerful approach to studying a large variety of phenomena. In this experiment,you will have a chance to see how several different waveforms can be built up ("synthesized")by adding sine or cosine waveforms. Procedure 1.Hook up the Fourier Synthesizer to your oscilloscope as described in the SETUP section. 2.Connect the oscilloscope input to the 10k Q Output connector of the summing amplifier.If you are using a dual trace scope,you can use the other trace to examine the harmonic waveforms,before you add them in to the combined waveform. 3.Zero the Synthesizer.That is,set the phase of all the harmonics to zero. 4.Create a square wave as follows: a.Switch the fundamental into the summing amplifier(flip the SUMMING AMPLIFIER switch to IN).Adjust the amplifier as high as it will go and adjust the horizontal position of the trace so the wave looks like a cosine function b.Switch out the fundamental and switch in the 3rd harmonic.Adjust its amplitude to 1/3 the amplitude of the fundamental.Shift its phase by 1800 so that it looks'like a minus cosine function. c.Switch out the 3rd harmonic and switch in the 5th harmonic.Adjust its amplitude to 1/5 that of the fundamental.The phase should be the same as the fundamental. d.Switch out the 5th harmonic and switch in the 7th harmonic.Adjust its amplitude to 1/7 the amplitude of the fundamental.Shift its phase by 180"so that it looks like a minus cosine function. e.Switch out the 7th harmonic and switch in the 5th harmonic.Adjust its amplitude to 1/9 that of the fundamental.The phase should be the same as the fundamental. f.Now switch all the harmonics you have just adjusted into the summing amplifier.Observe how each harmonic adds to the square waveform.Of course,to get a perfect square wave, you would have to add an infinite number of harmonics,following this same pattern. NOTE:You can often improve your final waveform by making small adjustments to the phase angles(the Variable Phase controls are very sensitive and may not perfectly zeroed when you start).Start over building the wave.Begin with the fundamental.Then add the 3rd harmonic and adjust its phase until the combined waveform is perfectly symmetrical.Add each successive harmonic,each time adjusting the phase until the waveform is perfectly symmetrical.The accuracy of the waveform also depends on how closely the amplitude of each harmonic fits the specification given above
3 Experiment 3: Fourier Synthesis Introduction Joseph Fourier discovered that any periodic function can be expressed as an infinite sum, or series, of sine and cosine functions. In such an infinite series, each term is a harmonic of some fundamental frequency. That is to say, the frequency of each term is an integer times some constant frequency. The Fourier Series is one of many reasons why harmonic motion is so important in physics and technology. Using Fourier analysis, any periodic motion can be understood as a superposition of harmonic motions. Since harmonic motion is well understood, this offers a powerful approach to studying a large variety of phenomena. In this experiment, you will have a chance to see how several different waveforms can be built up ("synthesized") by adding sine or cosine waveforms. Procedure 1. Hook up the Fourier Synthesizer to your oscilloscope as described in the SETUP section. 2. Connect the oscilloscope input to the 10kΩ Output connector of the summing amplifier. If you are using a dual trace scope, you can use the other trace to examine the harmonic waveforms, before you add them in to the combined waveform. 3. Zero the Synthesizer. That is, set the phase of all the harmonics to zero. 4. Create a square wave as follows: a. Switch the fundamental into the summing amplifier (flip the SUMMING AMPLIFIER switch to IN). Adjust the amplifier as high as it will go and adjust the horizontal position of the trace so the wave looks like a cosine function b. Switch out the fundamental and switch in the 3rd harmonic. Adjust its amplitude to l/3 the amplitude of the fundamental. Shift its phase by 180o so that it looks` like a minus cosine function. c. Switch out the 3rd harmonic and switch in the 5th harmonic. Adjust its amplitude to l/5 that of the fundamental. The phase should be the same as the fundamental. d. Switch out the 5th harmonic and switch in the 7th harmonic. Adjust its amplitude to l/7 the amplitude of the fundamental. Shift its phase by 180" so that it looks like a minus cosine function. e. Switch out the 7th harmonic and switch in the 5th harmonic. Adjust its amplitude to 1/9 that of the fundamental. The phase should be the same as the fundamental. f. Now switch all the harmonics you have just adjusted into the summing amplifier. Observe how each harmonic adds to the square waveform. Of course, to get a perfect square wave, you would have to add an infinite number of harmonics, following this same pattern. NOTE:You can often improve your final waveform by making small adjustments to the phase angles(the Variable Phase controls are very sensitive and may not perfectly zeroed when you start).Start over building the wave. Begin with the fundamental. Then add the 3rd harmonic and adjust its phase until the combined waveform is perfectly symmetrical. Add each successive harmonic, each time adjusting the phase until the waveform is perfectly symmetrical. The accuracy of the waveform also depends on how closely the amplitude of each harmonic fits the specification given above
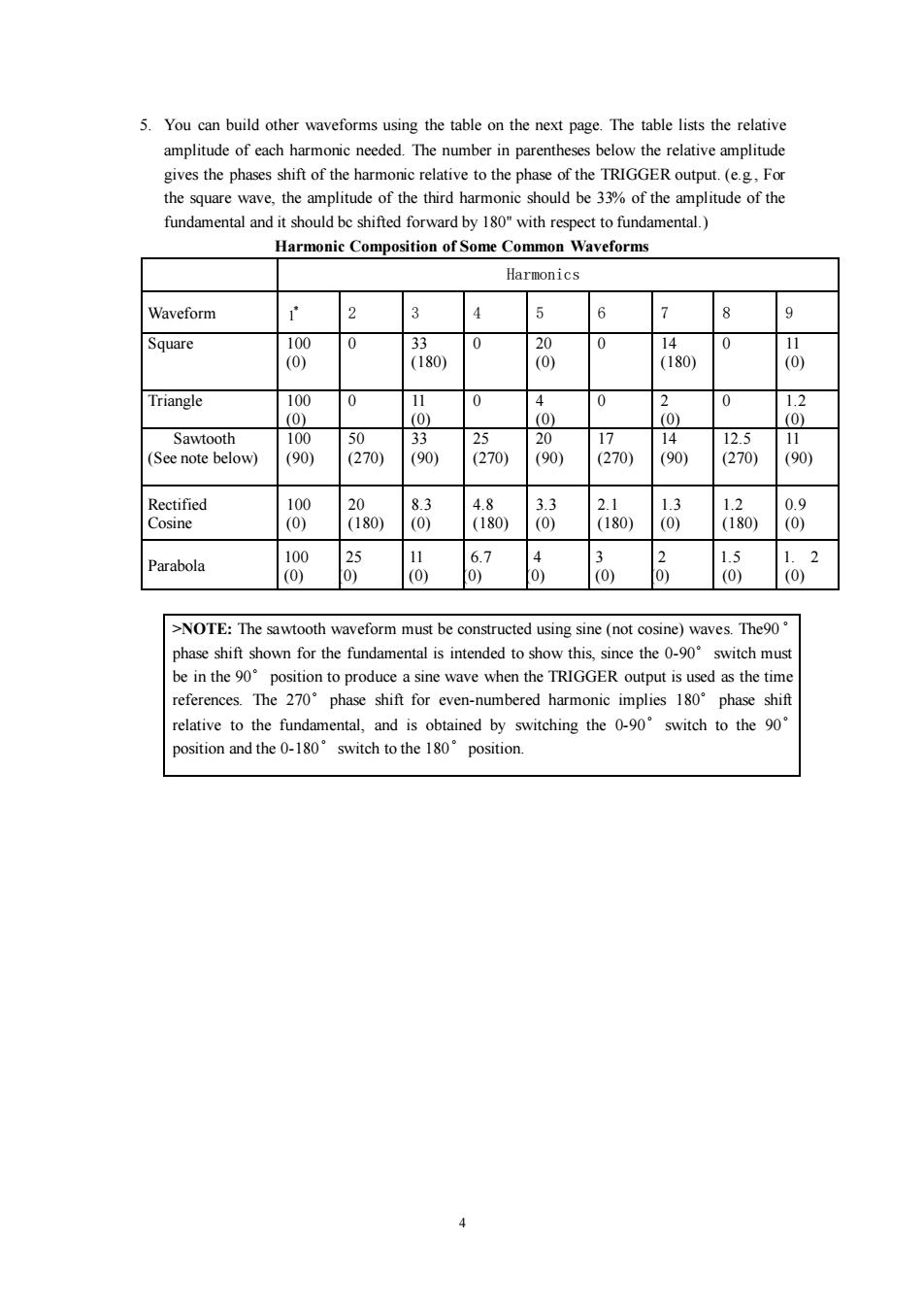
5.You can build other waveforms using the table on the next page.The table lists the relative amplitude of each harmonic needed.The number in parentheses below the relative amplitude gives the phases shift of the harmonic relative to the phase of the TRIGGER output.(e.g,For the square wave,the amplitude of the third harmonic should be 33%of the amplitude of the fundamental and it should bc shifted forward by 180"with respect to fundamental.) Harmonic Composition of Some Common Waveforms Harmonics Waveform 2 4 5 6 7 8 9 Square 100 0 33 0 20 0 14 0 11 (0) (180) (0) (180) (0) Triangle 100 0 11 4 0 2 0 1.2 (0) (0) (0) (0) (0) Sawtooth 100 50 33 25 20 17 14 12.5 11 (See note below) (90) (270) (90) (270) (90) (270) (90) (270) (90) Rectified 100 20 8.3 4.8 3.3 2.1 1.3 1.2 0.9 Cosine (0) (180) (0) (180) (0) (180) (0) (180) (0) Parabola 100 25 11 6.7 4 2 1.5 2 (0) 0) (0) 0) 0) (0) 0) (0) (0) >NOTE:The sawtooth waveform must be constructed using sine(not cosine)waves.The90 phase shift shown for the fundamental is intended to show this,since the 0-90 switch must be in the 90 position to produce a sine wave when the TRIGGER output is used as the time references.The 270 phase shift for even-numbered harmonic implies 180phase shift relative to the fundamental,and is obtained by switching the 0-90switch to the 90' position and the 0-180 switch to the 180 position
4 5. You can build other waveforms using the table on the next page. The table lists the relative amplitude of each harmonic needed. The number in parentheses below the relative amplitude gives the phases shift of the harmonic relative to the phase of the TRIGGER output. (e.g., For the square wave, the amplitude of the third harmonic should be 33% of the amplitude of the fundamental and it should bc shifted forward by 180" with respect to fundamental.) Harmonic Composition of Some Common Waveforms Harmonics Waveform * 1 2 3 4 5 6 7 8 9 Square 100 (0) 0 33 (180) 0 20 (0) 0 14 (180) 0 11 (0) Triangle 100 (0) 0 11 (0) 0 4 (0) 0 2 (0) 0 1.2 (0) Sawtooth (See note below) 100 (90) 50 (270) 33 (90) 25 (270) 20 (90) 17 (270) 14 (90) 12.5 (270) 11 (90) Rectified Cosine 100 (0) 20 (180) 8.3 (0) 4.8 (180) 3.3 (0) 2.1 (180) 1.3 (0) 1.2 (180) 0.9 (0) Parabola 100 (0) 25 (0) 11 (0) 6.7 (0) 4 (0) 3 (0) 2 (0) 1.5 (0) 1. 2 (0) >NOTE: The sawtooth waveform must be constructed using sine (not cosine) waves. The90 phase shift shown for the fundamental is intended to show this, since the 0-90 switch must be in the 90 position to produce a sine wave when the TRIGGER output is used as the time references. The 270 phase shift for even-numbered harmonic implies 180 phase shift relative to the fundamental, and is obtained by switching the 0-90 switch to the 90 position and the 0-180 switch to the 180 position

Experiment 4:Gibbs Phenomenon Introduction In Fourier Synthesis,adding successive harmonics brings the waveform,closer and closer to the desired shape.However,you'll find that the synthesizer has most difficulty in producing sharp discontinuities in a waveform,such as the instantaneous drop or rise at the corners of a square wave.This is true in Fourier Synthesis in general,and is known as Gibbs Phenomenon.At these discontinuities in the waveform there is generally an overshoot as harmonics are added,as of the harmonics are trying to make the corner,but always go a bit too far before they can get turned around.Gibbs demonstrated that the amount of overshoot does not depend on the number of harmonics used,but the width of each overshoot peak becomes narrower as the number increases. With an infinite number of harmonics,of course,the sum of the harmonics exactly reproduces the waveform.Unfortunately,that's a little tough to demonstrate. Procedure Repeat the procedure of Experiment 3 for building a square wave or other waveform. As each harmonic is added,measure the amount of overshoot and the width of the overshoot peaks
5 Experiment 4: Gibbs Phenomenon Introduction In Fourier Synthesis, adding successive harmonics brings the waveform, closer and closer to the desired shape. However, you'll find that the synthesizer has most difficulty in producing sharp discontinuities in a waveform, such as the instantaneous drop or rise at the corners of a square wave. This is true in Fourier Synthesis in general, and is known as Gibbs Phenomenon. At these discontinuities in the waveform there is generally an overshoot as harmonics are added, as of the harmonics are trying to make the corner, but always go a bit too far before they can get turned around. Gibbs demonstrated that the amount of overshoot does not depend on the number of harmonics used, but the width of each overshoot peak becomes narrower as the number increases. With an infinite number of harmonics, of course, the sum of the harmonics exactly reproduces the waveform. Unfortunately, that's a little tough to demonstrate. Procedure Repeat the procedure of Experiment 3 for building a square wave or other waveform. As each harmonic is added, measure the amount of overshoot and the width of the overshoot peaks

Experiment 5:Music Introduction The tones produced by periodic waveforms are example of complex periodic waves.Musicians generally use three terms to describe a musical tone-pitch,loudness,and quality.Pitch refers to the frequency of vibration of the tone.A higher frequency produces a higher pitch.Loudness refers to the amplitude of the sound wave,or to be more precise,to our subjective sense of that amplitude. Quality is a more complicated phenomena.Two instruments,such as a clarinet and a piano,can produce tones of the same pitch and loudness,yet the two tones will be quite distinct.The reason for this is that virtually all musical tones are made up of a relatively high amplitude fundamental frequency,which determines the pitch,and a variety of higher harmonies at lower amplitudes, which determine the quality of the tone.It is these higher frequencies and their relative amplitudes that let us distinguish the same tone as it is played by different instruments. In this experiment,you will examine the relationships between wave shape,as seen on the oscilloscope,and the sound produced when the wave drives a speaker. Procedure 1.Hook up the Fourier Synthesizer to your oscilloscope as described in the SETUP section. 2.Connect a speaker (82 input impedance)between the 89 OUTPUT connectors of the Synthesizer. 3.Turn on the Synthesizer and switch the first fundamental into the summing amplifier.Adjust the amplitude of the wave until it is a convenient size on the oscilloscope.You can adjust the volume of the sound with the GAIN knob on the Synthesizer. 4.Switch the waveform to a square wave and readjust the amplitude to equal that of the sine wave.Now switch to a triangular wave.Switch back and forth between these three waveforms. Describe any differences you notice in the pitch,loudness,and quality of the three tones.Try to relate the differences you hear to differences in the waveforms you see on the oscilloscope. 5.Switch the waveform of the fundamental back to a sine wave.Switch in the 2nd harmonic Vary its amplitude and note the effects on the scope and on the sound.Set the amplitude of the fundamental and the 2nd harmonic to the same level.Does one tone or the other seen to dominate?(i.e.do you hear a single tone that varies in quality as you adjust the amplitude of either harmonic,or do you hear two tones of different pitch?)Change the phase of the 2nd harmonic.Does changing the phase affect the sound? 6.Switch in higher harmonic.Vary the amplitude and again,try to relate the pitch,loudness,and quality of the sound to the waveform you sec on the oscilloscope. 7.The table below show a the harmonic make up of the tones from a violin,a clarinet,and a piano.I'ry each tone.Adjust each individual harmonic to the proper amplitude,then switch them all into the summing amplifier to produce the tone. NOTE:The tones produced by the Fourier Synthesizer will not sound exactly like the chosen musical instrument.Several other factors play a role.One factor is that higher harmonic may be needed to more closely produce the tone.Another is that most musical instruments do not produce a continuous tone such as those of the synthesizer.The shape of the waveform produced by an instrument varies with time for each note.These variations are not reproduced by the Synthesizer. 6
6 Experiment 5: Music Introduction The tones produced by periodic waveforms are example of complex periodic waves. Musicians generally use three terms to describe a musical tone-pitch, loudness, and quality. Pitch refers to the frequency of vibration of the tone. A higher frequency produces a higher pitch. Loudness refers to the amplitude of the sound wave, or to be more precise, to our subjective sense of that amplitude. Quality is a more complicated phenomena. Two instruments, such as a clarinet and a piano, can produce tones of the same pitch and loudness, yet the two tones will be quite distinct. The reason for this is that virtually all musical tones are made up of a relatively high amplitude fundamental frequency, which determines the pitch, and a variety of higher harmonies at lower amplitudes, which determine the quality of the tone. It is these higher frequencies and their relative amplitudes that let us distinguish the same tone as it is played by different instruments. In this experiment, you will examine the relationships between wave shape, as seen on the oscilloscope, and the sound produced when the wave drives a speaker. Procedure 1. Hook up the Fourier Synthesizer to your oscilloscope as described in the SETUP section. 2. Connect a speaker (8Ω input impedance) between the 8Ω OUTPUT connectors of the Synthesizer. 3. Turn on the Synthesizer and switch the first fundamental into the summing amplifier. Adjust the amplitude of the wave until it is a convenient size on the oscilloscope. You can adjust the volume of the sound with the GAIN knob on the Synthesizer. 4. Switch the waveform to a square wave and readjust the amplitude to equal that of the sine wave. Now switch to a triangular wave. Switch back and forth between these three waveforms. Describe any differences you notice in the pitch, loudness, and quality of the three tones. Try to relate the differences you hear to differences in the waveforms you see on the oscilloscope. 5. Switch the waveform of the fundamental back to a sine wave. Switch in the 2nd harmonic. Vary its amplitude and note the effects on the scope and on the sound. Set the amplitude of the fundamental and the 2nd harmonic to the same level. Does one tone or the other seen to dominate? (i.e. do you hear a single tone that varies in quality as you adjust the amplitude of either harmonic, or do you hear two tones of different pitch?) Change the phase of the 2nd harmonic. Does changing the phase affect the sound? 6. Switch in higher harmonic. Vary the amplitude and again, try to relate the pitch, loudness, and quality of the sound to the waveform you sec on the oscilloscope. 7. The table below show a the harmonic make up of the tones from a violin, a clarinet, and a piano. 1'ry each tone. Adjust each individual harmonic to the proper amplitude, then switch them all into the summing amplifier to produce the tone. NOTE: The tones produced by the Fourier Synthesizer will not sound exactly like the chosen musical instrument. Several other factors play a role. One factor is that higher harmonic may be needed to more closely produce the tone. Another is that most musical instruments do not produce a continuous tone such as those of the synthesizer. The shape of the waveform produced by an instrument varies with time for each note. These variations are not reproduced by the Synthesizer
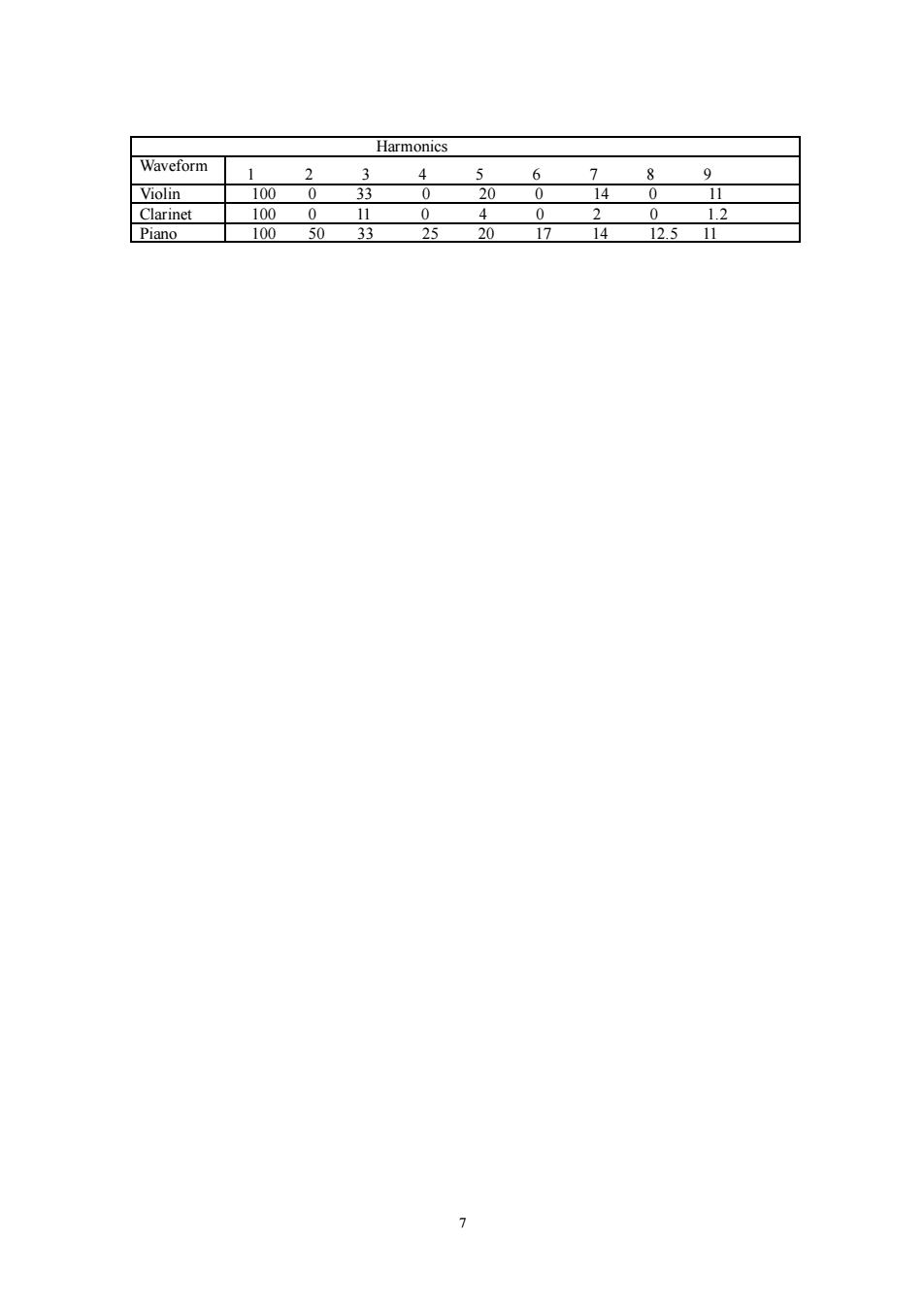
Harmonics Waveform 1 2 3 4 5 6 7 8 9 Violin 100 0 33 0 20 0 14 0 11 Clarinet 100 0 11 0 x 0 2 0 1.2 Piano 100 50 33 25 20 17 14 12.5 11 1
7 Harmonics Waveform 1 2 3 4 5 6 7 8 9 Violin 100 0 33 0 20 0 14 0 11 Clarinet 100 0 11 0 4 0 2 0 1.2 Piano 100 50 33 25 20 17 14 12.5 11

Experiment 6:Lissajous Figures Introduction Suppose a particle is traveling in harmonic motion in two dimensions,such that its equation of motion is: x=A,cos(ot+,)y=A,cos(ot+,) Since the motion of the particle in the x and y directions have the same frequency,they also have the same period,T.So,no matter where the particle is at time t,it will be back at the same point at time t+T.The path of the particle therefore,forms a closed loop. You can produce a similar sort of motion on an oscilloscope by using one waveform from the Fourier Synthesizer to control the horizontal motion of the electron beam and other waveform to control the vertical motion.Since All the waveforms of the Synthesizer are harmonics of the fundamental,the trace on the oscilloscope will always be a closed loop.These closed loops ate known as Lissajous figures,after Jules Antoine Lissajous. Procedure 1.Connect the ground jack of an oscilloscope to one of the ground jacks on the Fourier Synthesizer 2.Connect the vertical input of the scope to one of the 10k OUTPUT jack of the first fundamental. 3.Connect the horizontal input of the scope to the 10kQ OUTPUT jack of the second fundamental. 4.Adjust the amplitude and phase of the second fundamental.Then do the same with the first fundamental.Discuss how amplitude and phase variations affect the shape of the Lissajous figure.What amplitude and phase relationships are necessary to create a circular pattern? 5.Try switching one or both of the fundamentals to a square or triangular wave,Again,vary the phase and amplitude and notice the changes in the curve.Try to relate the shape of the curve with the shape of the individual waveforms. 6.Try using higher harmonics for one or both of the oscilloscope inputs.Can you make any generalizations about the shape of the curve and the harmonic used? 7.To make more complicated curves,try using the 10kQ output of the summing amplifier as one of the inputs
8 Experiment 6: Lissajous Figures Introduction Suppose a particle is traveling in harmonic motion in two dimensions, such that its equation of motion is: cos( ); x x x = A t + cos( ) y y y = A t + Since the motion of the particle in the x and y directions have the same frequency, ω they also have the same period, T. So, no matter where the particle is at time t, it will be back at the same point at time t+T. The path of the particle therefore, forms a closed loop. You can produce a similar sort of motion on an oscilloscope by using one waveform from the Fourier Synthesizer to control the horizontal motion of the electron beam and other waveform to control the vertical motion. Since All the waveforms of the Synthesizer are harmonics of the fundamental, the trace on the oscilloscope will always be a closed loop. These closed loops ate known as Lissajous figures, after Jules Antoine Lissajous. Procedure 1. Connect the ground jack of an oscilloscope to one of the ground jacks on the Fourier Synthesizer. 2. Connect the vertical input of the scope to one of the 10kΩ OUTPUT jack of the first fundamental. 3. Connect the horizontal input of the scope to the 10kQ OUTPUT jack of the second fundamental. 4. Adjust the amplitude and phase of the second fundamental. Then do the same with the first fundamental. Discuss how amplitude and phase variations affect the shape of the Lissajous figure. What amplitude and phase relationships are necessary to create a circular pattern? 5. Try switching one or both of the fundamentals to a square or triangular wave, Again, vary the phase and amplitude and notice the changes in the curve. Try to relate the shape of the curve with the shape of the individual waveforms. 6. Try using higher harmonics for one or both of the oscilloscope inputs. Can you make any generalizations about the shape of the curve and the harmonic used? 7. To make more complicated curves, try using the 10kQ output of the summing amplifier as one of the inputs