
第一章矢量分析 即数学中的“场论” 主要内容: S1.1基本概念 §1.2无旋场、无散场及矢量场的分解 §1.37算子的运算 S1.4积分定理 §1.56函数
第 章一 矢量分析 即数学中的“场论” 主要内容: §1.1 基本概念 §1.2 无旋场、无散场及矢量场的分解 §1 3. 算子的运算 §1.4 积分定理 §1.5 δ 函数

§1.1基本概念 场的定义: 一个物理量或数学量在空间的分布称为该物理量或数 学量的场。即:若对空间某一区域内的任意点,都有 某个物理量或数学量的一个确定值与之对应,则称该 区域内确定了该物理量或数学量的一个场。 数学上,场《函数(自变量为空间坐标) 标量场(Scalar Field) 场 矢量场(Vector Field) 备注:场可随时间变化,但数学中的场论仅研 究其随空间的变化
§1.1 基本概念 场的定义: 一个物理量或数学量在空间的分布称为该物理量或数 学量的场。即:若 某 域内的任意点 若对空间某一区域内的任意点,都有 某个物理量或数学量的一个确定值与之对应,则称该 区域内确定了该物理量或数学量的 个场 区域内确定了该物理量或数学量的一个场。 数学上,场 函数(自变量为空间坐标 自变量为空间坐标) 场 标量场(Scalar Field) 矢量场(Vector Field) 备注:场可随时间变化,但数学中的场论仅研 究其随空间的变化
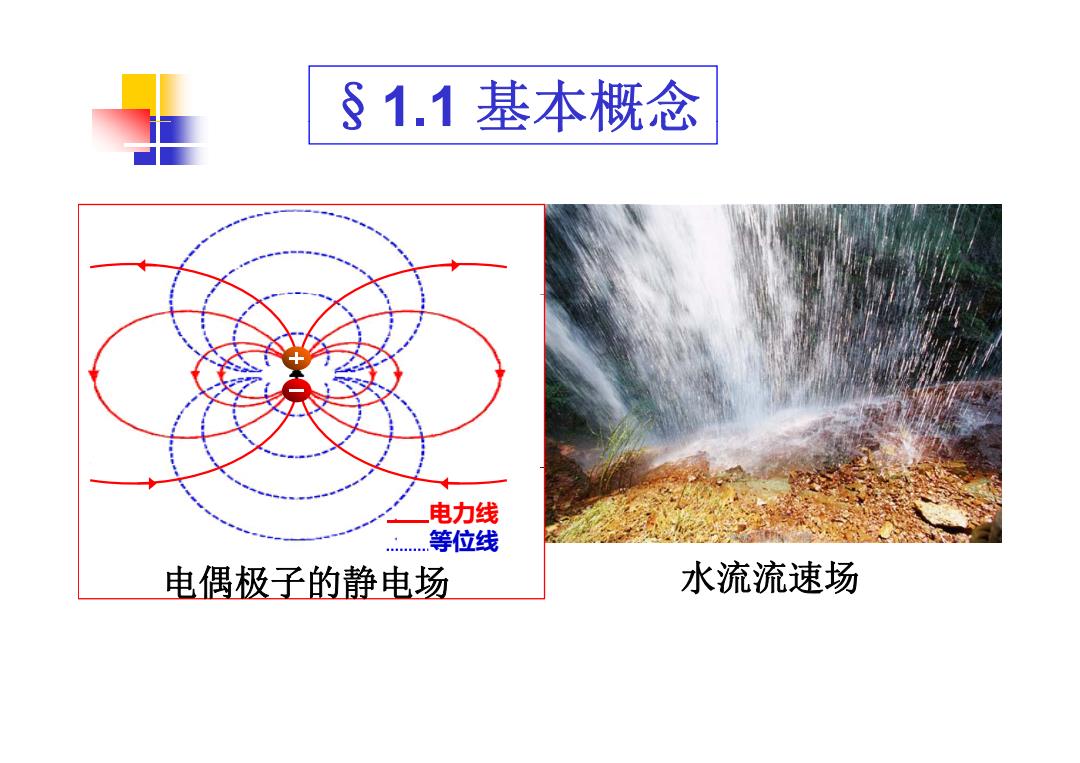
§1.1基本概念 电力线 等位线 电偶极子的静电场 水流流速场
§1.1 基本概念 等位线 电力线 电偶极子的静电场 水流流速场
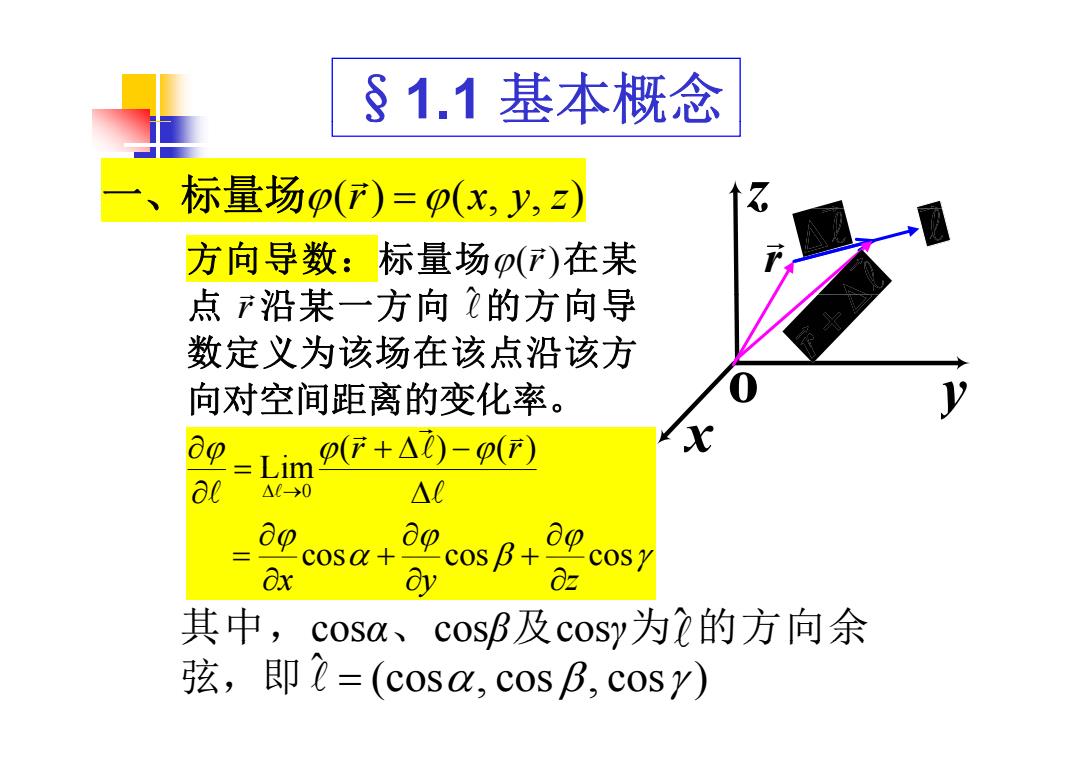
§1.1基本概念 标量场p()=p(x,y,z) 方向导数:标量场0()在某 点沿某一方向的方向导 数定义为该场在该点沿该方 向对空间距离的变化率。 ∂0 Lim p(行+△C)-p(F) al △0→0 △U 0 cosa 8x op cosB+ 8y osy 8z 其中, c0S0、 cosB及cosy为)的方向余 弦,即C=(cosa,cosB,cosY)
§1.1 基本概念 一 、标量场(r) (x, y, z) 、标量场(r) (x, y, z) z 方向导数:标量场 (r) 在某 点 沿某 方向 ˆ 的方向导 z r 点 r沿某一方向 的方向导 数定义为该场在该点沿该方 o ( ) ( ) Lim r r 向对空间距离的变化率。 o x y cos cos cos Lim 0 cos cos cos x y z 其中,cosα、cosβ及cosγ为ˆ 的方向余 弦,即 (cos , cos , cos ) ˆ

§1.1基本概念 梯度:标量场在某点的梯度为一矢量。 其大小等于该点所有方向导数的最大 值,其方向为取得该最大值的方向。 -gadp.t-与i的夹角 其中,grado即为梯度: grado ∂x gradient Nabla或Hamilton算子,读作“del
§1.1 基本概念 标量场在某点的梯度为一矢量 §1.1 基本概念 梯 度:标量场在某点的梯度为 矢量。 其大小等于该点所有方向导数的最大 梯 度: 值,其方向为取得该最大值的方向。 ) d ˆ d ( d ˆ 与的夹角 grad grad cos(grad 与的夹角) 其中 d 即为梯度 d ˆ ˆ ˆ 其中,grad 即为梯度: z z y y x x grad ˆ ˆ ˆ gradient Nabla或Hamilton算子, 读作“del
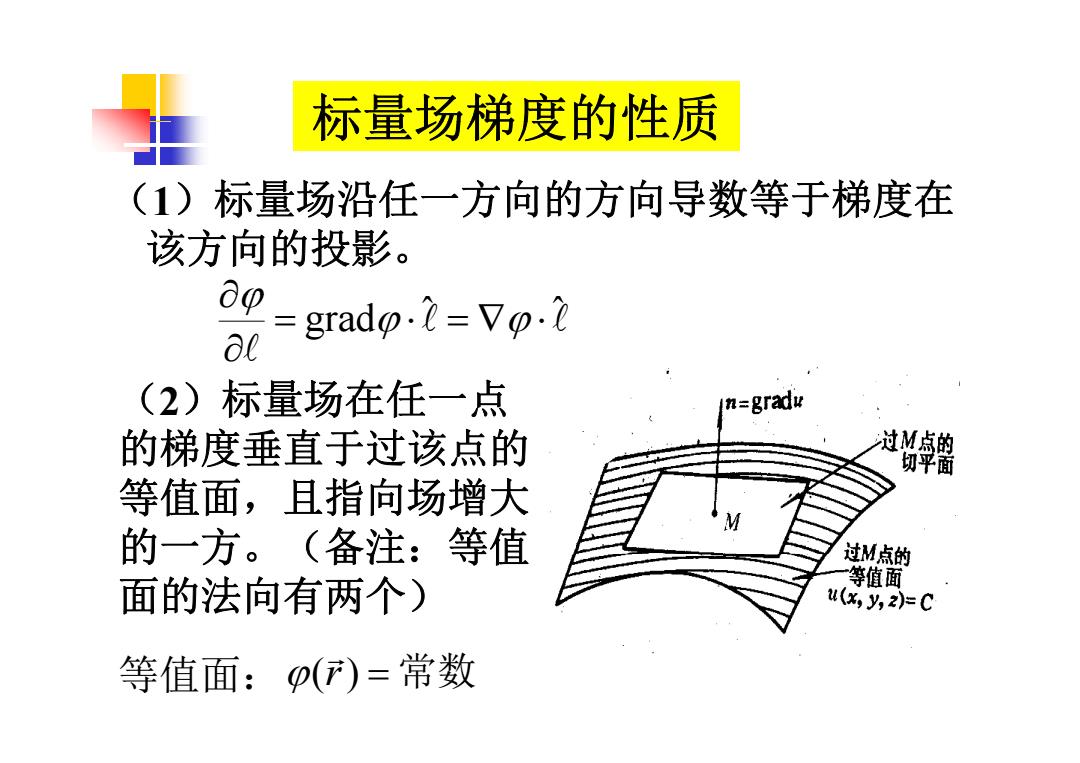
标量场梯度的性质 (1)标量场沿任一方向的方向导数等于梯度在 该方向的投影。 0g-grado.l-Vo. (2)标量场在任一点 n=gradu 的梯度垂直于过该点的 过M点的 切平面 等值面,且指向场增大 的一方。(备注:等值 过M点的 面的法向有两个) 等值面 (,y,2=C 等值面:p()=常数
标量场梯度的性质 ( 1 )标量场沿任 方向的方向导数等于梯度在 一方向的方向导数等于梯度在 该方向的投影。 grad ˆ ˆ ( 2 )标量场在任 点 标量场在任 一 点 的梯度垂直于过该点的 等值面,且指向场增大 的 方一 方。(备注 :等值 面的法向有两个) 等值面: ( r ) 常数

标量场梯度的性质 (3)一个标量场的梯度确定,则该标量场 也随之确定,最多相差一个任意常数。 对场的描述 标量场 其梯度场 对一个标量场,可直接研究该标量场, 亦可研究其梯度场: 对一个矢量场,若其可表为一个标量场 的梯度,则通常研究此标量场较为方便
标量场梯度的性质 ( 3 ) 一个标量场的梯度确定 ,则该标量场 也随之确定,最多相差一个任意常数。 对场的描述 标量场 其梯度 场 对一个标量场,可直接研究该标量场, 亦可研究其梯度场 ; 对一个矢量场,若其可表为一个标量场 的梯度 ,则通常研究此标量场较为方便
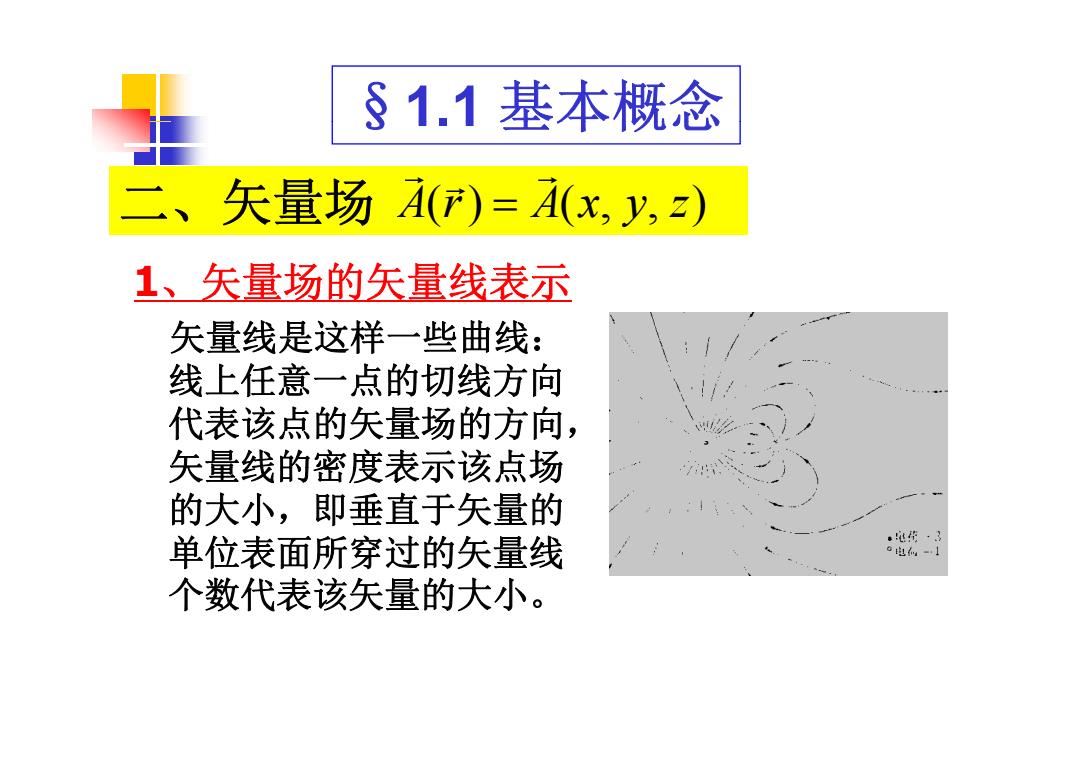
§1.1基本概念 二、矢量场A(T)=A(x,y,z) 1、矢量场的矢量线表示 矢量线是这样一些曲线: 线上任意一点的切线方向 代表该点的矢量场的方向, 矢量线的密度表示该点场 的大小,即垂直于矢量的 克·3 单位表面所穿过的矢量线 0电-1 个数代表该矢量的大小
§1.1 基本概念 二 矢量场 基本概念 A(r) A(x y z) 二、矢量场 1、矢量场的矢量线表示 A(r) A(x, y, z) 1、矢量场的矢量线表示 矢量线是这样一些曲线: 线上任意 点的切线方向 一点的切线方向 代表该点的矢量场的方向, 矢量线的密度表示该点场 的大小,即垂直于矢量的 单位表面所穿过的矢量线 个数代表该矢量的大小
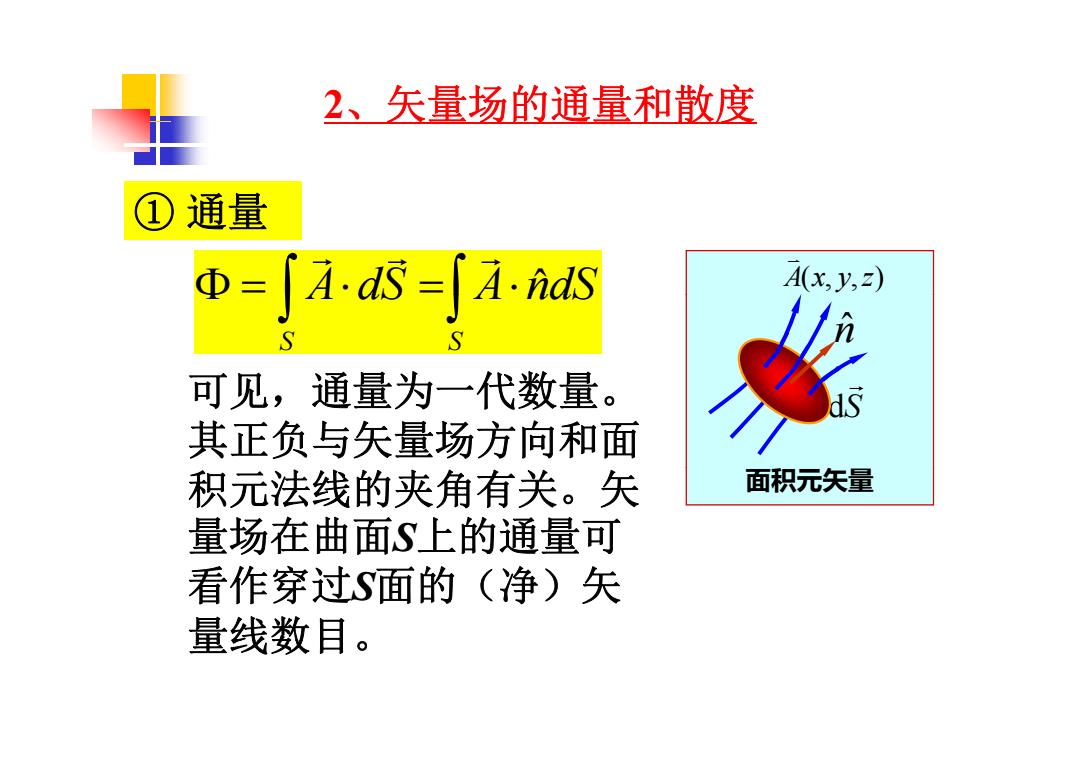
2、矢量场的通量和散度 ①通量 Φ=JiS=∫aiaS A(x,y,) 可见,通量为一代数量。 其正负与矢量场方向和面 积元法线的夹角有关。矢 面积元矢量 量场在曲面S上的通量可 看作穿过S面的(净)矢 量线数目
2、矢 场的 和散度 量场的通量和散度 ① 通量 A(, ,) xyz A dS A nˆdS 可见 通量为 代数量 n ˆ S S A dS A ndS 可见,通量为一代数量。 其正负与矢量场方向和面 S d 积元法线的夹角有关。矢 矢 量场在曲面S上的通量可 面积元矢量 场 面 看作穿过S面的(净)矢 量线数目
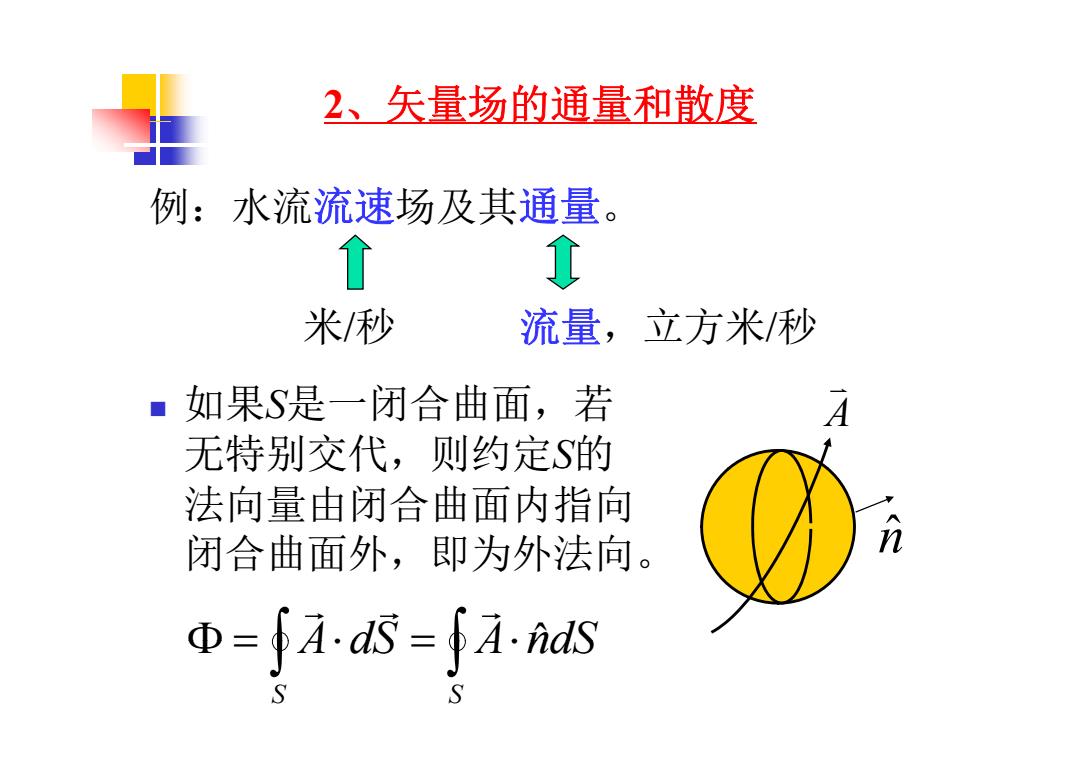
2、矢量场的通量和散度 例:水流流速场及其通量。 ↑ 米/秒 流量,立方米/秒 如果S是一闭合曲面,若 A 无特别交代,则约定S的 法向量由闭合曲面内指向 闭合曲面外,即为外法向。 Φ=fA.as=A.nds S
2、矢 场的 和散度 量场的通量和散度 例:水流流速场及其通量。 米/秒 流量,立方米/秒 如果S是一闭合曲面,若 无特别交代,则约定S的 A 无特别交代,则约定S的 法向量由闭合曲面内指向 闭合曲面外,即为外法向。 n ˆ A dS A nˆdS S S A dS A ndS