
第三章静电场边 值问题的求解方法 场的分析方法回顾:直接积分法: 高斯定理(+迭加原理)。 本章:在给定边界条件下求解泊松方程。 本章目录: §3.1唯一性定理 §3.2镜像法 §3.3解析函数法 §3.4分离变量法 §3.5格林函数法
第三章 静电场边 值问题的求解方法 §3.1 唯一性定理 §3.2 镜像法 §3.3 解析函数法 §3.4 分离变量法 §3.5 格林函数法 本章目录: 场的分析方法回顾:直接积分法; 高斯定理(+迭加原理)。 本章:在给定边界条件下求解泊松方程
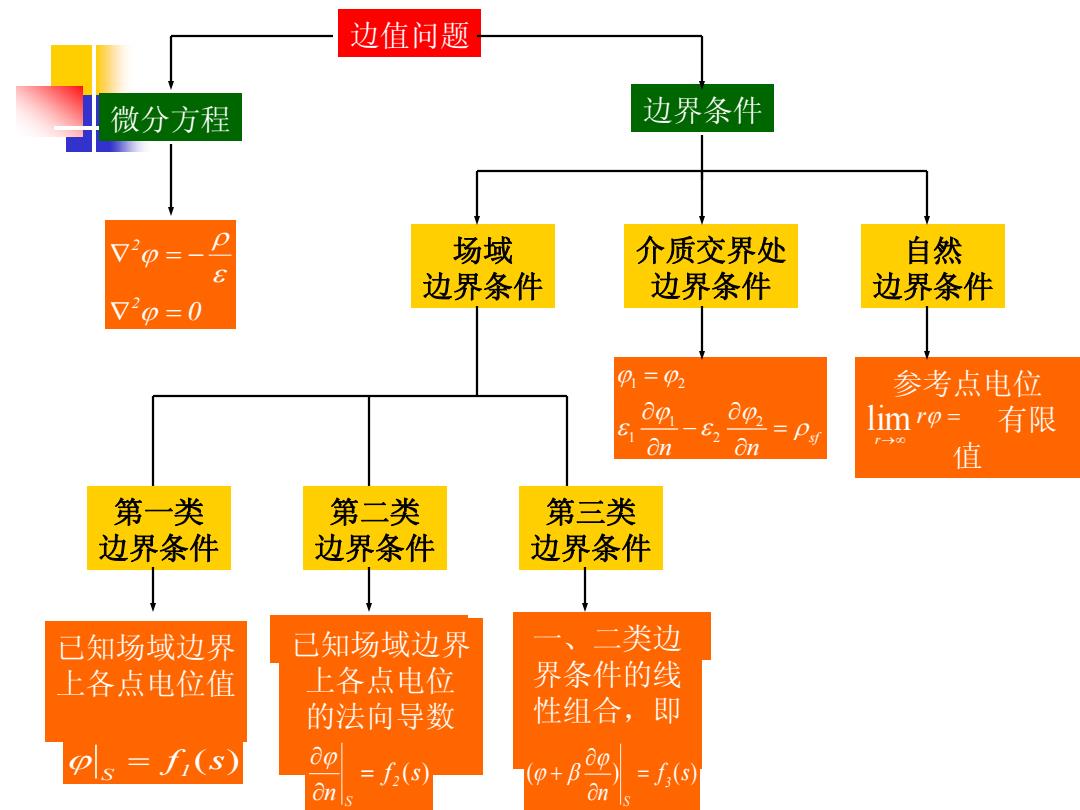
边值问题 微分方程 边界条件 场域 介质交界处 自然 边界条件 边界条件 边界条件 V2o=0 01=p2 参考点电位 00-n 02二P到 limro= 有限 On 值 第一类 第二类 第三类 边界条件 边界条件 边界条件 已知场域边界 已知场域边界 、二 类边 上各点电位值 上各点电位 界条件的线 的法向导数 性组合,即 Ps=f(s) 00 =3(s) =f(s)
自然 边界条件 参考点电位 有限 值 r r lim 边值问题 微分方程 边界条件 场域 边界条件 介质交界处 边界条件 第一类 边界条件 第二类 边界条件 第三类 边界条件 已知场域边界 上各点电位 的法向导数 一、二类边 界条件的线 性组合,即 0 2 2 1 2 1 2 1 2 sf n n f (s) n 2 S ( ) f (s) n 3 S 已知场域边界 上各点电位值 f (s) S 1
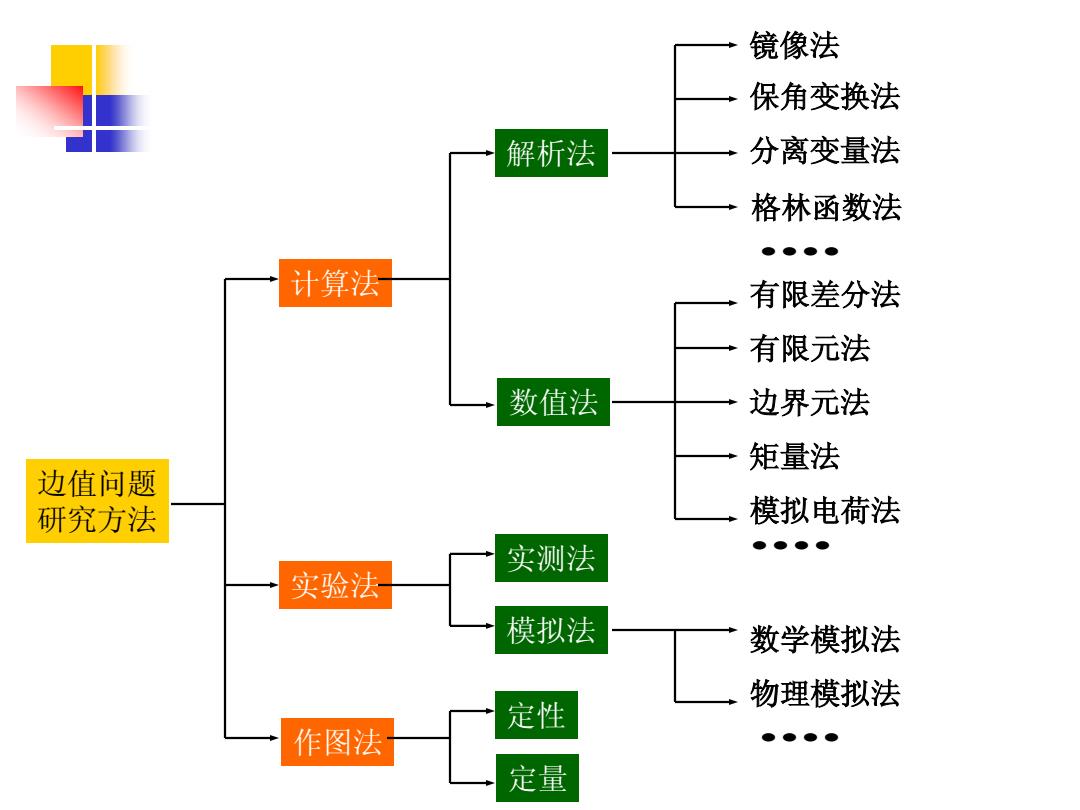
镜像法 保角变换法 解析法 分离变量法 格林函数法 ●●●● 计算法 有限差分法 有限元法 数值法 边界元法 矩量法 边值问题 研究方法 模拟电荷法 实测法 实验法 模拟法 数学模拟法 物理模拟法 定性 作图法 ●●●● 定量
边值问题 研究方法 计算法 实验法 作图法 解析法 数值法 实测法 模拟法 定性 定量 镜像法 分离变量法 格林函数法 保角变换法 有限差分法 有限元法 边界元法 矩量法 模拟电荷法 数学模拟法 物理模拟法

§3.1唯一性定理 设自由电荷分布在有限区域,介质线性各向同性分 区均匀。若 ①给定求解域内的自由电荷体密度和介质交界处 的自由电荷面密度以及介质的介电常数; 2 给定求解区域边界上电位的值或其法向导数值 (无限远处:0~r1) 在介质交界处满足: 0j Pi=Pi, 01一8j 8i on 二Dsf 介质i 介质j 则泊松方程的解唯一,最多相差一任意常数。如在 (部分)边界上给定电位值,则解唯一
§3.1 唯一性定理 设自由电荷分布在有限区域,介质线性各向同性分 区均匀。若 ① 给定求解域内的自由电荷体密度和介质交界处 的自由电荷面密度以及介质的介电常数; ② 给定求解区域边界上电位的值或其法向导数值 (无限远处: ~r -1) ③ 在介质交界处满足: i j, sf j j i i n n 则泊松方程的解唯一,最多相差一任意常数。如在 (部分)边界上给定电位值,则解唯一。 介质 i 介质 j nˆ i j

§3.1唯一性定理 【证】: V2p:=-pn/8: 设有二组不同的解:p,p2 令p,=p0-p,2, 则φ满足齐次方程和齐次边界条件。 标量格林第一定理: v+(wo(wyaw=j.p0as 令p=p,Ψ=01 zReg+6awgir-2ce8g5 川 0 0
【证】: i fi i / 2 设有二组不同的解: (1) i , (2) i 令 (1) (2) i i i , 则 i 满足齐次方程和齐次边界条件。 标量格林第一定理: V S dS n dV [ ( ) ( )] 2 令 , i S i i i i i V i i i i i i dS n dV i [( ( ) ( )] 2 §3.1 唯一性定理 0 0

§31唯一性定理 8,>0→vp=0→g=CC 电位连续,C与无关。 p,=p2)+C 若在边界某处给定电位值,则C=0 意义: ■指出了解唯一的条件; ■给求解方法提供了自由度(只需找到一个解 满足方程及边界条件即可)
i i i Ci C 0 0 2 意义: 指出了解唯一的条件; 给求解方法提供了自由度(只需找到一个解 满足方程及边界条件即可)。 电位连续,C与i无关。 i i C (1) (2) 若在边界某处给定电位值,则 C=0 §3.1 唯一性定理
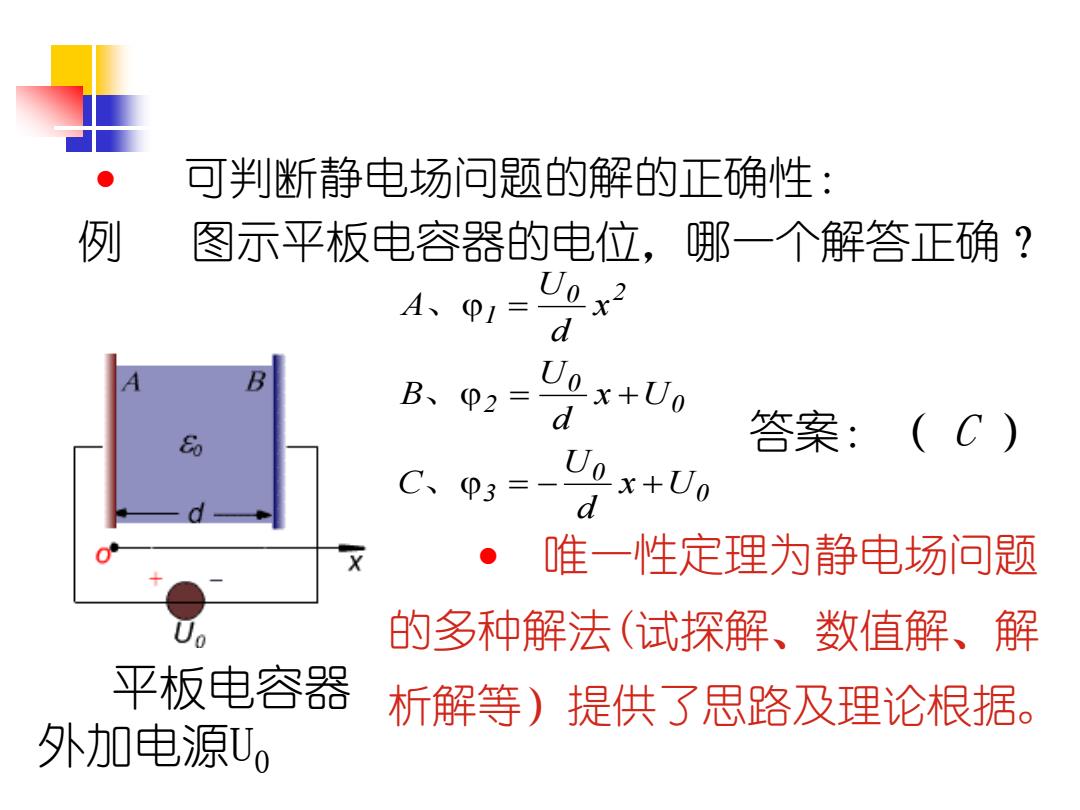
可判断静电场问题的解的正确性: 例 图示平板电容器的电位,哪一个解答正确? A、01= d B、02= x+Uo d 答案:(C) C、03=- Uox+Uo d 唯一性定理为静电场问题 的多种解法(试探解、数值解、解 平板电容器 析解等)提供了思路及理论根据。 外加电源Uo
可判断静电场问题的解的正确性: 例 图示平板电容器的电位,哪一个解答正确? 0 0 3 0 0 2 0 2 1 x U d U C x U d U B x d U A 、 、 、 答案:( C ) 唯一性定理为静电场问题 的多种解法(试探解、数值解、解 平板电容器 析解等)提供了思路及理论根据。 外加电源U0

§3.2镜像法 一j 种尝试方法。 数学基础:唯一性定理。 物理基础: 等效思想。利用反问题或逆问题 答案的不唯一性。 因果关系: 例:等效电阻。 求解区域外包括边界上的电荷分布对求解区 域内场的贡献: 例:点电荷,球对称分布电荷
§3.2 镜像法 一种尝试方法。 数学基础: 唯一性定理。 物理基础: 等效思想。利用反问题或逆问题 答案的不唯一性。 因果关系: 例:等效电阻。 求解区域外包括边界上的电荷分布对求解区 域内场的贡献: 例:点电荷,球对称分布电荷

§3.2镜像法 求解区域外包括边界上的电荷分布对求解区域 内场的贡献可用场在求解区域边界上行为来代 替或规定: 例:泊松方程的形式解 {6aC-品}aw 例:边界条件,给定电位值或其法向导数值, 对方程的通解进行选择。“滤波器”!
§3.2 镜像法 求解区域外包括边界上的电荷分布对求解区域 内场的贡献可用场在求解区域边界上行为来代 替或规定: 例:泊松方程的形式解 S V dS n R r n r R dV R r r 1 ( ) 1 ( ) 4 1 ( ) 4 1 ( ) 0 例:边界条件,给定电位值或其法向导数值, 对方程的通解进行选择。“滤波器”!

§3.2镜像法 镜像法: ☑对求解区域内具有相同贡献或其产生的场与求 解区域内电荷分布产生的场迭加能满足边界条件 的求解区域外及边界上的电荷分布是不唯一的, 有无数种可能的分布。 ☑镜像法尝试从上述分布中寻找一种简单、便于 计算的分布,替代原始问题中的实际分布。 ☑上述做法是否可行?通过能否满足边界条件进 行检验!
§3.2 镜像法 镜像法: 对求解区域内具有相同贡献或其产生的场与求 解区域内电荷分布产生的场迭加能满足边界条件 的求解区域外及边界上的电荷分布是不唯一的, 有无数种可能的分布。 镜像法尝试从上述分布中寻找一种简单、便于 计算的分布,替代原始问题中的实际分布。 上述做法是否可行?通过能否满足边界条件进 行检验!