
第六章时变电磁场 本章目录: ×E=- aB §6.1麦克斯韦方程 8t §6.2电磁场的位函数表示 V×i=j,+ aD §6.3达朗贝尔方程的解 §6.4波印亭定理 V.B=0 §6.5唯一性定理 V.D=p §6.6准静态场与准静态近似 §6.6广义麦克斯韦方程组及对偶原理
第六章 时变电磁场 本章目录: B E §6.1 麦克斯韦方程 § 6 2 电磁场的位函数表示 E t D § 6 . 2 电磁场的位函数表示 §6.3 达朗贝尔方程的解 f D H J t §6.4 波印亭定理 § 6 5 唯 性定理 B 0 D § 6 . 5 唯 一性定理 §6.6 准静态场与准静态近似 D §6.6 广义麦克斯韦方程组及对偶原理
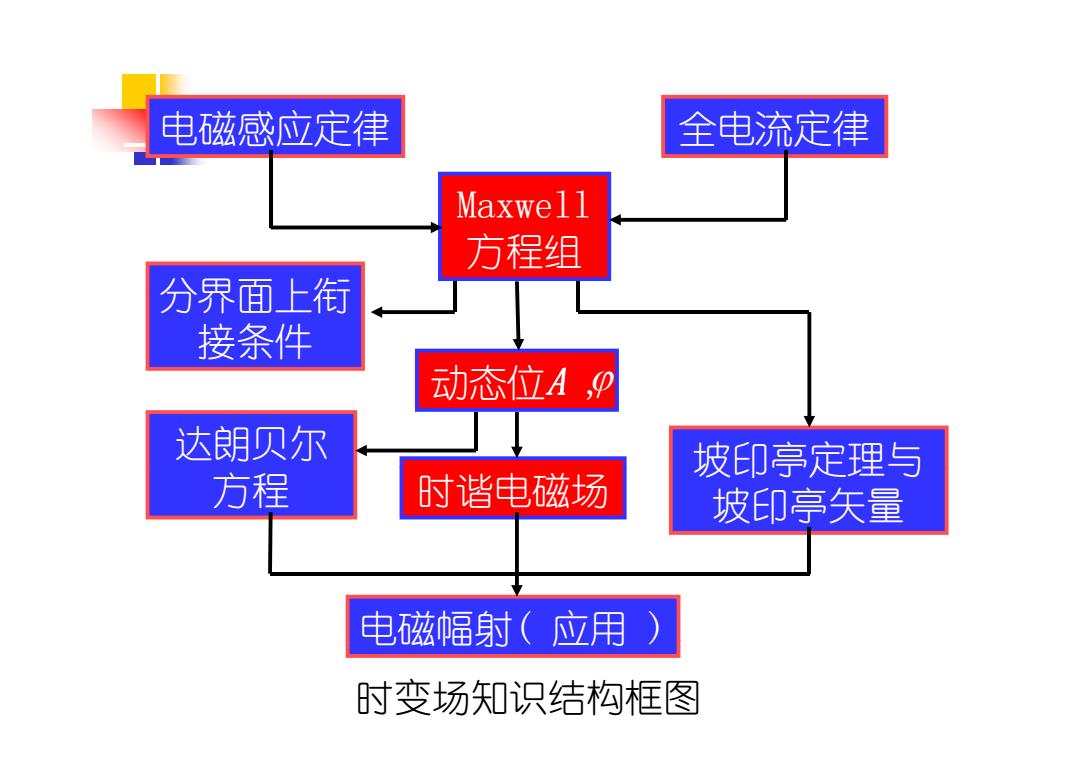
电磁感应定律 全电流定律 Maxwell 方程组 分界面上衔 接条件 动态位A,0 达朗贝尔 坡印亭定理与 方程 时谐电磁场 坡印亭矢量 电磁幅射(应用) 时变场知识结构框图
电磁感应定律 全电流定律 Maxwell 方程组 分界面上衔 接条件 动态位A , 达朗贝尔 坡印亭定理与 方程 时谐电磁场 坡印亭矢量 电磁幅射( 应用 ) 时变场知识结构框图 应用 )

§6.1麦克斯韦方程 麦克斯韦方程与边界条件 英国科学家麦克斯韦将静态场、恒定场、时变场的电磁基 本特性用统一的电磁场基本方程组高度概括。电磁场基本 方程组是研究宏观电磁场现象的理论基础。他在1864年英 国皇家学会宣读的论文“电磁场的动力学理论”中,提出 了电磁场的普遍方程,即现在的麦克斯韦方程,其主要贡献在于总结了静电学 和静磁学的物理规律以及电磁感应定律,借用矢量分析这一数学工具表达为简 洁的数学方程,即电磁场的散度、旋度方程,引入了位移电流的概念,消除了 方程中的矛盾,提出了这些方程普遍成立的假设,进一步预言了电磁波的存在, 1868年,麦克斯韦在他的论文“关于光的电磁波理论”中,提出光也是一种电 磁波,只不过频率较高而已,一切频率的电磁波都可以产生。1888年德国物理 学家赫兹用实验验证了电磁波的存在
§6.1 麦克斯韦方程 一、麦克斯韦 与边 条件 麦克斯韦方程与边界条件 英国科学家麦克斯韦将静态场、恒定场、时变场的电磁基 本特性用统一的电磁场基本方程组高度概括。电磁场基本 方程组是研究宏观电磁场现象的理论基础。他在1864年英 国皇家学会宣读的论文“电磁场的动力学理论”中,提出 了电磁场的普遍方程,即现在的麦克斯韦方程,其主要贡献在于总结了静电学 和静磁学的物理规律以及电磁感应定律,借用矢量分析这一数学工具表达为简 洁的数学方程,即电磁场的散度、旋度方程,引入了位移电流的概念,消除了 方程中的矛盾,提出了这些方程普遍成立的假设,进一步预言了电磁波的存在, 1868年,麦克斯韦在他的论文“关于光的电磁波理论”中,提出光也是一种电 磁波,只不过频率较高而已,一切频率的电磁波都可以产生。 1888年德国物理 学家赫兹用实验验证了电磁波的存在

§6.1麦克斯韦方程 7xE= )环路定理 静电场: B V.D= 高斯定理 8t 当由静电场变为时变场时,由电磁 感应定律 VxE=- aB 8t 高斯定律中电位移矢量己经包含了极化电荷的效 应,所以它依然适用于时变场,唯一不同的是电 位移矢量和自由电荷密度均为时变场量而已。 →V.D=p财 变化的磁场会产生电场
§6.1 麦克斯韦方程 0 : E 环路定理 静电场: D f 静电场 高斯定理 当由静电场变为时变场时,由电磁 感应定律 B E t 高斯定律中电位移矢量已经包含了极化电荷的效 应,所以它依然适用于时变场 所以它依然适用于时变场,唯 不同的是电 一 位移矢量和自由电荷密度均为时变场量而已。 D f 变化的磁场会产生电场

§6.1麦克斯韦方程 静磁场: V×i=jj 安培定理 V.B=0 高斯定理 对安培定律两边取散度→V.(V×H)=V·J,=0 由电荷守恒定律7j=- op 8t 显然当为时变场时 P0,上面两式矛盾。 8
§6.1 麦克斯韦方程 : 0 H J f B 安培定理 静磁场 B 0 高斯定理 H J 0 对安培定律两边取散度 ( ) 0 H J f J 对安培定律两边取散度 ( ) 由电荷守恒定律 f J t 由电荷守恒定律 0 t 显然当为时变场时 ,上面两式矛盾
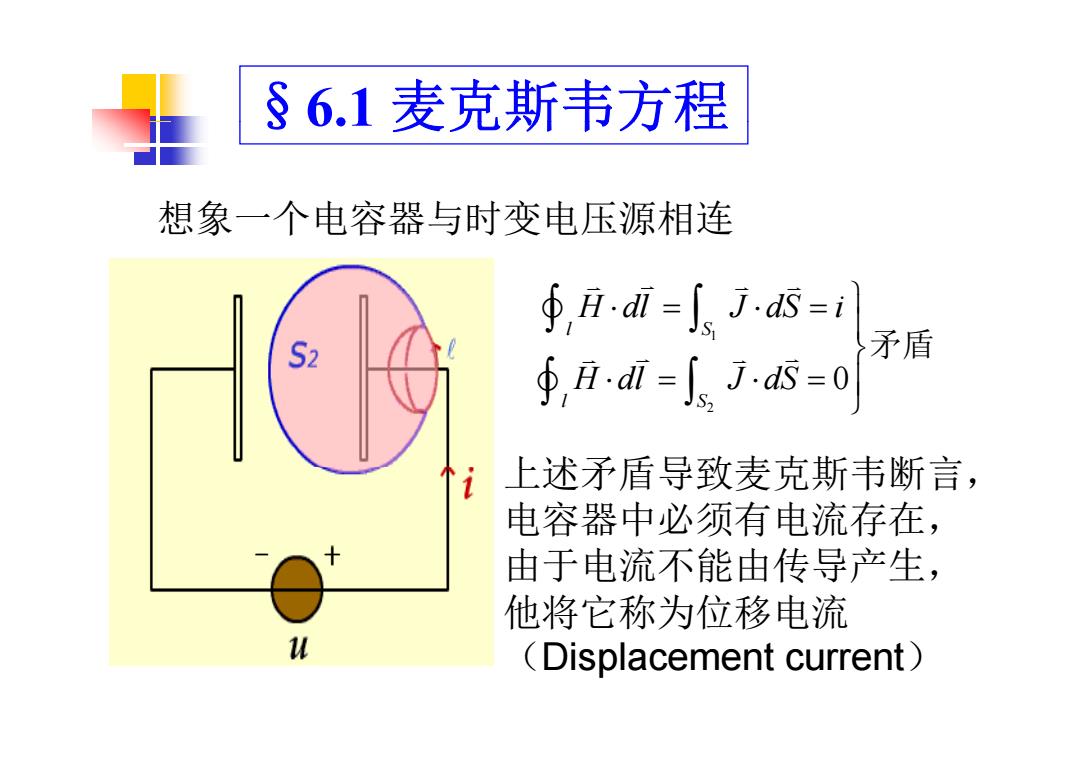
§6.1麦克斯韦方程 想象一个电容器与时变电压源相连 ∮,月i-Js=1 S2 矛盾 ∮,Aal=Jas=0 个i 上述矛盾导致麦克斯韦断言, 电容器中必须有电流存在, 由于电流不能由传导产生, 他将它称为位移电流 1认 (Displacement current)
§6.1 麦克斯韦方程 想象 个电容器与时变电压源相连 dl dS 想象一个电容器与时变电压源相连 1 0 l S H dl J dS i H dl J dS 矛盾 2 0 l S H dl J dS 上述矛盾导致麦克斯韦断言, 电容器中必须有电流存在, 由于电流不能由传导产生, 他将它称为位移电流 (Displacement current)

§6.1麦克斯韦方程 高斯定理V·D=Pj 电荷守恒定律VJ= →j,=- →Vxi=j,+ aD D 定义 为位移电流密度(A/m2) 由于位移电流的存在使得不仅变化的磁场产生电场, 变化的电场也可以产生磁场,即随时间变化的电场 和磁场可以作为对方的漩涡源,这样即使在没有电 荷电流的区域,电磁场也可以再产生和传播
§6.1 麦克斯韦方程 D f 高斯定理 f J t 电荷守恒定律 0 f f D D J J t t 2 / f t t D A D H J m f 定义: 为位移电流密度( ) t t 由于位移电流的存在使得不仅变化的磁场产生电场, 变化的电场也可以产生磁场,即随时间变化的电场 和磁场可以作为对方的漩涡源,这样即使在没有电 荷电流的区域,电磁场也可以再产生和传播
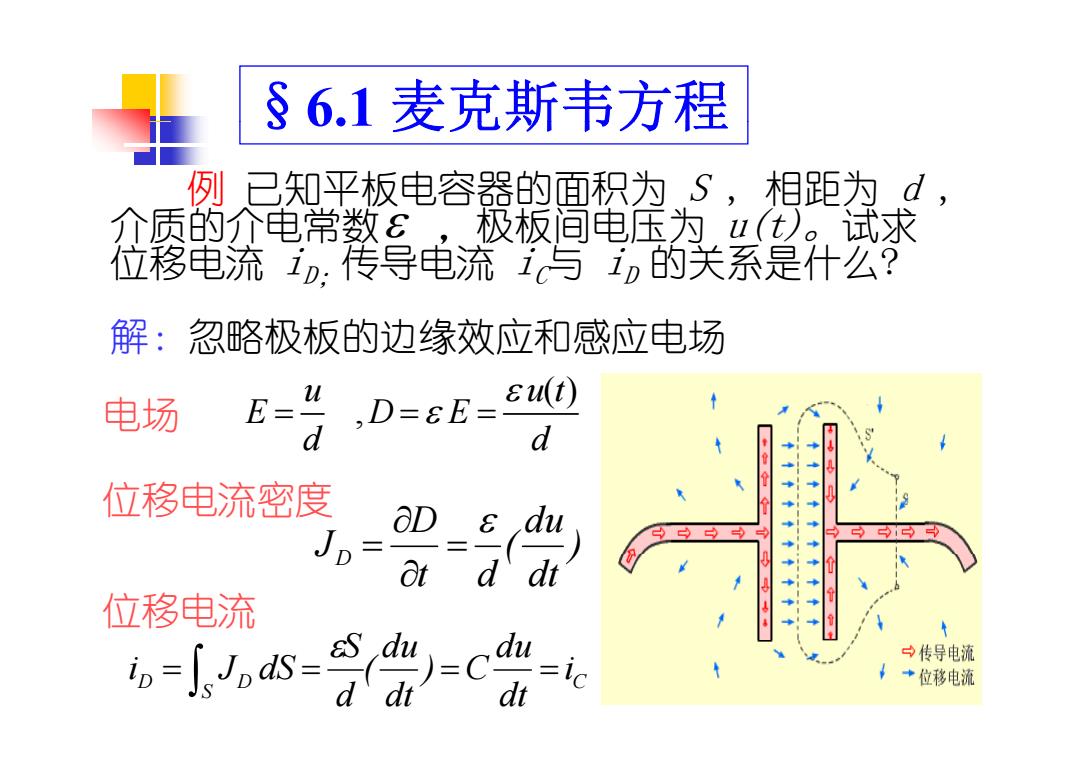
§6.1麦克斯韦方程 例已知平板电容器的面积为S,相距为d, 介质的介电常数8,极板间电压为,u(t)。试求 位移电流1o:传导电流1,与0的关系是什么? 解:忽略极板的边缘效应和感应电场 电场 E=1,D=EE= &(t) d d ! 位移电流密度 JD= Ot d 位移电流 1以s- 0=C du 中传导电流 dt →位移电流
§6.1 麦克斯韦方程 例 已知平板电容器的面积为 S , 相距为 d , 介质的介电常数 ,极板间电 为压 u( )t 。试求 位移电流 iD;传导电流 iC与 iD 的关系是什么? ( )t 解:忽略极板的边缘效应和感应电场 , u u t E DE d d 电场 位移电流密度 ) du ( D JD 位移电流 ) dt ( t d JD S d d C S D D i dt du ) C dt du ( d S i J dS

§6.1麦克斯韦方程 由于磁力线永远是闭合的,所以静磁场的高斯定理 依然成立,只是磁感应强度为时变的而己。 所以可以得到麦克斯韦方程组: 又xi=J,+ aD 全电流定律 7×E= aB 电磁感应定律 8t ☑.B=0 磁通连续性原理 V.D=P 高斯定律
§6.1 麦克斯韦方程 由 于 磁 力 线 永 远 是 闭 合 的 , 所 以 静 磁 场 的 高 斯 定 理 B 由 于 磁 力 线 永 远 是 闭 合 的 所 以 静 磁 场 的 高 斯 定 依然成立,只是磁感应强度 为时变的而已。 所 以 可 以 得 到 麦 克 斯 韦 方 程 组 D H J 全 电 流 定 律 所 以 可 以 得 到 麦 克 斯 韦 方 程 组: H J f t B 全 电 流 定 律 0 B E t B 电磁感应定律 B 0 磁 通 连 续 性 原 理 D 磁 通 连 续 性 原 理 高斯定律

§6.1麦克斯韦方程 (D2-D)=P 边界条件 n×(E2-E,)=0 n(B2-B)=0 n×(i2-H)=J >麦克斯韦第一、二方程是独立方程,后面两个 方程可以从中推得。 >静态场和恒定场是时变场的两种特殊形式
§6.1 麦克斯韦方程 nD D ˆ ( ) 2 1 2 1 ( ) ˆ ( )0 sf nD D nE E 边界条件 2 1 2 1 ( )0 ˆ ( )0 nE E nB B 边界条件 2 1 ˆ ( ) sf nH H J 麦克斯韦第一、二方程是独立方程,后面两个 方程可以从中推得。 静态场和恒定场是时变场的两种特殊形式