
第二章线性空间 线性空间理论是线性泛函分析的重要组成部 分。应用线性泛函分析的方法可以把对许多数 学问题的处理方法加以系统化,在更抽象的意 义上理解初看来毫无关系的数学概念之间的本 质联系
第二章 线性空间 线性空间理论是线性泛函分析的重要组成部 分。应用线性泛函分析的方法可以把对许多数 学问题的处理方法加以系统化,在更抽象的意 义上理解初看来毫无关系的数学概念之间的本 质联系

第二章线性空间 1 线性空间; 2 线性变换; 3、 线性变换的本征值与本征向量: 4、 内积空间; 5、 正交化法; 6、 自伴算子; 7、 等距变换; 8、 正规变换的本征值与本征向量; 9、 平方可积函数空间; 10、完备正交归一函数集; 11、多项式逼近 12、完备正交归一集的例子: 13、正交多项式
1、 线性空间; 2、 线性变换; 3、 线性变换的本征值与本征向量; 4、 内积空间; 5、 正交化法; 6、 自伴算子; 7、 等距变换; 8、 正规变换的本征值与本征向量; 9、 平方可积函数空间; 10、完备正交归一函数集; 11 、多项式逼近 12 、完备正交归一集的例子; 13、 正交多项式 第二章 线性空间

§2.1线性空间 §2线性空间 一、群 设G是一元素集,“”是某种定义在G上的运算,对任意 a∈G,b∈G有(ab)∈G这种运算称为封闭运算。 定义:群为由集合G和封闭运算“”所组成的系统,记为{G,} 它满足以下三个公理: (1) 运算满足结合律:(a·b)c=a(b·c) (2) 存在单位元素e,有e.a=a:e=a (3)对任意的a∈G存在逆元素al满足 a-a=a.a=e 注意:当群满足运算的交换率:a·b=b·☑ 则称为Abel群或交换群
§ 2.1 线性空间 § 2 线性空间 一、群 设G是一元素集,“.”是某种定义在G上的运算,对任意 a G b G , 有 (a b G ) 这种运算称为封闭运算。 定义:群为由集合G和封闭运算“.”所组成的系统,记为 G, 它满足以下三个公理: (1)运算满足结合律: ( ) ( ) a b c a b c = (2) 存在单位元素e,有 (3)对任意的 a G 存在逆元素 满足 1 1 a a a a e − − = = 注意:当群满足运算的交换率: a b b a = 则称为Abel群或交换群。 e a a e a = =1 a −
§2.1线性空间 §2线性空间 例: (1)整数的集合,以普通的加法做运算, 构成Abel群。 此时0是单位元素,n和一n互为逆元素。 (2)二维旋转矩阵 r(p) cosp sino -sing cosp (g∈-x,]) 相对矩阵乘法也是一个Abel群。r(O)是单位元。r(p)和r(-p) 互为逆元素。 例:以上是满足交换律的即Abel群,有没有不满足交换律的例子? 三维旋转的集合是一个不可对易的连续群 先绕z轴转动90度,再绕y轴转动90度 一样? 先绕y轴转动0度,再绕z轴转动90度
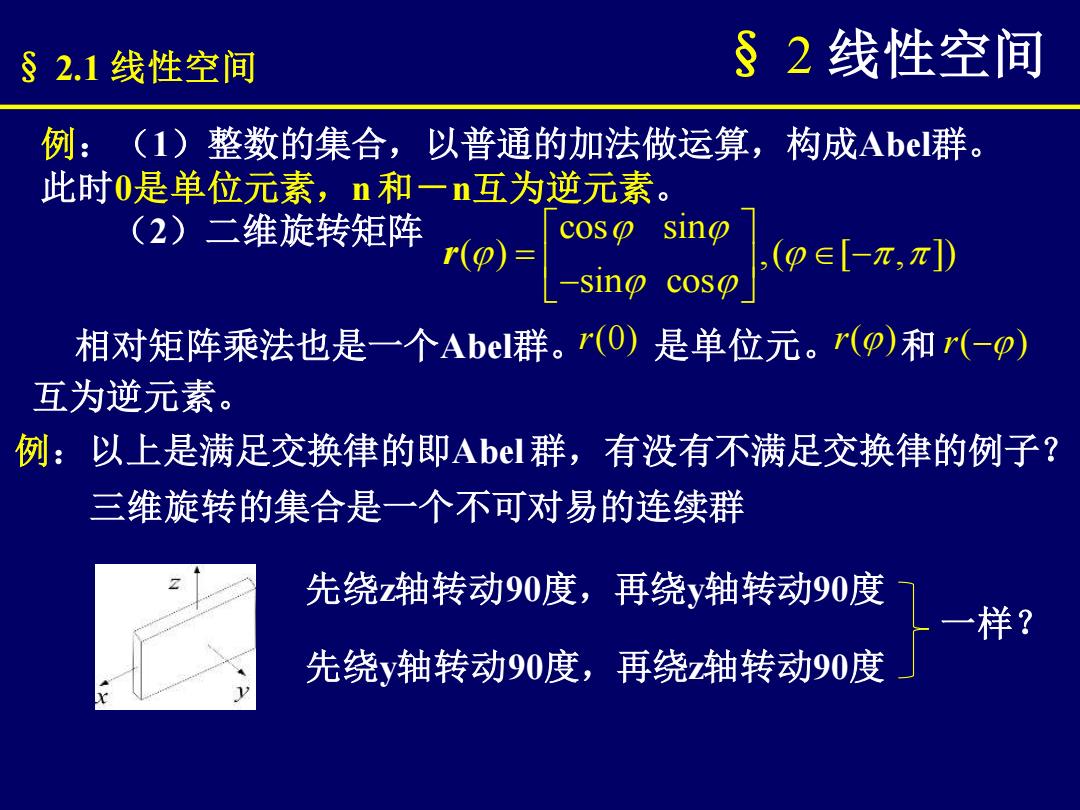
§ 2.1 线性空间 § 2 线性空间 例:(1)整数的集合,以普通的加法做运算,构成Abel群。 此时0是单位元素,n 和-n互为逆元素。 (2)二维旋转矩阵 cos sin ( ) ,( [ , ]) sin cos r = − − 相对矩阵乘法也是一个Abel群。 r(0) 是单位元。 r( ) 和 r( ) − 互为逆元素。 例:以上是满足交换律的即Abel 群,有没有不满足交换律的例子? 三维旋转的集合是一个不可对易的连续群 先绕z轴转动90度,再绕y轴转动90度 先绕y轴转动90度,再绕z轴转动90度 一样?

§2.1线性空间 §2线性空间 例:n个对象置换的集合。不满足交换律,不是Abel群。以n=3 为例。该集合包含3!=6个元素,可以表示为 12 23 12 -F 2 3 2 3 2 3 =B 定义一个乘法“*”,其法则是两个置换的乘积仍是一个置换 运算由右至左连续施行两次
§ 2.1 线性空间 § 2 线性空间 例:n个对象置换的集合。不满足交换律,不是Abel群。 以n=3 为例。该集合包含3!=6个元素,可以表示为 1 2 3 1 2 3 1 2 3 =I =F =D 1 2 3 3 1 2 2 3 1 1 2 3 1 2 3 1 2 3 =A =C =B 2 1 3 1 3 2 3 2 1 定义一个乘法“*”,其法则是两个置换的乘积仍是一个置换, 运算由右至左连续施行两次

§2.1线性空间 §2线性空间 二、域 域是满足以下三条公理的系统,记为 {F,+} (1)系统 {F,+}是一个具有单位元素0的Abel群; (2)设F'是除x=0以外的所有x∈F的集合, 则系统{F,}是一个具有单位元素e的Abel群; (3)相对于十,满足分配率,即 a.(b+c)=a.b+a.c
§ 2.1 线性空间 § 2 线性空间 二、域 域是满足以下三条公理的系统,记为 F, , + (1)系统 是一个具有单位元素0的Abel群; (2)设 是除 以外的所有 的集合, 则系统 是一个具有单位元素e的Abel群; (3)相对于+,满足分配率,即 F,+ F x = 0 x F F , a b c a b a c + = + ( )

§2.1线性空间 §2线性空间 例:所有有理数集合、实数集合、复数集合,相对于普通的 加法和乘法都构成了域。 有了域的概念我们可以定义线性空间 三、线性空间 (1)在非空集合V内的任一对元素间定义运算(十),使 {V,+}构成Abel群。(单位元素用0表示,x的逆元素用一x表示) 满足: x+(y+)=(x+y)+2 结合律 x+0=0+x=x 零元素 x+(-x)=(-x)+x=0 负元素 x+y=y+x 交换律
§ 2.1 线性空间 § 2 线性空间 例:所有有理数集合、实数集合、复数集合,相对于普通的 加法和乘法都构成了域。 有了域的概念我们可以定义线性空间 (1)在非空集合V内的任一对元素间定义运算(+),使 V,+ 构成Abel群。(单位元素用0表示,x的逆元素用-x表示) ( ) ( ) 0 0 ( ) ( ) 0 x y z x y z x x x x x x x x y y x + + = + + + = + = + − = − + = + = + 结合律 交换律 零元素 负元素 满足: 三、线性空间

§2.1线性空间 §2线性空间 (2)在数域F中的数与V中的元素之间定义一个纯量乘法运 算,对F中任意数C与V中任一元素x,都可由该运算唯一决 定V中的一个元素,记为y=Cx,数乘满足: 1x=x 数1的数乘 (cβ)x=c(Bx) 结合律 (a+B)x=ax+Bx 左分配律 a(x+y)=ax+ay 右分配律 则称V是数域F上的线性空间(向量空间),记为V)。 (以上8个公式为线性空间的8个公理)
§ 2.1 线性空间 § 2 线性空间 1 ( ) ( ) ( ) ( ) x x x x x x x x y x y = = + = + + = + 则称V是数域F上的线性空间(向量空间),记为V(F)。 (以上8个公式为线性空间的8个公理) (2)在数域F中的数与V中的元素之间定义一个纯量乘法运 算,对F中任意数 与V中任一元素 ,都可由该运算唯一决 定V中的一个元素y, 记为 y x = ,数乘满足: x 左分配律 右分配律 结合律 数1的数乘

§2.1线性空间 §2线性空间 例:n维向量空间的定义:是一个以n重有序数(552,…,5n) 为元素构成的集合,其中ξ∈F,定义向量加法 x+y=(5+7,52+72,…5n+7n) 其中:x=(51,52,…,5n),y=(7,72,…,7n) 向量数乘:Cx=(C51,C52,…,C5n) 零向量:0=(0,0,…,0)X的逆元:一x=(-51,一52,…,-5n) 可以证明,这个维向量空间是一个线性空间,记为R” 例:所有的复数的集合也是一个复线性空间
§ 2.1 线性空间 § 2 线性空间 例:n维向量空间的定义:是一个以n重有序数 为元素构成的集合,其中 ,定义向量加法 1 2 ( , , , ) n i F 1 1 2 2 ( , , ) n n x y + = + + + 1 2 ( , , , ) n 其中: x = 1 2 , ( , , , ) n y = 向量数乘: 1 2 ( , , , ) n x = 零向量: 0 (0,0, ,0) = x 的逆元: 1 2 ( , , , ) n − = − − − x 可以证明,这个n维向量空间是一个线性空间,记为 n R 例:所有的复数的集合也是一个复线性空间

§2.1线性空间 §2线性空间 例n次多项式的全体 Q[x]n={p=anx”+an-x”+.+ax +4|an,an1,a1,a∈R,且an≠0} 对于通常的多项式加法和乘数运算不构 成向量空间。 Q0p=0x”+0x-+…+0x+0E2[x]n ∴Q[x]n对多项式的加法与数乘运算不封闭
§ 2.1 线性空间 § 2 线性空间 1 1 1 0 1 1 0 1 [ ] ... | , ,..., , , 0} 0 0 0 ... 0 0 [ ] [ ] . n n n n n n n n n n n n n Q x p a x a x a x a a a a a R a p x x x Q x Q x − − − − = = + + + + = + + + + Q 次多项式的全体 且 对于通常的多项式加法和乘数运算不构 成向量空间。 对多项式的加法与数乘运算 例 不封闭