
第六章狭义相对论 1.证明牛顿定律在伽利略变换下是协变的,麦克斯韦方程在伽利略变换下不 是协变的。 解:伽利略变换为 x'=x-vt,y'=y 2'=z,t=t. 牛顿定律 F=ma 在ε系: F=m 在ε'系有 F=m'=m成, :牛顿定律在伽利略变换下是协变的。 由伽利略变换有 7=V'」 aaa ax' or=o ax or 在8系有: ×E=- OB aJ 81 VxBoo V.E=P 7.B=0 在ε'系有: OE' V'xE B Ox' @x'8t' V×B=4,J+40 0E'Ox' at' ax'ot' v.E=P,7.B=0 麦克斯韦方程在伽利略变换下不是协变的 2.设有两根互相平行的尺,在各自静止的参考系中的长度均为1。,它们以相 同速度ⅴ相对于某一参考系运动,但运动方向相反,且平行于尺子,求站在一根 尺子上测量另一根尺的长度。 解: 系 △x=I, ① △1=0, ②
第六章 狭义相对论 1.证明牛顿定律在伽利略变换下是协变的,麦克斯韦方程在伽利略变换下不 是协变的。 解:伽利略变换为 = = = − = ' , ' . ' , ' z z t t x x vt y y 牛顿定律 F = ma 在 系: F mx = . 在 系有 F mx mx = = , 牛顿定律在伽利略变换下是协变的。 由伽利略变换有 = . t x t t x + = 在 系有: = = = + = − E , B 0. , , 0 0 0 0 t J B J t B E 在 系有: = = + = + + = − , 0 , 0 0 0 0 E B t x x E t E B J t x x B t B E 麦克斯韦方程在伽利略变换下不是协变的 2.设有两根互相平行的尺,在各自静止的参考系中的长度均为 0 l ,它们以相 同速度 v 相对于某一参考系运动,但运动方向相反,且平行于尺子,求站在一根 尺子上测量另一根尺的长度。 解: ② ① 系 0, , = = t x l

系 Ar= ③ Mt' ④ ∑"系 △r"=4r'-v4r' ⑤ Vi-e 将③④代入⑤得 Ar"= 1+ c2 3.静止长度为1,的车厢,以速度v相对于地面S运行,车厢的后壁以速度v。 向前推出一个小球,求地面观察者看到小球从后壁到前壁的运动时间。 ∑系 解:A=6 ① '系 △r'+)△t' 1+ vuo △= =△t ② ,v2 1- ①代入②得
④ = ③ 系 2 2 2 2 0 1 , 1 c v l c v t c v l x − − = − ⑤ 系 2 2 1 c v x v x x − − = 将 ③ ④ 代入 ⑤ 得 0 2 2 2 2 1 1 l c v c v l x = − + = 2 2 2 2 0 1 1 c v c v l l + − = . 3.静止长度为 0 l 的车厢,以速度 v 相对于地面 S 运行,车厢的后壁以速度 0 v 向前推出一个小球,求地面观察者看到小球从后壁到前壁的运动时间。 解: 0 0 u l t = 系 ① 2 2 2 0 2 2 2 0 1 1 1 c v c v u t c v t u c v t t − + = − + = 系 ② ① 代入 ② 得

+ uo\1-c2 4.一辆以速度v运动的列车上的观察者,在经过某一高大建筑物时,看见其 避雷针上跳起一脉冲电火花,电光迅速传播,随后照亮了铁路沿线上的两铁塔。 求列车上观察者看到的两铁塔被电光照亮的时刻差,设建筑物及两铁塔都在一 直线上,与列车前进方向一致,铁塔到建筑物的地面距离已知都是。。 解: E系 △1=0 △x=2lo '系 A!'=_cAr 2lov V1-c cll-e 5.光源S与接收器R相对静止,距离为l。,S-R装置浸在均匀 无限的液体介质(静止折射率)中,诚对下列三种情况计算光源发出讯号到接 收器到讯号所经历时间, (1).液体介质相对于S-R装置静止。 (2).液体沿着S-R连线方向以速度v流动。 (3).液体垂直于S-R连线方向以速度v流动。 解:(1).由于介质的存在,所以光速为 所以 (以= c (2).由速度变换公式 4s巡+v 1+型 得:
2 2 0 2 0 0 1 1 c v u c u v l t − + = 4.一辆以速度 v 运动的列车上的观察者,在经过某一高大建筑物时,看见其 避雷针上跳起一脉冲电火花,电光迅速传播,随后照亮了铁路沿线上的两铁塔。 求列车上观察者看到的两铁塔被电光照亮的时刻差,设建筑物及两铁塔都在一 直线上,与列车前进方向一致,铁塔到建筑物的地面距离已知都是 0 l 。 解: 0 2 0 x l t = = 系 2 2 2 0 2 2 2 1 2 1 c v c l v c v x c v t − = − = 系 5.光源 S 与接收器 R 相对静止,距离为 0 l ,S-R 装置浸在均匀 无限的液体介质(静止折射率 n)中,诚对下列三种情况计算光源发出讯号到接 收器到讯号所经历时间, (1).液体介质相对于 S-R 装置静止。 (2).液体沿着 S-R 连线方向以速度 v 流动。 (3). 液体垂直于 S-R 连线方向以速度 v 流动。 解:(1).由于介质的存在,所以光速为 n c 所以 ( ) c nl t 0 1 = (2).由速度变换公式 2 1 c u v u v u x x x + + = 得:

us =n 1+y nc nc +V n (3)光的传播速度为 n 因为 u,=-y,4(=0, 因此 lx=1 将光线在S-R连线方向上的传播速度,变换到实验室参考系Σ上,有: h 1+ 由此得到∑系中光从S到R的时间: o △1= 6.在坐标系Σ中,有两个物体都以速度u沿x轴运动,在Σ系看来,它们一 直保持距离I不变,今有一观察者以速度ⅴ沿X轴运动,他看到这两个物体的距 离是多少? 解: ' ∑" 1' I" △f'=0 从∑到Σ”有:
nc v v n c ux + + = 1 ( ) v n c l nc v u l t x + + = = 0 0 2 1 (3).光的传播速度为 n c 因为 u v, y = − = 0, ut 因此 2 2 2 V n c ux = − 将光线在 S-R 连线方向上的传播速度 x u 变换到实验室参考系 上,有: 2 2 2 2 2 2 2 2 1 1 1 c v v n c c vu c v u u y x x − − = + − = , 由此得到 系中光从 S 到 R 的时间: 2 2 2 2 2 0 0 1 v n c c v l u l t x − − = = 。 6.在坐标系 中,有两个物体都以速度 u 沿 x 轴运动,在 系看来,它们一 直保持距离 l 不变,今有一观察者以速度 v 沿 x 轴运动,他看到这两个物体的距 离是多少? 解: l l l t = 0 从 到 有:
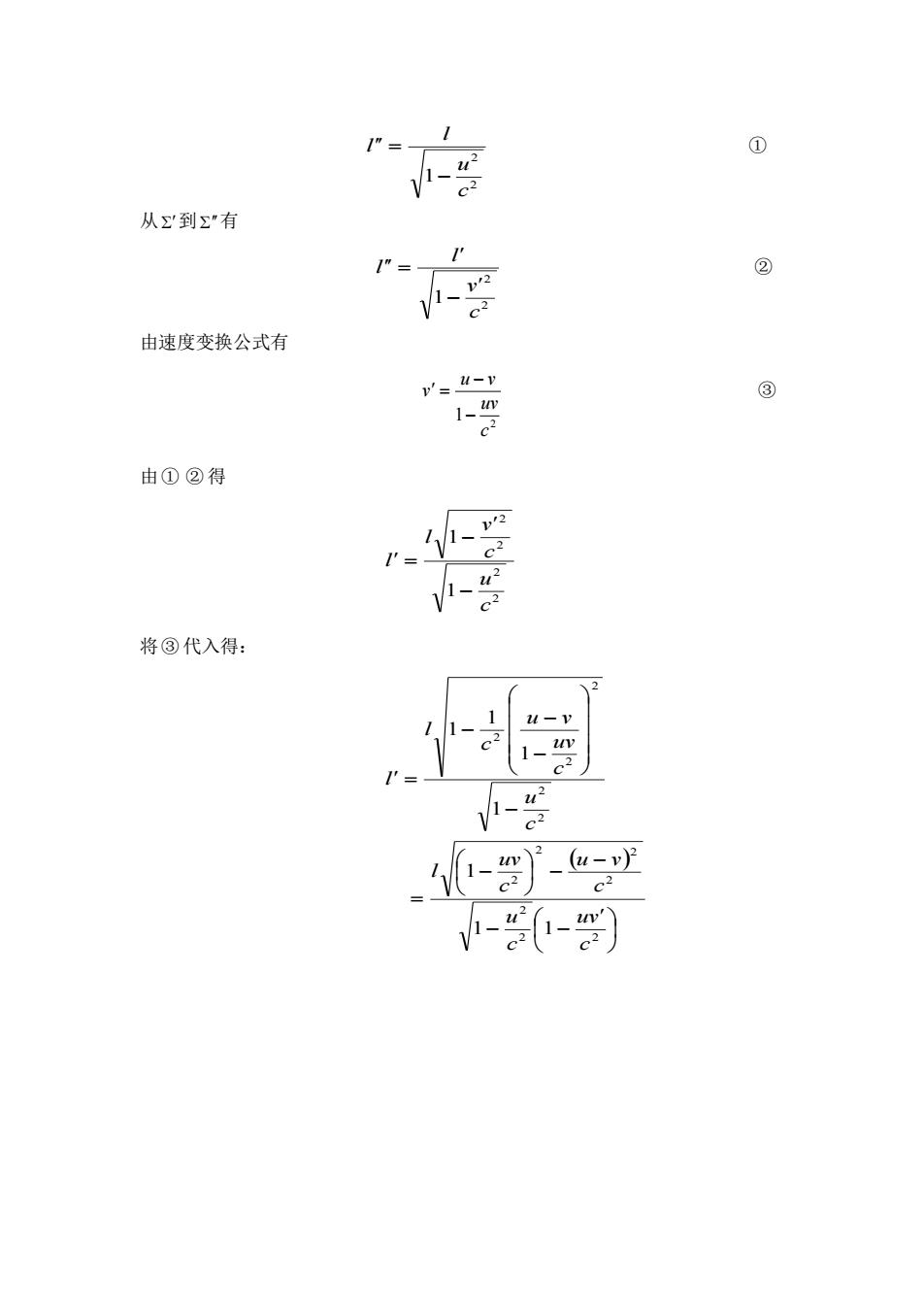
① 从'到Σ"有 - ② 由速度变换公式有 1-i ③ 由①②得 2 将③代入得: 2 u-V l、 u2 1- (u-v)2
2 2 1 c u l l − = ① 从 到 有 2 2 1 c v l l − = ② 由速度变换公式有 2 1 c uv u v v − − = ③ 由 ① ② 得 2 2 2 2 1 1 c u c v l l − − = 将 ③ 代入得: ( ) − − − − − = − − − − = 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 c uv c u c u v c uv l c u c uv u v c l l

2uv u2v2 u2 2uv v2 c2 -- (-- 7.一把直尺相对于Σ坐标系静止,直尺与x轴交角0。今有一观察者以速度 速度"沿x轴运动,他看到直尺与x轴交角0有何变化? 解: Σ系 '系 △y ① △y'=△y ④ △x ② △x= △r' ⑤ g0=4 ③ g'=4少 ⑥ x △r' g0=4y △y Ar' 1-a 8两个惯性系∑和Σ'中各放置若干时钟,统一惯性系中的诸时钟同步,∑ 相对于∑以速度V沿x轴方向运动,设两点系统圆点相遇时,t。=t。=0,问处 于∑系中某点(x,y,z)处的时钟与∑'系中何处的时钟相遇时,指示的时刻相同? 读数是多少? 解:两时钟相遇时
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 4 2 2 2 1 1 1 1 1 1 2 2 1 c u c uv c v c u l c u c u c v c uv c u c u v c uv l − − − − = − − − + − + − = 2 2 2 2 1 1 c u c v l − − = 7.一把直尺相对于 坐标系静止,直尺与 x 轴交角 。今有一观察者以速度 速度 v 沿 x 轴运动,他看到直尺与 x 轴交角 有何变化? 解: 系 系 y ① y = y ④ x ② 2 2 1 v v x x − = ⑤ x y tg = ③ x y tg = ⑥ 2 2 2 2 1 1 c v tg c v x y x y tg − = − = = 8.两个惯性系 和 中 各放置若干时钟,统一惯性系中的诸时钟同步, 相对于 以速度 v 沿 x 轴方向运动,设两点系统圆点相遇时, t 0 = t 0 = 0 ,问处 于 系中某点(x,y,z)处的时钟与 系中何处的时钟相遇时,指示的时刻相同? 读数是多少? 解:两时钟相遇时

x'=r(x-vt) y'=y Z=z ① 逆变换为 r-t ② ①②可得 t=t',x=-x 由②得: x=- 在∑系中看∑'中原点O'走过的距离: 4= 9.火箭由静止状态加速到v'=√0.9999c,设瞬时惯性系得加速度为同=20ms2, 问按照静止系的时钟和火箭内的时钟加速火箭各需要多少时间? 解:设∑'系是相对静止系以v'=√0.9999c运动的坐标系 dx' ..u= dt dy' a's dt' x=r(x'+vt) t=*总x k=+y c>
( ) = = = = − x c v t t - z z y y x x vt 2 ① 逆变换为 = + x c v t t 2 ② ①②可得 t = t,x = −x 由②得: = − − − 2 2 2 c v t 1 1 v c x 在 系中看 中原点 O 走过的距离: = + r 1 L0 x 1 t t L t 0 = = 9.火箭由静止状态加速到 v = 0.9999c,设瞬时惯性系得加速度为 2 v = 20m s , 问按照静止系的时钟和火箭内的时钟加速火箭各需要多少时间? 解:设 系是相对静止系以 v = 0.9999c 运动的坐标系 dt dx u x = dt dv a = x = (x + vt) = + x c v t t 2 2 x x x c u v 1 u v dt dx u + + = =

d w a= dus dt du'dt' dt'dt a 当飞船速度为v'=√0.9999c, u=0, ∴.a=a 又因为 dt=d a 所以 =tg0 N/ 8 1、v2 =47.5year 同理 t'=2.52year 10.一平面镜以速度v自左向右运动,一束频率为o。,与水平成0。夹角的平 面光波自右向左入射到镜面上,求反射光波的频率0及反射角O。垂直入射情况 如何? 解:坐标系建立如图:因为
dt c vu dt 1 2 x = + 3 2 3 x x x c vu 1 a dt dt dt du dt du a + = = = 当飞船速度为 v = 0.9999c, u x = 0, 3 a a = 又因为 a dv dt = 所以 47.5year c v 1 c v tg g c g dv t v 0 2 v 0 3 = − = = = 同理 t = 2.52year 10.一平面镜以速度 v 自左向右运动,一束频率为 0 ,与水平成 0 夹角的平 面光波自右向左入射到镜面上,求反射光波的频率 及反射角 。垂直入射情况 如何? 解:坐标系建立如图:因为

k.-(Rio] 且 ku =amkv 所以 k=:+总 ky=ky k,=k, @=0+k) 在Σ系中,入射波矢k,反射波矢K,,入射角日。, 由静止系中反射定律: 反射角日2=π-9,⊙2=01 ∴.cos02=cos0o 在两系中, kis=cose k2=cos0. _02cos02 k2x=- c 将其代入可得
= c i k k, 且 k k = a 所以 + x = x 2 c v k k k y = k y kz = kz = + vk x 在 系中,入射波矢 1 k ,反射波矢 2 k ,入射角 0 , 由静止系中反射定律: 反射角 2 0 = − , = 2 1 = 2 0 cos cos 在两系中, 1 1 1x cos c k = 2 2 2x cos c k = = 1 1 1x cos c k = 2 2 2x cos c k 将其代入 可得

cose -v cose c 1-Ycose, c cose,-v cose,= C 1- -cos0, ai=l1-csa) a=e1-cosa) 再联立 cose,= 1+ sin202=1- 2B-1+B2os8 1+B2-2Bcos0 1-B2 →sin0,=1+B2-2cos8, sine sin 0, g8,.=y[0B+cos日)+B0+kos8】 又 02=01 .02 1+B2-2os80, 1-B2 若v远小于c,则 B≈0 cos82≈-cos8 tg02≈tg0 02≈01
1 1 1 cos c v 1 c v cos cos − − = 2 2 2 cos c v 1 c v cos cos − − = , = − 1 1 1 cos c v 1 = − 2 2 2 cos c v 1 再联立 2 1 2 2 1 2 cos c v 2 c v 1 cos c v 1 c v 2 cos + − − + = ( ) 2 2 2 2 2 1 2 cos 2 1 cos sin 1 + − − + = − 1 1 2 2 2 sin 1 2 cos 1 sin + − − = ( ) ( ) 1 1 2 1 2 cos 1 cos sin tg + + + = 又 = 2 1 2 1 1 2 2 1 1 2 cos − + − = 若 v 远小于 c,则 0 2 1 cos −cos 2 1 tg tg 2 1