电子科技大学：《振动理论与声学原理 Vibration and Acoustics》课程教学资源（课件讲稿）第三章 单自由度系统受迫振动

上节课知识回顾 口单自由度无阻尼振动系统的特点是什么？ 口单自由度系统自由振动响应曲线具有什么 特征？ x(t)=Asin(@,t+p) 口求解系统固有频率的方法有哪些？

1 上节课知识回顾 p 单自由度无阻尼振动系统的特点是什么？ p 单自由度系统自由振动响应曲线具有什么 特征？ p 求解系统固有频率的方法有哪些？ ( ) sin( ) n x t  A  t 

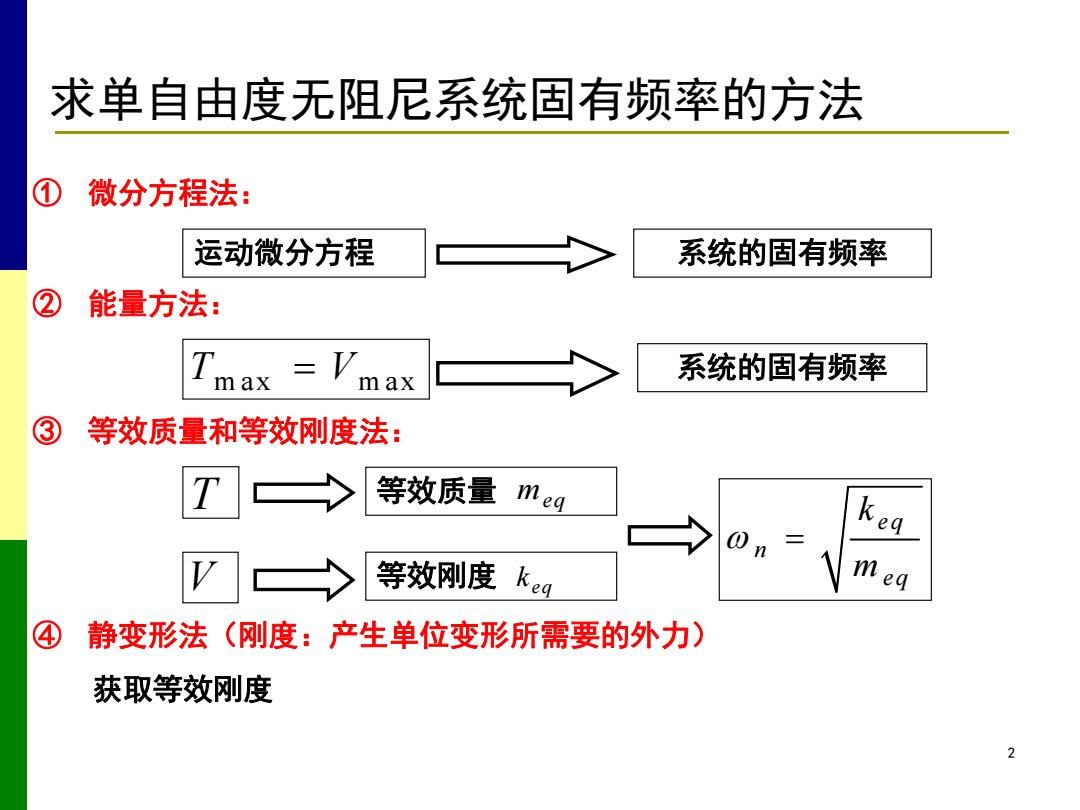
求单自由度无阻尼系统固有频率的方法 ① 微分方程法： 运动微分方程 系统的固有频率 能量方法： Tmax 系统的固有频率 max 等效质量和等效刚度法： 等效质量 meg n 等效刚度 keg m eq ④ 静变形法（刚度：产生单位变形所需要的外力） 获取等效刚度 2

2 ① 微分方程法： 运动微分方程 系统的固有频率 求单自由度无阻尼系统固有频率的方法 ② 能量方法： ③ 等效质量和等效刚度法： Tm ax  V m ax 系统的固有频率 T 等效质量 meq V 等效刚度 eq k eq n eq k m   ④ 静变形法（刚度：产生单位变形所需要的外力） 获取等效刚度

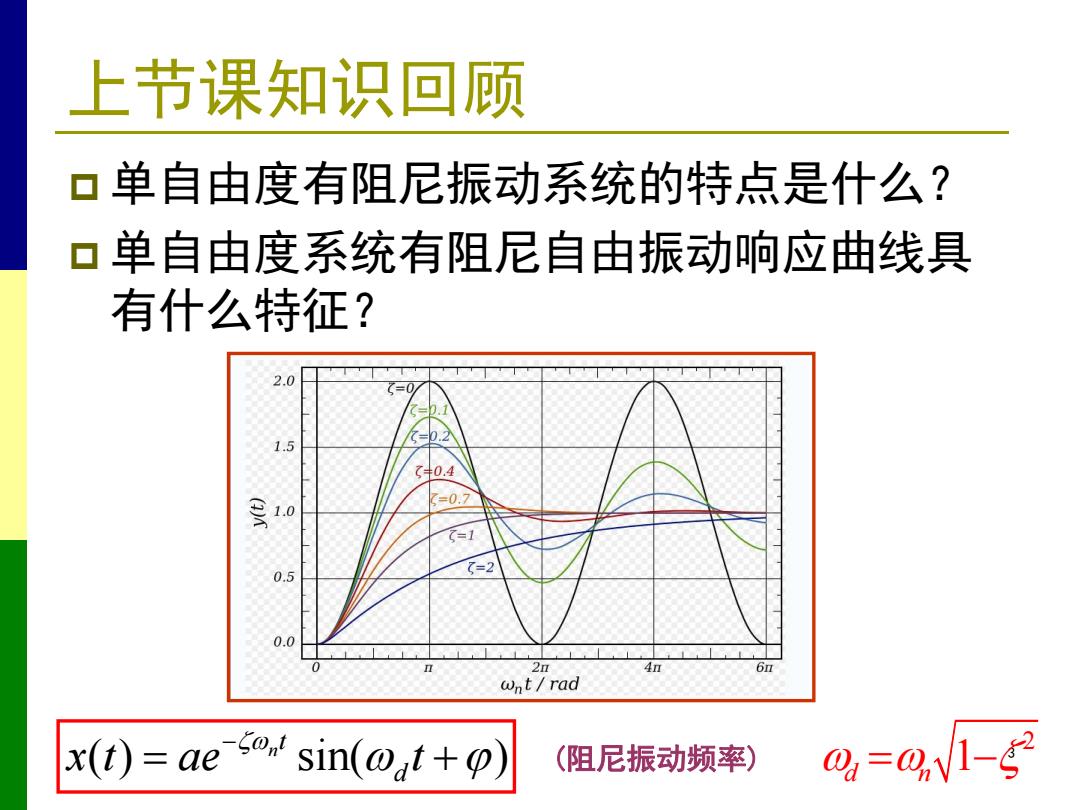
上节课知识回顾 口单自由度有阻尼振动系统的特点是什么？ 口单自由度系统有阻尼自由振动响应曲线具 有什么特征？ 2.0 .5 (0.4 10 =0.7 0.5 0.0 2 wnt rad x(t)=ae ssin(t) (阻尼振动频率) 0=0N1-g号

3 上节课知识回顾 p 单自由度有阻尼振动系统的特点是什么？ p 单自由度系统有阻尼自由振动响应曲线具 有什么特征？ ( ) sin( ) n t d x t ae t       2 1 d n (阻尼振动频率)  

第三章 单自由度系统受迫振动 ◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆中中中◆◆◆中◆中中中◆中◆中◆◆中◆0年◆中0带000000年◆◆年中◆中◆◆0◆◆年◆◆年◆09 库伦（1736一1806)法国物理学家、军事 工程师。1779年，总结其早年工作的《简 单机械理论》一书面世，该书揭示了摩擦 力和正压力之间的关系，即熟知的库伦摩 擦定律。1784年，他得到了刚体微幅扭振 问题的解。在国际单位制中，电荷的单位 :库伦就是以他的名字命名的

库伦（1736－1806）法

课堂讨论主题3： 口主题：研讨工程中存在的“振动隔离”和 “临界转速”问题 口时间：待定 口主题：在“振动隔离”和“临界转速”两个专 题中选择其一，各小组查阅国内外文献。 口课堂PPT交流与讨论，每组15分钟。 5

课堂讨论主题3： 5 p 主题：研讨工程中存在的“振动隔离”和 “临界转速”问题 p 时间：待定 p 主题：在“振动隔离”和“临界转速”两个专 题中选择其一，各小组查阅国内外文献。 p 课堂PPT交流与讨论，每组15分钟

教学内容 口线性系统的受迫振动 ·简谐力激励的强迫振动 ·稳态响应的特性 ·受迫振动的过渡阶段 ·简谐惯性力激励的受迫振动 ·工程中的受迫振动问题 6

6

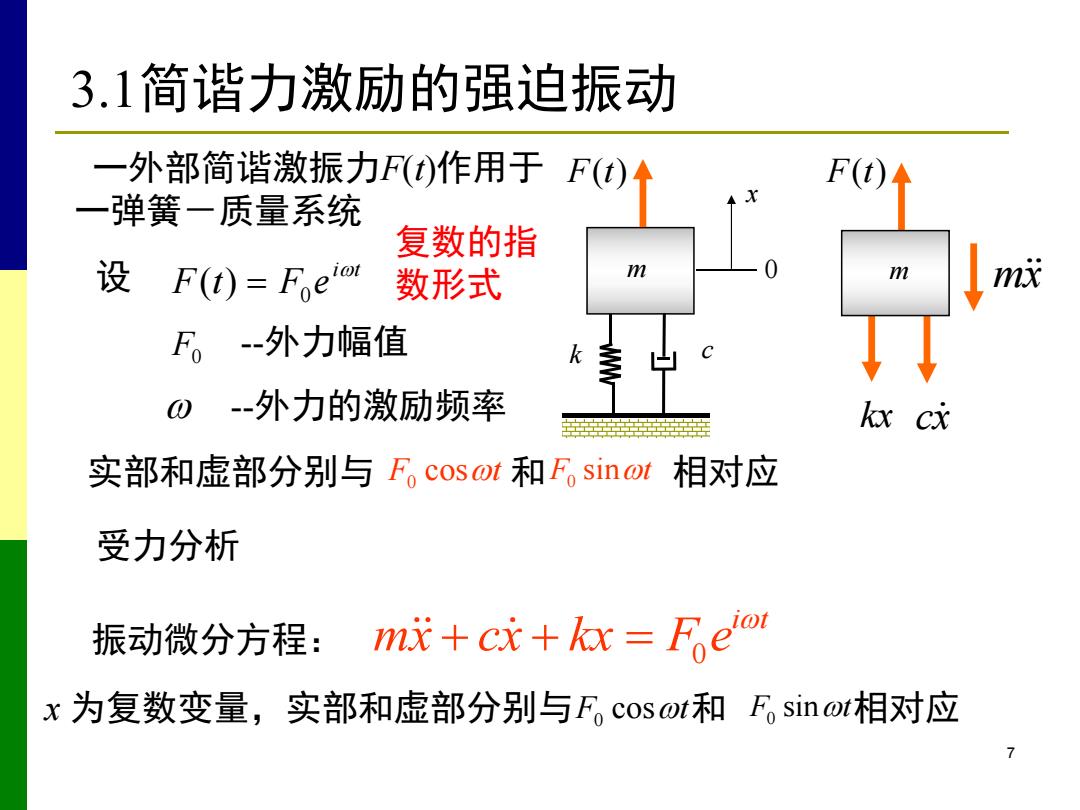
3.1简谐力激励的强迫振动 一外部简谐激振力F(t)作用于F(t)A F(t 一弹簧一质量系统 复数的指 设F(t)=Feo 数形式 F。外力幅值 k -外力的激励频率 kx cx 实部和虚部分别与F。cos@t和Fo sinwt相对应 受力分析 振动微分方程： m成+cx+kx=Feo x为复数变量，实部和虚部分别与F。cos@t和F。sinwt相对应

7 3.1简谐力激励的强迫振动 一外部简谐激振力F(t)作用于 一弹簧－质量系统 设 i t F t F e  0 ( )  F0 --外力幅值  --外力的激励频率 0 i t mx cx kx F e  振动微分方程：     F cost x 为复数变量，实部和虚部分别与 0 和 F0 sint相对应 实部和虚部分别与 F0 cost 和F0 sint 相对应 m cx mx kx F(t) 受力分析 k c x m 0 F(t) 复数的指 数形式

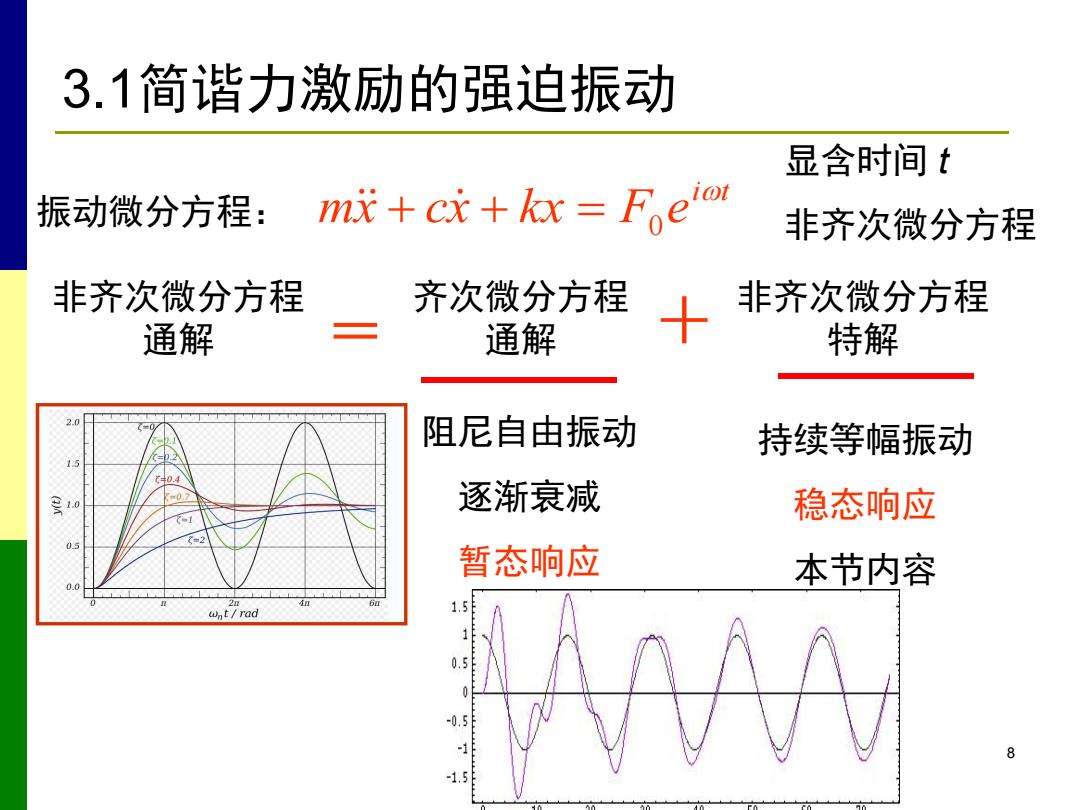
3.1简谐力激励的强迫振动 显含时间t 振动微分方程： mi+ci+kx=Foelo 非齐次微分方程 非齐次微分方程 齐次微分方程 非齐次微分方程 通解 通解 特解 阻尼自由振动 持续等幅振动 逐渐衰减 稳态响应 C=2 暂态响应 本节内容 wt/rad 1.5 0.5 -0.5 -1 8 -1.5

8 i t mx cx kx F e     0 振动微分方程：   显含时间 t 非齐次微分方程 阻尼自由振动 逐渐衰减 暂态响应 持续等幅振动 稳态响应 本节内容 非齐次微分方程 通解 齐次微分方程 通解 非齐次微分方程 ＝ ＋ 特解 3.1简谐力激励的强迫振动

3.1简谐力激励的强迫振动 振动微分方程：m成十Ccx+=Fe 设特解：x=xeo x：稳态响应的复振幅 代入振动微分方程，有： X=H(@)Fo 1 H(o)= k-mo2 +ico 复频响应函数 k 0n= m 5= 2/km 振动微分方程可变为：戈+250nc+0x=Boe F B 静变形 k 9

9 i t mx cx kx F e     0 振动微分方程：   设特解： i t x xe   代入振动微分方程，有： 0 x  H()F 2 1 H( ) k m ic       复频响应函数 m k n  2 c km   x ：稳态响应的复振幅 振动微分方程可变为： 2 2 2         i t n n n x x x B e k F B 0  静变形 3.1简谐力激励的强迫振动

3.1简谐力激励的强迫振动 振动微分方程： +250+@x=Boieim 3-H()Fs H(0)=k-mo+ico 0 引入：S= 则：Ho)= 1-s2-25s0 1 B(s)= V1-s2)2+(25s)2 06)=g2 -52 振幅放大因子 相位差 因为x=xeio X三 Fo Bei(o-0)=Aei(o-0) k 10 A=BB 稳态响应的实振幅

10 引入： n s    2 2 2 2 1 1 2 ( ) [ ] (1 ) (2 )         s si H k s s 2 2 2 1 ( ) (1 ) (2 )      s s s 1 2 2 ( ) 1      s s tg s 振幅放大因子 相位差 则：   i e k   1 振动微分方程： 2 2 2 i t n n n x x x B e         0 x  H()F    k m ic H    2 1 ( ) 0 (  )    i t e k F x A  B 稳态响应的实振幅 (  )  i t Ae 3.1简谐力激励的强迫振动 i t x xe  因为 