第五章电磁感应与磁场能量 本章目录: d §5.1法拉第电磁感应定律 §5.2电感的定义与计算 §5.3磁场的能量 跑来跑去的科拉顿
§5.1 法拉第电磁感应定律 §5.2 电感的定义与计算 §5.3 磁场的能量 本章目录: 第五章 电磁感应与磁场能量

§5.1法拉第电磁感应定律 电磁感应现象 回路1 回路2 ①回路1接通或断开时,会在回路2上感应出瞬变电流; 当回路1成为电流恒定时,感应电流也消失 ②回路1载有恒定电流,但回路1相对于回路2有相对 运动或回路1运动,回路2静止,或回路2运动,回路1 静止,也会产生感应电流 ③永久性磁铁插入或抽出,若磁铁静止时,电路中没 有电流,插入或抽出的过程中会有电流
§5.1法拉第电磁感应定律 一、电磁感应现象 ①回路1接通或断开时,会在回路2上感应出瞬变电流; 当回路1成为电流恒定时,感应电流也消失。 ②回路1载有恒定电流,但回路1相对于回路2有相对 运动或回路1运动,回路2静止,或回路2运动,回路1 静止,也会产生感应电流。 ③永久性磁铁插入或抽出,若磁铁静止时,电路中没 有电流,插入或抽出的过程中会有电流。 回路1 回路2

§5.1法拉第电磁感应定律 法拉第把这些现象归结为:①回路的磁通量随时 间变化与否引起的②变化的磁通量在回路周围产 生一个感应电场,这个感应电场的环路积分就是 感生电动势。它的环路积分不为0,与静电场不同。 此时回路2上没有外加电源,只能认为感生电动势 是磁场引起,法拉第还进行了定量研究,得出了 感生电动势和磁通量随时间的变化率成正比。 dΦ dt
§5.1法拉第电磁感应定律 ~ d dt 法拉第把这些现象归结为:①回路的磁通量随时 间变化与否引起的②变化的磁通量在回路周围产 生一个感应电场,这个感应电场的环路积分就是 感生电动势。它的环路积分不为0,与静电场不同。 此时回路2上没有外加电源,只能认为感生电动势 是磁场引起,法拉第还进行了定量研究,得出了 感生电动势和磁通量随时间的变化率成正比

§5.1法拉第电磁感应定律 楞次确定了感生电动势的方向具有这样的规则: 感生电动势总是试图阻碍磁通量的变化。也就 是说,感生电动势产生感生电流,感生电流对 回路产生一个附加的磁通。这个磁通与原来的 磁通变化符号相反,削弱原来的磁通变化。 dΦ dt
§5.1法拉第电磁感应定律 楞次确定了感生电动势的方向具有这样的规则: 感生电动势总是试图阻碍磁通量的变化。也就 是说,感生电动势产生感生电流,感生电流对 回路产生一个附加的磁通。这个磁通与原来的 磁通变化符号相反,削弱原来的磁通变化。 d dt

§5.1法拉第电磁感应定律 ①回路静止,随时间变化 =EW=-5w=- ,ndS →V×E= OB ∮E.dl=∫V×Eas 8t ②回路以匀速运动,B不随时间变化 5-手E=Bns E的坐标随时间变化 运动坐标系 静止坐标系
§5.1法拉第电磁感应定律 l s s l s d B E dl B ndS ndS B dt t E t E dl E dS B ①回路静止, 随时间变化 ' ' l s d E dl B ndS E dt v B 的坐标随时间变化 ②回路以匀速 运动, 不随时 运动坐标系 静 间变化 止坐标系

§5.1法拉第电磁感应定律 ③回路以匀速运动,随时间变化 Bids 设ndS不随时间变化, 即回路以恒定速度运动,回路形状不变 dB B B dx @B dy OB dz dt B(x,y2,)= dt Ot Ox dt ay dt 8z dt +(F.V)B-OVx(BxF)+T(V.B) 8t 8t
§5.1法拉第电磁感应定律 ' ˆ ˆ , , , ( ) ( ) ( ) l s d E dl B ndS dt ndS v dB d B B dx B dy B dz B x y z t dt dt t x dt y dt z dt B B v B B v v B t v B t 设 不随时间 ③回路以匀速 运动, 随时间 变化, 即回路以恒定速度 运动,回路形状不变 变化

§5.1法拉第电磁感应定律 5=5ag+a ∮Edl=∫v×Eas →V×E' 、 +Vx(vxB) 8t 若 =0(即第二种情况)→V×E=V×(×B) 8t 第一种情况币=0,E=E→V×龙=- 6B 8t
§5.1法拉第电磁感应定律 ' ' ' ' ' ' ( ) ˆ 0 ( ) ( 0 ) l s l s B E v B E dl v B ndS t E dl E dS B E v B t B v E E t B E t 若 (即第二种情况) 第一种情况

§5.1法拉第电磁感应定律 我们要把它转回静止参考系,主要问题是不 同参考系的电场强度如何变换。 考虑到以下运动电荷所受的力 F=qE+qv×B=F=qE→E=E+v×B .☑×E= OB Ot 该方程是精确的,虽然伽利略不变性是近似 的,更严格的应用狭义相对论
§5.1法拉第电磁感应定律 我们要把它转回静止参考系,主要问题是不 同参考系的电场强度如何变换。 考虑到以 v 运动电荷所受的力 ' ' ' F qE qv B F qE E E v B B E t 该方程是精确的,虽然伽利略不变性是近似 的,更严格的应用狭义相对论
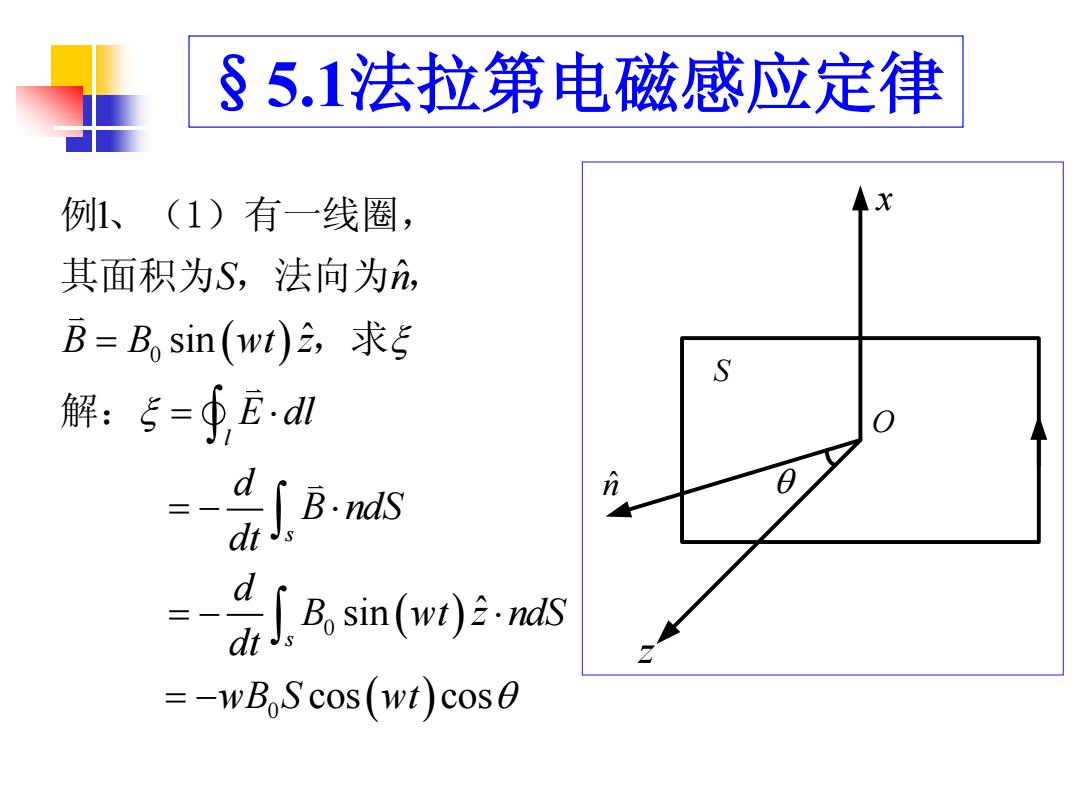
§5.1法拉第电磁感应定律 例1、(1)有一线圈, 其面积为S,法向为, B=B。sin(wt)含,求5 S 解:5=∮Ed 分 」马sn(a)ns =-wBoScos(wi)cos0
§5.1法拉第电磁感应定律 0 0 0 1 ˆ sin ˆ sin ˆ cos cos l s s S n B B wt z E dl d B ndS dt d B wt z ndS dt wB S wt 例 、(1)有一线圈, 其面积为 ,法向为 , ,求 解: O z x n ˆ S
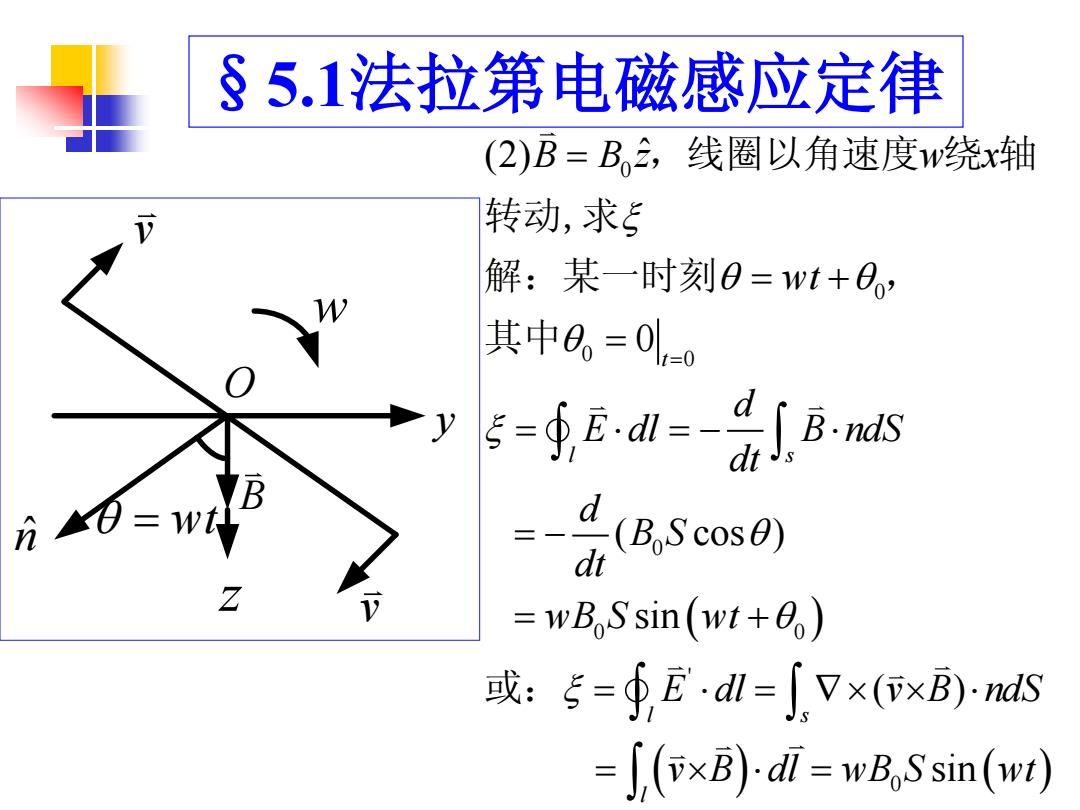
§5.1法拉第电磁感应定律 (2)B=B,三线圈以角速度w绕x轴 转动,求5 解:某一时刻0=wt+0o, 其中0。=0-0 5=手El=4ans B d(BScos0) Z =wBoSsin(wt+0) 或:5=∮E·dl=∫7x(xB)S =j(xB)cdi=wB,Ssin(w)
§5.1法拉第电磁感应定律 wt O z n ˆ y B v v w 0 0 0 0 0 0 0 ' 0 (2) ˆ 0 ( cos ) sin ( ) sin t l s l s l B B z w x wt d E dl B ndS dt d B S dt wB S wt E dl v B ndS v B dl wB S wt ,线圈以角速度 绕 轴 转动,求 解:某一时刻 , 其中 或: