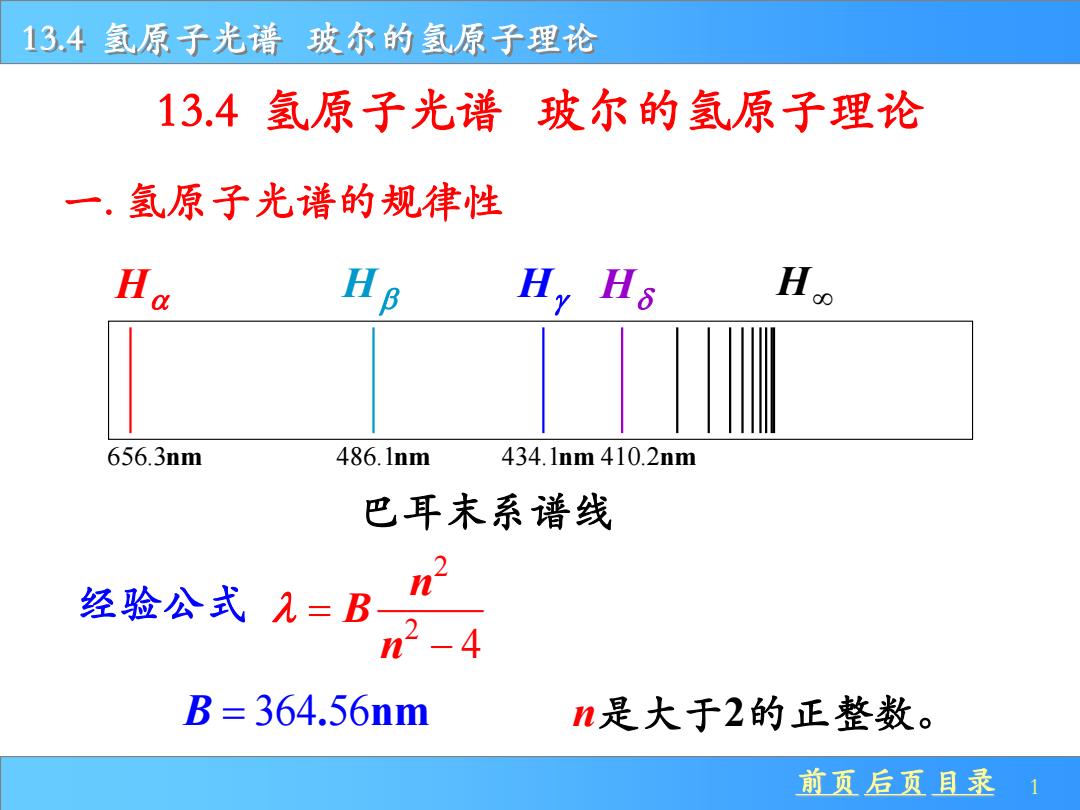
134氢原子光谱玻尔的氢原子理论 13.4氢原子光谱玻尔的氢原子理论 一.氢原子光谱的规律性 Ha H,Hs H 656.3nm 486.1nm 434.1nm410.2nm 巴耳末系谱线 经险公式AB” B=364.56nm n是大于2的正整数。 前页后页目录 1
前页 后页 目录 1 13.4 氢原子光谱 玻尔的氢原子理论 H H H H H 656.3nm 486.1nm 434.1nm 410.2nm 巴耳末系谱线 经验公式 2 2 4 n B n = − B = 364 56 . nm n是大于2的正整数。 一. 氢原子光谱的规律性 13.4 氢原子光谱 玻尔的氢原子理论

13.4氢原子光谱玻尔的氢原子理论 用频率表示v= 4c11 ΓB22n2 用波数表示V= 1y4,11 里德伯公式 k=1,2,3… n=k+1,k+2,k+3,… 里德伯常量R=1.096776×107m1 前页后页目录 2
前页 后页 目录 2 13.4 氢原子光谱 玻尔的氢原子理论 用频率表示 2 2 4 1 1 2 ( ) c B n = − 用波数表示 1 = 里德伯公式 2 2 1 1 R( ) k n = − 1 2 3 1 2 3 , , , , , , k n k k k = = + + + 里德伯常量 7 1 R 1 096 776 10 . m− = c = 2 2 4 1 1 2 ( ) B n = −

13.4氢原子光谱玻尔的氢原子理论 巴尔末系k=2,n=3,4,… 氢原子光谱各谱系的名称 k=1,n=2,3,…赖曼系,紫外区 k=3,n=4,5,…帕邢系,红外区 k=4,n=5,6,…布拉开系,红外区 k=5,n=6,7,…普丰德系,红外区 k=6,n=7,8,…哈弗莱系,红外区 原子光谱线系的规律性深刻地反映了原子内 部的规律性。 前页后页目录 3
前页 后页 目录 3 13.4 氢原子光谱 玻尔的氢原子理论 氢原子光谱各谱系的名称 k n = = 1 2 3 , , , 赖曼系,紫外区 k n = = 3 4 5 , , , 帕邢系,红外区 k n = = 4 5 6 , , , 布拉开系,红外区 k n = = 5 6 7 , , , 普丰德系,红外区 k n = = 6 7 8 , , , 哈弗莱系,红外区 原子光谱线系的规律性深刻地反映了原子内 部的规律性。 巴尔末系 k n = = 2 3 4 , ,

13.4氢原子光谱玻尔的氢原子理论 二.玻尔的氢原子理论 经典理论 原子核式结构模型 电磁辐射是连续光谱 玻尔理论的基本假设 1)定态假设 原子系统只能处在一系列不连续的能量状态。 在这些状态中,虽然电子作加速运动,但并不辐射 电磁波,这些稳定状态简称定态。 定态能量:E1,E2,E3,… 前页后页目录4
前页 后页 目录 4 13.4 氢原子光谱 玻尔的氢原子理论 二. 玻尔的氢原子理论 经典理论 原子核式结构模型 电磁辐射是连续光谱 玻尔理论的基本假设 1)定态假设 原子系统只能处在一系列不连续的能量状态。 在这些状态中,虽然电子作加速运动,但并不辐射 电磁波,这些稳定状态简称定态。 定态能量:E1,E2,E3,…

13.4氢原子光谱玻尔的氢原子理论 2)频率条件 原子从一个定态跃迁到另一个定态时,就要发 射或吸收一个光子。 En-Ek 玻尔频率公式 h 3)量子化条件 定态的角动量是量子化的 h L为轨道角动量 L=n n=1,2,3,… 2π n为量子数 前页后页目录 5
前页 后页 目录 5 13.4 氢原子光谱 玻尔的氢原子理论 2)频率条件 原子从一个定态跃迁到另一个定态时,就要发 射或吸收一个光子。 E E n k h − = 玻尔频率公式 3)量子化条件 定态的角动量是量子化的 2 , 1 2 3 π , , h L n = n = L为轨道角动量 n为量子数

13.4氢原子光谱玻尔的氢原子理论 三.氢原子轨道半径和能量的计算 电子绕核作圆周运动 e2 02 h =I- mor =n- 4π6or1 2π 上两式消去v,并把r改写为rn,得 n=1,2,3,… 元hme h=0.529×10-10m 玻尔半径 rn=n1n=1,2,3, 前页后页目录 6
前页 后页 目录 6 13.4 氢原子光谱 玻尔的氢原子理论 三. 氢原子轨道半径和能量的计算 电子绕核作圆周运动 2 2 2 0 4π e m r r = v 2π h m r n v = 上两式消去v,并把r改写为rn,得 2 2 0 2 ( ) , , , 1 2 3 π n h r n n m e = = 10 1 r . 0 529 10 m − = 玻尔半径 2 1 , , , 1 2 3 n r n r n = =
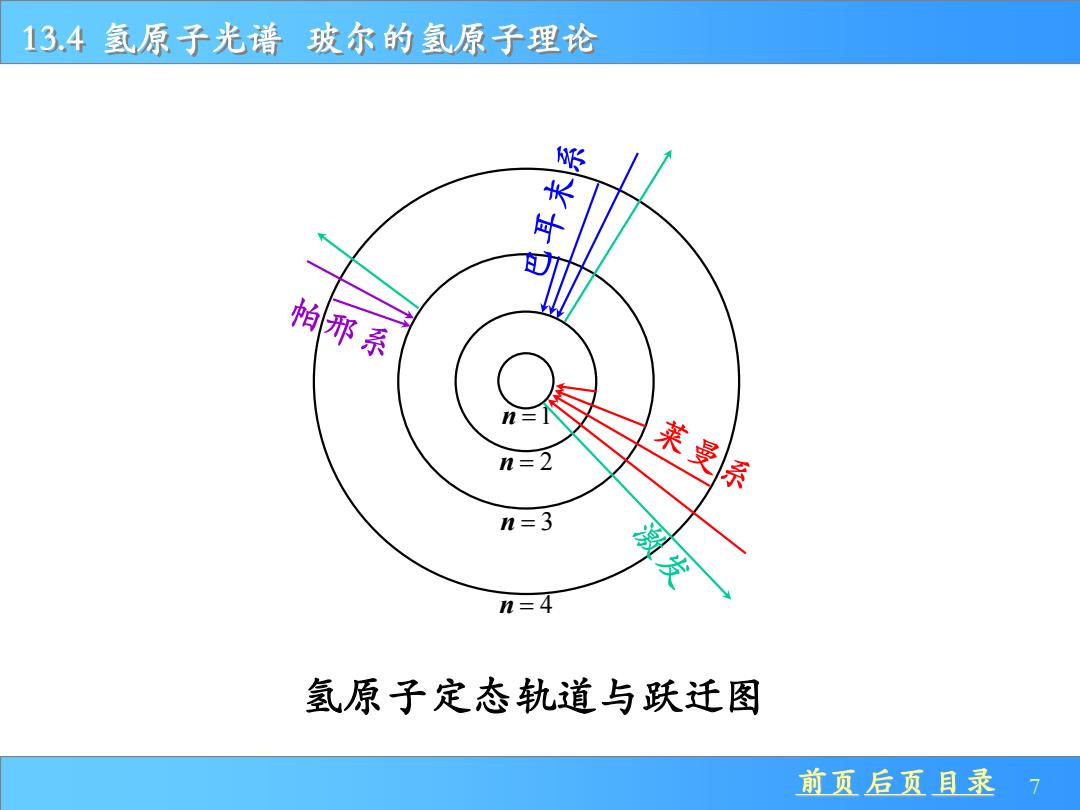
13.4氢原子光谱玻尔的氢原子理论 米 帕邢系 n=2 莱曼 n=3 n=4 氢原子定态轨道与跃迁图 前页后页目录7
前页 后页 目录 7 13.4 氢原子光谱 玻尔的氢原子理论 氢原子定态轨道与跃迁图 n =1 n = 2 n = 3 n = 4

13.4氢原子光谱玻尔的氢原子理论 氢原子系统能量 4π8o'n ò3 由于 4π8o'n 'a=n2(6oh2 氢原子能级 En=- me4 n=1,2,3,… 前页后页目录8
前页 后页 目录 8 13.4 氢原子光谱 玻尔的氢原子理论 氢原子系统能量 2 2 0 1 2 4π n n e E m r = − v 由于 2 2 2 0 4π n n e m r r = v 氢原子能级 4 2 2 2 0 1 1 2 3 8 ( ) , , , n m e E n n h = − = 2 2 0 2 ( ) π n h r n me =

13.4氢原子光谱玻尔的氢原子理论 En=- me4 22) n=1,2,3,. n2 880h 基态 n=1, E1=-13.58eV 受激态 n>1, En= E 1n→oo, Em→0能级趋于连续 电离态 E>0能级连续 前页后页且录9
前页 后页 目录 9 13.4 氢原子光谱 玻尔的氢原子理论 4 2 2 2 0 1 1 2 3 8 ( ) , , , n m e E n n h = − = 基态 受激态 n 1, , 0 n E → →n 能级趋于连续 电离态 E 0 能级连续 1 n 2 E E n = n =1, 1 E = −13 58 . eV
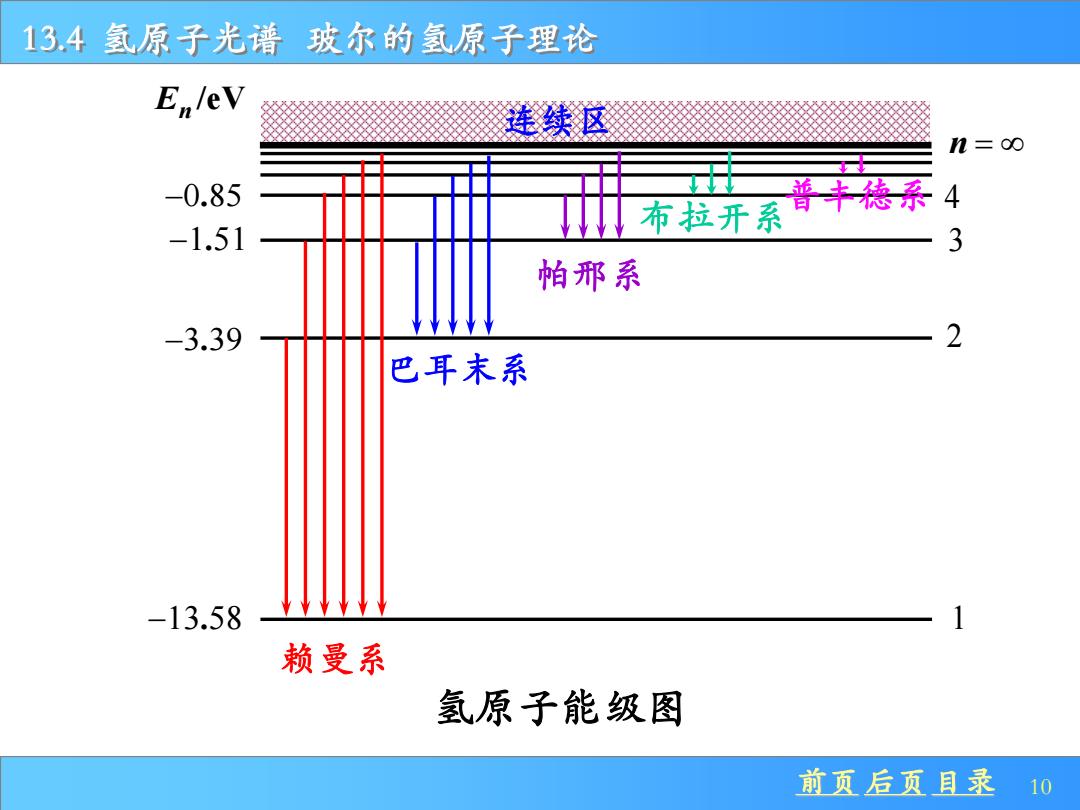
13.4氢原子光谱玻尔的氢原子理论 Elev 续区 n=o0 -0.85 T -1.51 T布拉开系 4 3 帕邢系 -3.39 巴耳末系 -13.58 赖曼系 氢原子能级图 前页后页目录、10
前页 后页 目录 10 13.4 氢原子光谱 玻尔的氢原子理论 赖曼系 巴耳末系 帕邢系 布拉开系普丰德系 1 2 4 3 n = En /eV −13 58 . −3 39 . −1 51 . −0 85 . 连续区 氢原子能级图