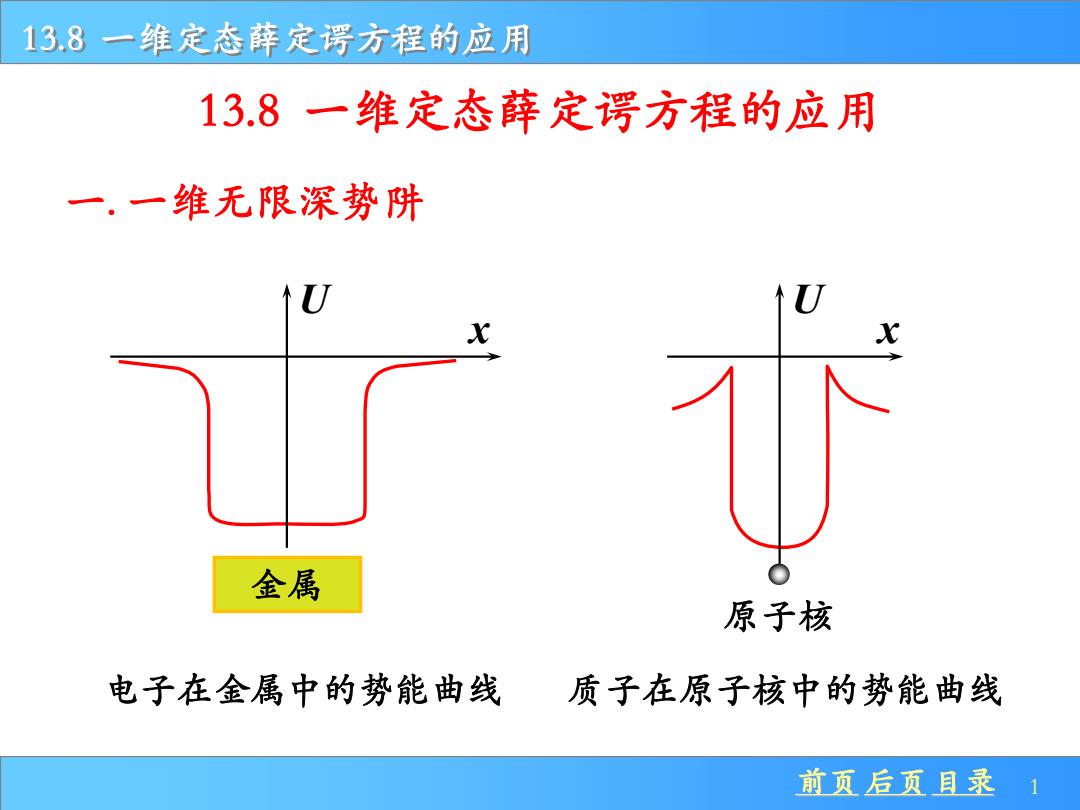
13.8一维定态薛定谔方程的应用 13.8一维定态薛定谔方程的应用 一.一维无限深势阱 金属 原子核 电子在金属中的势能曲线 质子在原子核中的势能曲线 前页后页目录 1
前页 后页 目录 1 13.8 一维定态薛定谔方程的应用 U x 金属 电子在金属中的势能曲线 U x 原子核 质子在原子核中的势能曲线 一. 一维无限深势阱 13.8 一维定态薛定谔方程的应用
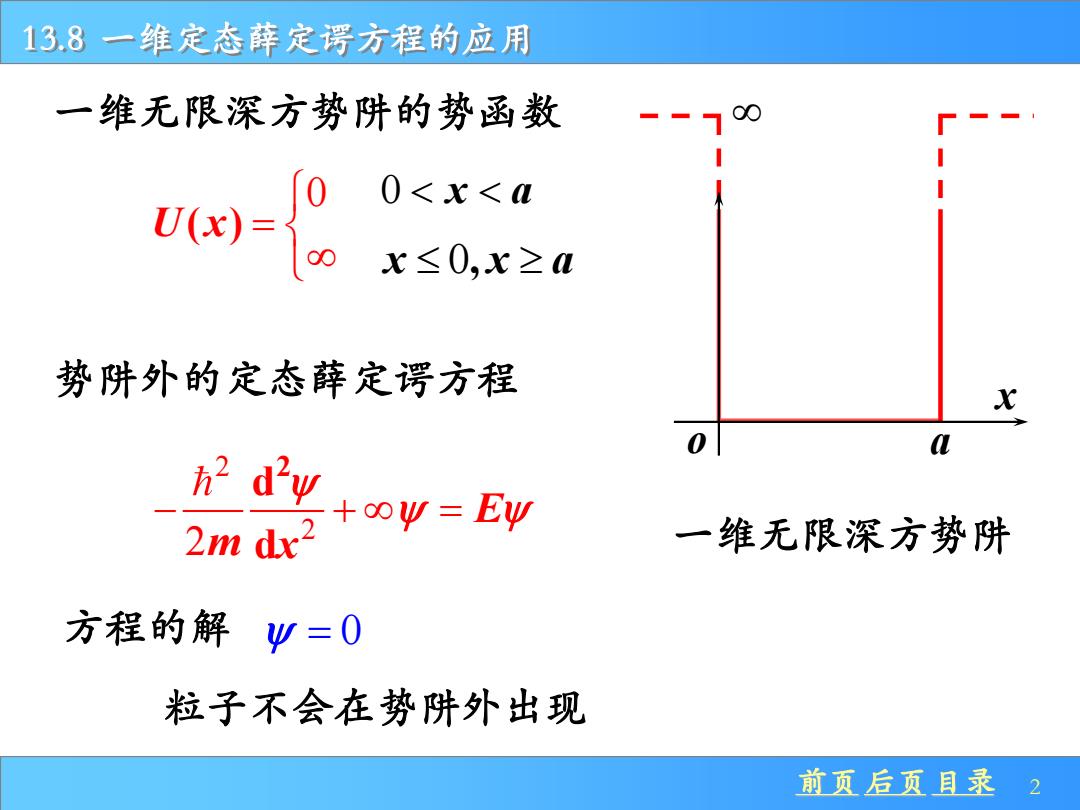
13.8一维定态薛定谔方程的应用 一维无限深方势阱的势函数 0 0<x<M U(x) 0 x≤0,x≥m 势阱外的定态薛定谔方程 0 h2 dw +oou=Eu 2m dx2 一维无限深方势阱 方程的解Ψ=0 粒子不会在势阱外出现 前页后页目录2
前页 后页 目录 2 13.8 一维定态薛定谔方程的应用 一维无限深方势阱 x o a 一维无限深方势阱的势函数 0 U x( ) = 0 x a x x a 0, 势阱外的定态薛定谔方程 2 2 2 2 d d E m x − + = = 0 粒子不会在势阱外出现 方程的解

13.8一维定态薛定谔方程的应用 势阱内的定态薛定谔方程 h2 d"w +0.w=Ew 2m dx2 令k2=2mE 方2 方程成为 kv-0 dr2 方程的解 y(x)=Csin(kx+δ) 前页后页目录 3
前页 后页 目录 3 13.8 一维定态薛定谔方程的应用 势阱内的定态薛定谔方程 2 2 0 2 2 d d E m x − + = 令 2 2 2mE k = 方程成为 2 2 0 2 d d k x + = 方程的解 ( ) sin( ) x C kx = +

13.8一维定态薛定谔方程的应用 w(x)=Csin(kx+8) 由边界条件定k和δ w(0)=0Csin6=0 6=0 y(a)=0 Csinka=0 k= ,n=1,2,3… W(x)=Csin n=12,3,.. 由归一化条件定C 前页后页目录 4
前页 后页 目录 4 13.8 一维定态薛定谔方程的应用 ( ) sin( ) x C kx = + 由边界条件定k和 ( ) 0 0 = Csin = 0 = 0 C ka sin = 0 1 2 3 π , , , n k n a = = 1 2 3 π ( ) sin , , , , n x C x n a = = 由归一化条件定C 2 0 ( ) d a x x ( ) a = 0 2 0 1 π sin d a n x C x a = =

13.8一维定态薛定谔方程的应用 得C= 2 所以(w)=Va sin- x,n=1,2,3,… 波函数表达式 E Ψ(x,t)= 二sin(x)eh,n=l,2,3,… 前页后页目录5
前页 后页 目录 5 13.8 一维定态薛定谔方程的应用 得 2 C a = 所以 2 1 2 3 π ( ) sin , , , , n x x n a a = = 波函数表达式 2 1 2 3 π ( , ) sin( )e , , , , i n Et Ψ x t x n a a − = =
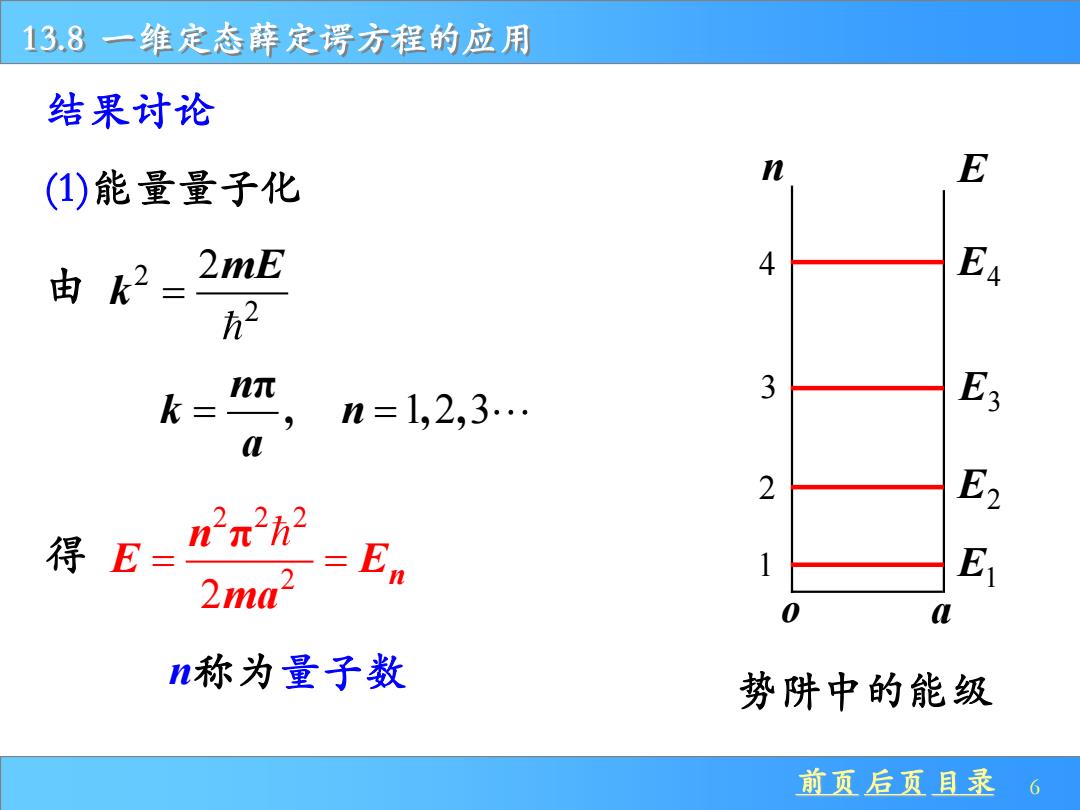
13.8一维定态薛定谔方程的应用 结果讨论 (1)能量量子化 E 由k2=2mE E 方2 k=mn 3 n=1,2,3… E E2 得E=nn2 2ma2=En E o n称为量子数 势阱中的能级 前页后页目录 6
前页 后页 目录 6 13.8 一维定态薛定谔方程的应用 结果讨论 (1)能量量子化 由 2 2 2mE k = 1 2 3 π , , , n k n a = = 得 2 2 2 2 2 π n n E E ma = = n称为量子数 E1 E2 E3 E4 o a n E 1 2 3 4 势阱中的能级

13.8一维定态薛定谔方程的应用 n2元2h2 En 2ma 能级的能量间隔 △E=Em+1-Em=(2n+l) π2h2 2 2m0 能级的能量相对间隔 △E(2n+1) →0 En n-→00 前页后页目录 7
前页 后页 目录 7 13.8 一维定态薛定谔方程的应用 能级的能量间隔 E E E = − n n +1 2 2 2 2 2 π n n E ma = 2 2 2 2 1 2 π ( ) n ma = + 能级的能量相对间隔 n E E 2 ( ) 2 1 n n + = 0 ⎯⎯⎯→ n→

13.8一维定态薛定谔方程的应用 n2π2h2 En= 2ma2 (②)最小能量不为零 E1= 元22 基态能或零点能 2ma (3)解为驻波形式 ,元 Et Ψ(x,t)= 二sin(x)eh,n=1,2,3,… 物质波在阱中形成驻波,阱壁处为波节。 前页后页目录8
前页 后页 目录 8 13.8 一维定态薛定谔方程的应用 (2)最小能量不为零 2 2 1 2 2 π E ma = 基态能或零点能 (3)解为驻波形式 物质波在阱中形成驻波,阱壁处为波节。 2 1 2 3 π ( , ) sin( )e , , , , i n Et Ψ x t x n a a − = = 2 2 2 2 2 π n n E ma =
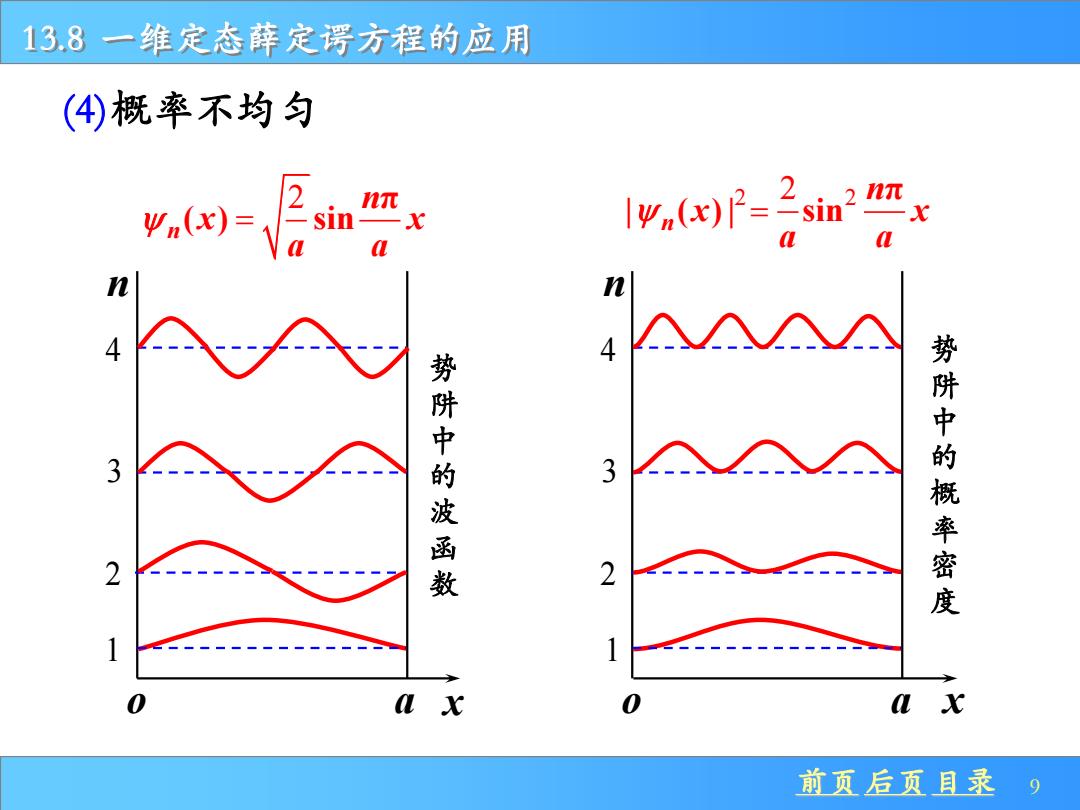
13.8一维定态薛定谔方程的应用 (4概率不均匀 2 Vn(x)= 1元 I(x)P-2sinx 色 4 4 势 势 阱 阱 中 中 的 3 的 概 数 2 密 a x 前页后页目录 9
前页 后页 目录 9 13.8 一维定态薛定谔方程的应用 (4)概率不均匀 o a n 1 2 3 4 2 π n ( ) sin n x x a a = 势 阱 中 的 波 函 数 x o a n 1 2 3 4 2 2 2 π | ( ) | sin n n x x a a = 势 阱 中 的 概 率 密 度 x

13.8一维定态薛定谔方程的应用 有限深势阱 粒子的能量又低于势壁,粒子在阱外不远处出 现的概率不为零。 (x)2 有 n 深势 中 --- 率分 布 前页后页目录 10
前页 后页 目录 10 13.8 一维定态薛定谔方程的应用 有限深势阱 粒子的能量又低于势璧,粒子在阱外不远处出 现的概率不为零。 o a n 1 2 3 2 | ( ) | n x 有 限 深 势 阱 中 的 概 率 分 布