
亲本2*大 第9章光的衍射 大雪物理A教章 ong Univereity of 第四篇 波动光学 第9章 光的衍射
第9章 光的衍射 大学物理A教案 第四篇 波动光学 第9章 光的衍射

(里度本2*大身 第9章光的衍射 大号物理A教素 光衍射 (1) 主要内容: ⊙光的衍射惠更斯-菲涅耳原理 ⊙单缝夫琅禾费衍射
第9章 光的衍射 大学物理A教案 光衍射(1) 主要内容: 光的衍射 惠更斯-菲涅耳原理 单缝夫琅禾费衍射

国上黄大避 第9章光的衍射 大号物理A表素 89.1惠更斯一 菲涅耳原理 惠更斯,C. 菲涅耳,A.-J
第9章 光的衍射 大学物理A教案 §9 1. 惠更斯 — 菲涅耳原理

盟廉本2黄大学 第9章光的衍射 大雪物理A教章 1、光的衍射现象 光偏离直线传播并且光强(光能)在空间不均匀分布 的现象叫光的衍射现象。 衍射现象产生的条件: 孔或障碍物的大小与 光波波长可以比拟。 说明: 若孔径与波长相比不是很大,那么屏上图象不再是均 匀的,而是明暗相间变化的条纹
第9章 光的衍射 大学物理A教案 1、光的衍射现象 光偏离直线传播并且光强(光能)在空间不均匀分布 的现象叫光的衍射现象。 衍射现象产生的条件: 孔或障碍物的大小与 光波波长可以比拟。 说明: 若孔径与波长相比不是很大,那么屏上图象不再是均 匀的,而是明暗相间变化的条纹

(里度本2*大皇 第9章光的衍射 大物A教素 2、惠更斯一 菲涅耳原理Huyghens--Fresnel principle) 惠更斯原理 波阵面上每一点可看成发射子波的新波源,其后任一 时刻,这些子波的包迹就构成新的波阵面。 能定性解释光的传播方向问题 菲涅耳用“子波相干叠加”的思想充实了惠原理,指 出:从同一波阵面上各点发出的子波在空间相遇时会产生 相干叠加,空间任一点的振动就是这些子波相干叠加的 结果。 惠更斯一菲涅耳原理 根据惠一菲原理,能定量解释衍射图样中光强分布不均 的问题
第9章 光的衍射 大学物理A教案 2、惠更斯 — 菲涅耳原理(H h uyg ens-F l i il) Fresnel principle) 惠更斯原理 波阵面上每一点可看成发射子波的新波源, 其后任一 时刻, 这些子波的包迹就构成新的波阵面。 菲涅耳用“子波相干叠加”的思想充实了惠原理 指 时刻, 这 子波的包 就构成新的波阵面 能定性解释光的传播方向问题 菲涅耳用“子波相干叠加”的思想充实了惠原理,指 出:从同一波阵面上各点发出的子波在空间相遇时会产生 相 叠加 空间任 点的振动就是这些子波相 叠加的 相干叠加,空间任一点的振动就是这些子波相干叠加的 结果。 惠更斯 菲涅耳原理 根据惠 — 菲原理, 能定量解释衍射图样中光强分布不均 —— 惠更斯 — 菲涅耳原理 根据惠 菲原理, 能定量解释衍射图样中光强分布不均 的问题

国桑水2黄大等 第9章 光的行射 大雪物理A教素 图中S为某一时刻的波阵面,它可 分割成无数面元(子波源)ds, 根据惠一菲原理,空间P点的光强 就是波阵面S上无数子波源发出的 子波在P点相干叠加的结果。 面元ds在P点引起的光振动可表为 dE=CK0cos 2 C为比例系数,K(O)为倾斜因子 积分上式可得整个波面S在P点产生的合振动 由于一般情况下这个积分不易计算,下面讨论衍射现象时将 采用另一种近似处理方法一菲涅耳半波带法
第9章 光的衍射 大学物理A教案 图中S为某 时刻的波阵面 它可 为某一时刻的波阵面,它可 分割成无数面元(子波源)ds, n 根据惠 菲原理 空间 ds P点的光强 S r P 根据惠 — 菲原理 , 空间P点的光强 就是波阵面S上无数子波源发出的 子波在P点相干叠加的结果。 面元ds在P点引起的光振动可表为 ) 2 ( ) ( dS r dE CK( ) cos( ) C为比例系数 K( )为倾斜因子 t r dE CK C为比例系数, K( )为倾斜因子 积分上式可得整个波面S在P点产生的合振动 dS r t r CK E P S ) 2 cos( ( ) ( ) 由于一般情况下这个积分不易计算,下面讨论衍射现象时将 采用另 种近似处理方法 一种近似处理方法 菲涅耳半波带法
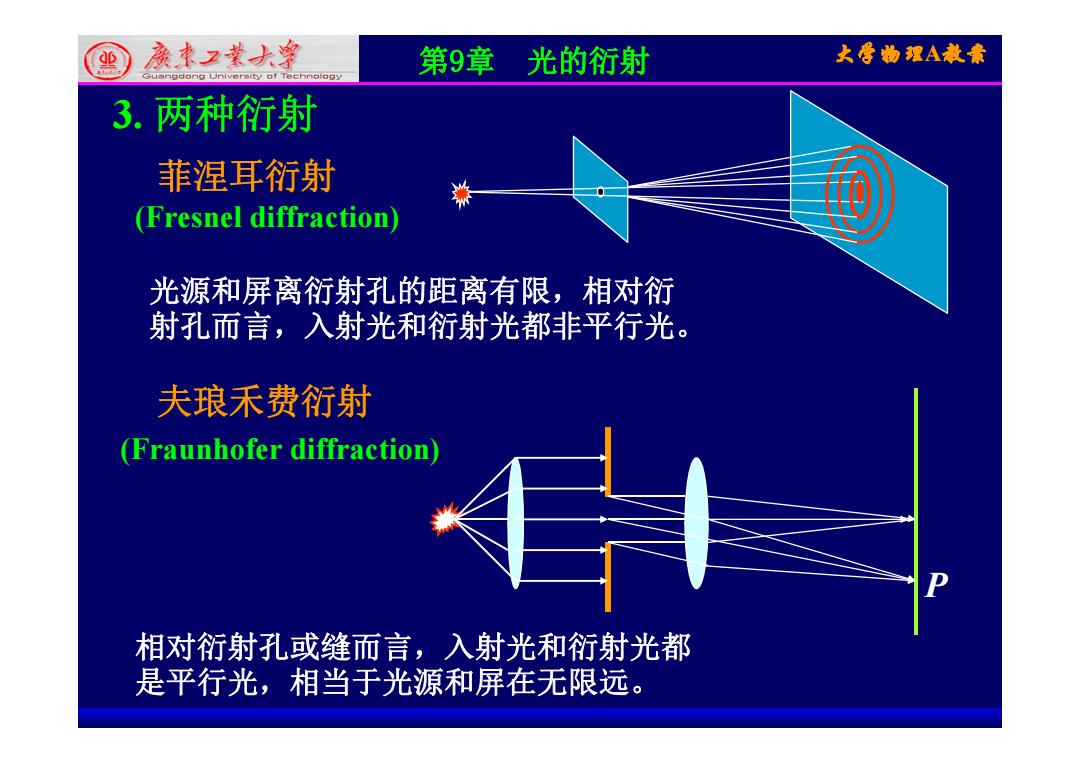
国藤本大 第9章光的衍射 大雪物理A教素 3.两种衍射 菲涅耳衍射 (Fresnel diffraction) 光源和屏离衍射孔的距离有限,相对衍 射孔而言,入射光和衍射光都非平行光。 夫琅禾费衍射 (Fraunhofer diffraction 相对衍射孔或缝而言,入射光和衍射光都 是平行光,相当于光源和屏在无限远
第9章 光的衍射 大学物理A教案 3. 两种衍射 菲涅耳衍射 (F l diff ti ) 光源和屏离衍射孔的距离有限,相对衍 (Fresnel diffraction) 光源和屏离衍射孔的距离有限,相对衍 射孔而言,入射光和衍射光都非平行光。 夫琅禾费衍射 (Fraunhofer diffraction) P 相对衍射孔或缝而言 入射光和衍射光都 相对衍射孔或缝而言,入射光和衍射光都 是平行光,相当于光源和屏在无限远

(但亲本2*大皇 第9章光的衍射 大号物理A教素 §9.2单缝夫琅禾费衍射 光源和观察屏都在距离衍射单缝无限远处。 单色光源 *(D一衍射光线与单缝法线的夹角(衍射角)(angle of difraction) *衍射孔到屏的距离等于透镜的焦距f。 为了讨论屏上P点的明暗,介绍菲涅耳波带法Fresnel zone construction)
第9章 光的衍射 大学物理A教案 §9 2. 单缝夫琅禾费衍射 单缝夫琅禾费衍射 光源和观察屏都在距离衍射单缝无限远处。 单色光源 P f 衍射光线与单缝法线的夹角(衍射角)(angle of difraction) * 为了讨论屏上 P 点的明暗,介绍菲涅耳波带法 (Fresnel * 衍射孔到屏的距离等于透镜的焦距 f 。 为了讨论屏 点的明暗 介绍菲涅耳波带法 ( zone construction)
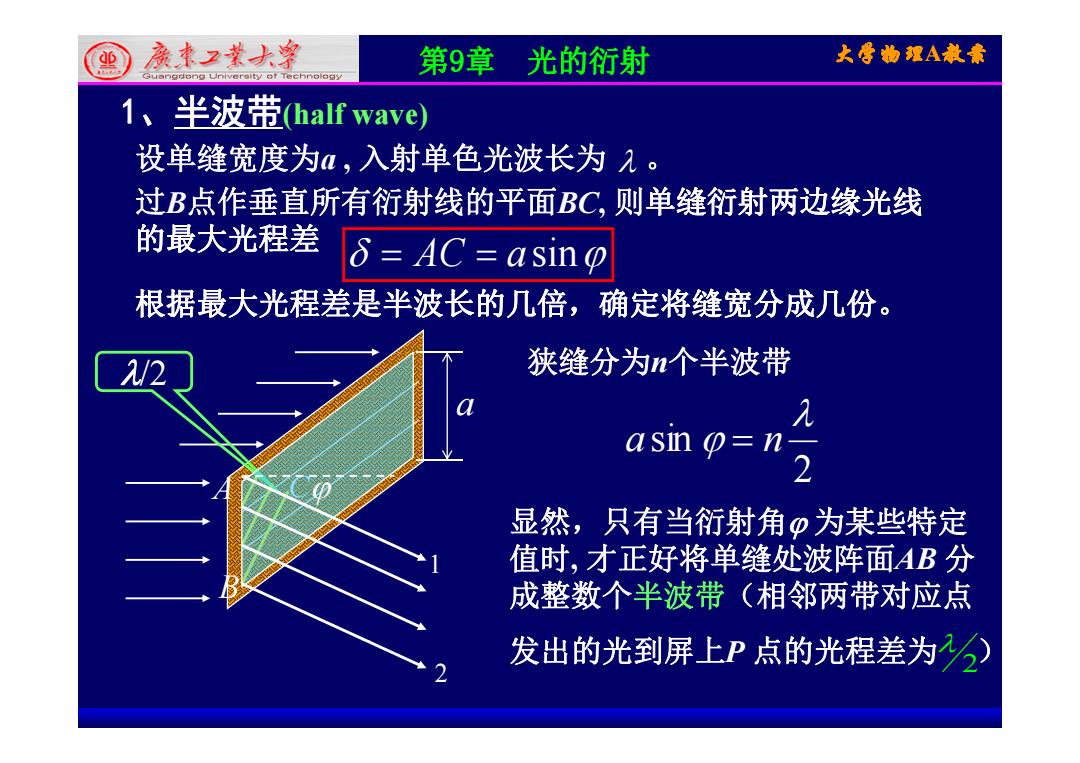
国亲本之大逢 第9章 光的行射 大学物理A教素 1、半波带half wave) 设单缝宽度为a,入射单色光波长为2。 过B点作垂直所有衍射线的平面BC,则单缝衍射两边缘光线 的最大光程差⑧=AC=asin 根据最大光程差是半波长的几倍,确定将缝宽分成几份。 狭缝分为n个半波带 aSn(Φ=n y 显然,只有当衍射角p为某些特定 值时,才正好将单缝处波阵面AB分 成整数个半波带(相邻两带对应点 发出的光到屏上P点的光程差为)
第9章 光的衍射 大学物理A教案 1、半波带(half wave) (half wave) 过B点作垂直所有衍射线的平面BC, 则单缝衍射两边缘光线 设单缝宽度为a , 入射单色光波长为 。 根据最大光程差是半波长的几倍 确定将缝宽分成几份 AC a sin 过B点作垂直所有衍射线的平面BC, 则单缝衍射两边缘光线 的最大光程差 根据最大光程差是半波长的几倍,确定将缝宽分成几份。 /2 狭缝分为n个半波带 a 2 sin a n /2 2 显然,只有当衍射角 为某些特定 值时 才正好将单缝处波阵面AB 分 A C 值时, 才正好将单缝处波阵面AB 分 成整数个半波带(相邻两带对应点 发出的光到屏上 点的光程差为 ) B 1 发出的光到屏上P 点的光程差为 2) 2

里)廉本2黄大¥ 第9章光的衍射 大雪物理A教素 衍射角P不同,AB波阵面能分 a 出的半波带数不同,半波带的个 数取决于单缝两边缘处行射线1、 2到屏上P点的光程差δ δ=AC=asin0 2、单缝衍射明暗条纹条件 (1)若4C=asing=2(
第9章 光的衍射 大学物理A教案 /2 衍射角 不同, AB波阵面能分 出的半波带数不同, 半波带的个 数取决于单缝两边缘处衍射线1、 a /2 数取决于单缝两边缘处衍射线1、 A C 2到 屏上P 点的光程差 AC a sin B 1 2 单缝衍射 暗条纹条件 A 2 2、单缝衍射明暗条纹条件 A a 2 c B (1)若 sin ( ) 2 2 AC a B