
恩身1:己知铜的摩尔质量M-位5g。密度P=89g©m3,在铜导线里,假设每一 个铜原子页献出一个自由电子,(1)为了技术上的姿全,副线内最大电流密度 ,=60A~m°,求此时铜线内电子的漂移速率,!(2)在室温下电子热运动的平均速率 是电子潭移速率,的多少倍? 题见1分析:一个副原子的质量m=MIN,·其中N,为阿伏伽德罗常数,由铜的密度P可 以推算出铜的原子数密度 是=P带 根据假设,每个■原子質献出一个自由电子,其电背为:,电流密度广。=。从而可 解得电子的潭移速率。· akT 将电子气祝为理想气体,根据气体动理论,电子热运动的平均速率下=】 其中业为被耳整曼常量,概,为电子质量。从而可解得电子的平均速率与潭移速率的关系。 解:《1)铜导线单位体积的原子数为 B=N、P/M 电流密度为。时铜线内电子的漂移速率 名"e/m■M/N度=446x10+m数 (2)室温下(T=30K)电子热运动的平均速率与电子漂移速率之比为 18&T =242x109 Fa Va imml 室温下电子热运动的平均建率远大于电子在稳恒电场中的定向源移速率。电子实际的运 动是无规热运动和沿电场相反方向的漂移运动的叠加,考虑到电子的漂移速率根小,电信号 的信息载体显然不会是定向潭移的电子。实验证明电信号是通过电磁液以光速传递的。 题头2:有两个同轴导体圆柱面,它门的长度均为20m,内圆柱面的半径为30mm,外圆柱 而的率径为9.0mm。若两圆柱面之间有10μA电流沿径向流过,求通过半径为60mm的圆 柱面上的电流密度, 思见2分析:如图所示,是同蛙桂面的横截面。电流密度/对中心 轴对称分布。积据稳恒电流的连线性,在两个同轴导体之间的任 意一个半径为?的同轴圆柱而上流过的电流!都相等,因此可得 1=1/2aL 解:由分析可知,在半径F=60mm的网柱面上的电流密度 /=112l-13站×10*Am 思见3:有两个半径分别为R和R:的同心球壳.其阿充满了电导半为y(y为常量)的介质, 若在两球壳维持恒定的电势差U。求两球壳间的电流。 恩见3分析:可采用两种方法求解,(1》根据欧婚定律的微分形式j=E和电流/一了S。 球壳间的电场分布应为球时珠。但设内、外球壳分别均匀带电荷0,则球壳间的电场强度 ”量可,两球壳的电势差 E
题 9.1:已知铜的摩尔质量 1 63.75 g mol − M = ,密度 3 8.9 g cm− = ,在铜导线里,假设每一 个铜原子贡 献出一 个自由 电子,( 1)为 了技术上 的安全 ,铜线 内最大电 流密度 2 m 6.0 A mm− j = ,求此时铜线内电子的漂移速率 d v ;(2)在室温下电子热运动的平均速率 是电子漂移速率 d v 的多少倍? 题 9.1 分析:一个铜原子的质量 A m = M / N ,其中 NA 为阿伏伽德罗常数,由铜的密度 可 以推算出铜的原子数密度 n = / m 根据假设,每个铜原子贡献出一个自由电子,其电荷为 e ,电流密度 m nevd j = 。从而可 解得电子的漂移速率 d v 。 将电子气视为理想气体,根据气体动理论,电子热运动的平均速率 e 8 m kT v = 其中 k 为玻耳兹曼常量, me 为电子质量。从而可解得电子的平均速率与漂移速率的关系。 解:(1)铜导线单位体积的原子数为 n = N A / M 电流密度为 m j 时铜线内电子的漂移速率 4 1 d m m A / / 4.46 10 m s − − v = j ne = j M N e = (2)室温下( T = 300K )电子热运动的平均速率与电子漂移速率之比为 8 d d e 2.42 10 1 8 = m kT v v v 室温下电子热运动的平均速率远大于电子在稳恒电场中的定向漂移速率。电子实际的运 动是无规热运动和沿电场相反方向的漂移运动的叠加。考虑到电子的漂移速率很小,电信号 的信息载体显然不会是定向漂移的电子。实验证明电信号是通过电磁波以光速传递的。 题 9.2:有两个同轴导体圆柱面,它们的长度均为 20 m ,内圆柱面的半径为 3.0 mm ,外圆柱 面的半径为 9.0 mm。若两圆柱面之间有 10μA 电流沿径向流过,求通过半径为 6.0 mm 的圆 柱面上的电流密度。 题 9.2 分析:如图所示,是同轴柱面的横截面。电流密度 j 对中心 轴对称分布。根据稳恒电流的连续性,在两个同轴导体之间的任 意一个半径为 r 的同轴圆柱面上流过的电流 I 都相等,因此可得 j = I / 2rL 解:由分析可知,在半径 r = 6.0 mm 的圆柱面上的电流密度 5 2 / 2 1.33 10 A m − − j = I rL = 题 9.3:有两个半径分别为 R1 和 R2 的同心球壳。其间充满了电导率为 ( 为常量)的介质, 若在两球壳间维持恒定的电势差 U 。求两球壳间的电流。 题 9.3 分析:可采用两种方法求解,(1)根据欧姆定律的微分形式 j = E 和电流 = j dS I 。 球壳间的电场分布应为球对称。假设内、外球壳分别均匀带电荷 Q ,则球壳间的电场强度 2 r 4 0 r E e r Q = ,两球壳的电势差

U=E山 另外球壳间的电瓷常度/沿径向且在球面上均匀分布,因此,两球壳间的电流 1-d4sj小4o 由上述关系可解得两球壳问的径向电流, (2)在求得球壳同径向电阻的基础上,由欧湖定律求球壳间的径向电流,在介质中任 取一同心球壳作微元。球壳面积为灯,厚度为,依照电阻的定义。该微元内、外表面 间的电阻 id山 dR - y 4u 导体球壳间的总电阻R一仪织。再由做鳄定律求出径向电流 解1:假授内、外球壳分别带电士Q,两球壳间的电势差 U-JE.dr-2(11) 4罩6民儿 球壳同的电流强度 1=fi-d5yE4w2'=4成8 民一R 解2:导体球壳间的总电阻 培片 由以姆定律,径向电流强度 1-'.4R尾 R R2-R 题9,和同样粗饵的碳棒和铁棒串联。能使两棒的总电阻不随温度而变化。问此时两棒的长 度比应为多少? 解,设室温下两棒的电阻分别为R和尾.·温度改变△T后电阻分别为 元=R1+a△刀 =R.0+△T) 式中:和:.分别为蜜温时碳和铁的电阻温度系数,查表得碳和铁的电阳率和电阅温度系数 分别为 4=35x1030-m1=-5×10K A.=10x10-'0mGe=50x10K 依照题意,串联后的总电阻不随盟度改变,故有 Rtte +Ryne =0 又根据电阳的定义R-P了·在两导线极面相同的条件下,则有 kf=a4./ack=2.86×10 恩见5:如图所示,载圆锥体的电阻率为P。长为,两端面的半径分别为风和R,。试计算 此锥体两编南之间的电阻:
= 2 1 d R R U E r 另外球壳间的电流密度 j 沿径向且在球面上均匀分布,因此,两球壳间的电流 2 I = d = j 4r j S 由上述关系可解得两球壳间的径向电流。 (2)在求得球壳间径向电阻的基础上,由欧姆定律求球壳间的径向电流。在介质中任 取一同心球壳作微元,球壳面积为 2 4r ,厚度为 dr ,依照电阻的定义,该微元内、外表面 间的电阻 2 4 1 d d r r R = 导体球壳间的总电阻 = 2 1 d R R R R 。再由欧姆定律求出径向电流。 解 1:假设内、外球壳分别带电 Q ,两球壳间的电势差 ) 1 1 ( 4 d 0 r 1 2 2 1 R R Q U R R = = − E r 球壳间的电流强度 2 1 2 4 1 2 d 4 R R U R R I r − = = = j S E 解 2:导体球壳间的总电阻 ) 1 1 ( 4 1 4 1 d 1 2 2 2 1 r R R r R R R = = − 由欧姆定律,径向电流强度 2 1 4 1 2 R R U R R R U I − = = 题 9.4:同样粗细的碳棒和铁棒串联,能使两棒的总电阻不随温度而变化。问此时两棒的长 度比应为多少? 解:设室温下两棒的电阻分别为 RC 和 RFe ,温度改变 T 后电阻分别为 (1 ) (1 ) Fe Fe Fe C C C R R T R R T = + = + 式中 C 和 Fe 分别为室温时碳和铁的电阻温度系数,查表得碳和铁的电阻率和电阻温度系数 分别为 3 1 C 7 1 Fe 4 1 C 5 1 C 1.0 10 m 5.0 10 K 3.5 10 m 5 10 K − − − − − − − = = = = − ; ; 依照题意,串联后的总电阻不随温度改变,故有 RC C + RFeFe = 0 又根据电阻的定义 S l R = ,在两导线截面相同的条件下,则有 2 C / Fe Fe Fe / C C 2.86 10 − l l = − = 题 9.5:如图所示,截圆锥体的电阻率为 ,长为 l ,两端面的半径分别为 R1 和 R2 。试计算 此锥体两端面之间的电阻

(a】 (b) 恩男5分新:对于相细不均匀导体的电阻,不能直接用R一计算。垂直于推体轴线线取 一半径为r,厚为d的微元,此微元电阻4R=P 。·沿轴线对元电阻R积分,即得总电 IR-了dR, 解:由分析可得锥体两端面间的电阻 R-lo (1) 由儿何关系呵得 x/1=(r-R)民-是) 则 血“R-R (2) 将式(2)代人式(1)得 g产品 思96:一同轴电规,其长L=1.5×10'm,内导体外径及=10m,外导体内径凡=50m, 中间填充绝缘介质。由干电爱受湘,测得绝缘介质的电阳率降低到64×0口m,若信号潭 是电动势c-24V,内阻R-3.0Q的直流电源,求在电黄末端的典找电阳及=1.00上的信 号电压为多大? ) , 恩96分析:由于电烫受潮,同轴电境内、外导体间存在径向漏电电阻R,它与负载电阻R 构成并联电路。其等效电路图如图所示。根据全电路欧舞定律可求出负载上的信号电压。 解:同轴电境的径白漏电电阻
题 9.5 分析:对于粗细不均匀导体的电阻,不能直接用 S l R = 计算。垂直于锥体轴线截取 一半径为 r 、厚为 dx 的微元,此微元电阻 2 d d r x R = ,沿轴线对元电阻 dR 积分,即得总电 阻 R = dR 。 解:由分析可得锥体两端面间的电阻 = 2 d r x R (1) 由几何关系可得 / ( ) /( ) R2 R1 R2 x l = r − − 则 r R R l dx d 1 − 2 = (2) 将式(2)代人式(1)得 1 2 2 1 2 d ( ) 1 2 R R l r r R R l R R R = − = 题 9.6:一同轴电缆,其长 1.5 10 m 3 L = ,内导体外径 R1 =1.0 mm ,外导体内径 R2 = 5.0 mm , 中间填充绝缘介质。由于电缆受潮,测得绝缘介质的电阻率降低到 6.4 10 m 5 。若信号源 是电动势 = 24 V ,内阻 Ri = 3.0 Ω 的直流电源,求在电缆末端的负载电阻 R0 =1.0 kΩ 上的信 号电压为多大? 题 9.6 分析:由于电缆受潮,同轴电缆内、外导体间存在径向漏电电阻 R ,它与负载电阻 R0 构成并联电路,其等效电路图如图所示。根据全电路欧姆定律可求出负载上的信号电压。 解:同轴电缆的径向漏电电阻

R-已h 2 R 它与负载电阻并联后的总电凰为 R-RR-9%50 R+R 由全电路的威等定律G=∑(R"+),可得负载上的信号电压 U=RI=RE =233V R'+r 比较电凌受海前后负载的端电压,可知电压下降了07V, 题.方有一平板电容卷,其电容C=1.DF,极板间介质的电阳率P=20×0~m,相对 电容率云,=5.0,求该电容器两极间的电阻值。 题9.7解:根据电阻的定义,两极板间的电阻 而充裤均匀介质的平板电容器,其电容C-SC5,1d,由上述两式可得 R=p55=85×10'n 恩8:如图所示,在两挠薄桐板之间,放置内、外半径分别为片和乃的环形硅, 5=0.80cm5=30em=50em,如在两极何如200V的电势差,求电路中的电流. 恩9.8解:根暴电阻的定久,环形硅的电阻 R-P -n) 查表知硅的电阻率少=6.4×100·m,在相定电压 U的作用下,硅中的电流为 1=号=-2U=164x10A=64mA R N 题复身:在相距15m的A、B两地之间地下,铺设有一条双般电俊,其中一根导线因某处 绝缘层破损触地而发生故障。检修人员用图所示装置可找出截障点位置。该装置中 元=200x0',R为可变电钮。现通知A地工作人员将该对电烫短接,测得检流计G没有 电瓷时电阻R=1新×10'0。求电领损坏处到B的距离x。(电须每千米直流阻航为150Q) (b)
1 2 ln 2 R R L R = 它与负载电阻并联后的总电阻为 = + = 98.5 0 0 R R R R R 由全电路的欧姆定律 =I(R+ r) ,可得负载上的信号电压 = 23.3 V + = = R r R U R I 比较电缆受潮前后负载的端电压,可知电压下降了 0.7 V。 题 9.7:有一平板电容器,其电容 C =1.0 μF ,极板间介质的电阻率 2.0 10 Ω m 13 = ,相对 电容率 r = 5.0 ,求该电容器两极间的电阻值。 题 9.7 解:根据电阻的定义,两极板间的电阻 S d R = 而充满均匀介质的平板电容器,其电容 C = S 0 r / d ,由上述两式可得 8.85 10 Ω 0 r 8 = = C R 题 9.8:如图所示,在两块薄铜板之间,放置内、外半径分别为 1 r 和 2 r 的环形硅, r1 = 0.80 cm, r2 = 3.0 cm, h = 5.0 cm ,如在两极间加 200 V 的电势差,求电路中的电流。 题 9.8 解:根据电阻的定义,环形硅的电阻 ( ) 2 1 2 2 r r h R − = 查表知硅的电阻率 6.4 10 Ω m 2 = ,在恒定电压 U 的作用下,硅中的电流为 1.64 10 A 16.4 mA ( ) 2 2 1 2 2 = = − = = − U l r r R U I 题 9.9:在相距 15.0km 的 A 、 B 两地之间地下,铺设有一条双股电缆,其中一根导线因某处 绝缘层破损触地而发生故障。检修人员用图所示装置可找出故障点位置。该装置中 R 2.00 10 Ω, R 3 0 = 为可变电钮。现通知 A 地工作人员将该对电缆短接,测得检流计 G 没有 电流时电阻 1.86 10 Ω 3 R = 。求电缆损坏处到 B 的距离 x 。(电缆每千米直流阻抗为 150 )
题9分析:以接地点P为分割点,将电线分成AP,PB两段,它们的电阻分别R,、R, 井与测试装置构成如图所示的电桥电路。当电桥平衡时(即检流计G内没有电流流过),有 (R+阶:R=尼R 由于R、R均与电领长度成正比。参题单位长度电境的直流电阻,可求得放障处到B的距 离¥。 解,设刀为单位长度电线线的直流电阻,L是A,B两地间的电缆长度,由电桥平衡条件 序+R=(2弘-M 解得 有=L-名=88m 题见1h:如图所示,号=号=20V,内阻尼=代=01且尼=500尾=4落0,试求:(1) 电落中的电流:(2》电落中消耗的功率:(3)两电源的端电压, 题身,10解:《1)由闭合电路的欧姆定律可得电路中的电流 6+6 -=0.4A 兄+兄+民+民 (2)电路中消耗的功率为 N=(民+昆+R,+R)-16W 《3)电源的端电压分别为 U,-写=脱=1.%V U2-马-R。-1.9%V 恩9.:在如图所示的电路中, 5=60V.6=20V,R=10n尾=20且R=30D.R,=4.00 求:(1)流过各电阻的电流:(2)A、B两点的电劳差U? 题9.1解:(1)取电流和回路绕行方付如图所示,由闭合电路欧姆定律,得 6-6 IR+民+R民+R =05A 蓬过各电阻的电流分别为 4-4-1=085A 人元108A 1=1-= 尼1=03为A 尼+R 《2)由一段含源电路的欧闻定律得 Ua=R=品=-52V
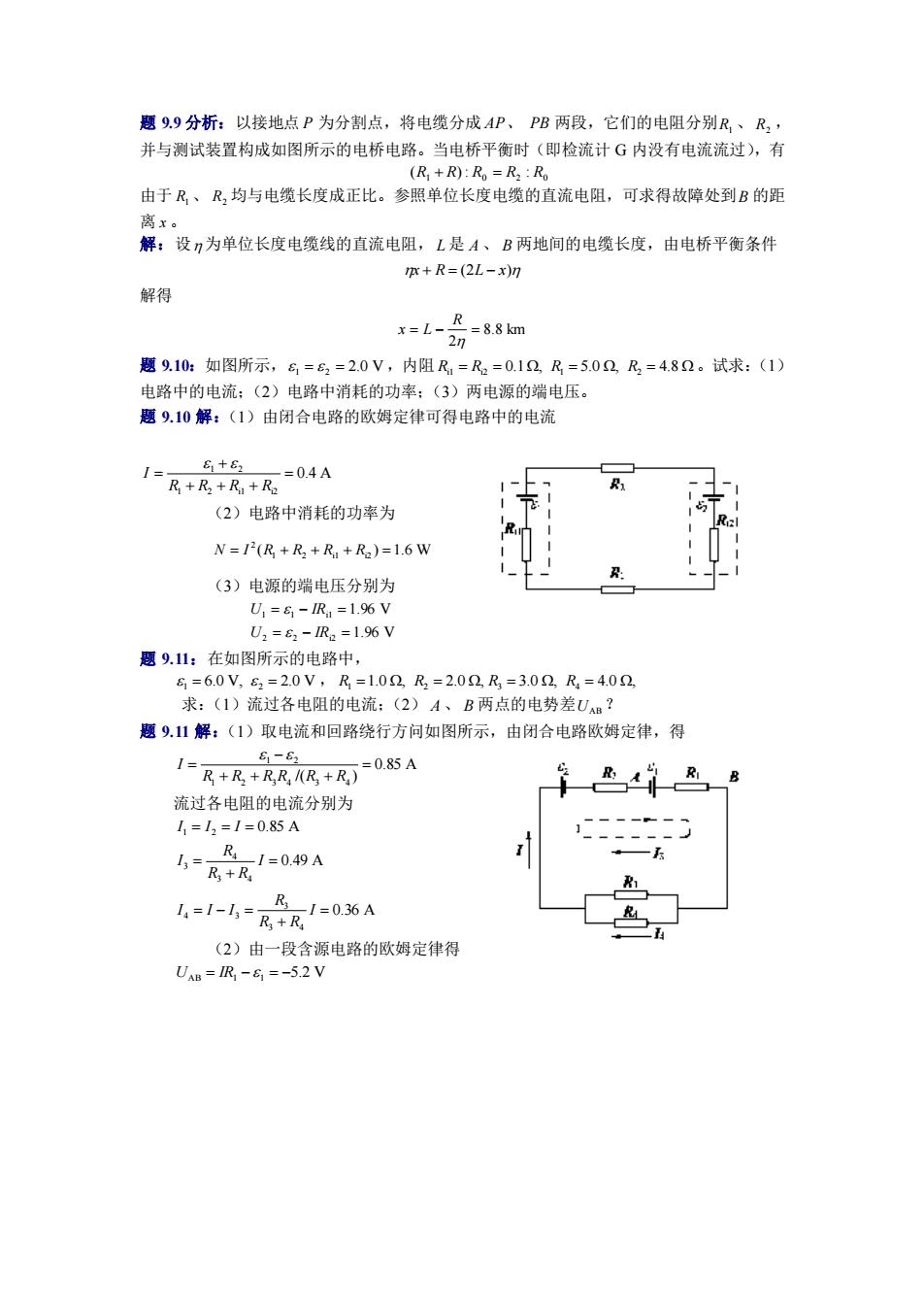
题 9.9 分析:以接地点 P 为分割点,将电缆分成 AP、 PB 两段,它们的电阻分别 R1 、 R2 , 并与测试装置构成如图所示的电桥电路。当电桥平衡时(即检流计 G 内没有电流流过),有 1 0 2 0 (R + R): R = R : R 由于 R1 、 R2 均与电缆长度成正比。参照单位长度电缆的直流电阻,可求得故障处到 B 的距 离 x 。 解:设 为单位长度电缆线的直流电阻, L 是 A 、 B 两地间的电缆长度,由电桥平衡条件 x + R = (2L − x) 解得 8.8 km 2 = − = R x L 题 9.10:如图所示, 1 = 2 = 2.0 V ,内阻 Ri1 = Ri2 = 0.1Ω, R1 = 5.0 Ω, R2 = 4.8 Ω 。试求:(1) 电路中的电流;(2)电路中消耗的功率;(3)两电源的端电压。 题 9.10 解:(1)由闭合电路的欧姆定律可得电路中的电流 0.4 A 1 2 i1 i2 1 2 = + + + + = R R R R I (2)电路中消耗的功率为 N = I 2 (R1 + R2 + Ri1 + Ri2 ) =1.6 W (3)电源的端电压分别为 1.96 V 1.96 V 2 2 i2 1 1 i1 = − = = − = U IR U IR 题 9.11:在如图所示的电路中, 1 = 6.0 V, 2 = 2.0 V , 1.0 Ω, 2.0 Ω, 3.0 Ω, 4.0 Ω, R1 = R2 = R3 = R4 = 求:(1)流过各电阻的电流;(2) A 、 B 两点的电势差 UAB ? 题 9.11 解:(1)取电流和回路绕行方问如图所示,由闭合电路欧姆定律,得 0.85 A /( ) 1 2 3 4 3 4 1 2 = + + + − = R R R R R R I 流过各电阻的电流分别为 I1 = I2 = I = 0.85 A 0.49 A 3 4 4 3 = + = I R R R I 0.36 A 3 4 3 4 3 = + = − = I R R R I I I (2)由一段含源电路的欧姆定律得 UAB = IR1 − 1 = −5.2 V