
6一1一打足气的自行车内胎,在7.0℃时,轮胎中空气的压强为4.0× 10的Pa,则当巡度变为37.0℃时,轮胎内空气的压强为多少?(设内胎容积 不变)》 分析胎内空气可桃为一定量的理想气体,其始末均为平衡态(即有骑定的 状态参量、VT值).由于气体的体积不变,由堕想气体物态方程pV=爱T 可知,压强中与祖度T成正比.由此即可求出末态的压强. 解由分析可知,当T2=37.0℃时,轮胎内空气压强为 p2≈T2p/T1=4.43×103Pa 可见当温度升高时,轮啪内气体压蓝变大,因此,夏季外出时自行车的车胎 不宜充气太足,以免爆胎

6一2在水面下S0.0m深的湖底处(湿度为4.0℃),有一个体积为1.0× 10-5m的空气泡升到湖面上来,若湖面的祖度为17.0℃,求气泡到达湖面的 体积.(农大气压强为=1.013×10Pa) 分析将气泡看成是一定量的理想气体,它位于湖底和上弃至湖面代表两 个不同的平衡状态.利用理想气体物态方程即可求解本愿.位于湖底时,气泡内 的压强可用公式p=0+g求出,其中p为水的春度(带取p=1,0×103 gm3). 解设气泡在潮底和颜面的状春参量分别为(p1,V1,T1)和(2,V2,T2). 由分析知湖底处压强为p1=2十gh=p0十Pgh.利用理想气体的物志方程可 得空气泡到达潮面的体积为 V2=pIT2 Vilp2T=(po+pgh)T2VilPoT =6.11×103m3

6-3辄气瓶的容积为3.2×10*2m3,其中氧气的压强为1.30×10?Pa,氧 气厂规定压强降到1.00×10Pa时,就应重新充气,以免经常洗瓶,某小型吹玻 璃车间,平均每天用去0.40m3压强为1.01×10Pa的氧气,问一瓶氧气能用多 少天?(设使用过程中温度不变) 分析由于使用条件的限制,瓶中氧气不可能完全被使用,为此,可通过两 条不同的思路进行分析和求解.(1)从氧气质量的角度来分析.利用理想气体物 态方程pV=mRTM可以分别计算出每天使用氧气的质量m3和可供使用的 氧气总质量(即原瓶中氧气的总质量m1和需充气时瓶中剥余氧气的质量m2 之差),从而可求得使用天数n=(1~2)/m3.(2)从容积角度来分析.利用 等温影胀条件将原瓶中氧气由初态(p1=1.30×10?Pa,V,=3.2×10-2m)影 张到需充气条件下的终态(p2=1.00×10Pa,V2待求),比较可得2状态下实 际使用掉的氧气的体积为V2一V1.同样将每天使用的氧气由初态(p3=1.01× 10Pa,V3=0.4m)等祖压缩到压强为2的终态,并算出此时的体积V2,由此 可得使用天数应为n=(V2-V,/V2 解1根据分析有 m1兰M电1V/RT:m2=Mp2V1/RT;m3=Mp3V3/RT 则一瓶氧气可用天数 n=(m1-m2/m3=(p1-2)V/p3V3 =9.5 解2根据分析中所述,由理想气体物态方程得等温影胀后瓶内氧气在压强 为p2=1.00×10的Pa时的体积为 V2 P1Vilp2 每天用去相同状态的氧气容积 V2=p3V3到p2 则瓶内氧气可用天数为 n =(V2-V1)/V2=(P1-p2)Vilps V3 =9.5

6一4位于委内骑拉的安转尔瀑布是世界上落差最大的深布,它高979m. 如果在水下落的过程中,重力对它所作的功中有50%转换为热量使水祖丹高, 求水由漫布顶部落到底部而产生的祖差.(水的此热容为4.18×103J·g-1· K-1) 分析取质量为的水作为研究对象,水从爆布顶部下落到底部过程中重 力作功W=gh,按题意,被水吸收的热量Q=0.5W,则水吸收热量后升高的 祖度可由Q=mc△T求得. 解 由上述分析得 c△T=0.5mgh 水下落后升高的温度 ΔT=0.5gh1c=1.15K
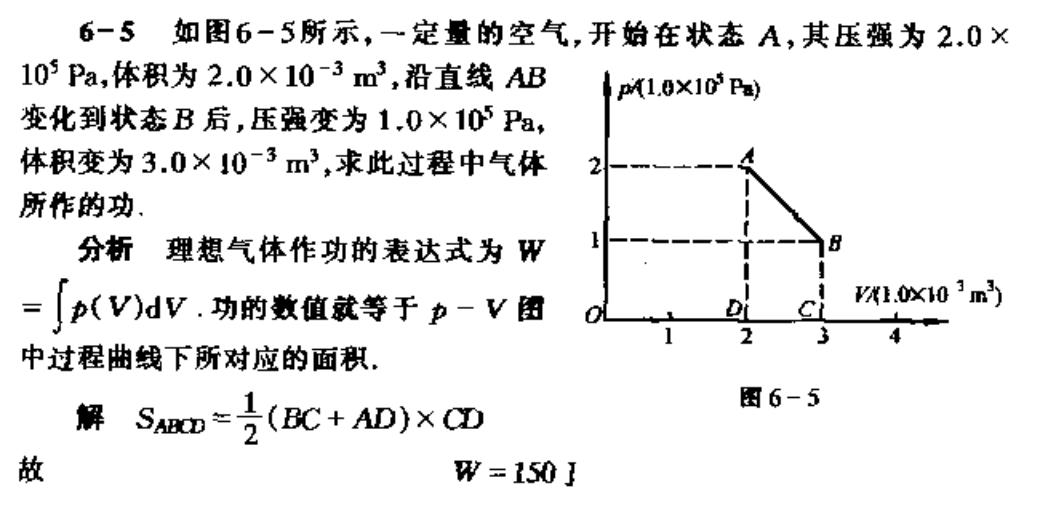
6-5如图6-5所示,一定量的空气,开始在状态A,其压强为2.0× 105Pa,体积为2.0×10-3m3,沿直线AB p1.0X10P) 变化到状态B后,压强变为10×105Pa, 体积变为3.0×10-3m3,求此过程中气体 所作的功 分析理想气体作功的表达式为 w =(V)dV.功的数值就等于卫-V图 联.0x103m 4 中过程曲线下所对应的面积。 解 SABD=(BC+AD)x CD 图6-5 故 W=150】

6一6气杠内贮有2,0ol的空气,温度为27℃,若雌持压强不变,而使空 气的体积影胀到原体积的3倍,求空气影胀时所作的功, 分折本周是零限影张过8,气体作功w=货V=(V-V,),其中 压强力可通过态方程求得. 解根据物态方程V1=RT1,气缸内气体的压强卫二RT/V1,则作 功为 W=(V2-Vi)=nRT(V2-Vi)/V =2RT1=9.97×103J

6- 7-定量的空气,吸收了1.71×103J的热量,并保持在1.0×105Pa下 膨胀,体积从1.0×10:2m3增加判1.5×0~之m,问空气对外作了多少功?它 的内能改变了多少? 分析由于气体作等压影胀,气体作功可直接由W=(V2~V1)求得.取 该空气为系统,根据热力学第一定律Q=△E+W可确定它的内能变化.在计算 过程中要注意热量、功、内能的正负取值 解该空气等压影张,对外作功为 W=(V2-V1)=5.0×102Jj 其内能的改变为 △E=Q-W=1.21×103J

6-81.0d的空气从热源吸收了热量2.66×10J,其内能增加了4.18× 10J,在这过程中气体作了多少功?是它对外界作功,还是外界对它作功? 解·由热力学第一定律得气体所作的功为 W=Q-△E=-1.52×105J 负号表示外界对气体作功

6-90.1kg的水蒸气自120℃加热升温至140℃.问:(1)在等体过程 中;(2)在等压过程中,各吸收了多少热量? 分析由量热学知热量的计算公式为Q=nCm△T.按热力学第一定律,在 等排过程中,Qv=△E=nCv,m△T;在等压过程中,Q,=dV+△E= nC,mAT.Cp,m、Cv,m可查表得到. 解(1)在等体过程中吸收的热量为 Qy=AE=Cvm(T2-T)=3.1×103J (2)在等压过程中吸收的热量为 Q,=pdV+△E=,(T-T)=4.0×0J

6-10一压强为1.0×105Pa,体积为1.0×10-3m3的氧气自0℃加热到 100℃.问:(1)当压强不变时,需要多少热量?当体积不变时,需要多少热量? (2)在等压或等体过程中各作了多少功? 分析(1)求Q和Qv的方法与题6-9相同.(2)求过程的作功通常有两 个途径.①利用公式W=}p(V)V;②利用热力学第一定律去求解.在本题 中,热量Q已求出,而内能变化可由4E=nCv,m(T2一T)得到.从而可求得 功. 解根据题给初态条件得氧气的物质的量为 n=程=:VlRT, =4.41×10-2mol 查表知氧气的定压摩尔热容Cp,m=29.44J·md1·K-1,定体摩尔热容 Cw,m=21.12J小molK-. (1)求QpQv 等压过程氧气(系统)吸热 Qo =]pdv+AE=nCp.m(T2-T1) =129.8j 等体过程氧气(系统)吸热 Qy AE=nCv.m(T2-T1)=93.1 J (2)按分析中的两种方法求作功值 ①利用公式W=(V)dV求解.在等压过程中,dW=pdV=RdT, 见得 w,fdw. 而在等体过程中,因气体的体积不变,故作功为 Wy=p(v)dv=0 ②利用热力学第一定律Q=△E+W求解.氧气的内能变化为 △E=Cv,m(Tz-T)=93.1J 由于在(1)中已求出Q,与Qv,则由热力学第一定律可得在等压、等体过程 中所作的功分别为 Wp=Qp-△E=36.7J Ww=Qy-△E=0