
"3-37如图3-37所示,质量分别为m1=10.0kg和m2=6.0kg的两 小球A和B,用质量可略去不计的刚性细杆连接,开始时它们静止在Oxy平面 上,在图示的外力F1=(8.0N)i和F2=(6.0N)j的作用下运动.试求:(1)它 们质心的坐标与时间的函数关系;(2)系统总动量与时间的函数关系, 分析两质点被刚性杆连接构成一整体,其 质心坐标可按质心位矢式求出.虽然两力分别作 用在杆端不同质点上,但对整体而言,可应用质 心运动定律和运动学规律来求解。 3 m 解(1)选如图3-37所示坐标,则t=0 B 时,系统质心的坐标为 0 4m m2 xc0=m1+m2x20=1.5m 图3-37 6w=m1+m23i0=1.9m 1 对小球与杆整体应用质心运动定律,得 R==(+m网)0 (1) R,=2=(m1+m)0 (2) 根据初始条件t=0时,v=0,分别对式(1)式(2)积分可得质心速度的分量与 时间的函数关系式,有 F1 Fde(mdv.v. (3) F2 Pd=g(m1+m2)dw,西=m子m (4) 根据初始条件t=0时,x=x00y=y00,对式(3)、式(4)再一次积分可得质心坐 标与时间的函数关系式,有 ()d c=o+2m1十m72=1.5m+(0.25m·62)2 F dede 国 0二%+2m1tm22=1.9m+(0.19m·s2)2 F2 (2)利用动量定理并考虑到系统的初始状态为静止,可得系统总动量与时 间的函数关系 p=△p=(f1+F2)dt=(8.0kgm·s2)i+(6.0kg·m·s2) 0

4-1一汽车发动机曲轴的转速在12s内由1.2×103r"min1均匀的增加 到2.7×103rmin1.(1)求曲轴转动的角加速度;(2)在此时间内,曲轴转了多 少转? 分析这是刚体的运动学问题,刚体定轴转动的运动学规律与质点的运动 学规律有类似的关系,本题为匀变速转动. 解(1)由于角速度ω=2πn(n为单位时间内的转数),根据角加速度的定 义。=船,在匀变速转动中角如速度为 a=w,0=2πn-0=13.1radg2 (2)发动机曲轴转过的角度为 9=a02+2ar2=2:=t(n+0)t 2 在12s内曲轴转过的图数为 N=是=2”9:=390圈 2

4-2某种电动机启动后转速随时间变化的关系为仙=wo(1-eF),式中 0=9.0s1,x=2.0s.求:(1)t=6.0s时的转速;(2)角加速度随时间变化的规 律;(3)启动后6.0s内转过的圈数. 分析与质点运动学相似,刚体定轴转动的运动学问题也可分为两类:(1) 由转动的运动方程,通过求导得到角速度、角加速度:(2)在确定的初始条件下, 由角速度、角加速度通过积分得到转动的运动方程.本题由仙=ω(t)出发,分别 通过求导和积分得到电动机的角加速度和6.0s内转过的圈数. 解(1)根据题意中转速随时间的变化关系,将t=6.0s代人,即得 w=w0(1-et)=0.95w0=8、6s (2)角加速度随时间变化的规律为 a=da =wet =4.5es2 (3)t=6.0s时转过的角度为 d(ds3.rad 则t=6.0s时电动机转过的圈数 N=8/2r=5.87圈 g=ot+分au2=02=n+aw北 2

4-3如图4一3所示,一通风机的转动部分以初角速度0绕其轴转动, 空气的阻力矩与角速度成正比,比例系数C为一常量.若转动部分对其轴的转 动惯量为J,问:(1)经过多少时间后其转动角速度减少为初角速度的一半?(2) 在此时间内共转过多少转? 分析由于空气的阻力矩与角速度成正比,由转动 定律可知,在变力矩作用下,通风机叶片的转动是变角加 速转动,因此,在讨论转动的运动学关系时,必须从角加 速度和角速度的定义出发,通过积分的方法去解 解(1)通风机叶片所受的阻力矩为M=-C,由 转动定律M=Ja,可得叶片的角加速度为 (1) 图4-3 根据初始条件对式(1)积分,有 由于C和J均为常量,得 wwe月 (2) 当角速度由w0→)0时,转动所需的时间为 t=六ln2 (2)根据初始条件对式(2)积分,有 doweFds 即 0=完 在时间t内所转过的圈数为 N是=器

4-4一燃气轮机在试车时,燃气作用在涡轮上的力矩为2.03×103N·m 涡轮的转动惯量为25.0kgm2.当轮的转速由2.80×103r"min1增大到1.12 ×104rmin1时,所经历的时间t为多少? 分析由于作用在飞轮上的力矩是恒力矩,因此,根据转动定律可知,飞轮 的角加速度是一恒量;又由匀变速转动中角加速度与时间的关系,可解出飞轮所 经历的时间该题还可应用角动量定理直接求解 解1在匀变速转动中,角加速度α= 心二0,由转动定律M=Ja,可得飞 轮所经历的时间 t=M=(a-n0)=10.8s M 解2飞轮在恒外力矩作用下,根据角动量定理,有 ['Mdt=J(o-00) 则 t= 2(n-n0)=10.8s

4一5用落体观察法测定飞轮的转动惯蟹,是将半径为R的飞轮支承在O 点上,然后在绕过飞轮的绳子的一端挂一质量为m的重物,令重物以初速度为 零下落,带动飞轮转动(图4一5).记下重物下落的距离和时间,就可算出飞轮的 转动惯量.试写出它的计算式.(假设轴承间无摩擦) 分析在运动过程中,飞轮和重物的运动形 式是不同的.飞轮作定轴转动,而重物是作落体 运动,它们之间有着内在的联系.由于绳子不可 伸长,并且质量可以忽略.这样,飞轮的转动惯 量,就可根据转动定律和牛顿定律联合来确定, 其中重物的加速度,可通过它下落时的匀加速运 动规律来确定 该题也可用功能关系来处理.将飞轮、重物 和地球视为系统,绳子张力作用于飞轮、重物的 图4-5 功之和为零,系统的机械能守恒.利用匀加速运 动的路程、速度和加速度关系,以及线速度和角速度的关系,代人机械能守恒方 星中即可解得. 解1设绳子的拉力为F,对飞轮而言,根据转动定律,有 FTR Ja (1) 而对重物而言,由牛顿定律,有 mg -FT=ma (2) 由于绳子不可伸长,因此,有 a Ra (3) 重物作匀加速下落,则有 h=Tar (4) 由上述各式可解得飞轮的转动惯量为 J=mR2器 -1 解2根据系统的机械能守恒定律,有 -m8gh+m2+号a2=0 (1) 而线速度和角速度的关系为 =Ro (2) 义根据重物作匀加速运动时,有 =at (3) v2=2ah (4) 由上述各式可得 J=mR(器- 若轴承处存在摩擦,上述测量转动惯量的方法仍可采用.这时,只需通过用 两个不同质量的重物做两次测量即可消除摩擦力矩带来的影响

4-6一飞轮由一直径为30cm,厚度为2.0cm的圆盘和两个直径为 10cm,长为8.0cn的共轴圆柱体组成,设飞轮的密度为7.8×103kg"m3,求飞 轮对轴的转动惯量. 分析根据转动惯量的可叠加性,飞轮对轴 的转动惯量可视为圆盘与两圆柱体对同轴的转 动惯量之和;而匀质圆盘、圆柱体对轴的转动惯 量的计算可查书中公式,或根据转动惯量的定 义,用简单的积分计算得到 解根据转动惯量的叠加性,由匀质圆盘、 图4-6 圆柱体对轴的转动惯量公式可得 J=1+五=2×分m(+m(月 =6ro(ad1+3a)=0.136kgm
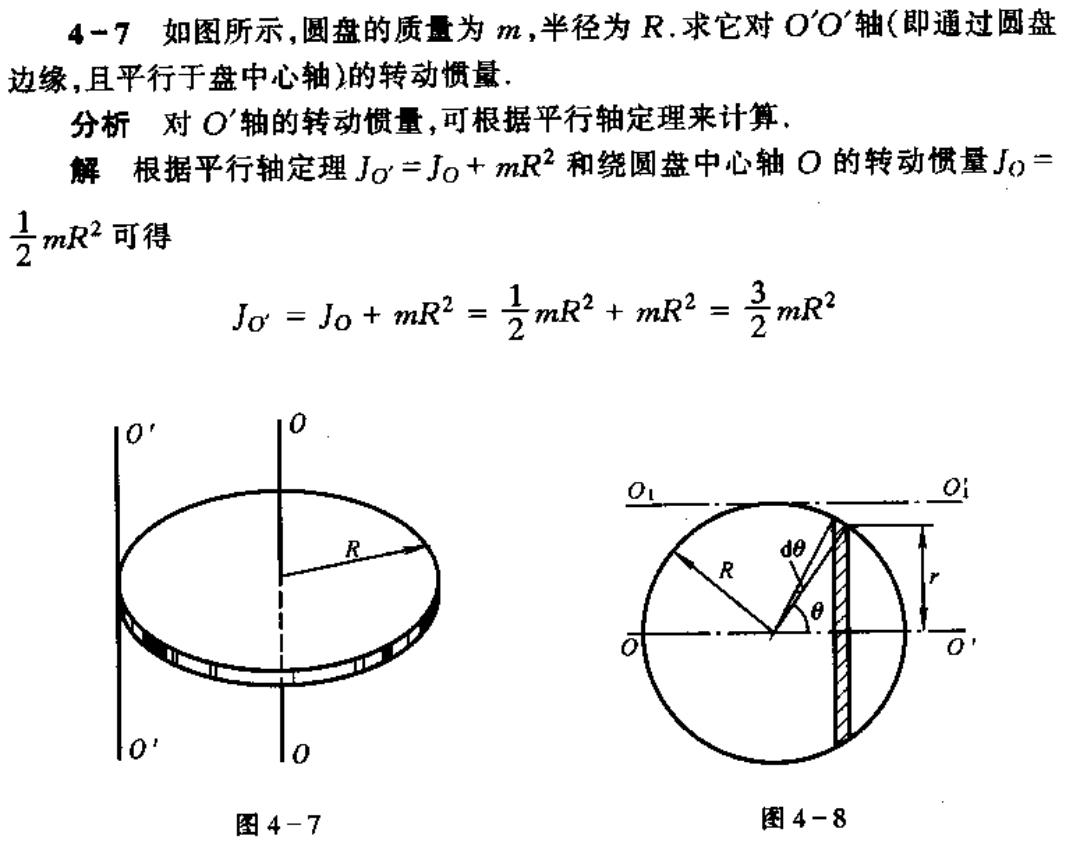
4一7如图所示,圆盘的质量为m,半径为R.求它对OO轴(即通过圆盘 边缘,且平行于盘中心轴的转动惯量. 分析对O轴的转动惯量,可根据平行轴定理来计算, 解根据平行轴定理Jo=J0+mR2和绕圆盘中心轴O的转动惯量Jo= 名mR2可得 Jo Jo+mR2 -mki+m2m 0 图4-7 图4-8

4~8试证明质量为m,半径为R的均匀球体,以直径为转轴的转动惯量 为号mR2,如以和球体相切的线为轴,其转动惯墨又为多少? 分析匀质球体以直径为转轴的转动惯量可视为一系列垂直于转轴的圆盘 组成,这样,在已知圆盘绕其中心轴的转动惯量的基础上,根据转动惯量的叠加 性,采用积分的方法,即可求出球体的转动惯量. 证如图4-8所示,图中阴影部分的小圆盘对O0轴的转动惯量为 d =rdm =(R2-2)p(R2-)dz 式中p=没为匀质球体的密度.则球体以其直径00'为转轴的转动惯量为 J-j小U-2o(R2-2ar=号mR 又由平行轴定理可得球绕O1O轴的转动惯量为 了=J+mR2=子mR2

4一9质量面密度为。的均匀矩形板,试证其对与板面垂直的,通过几何 中心的轴线的转动惯量为员b(2+62).其中1为矩形板的长,b为它的宽。 分析根据转动惯量定义,可直接采用面积 分的方法对匀质矩形板进行计算. 证取如图4-9所示坐标,在板上取一质元 m dm=adxdy,它对与板面垂直的,通过几何中心 b 的轴线的转动惯量为 dI =(z2+y2)adxdy 整个矩形板对该轴的转动惯量为 图4一9 2lb(12+b2)