
17-1在双缝于涉实验中,两缝间距为0.30mm,用单色光垂直照射双 缝,在离缝1.20m的屏上测得中央明纹一侧第5条暗纹与另一侧第5条暗纹间 的距离为22.78mm.问所用光的波长为多少,是什么颜色的光? 分析在双缝干涉中,屏上暗纹位置由x=告(2+1)受决定:所谓第5条 暗纹是指对应=4的那一级暗纹.由于条纹对称,该暗纹到中央明纹中心的距 离x=22,7mm,那么由暗纹公式即可求得波长入. 2 此外,因双缝干涉是等间距的,故也可用条纹间距公式△x=入求入射光 波长.应注意两个第5条暗纹之间所包含的相邻条纹间隔数为9(不是10,为什 么?),故△x=2.78mm. 9 解1屏上暗纹的位登x=号(2k+1)受,把质=4,x=228×103m以 2 及d、d'值代入,可得λ=632.8nm,为红光. 解2屏上相邻暗纹(或明纹)间距△虹-号,把△x=2,78×103n,以及 9 d、d'值代入,可得λ=632.8nm
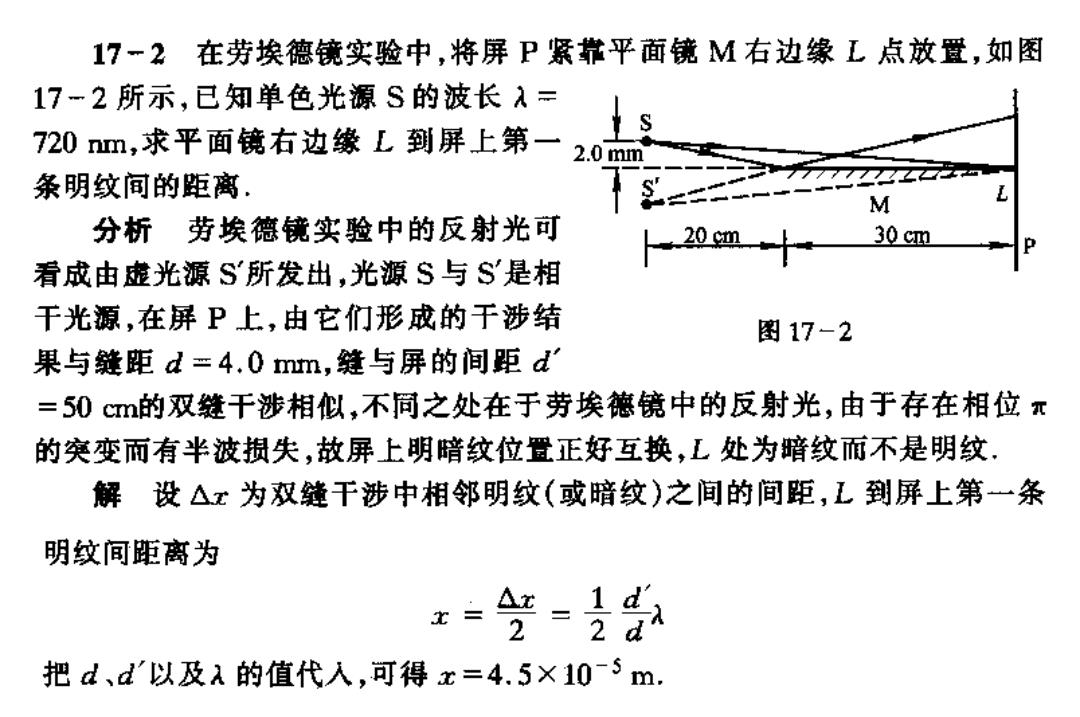
17-2在劳埃德镜实验中,将屏P紧靠平面镜M右边缘L点放置,如图 17-2所示,已知单色光源S的波长入= 720nm,求平面镜右边缘L到屏上第一20 条明纹间的距离。 M 分析劳埃德镜实验中的反射光可 20m 30 cm 看成由虚光源S所发出,光源S与S是相 干光源,在屏P上,由它们形成的干涉结 图17-2 果与缝距d=4.0mm,缝与屏的间距d' =50cm的双缝干涉相似,不同之处在于劳埃德镜中的反射光,由于存在相位π 的突变而有半波损失,故屏上明暗纹位置正好互换,L处为暗纹而不是明纹. 解设△x为双缝干涉中相邻明纹(或暗纹)之间的间距,L到屏上第一条 明纹间距离为 x=-是 把d、d'以及a的值代入,可得x=4.5×10-5m
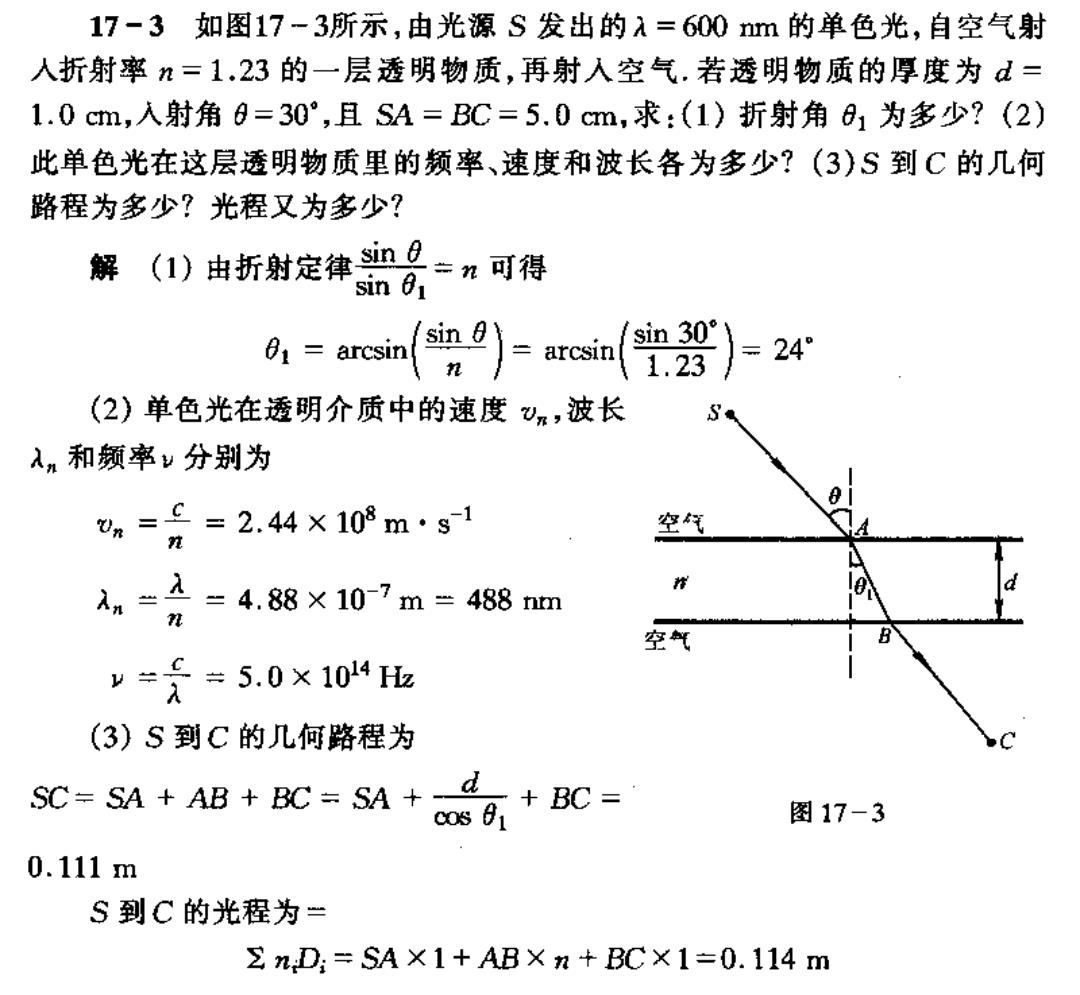
17-3如图17-3所示,由光源S发出的入=600m的单色光,自空气射 人折射率n=1.23的一层透明物质,再射入空气.若透明物质的厚度为d= 1.0cm,入射角0=30°,且SA=BC=5.0cm,求:(1)折射角81为多少?(2) 此单色光在这层透明物质里的频率、速度和波长各为多少?(3)S到C的几何 路程为多少?光程又为多少? 解()由折射定律需昌=可得 ,-arcsinsin9)-arcein(s39)=24 n 1.23 (2)单色光在透明介质中的速度Vm,波长 S 入和频率v分别为 A n=£=2.44×108m·g1 空气 d 入n=2=4.88×10-7m=488m 2 空气 y==5.0×104业 (3)S到C的几何路程为 c0s 0 BC= SC=SA+AB+BC=SA+d。 图17-3 0.111m S到C的光程为= ΣnD:=SA×1+AB×n+BC×1=0.114m

17-4一双缝装置的-…个缝被折射率为1.40的薄玻璃片所遮盖,另一个缝 被折射率为1.70的薄玻璃片所遮盖.在玻璃片插入以后,屏上原来中央极大的 所在点,现变为第五级明纹.假定λ=480m,且两玻璃片厚度均为d,求d值. 分析本题是干涉现象在工程测量中的一个具体应用,它可以用来测量透 明介质薄片的徽小厚度或折射率,在不加介质片之前,两相干光均在空气中传 播,它们到达屏上任一点P的光程差由其几何路程差决定,对于点O,光程差△ =0,故点O处为中央明纹,其余条纹相对点O对称分布.而在插人介质片后, 虽然两相干光在两介质薄片中的几何路程相同,但光程却不同,对于点O,△≠ 0,故点O不再是中央明纹,整个条纹发生平移.可以说,干涉条纹空间分布的变 化完全取决于光程差的变化.因此,对于屏上某点P(明纹或暗纹位置),只要计 算出插人介质片前后光程差的变化,即可知道其干涉条纹的变化情况, 插人介质前的光程差△1=r1-r2=k1入(对应k1级明纹),插入介质后的光 程差42=[(n1-1)d+r1】-[(n2-1)d+r2]=k2a(对应k2级明纹). 光程差的变化量为 △2-△1兰(n2-n1)d=(k2-k1)λ 式中(k2一1)可以理解为移过点P的条纹数(本题为5).因此,对于这类问题, 求解光程差的变化量是解题的关键 解由上述分析可知,两介质片插人前后,对于原中央明纹所在点O,有 △2-41=(n2-n1)d=5λ 将有关数据代入可得 52=8.0m d=2-

17-5如图所示,用白光垂直照射厚度d=400nm的薄膜,若薄膜的折射 图17:4 图17-5 率2=1.40,且n1>n2>n3,问反射光中哪种波长的可见光得到了加强? 分析薄膜干涉中,两相干光之间光程差一般为A=2d√z-nisin2i+ (0或号当光垂直照射时,光程差4=2n2d+(0或号),式中第一项为两相干 光因传播路径不同而引起的光程差,第二项为相位跃变(即半被损失)所带来的 附加光程差.当两相干光均有或均无半波损失时(n1>2>n3或n1 2”3),会引起附加光程差为分,对于薄膜干涉以及后面所述 的劈尖和牛顿环干涉,都必须根据1、2、m3三者之间的关系,认真分析半波损 失对光程差有无影响,而不能随意套用教材中的现成公式.在本题中,由于1> n2>n3,两相干光在薄膜上、下两个表面均无半波损失,故光程差△=2n2d. 解根据以上分析,且由干涉加强条件,有△=2m2d=从,当=2时,A=2d/ k=560m(黄光),该波长在可见光范围内;当k为其他值时,波长均在可见光范围 之外.由于仅有入=560m的光在反射中加强,故此时薄膜从正面看呈黄色

17-6上题中,若薄膜厚度d=350nm,且n22<n3,故反射光的光程差△1=2n2d +今;对于透射光来说,半波损失对透射光的光程差无影响,此时,透射光的光程 差△2=2n2d.由干涉加强或减弱条件即可解得结果, 解(1)反射光的光程差△1=2n2d+),令△1=k入,在可见光范围内讨论 时发现只有一个夷值满足要求,即当=2时,λ2=653.3m的红光在反射中加 强,此时薄膜从正面看呈红色 (2)透射光的光程差42=2m2d,令△2=(2k+1)今,在可见光范围内讨论 时发现当=2时,入2=653.3m的红光在透射中消失。 讨论对于同一薄膜来说,由于41与△2之间相差今,而相邻干涉最强与 最弱之间的光程差也相差分,放反射光与透射光的相干情况正好互补,即入= 653.3m的红光在反射中加强,则在透射中一定相消,这也正好符合能量守恒 这一基本定律

17-7在折射率n3=1.52的照相机镜头表面涂有一层折射率n2=1.38 的MgF2增透膜,若此膜仪适用于被长A=550nm的光,则此膜的最小厚度为多 少? 分析在薄膜干涉中,膜的材料及厚度都将对两反射光(或两透射光)的光 程差产生影响,从而可使某些波长的光在反射(或透射)中得到加强或减弱,这种 选择性使薄膜干涉在工程技术上有很多应用,本题所述的增透膜,就是希望波长 入=550nm的光在透射中得到加强,从而得到所希望的照相效果(因感光底片对 此波长附近的光最为敏感).具体求解时应注意在>0的前提下,取最小的 允许值. 解1因于涉的互补性,波长为550m的光在透射中得到加强,则在反射中一 定减弱,两反射光的光程差42=2m2d,由干涉相消条件42=(2k+1)今,得 a=(2k+1)2 取k=0,则dmin=99.3m 解2由于空气的折射率n1=1,且有n1<n2<n3,则对透射光而言,两相 干光的光程差△1=2md+分,由干涉加强条件△1=从,得 取k=1,则膜的最小厚度dmin=99.3nm

17-8图中S和S2是由同一电源激发的两个点状、同相、相距4.0m的电 磁波源,且发射功率相等,波长为1.0m.若一检波 y/m 器沿Ox方向由S向右移动,问发现几个讯号最 强点?这些点距S多远? 分析本题应首先求出两相干电磁波在x轴4.0m 上任一点的波程差的表达式8(x),满足8(x)= 入的位置处将出现干涉极大,检波器移动到此处 时接收到的讯号最强. 图17-8 解两相干电磁波源S和S2到Ox轴上任一点x处的波程差以及干涉极 大条件为 8=√(4.0m)2+x2-x=k 当k取0,1,2,3,4时,分别得x0→∞,x1=7.5m,x2=3.0m,x3=1.17m, x4=0,即在这些位置,检波器出现干涉极大.由于电磁波在空气中传播时存在 能量损耗,因而,当x0→∞处的干涉极大点实际已不存在,因此,x轴上讯号最 强点共有4个

7-9利用空气劈尖测细丝直径.如图17-9所示,已知λ=589.3nm,L =2.888×10~2m,测得30条条纹的总宽度为4.295×10-3m,求细丝直径d. 分析在应用劈尖干涉公式d=时,应注 意相邻条纹的间距b是N条条纹的宽度△x除以(N -1). 解由分析知,相邻条纹间距6二产1,则细丝 图17-9 直径 d= 22=2NL=5.75×105m 2n26 2n2△x

17-10如图所示,将符合标准的轴承钢珠a、b和待测钢珠c一起放在两 块平板玻璃之间,若垂直人射光的波长入=580m,问钢珠c的直径比标准小多 少?如果距离d不同,对检测结果有何影响? 分析很显然,如钢珠c与标准件a、b相同,则呈现厚度相同的薄膜干涉: 如钢珠与标准件不同,则为劈尖干涉.后者有等厚干涉条纹出现,a与c之间的 条纹分布如图17-10(6)所示.由于相邻条纹的厚度差△d=2元2而空气的折射 率n2≈1,则两锅珠之间的直径差△x=N),式中N为a与c之间的条纹间隔 数目(注:条纹数目较多时,也可用条纹数目作近似计算),由图17一10(a)知N 约为6} 改变钢珠间的距离d,将钢珠c移至c'处,如图17-10(c)所示,a与c'之间 条纹数并未改变,但由于相邻条纹间距变小,从而影响观测 a(b) (a) (b) (c) 图17-10 解钢珠c和a、b的直径不同,则两平板玻璃形成空气劈.由分析得,钢珠c 的直径与标准件直径相差 △x=N受=1.81×106m 当距离d稍微改变时,a、b与c之间条纹数目未变,故不影响检验结果