
1-1已知质点沿x轴作直线运动,其运动方程为x=2m+(6ms2)2- (2ms3)3.求:(1)质点在运动开始后4.0s内位移的大小:(2)质点在该时闻 内所通过的路程. 分析位移和路程是两个完全不同的概念,只有当质点作直线运动且运动 方向不改变时,位移的大小才会与路程相等,质点在t时同内的位移△x的大小 可直楼由运动方程得到:△x=4一x0,而在求路程时,就必须注意到质点在运动 过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据是 =0来确定其运动方向改变的时刻tb,求出0~。和2~t内的位移大小△1 △x2,则t时间内的路程s=【△x|+|Ax2|,见图1-1 解(1)质点在4.0s内位移的大小 △r=x4-0=-32m (2)由 =(12mg2)t-(6ms)2=0 dt 得知质点的换向时刻为 t。=2s(t=0不合愿意) 则 r'm -30 10 △r1=x2-x0=8.0m △x2=x4-x2=-40m 图1-1 所以,质点在40s时间间隔内的路程为 s=|△x11+|△x21=48m
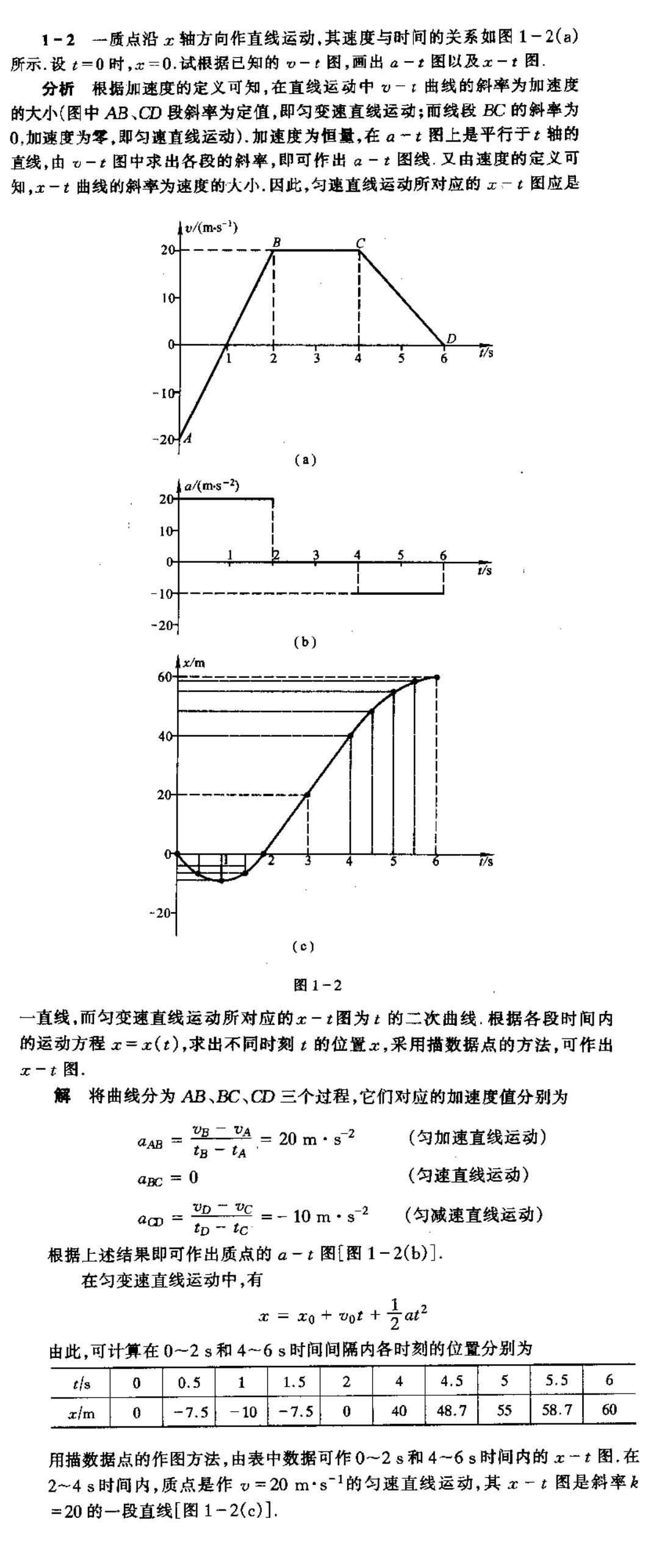
1-2一质点沿x轴方向作直线运动.其速度与时间的关系如图1-2() 所示.设t=0时,士=0,试根据已知的o-:图,画出a一t图以及x一t图 分析根据加速度的定义可知,在直线运动中?一:曲蚁的斜率为加速度 的大小(图中AB、CD段斜率为定值,即匀变速直线运动:而线:C的料率为 0,加球度为零,即匀速直线运动).加速度为恒量,在a一t图上是平行于:轴的 直线,血。一图中求出各段的斜率,即可作出4一:图线.又由速度的定义可 知,x一t曲线的斜率为速度的大小,因此,匀速直线运动所对应的x一:图应是 w(m-s) 20 10 a/(ms-2) -20 (b) 40 20 图1-2 一直线,而匀变速直线运动所对应的x一t图为t的二次曲线.根据各段时间内 的运动方程x■x(t),求出不同时刻的位置x,采用描数据点的方法,可作出 x-t图 解将曲线分为AB、BC、CD三个过程,它们对应的如速度值分别为 a。 贺二A=20m·s2 (匀加速直线运动) Ig tA aRC=0 (匀速直线运动)】 am=2二=-10m·s2 (匀诚速直线运动)】 tp-tc 极据上述结果即可作出质点的a-t图[图1-2(b)]. 在匀变速直线运动中,有 由此,可计算在0一2s和4~6s时间间隔内各时刻的位数分别为 tis 0 0.5 1 1.5 2 4 4,5 5 5.5 6 x/m 0 -7.5 -10 =7,5 0 40 48.7 55 58.7 60 用描数菇点的作图方法,由表中数据可作0一2s和4一6s时间内的x一t图,在 2~4s时间内,质点是作v=20m·s1的匀速直线运动,其x一t图是斜率 =20的一段直线[图1-2(c)]

1-3如图1-3()所示,潮中有一小船.岸上有人用绳跨过定滑轮拉船靠 岸,设滑轮距水面高度为h,滑轮到原船位置的绳长为。.试求:当人以匀速e 拉绳时,船运动的速度为多少? (b) 图1-3 分析首先进定船为研究的对象,它的速度也就是绳端点的移动速度, 绳上各点的移动速度是不相同的:而绳速。是指收绳的速率,是绳上各点沿绳 运动的快慢,也就是绳上各点速度在绳方向的分量,绳速和船速是两个不同的概 念.认为绳上各点的速度相同或将船的速度大小'视为绳速。的分量均是错误 的 定量描述船的运动状态和规律,必须建立确定的坐标系(所选坐标系可以不 相同),写出船在此坐标系中的运动方程,并根据速度和加速度的定义式,即可解 出问题 解1取如图1一3(b)所示的直角坐标系.船的运动方程为 r(:)=x(t)i+(-h)j 船的运动速度为 -部==品--(-)当 dt dt 而收绳的速率。=出,且因,=6-,放 解2取图1-3()所示的极坐标(r,0),则 o'= drdr dt da" dt ,是船的径向速度一品,是船的機向滤度,面出是收绳的速率由于船速。 dr. 与径向速度之间夹角为日,所以 -(h cegi--v1- h2 由此可知,收绳的速率只是船速沿绳方向的分景
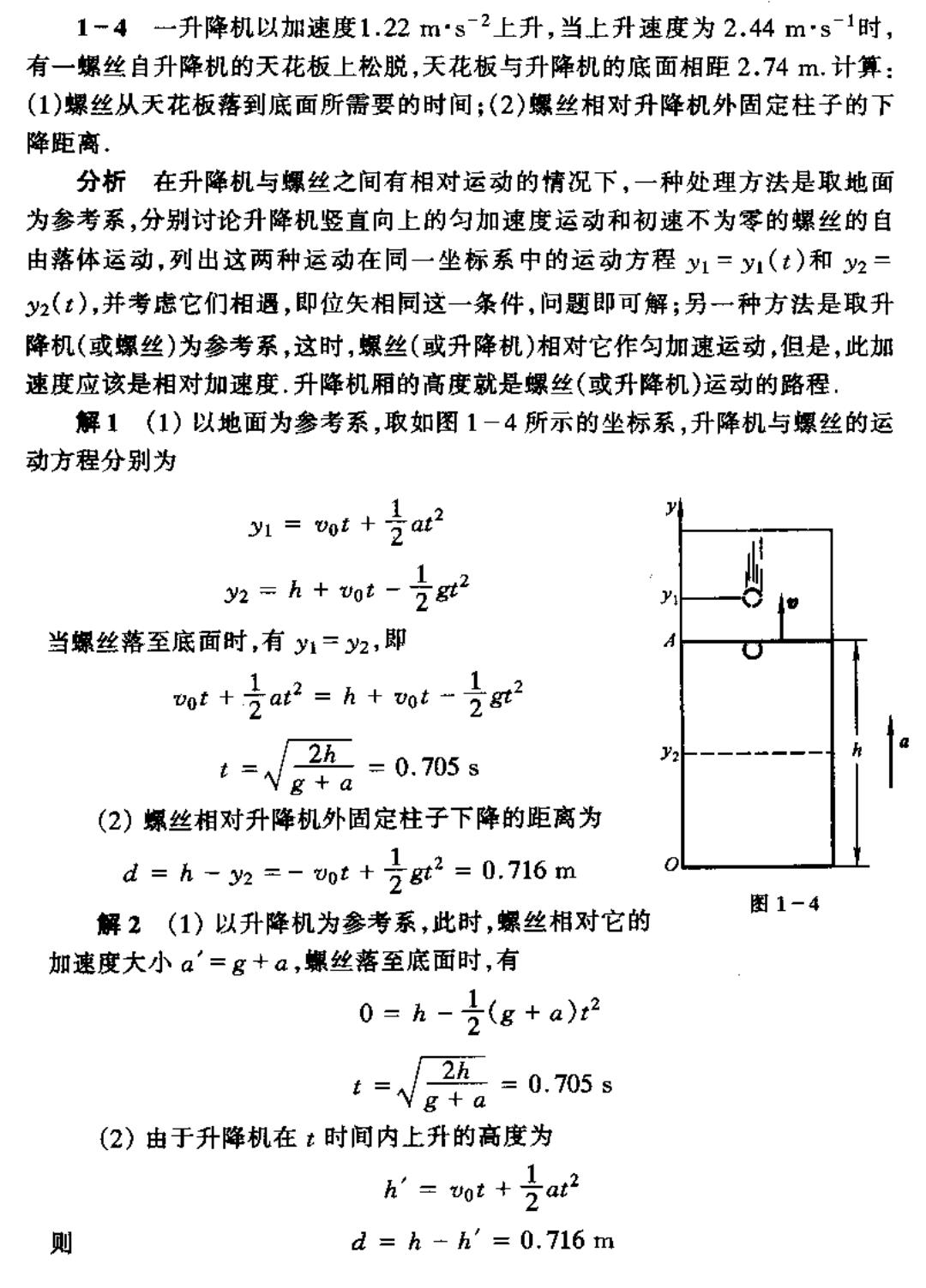
1-4一升降机以加速度1.22m·s2上升,当上升速度为2.44ms1时 有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距2.74m.计算: (1)螺丝从天花板落到底面所需要的时间;(2)螺丝相对升降机外固定柱子的下 降距离. 分析在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面 为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自 由落体运动,列出这两种运动在同一坐标系中的运动方程y=y(t)和2 y2(:),并考虑它们相遇,即位矢相同这一条件,问题即可解;另一种方法是取升 降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加 速度应该是相对加速度,升降机厢的高度就是螺丝(或升降机)运动的路程, 解1(1)以地面为参考系,取如图1一4所示的坐标系,升降机与螺丝的运 动方程分别为 y1 vot +at2 次=h+0t-7 当螺丝落至底面时,有y1=火,即 ● vot+at=h+votgt 4-√g。=0.75s (2)螺丝相对升降机外固定柱子下降的距离为 d=h-2=-ott号g2=0.716m 解2(1)以升降机为参考系,此时,螺丝相对它的 图1-4 加速度大小a'=g+a,螺丝落至底面时,有 0=h-(g+a)r2 -=0.705s (2)由于升降机在t时间内上升的高度为 h'=0t+7at2 d=h-h'=0.716m
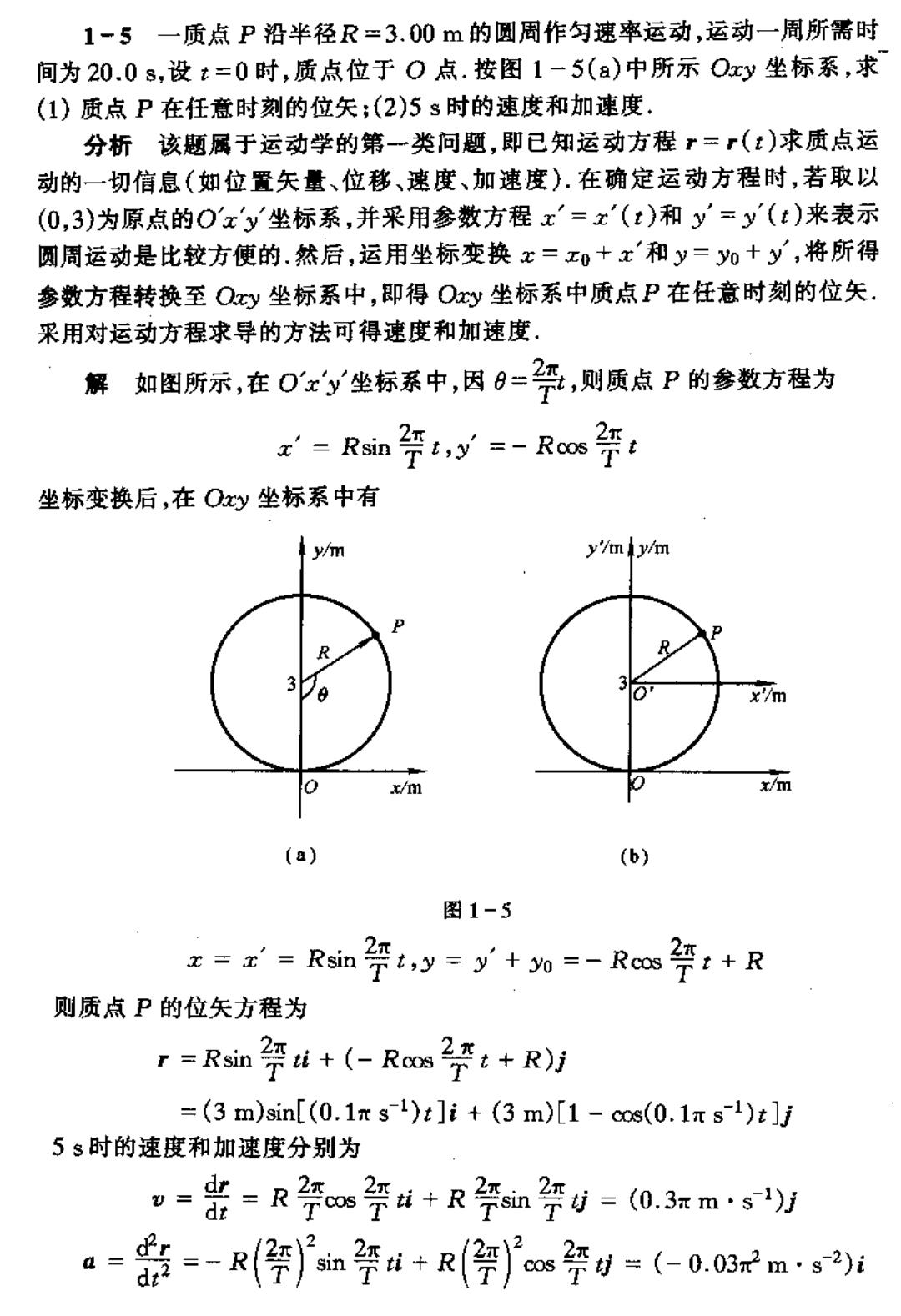
1-5一质点P沿半径R=3.00m的圆周作匀速率运动,运动一周所需时 间为20.0s,设t=0时,质点位于0点.按图1-5(a)中所示Oxy坐标系,求 (1)质点P在任意时刻的位矢;(2)5s时的速度和加速度. 分析该题属于运动学的第一类问题,即已知运动方程r=r(t)求质点运 动的一切信息(如位置矢量、位移、速度、加速度).在确定运动方程时,若取以 (O,3)为原点的Ox'y坐标系,并采用参数方程x'=x'(t)和y=y(t)来表示 圆周运动是比较方便的.然后,运用坐标变换x=z0+x和y=y0+y,将所得 参数方程转换至Qy坐标系中,即得Oy坐标系中质点P在任意时刻的位矢 采用对运动方程求导的方法可得速度和加速度, 解如图所示,在0'xy坐标系中,因9=经,则质点P的参数方程为 x=Rsin9t,y=-Ros年t 坐标变换后,在Oxy坐标系中有 A y/m y/m y/m (a) 6) 图1-5 x=x'=Rsin祭t,y=y+o=-Rcos祭t+R 则质点P的位矢方程为 r=Rsim年i+(-Rs2t+R)j =(3 m)sin[(0.1m s)]i+(3m)[1-cos(0.1 s-1)t]j 5s时的速度和加速度分别为 o=贵-R亭s亭+R祭m停=0.3xmg万 a-能=-R(停m祭i+R停)cas—=(←0.03m·s2i dt2

1-6一质点自原点开始沿抛物线y=bx2运动,它在Ox轴上的分速度 为一恒量,其值为z=4.0ms1,b=0.5m1.求质点位于x=2.0m处的速 度和加速度 分析抛物线y=x2是质点的轨迹方程,它是参数方程 z=I(t).y=y(t) 合成的结果.由于:是已知的,可得x方向.上的运动方程x=x(t)及加速度分 量az,由x=x(t)和轨迹方程y=f(x),求得运动方程在y方向上的分量式 y=y(t)及其加速度分量ay,再由速度和加速度的分量可得其矢量表达式. 解因:=4.0ms1为一常量,故a:=0.当=0时,x=0,由u-积 分可得 x=U主 (1) 又由质点的抛物线方程,有 =bx2=b()2 (2) 由y方向的运动方程可得该方向的速度和加速度分量分别为 y==22 (3) (4) 当质点位于x=2.0m时,由上述各式可得 口=+j=(4.0m·s1)i+(8.0m·s1j a=a+a=(16ms2

1-7质点在Oy平面内运动,其运动方程为r=(2.00m·s1)i+ [19.0m-(2.00ms2)2]j.求:(1)质点的轨迹方程;(2)在t1=1.00s到2 =2.00s时间内的平均速度;(3)t1=1.00s时的速度及切向和法向加速度. 分析根据运动方程可直接写出其分量式x=x(t)和y=y(t),从中消去 参数t,即得质点的轨迹方程.平均速度是反映质点在一段时间内位置的变化 率,即元=△r△t,它与时间间獬△t的大小有关,当△t→0时,平均速度的极限 即桑时速度。=切向和法向加速度是指在自然坐标下的分矢量a,和a,前 者只反映质点在切线方向速度大小的变化率,即。:=,后者只反映质点速 度方向的变化,它可由总加速度a和a:得到, 解(1)由参数方程 x=(2.00m·s1)t,y=19.0m-(2.00m·s2)t2 消去t得质点的轨迹方程: y=19.0m-(0.50m1)x2 (2)在t1=1.00s到t2=2.00s时间内的平均速度 万=签-名名-2mmg-(6o0mgy (3)质点在任意时刻的速度和加速度分别为 ()=4+y1=0+0j=(2.0m…g1i-4.00m·s2为 a(t)= +=40a 则t1=1,00s时的速度 o(t)l=1。=(2.00m·s1)i-(4.00m·g1)j 切向和法向加速度分别为 al=,= 80=是62+k,=3.58mg2)e aa=√a2-aen=(1.79m·s2)en

1-8质点的运动方程为 x=(-10m·s1)t+(30m·s2)t2 y=(15m·s1)t-(20m·82)2 试求:(1)初速度的大小和方向;(2)加速度的大小和方向. 分析由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成 算出速度和加速度的大小和方向。 解(1)速度的分量式为 =能=-10mg1+(60ms2 =8¥=15ms1-(40ms22 当t=0时,℃0z=-10ms1,v0y=15m"s1,则初速度大小为 0=√z+6y=18.0m·s1 设v0与x轴的夹角为a,则 g-路=-》 a=123°411 (2)加速度的分量式为 a==60m·g2,4=0=-40m·g2 则加速度的大小为 a=ya+a3=72.1m·s2 设a与x轴的夹角为日,则 级B-经=一号 B=-3341'(或32619)

1-9一质点具有恒定加速度a=(6ms2)i+(4ms2)j,在t=0时, 其速度为零,位置失量r0=(10m)i.求:(1)在任意时刻的速度和位置矢量;(2) 质点在Ozy平面上的轨迹方程,并画出轨迹的示意图. 分析该题属于质点运动学的第二类问题,即已知速度或加速度的表达式 v=(t)或a=a(t),求运动方程r=r(t),它是第一类问题的逆过程,是一段 时间内运动量的积累.处理这类问题,必须在给定的初始条件下,采用积分的方 法来解决。 解由加速度定义式,根据初始条件to=0时0=0,积分可得 0 =0[(6m·s2i+(4mg2)j1d 0=(6m·s2)t+(4m·s2) 又由-出及初始条件1=0时,0=(10mi,积分可得 dr=dt=J0[(6m…s2)i+(4m·s2)]d r=[10m+(3m·s2)t2]i+[(2m·s2)t2]j 由上述结果可得质点运动方程的分量式,即 m x=10m+(3m·s2)t2 y=(2m·s2)t2 消去参数:,可得运动的轨迹方程 3y=2x-20m 3y=2x-20m 这是一个直线方程直线斜率k==g。 20L a=3341'.轨迹如图1-9所示. 图1-9

1-10飞机以100ms1的速度沿水平直线飞行,在离地面高为100m时 驾驶员要把物品空投到前方某一地面目标处.问:(1)此时目标在飞机下方前多 进?(2)投放物品时,驾驶员看目标的视线和水平线成何角度?(3)物品投出 200.s后,它的法向加速度和切向加速度各为多少? 分析物品空投后作平抛运动.忽略空气阻力的条件下,由运动独立性原理 知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动.到达 地面目标时,两方向上运动时间是相同的.因此,分别列出其运动方程,运用时间 相等的条件,即可求解 此外,平抛物体在运动过程中只存在竖直向下的重力加速度,为求特定时刻 t时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间 的夹角。或B.由图1一10可知,在特定时刻t,物体的切向加速度和水平线之间 的夹角a,可由此时刻的两速度分盘vz、℃,求出,这样,也就可将重力加速度g 的切向和法向分量求得 解(1)取如图所示的坐标,物品下 落时在水平和竖直方向的运动方程分别 为 x-wy-i8 飞机水平飞行速度v=100m's1,飞机 离地面的高度y=100m,由上述两式可为mnn7n77 得目标在飞机正下方前的距离 2y=452m 图1-10 (2)视线和水平线的夹角为 0=aretg¥=12.S° (3)在任意时刻物品的速度与水平轴的夹角为 a=arcg经=arctg 取自然坐标,物品在抛出2s时,重力加速度的切向分量与法向分量分别为 a4=gsin a=gsinarctg)=1.88m·s2 a=gosa=8os(acg号)=9.62m·s2