习思 题1业1:妇图所示。两根长直导线互相平行地收置,导线内电流大小相等,均为!■10A,方向 相同,如图所示。来图中从,N两点的短球强度B的大小和方向(图中m-0020m, 年N 81 a 恩1心2:已知地球业极地场延够强度B的大小为60x103T。如设塑此地磁场是由她球赤道上 一圆电流所激发的(如图所示),此电流有多大?流向如阿? 题10.3:如图所示,载流导线在平面内分布,电流为山它在点O的腿多强度为多少: a 题1Q如图所示,率轻为R的木球上接有密集的细导线,线围平面腹此平行,几以单层线圈 夏盖住率个球面。设线图的总更数为,通过线图的电黄为了,求球心O处的磁感强度, 题1业5:实验中常用所谓的变姆霜兹线圈在局 区域内获得一近似均匀的型场,其装置简围 如图所示,一对完全相同、被此平行的线圈, 它门的半径均为是。通过的电流均为上,且两 线圈中电麓的流向相同。试证,当两线圈中心 之间的距离d等于线圆的米径R时,在两线圈 中心连线的中点附近区域,避场可看成是均匀 磁场,〔提示:如以两线图中心为坐标原点O, a 两线圈中心连线为x轴,则中点财近的城场可 看成是均匀延场的条件为 d 0)
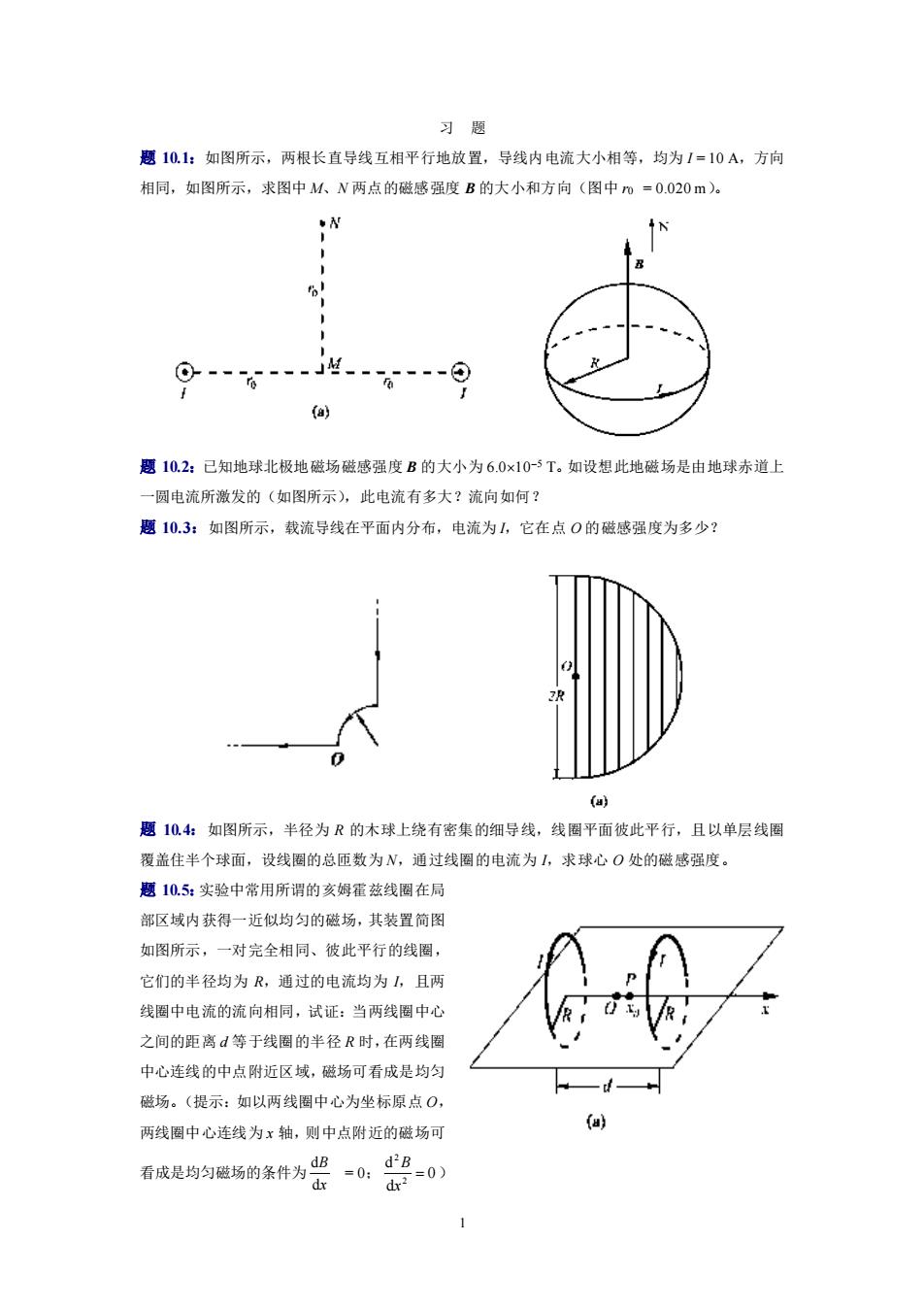
1 习 题 题 10.1:如图所示,两根长直导线互相平行地放置,导线内电流大小相等,均为 I = 10 A,方向 相同,如图所示,求图中 M、N 两点的磁感强度 B 的大小和方向(图中 r0 = 0.020 m)。 题 10.2:已知地球北极地磁场磁感强度 B 的大小为 6.010−5 T。如设想此地磁场是由地球赤道上 一圆电流所激发的(如图所示),此电流有多大?流向如何? 题 10.3:如图所示,载流导线在平面内分布,电流为 I,它在点 O 的磁感强度为多少? 题 10.4:如图所示,半径为 R 的木球上绕有密集的细导线,线圈平面彼此平行,且以单层线圈 覆盖住半个球面,设线圈的总匝数为 N,通过线圈的电流为 I,求球心 O 处的磁感强度。 题 10.5:实验中常用所谓的亥姆霍兹线圈在局 部区域内获得一近似均匀的磁场,其装置简图 如图所示,一对完全相同、彼此平行的线圈, 它们的半径均为 R,通过的电流均为 I,且两 线圈中电流的流向相同,试证:当两线圈中心 之间的距离 d 等于线圈的半径 R 时,在两线圈 中心连线的中点附近区域,磁场可看成是均匀 磁场。(提示:如以两线圈中心为坐标原点 O, 两线圈中心连线为 x 轴,则中点附近的磁场可 看成是均匀磁场的条件为 x B d d = 0; 0 d d 2 2 = x B )
想10,6,如图所示,载流长直导找的电流为人。试求通过距形面积的磁通量。 a 题1山7:如图所示,在够强瘦为B的均匀磁场中,有一半轻为R的半球面,B与半球面轴线 的夹角为@,求通过该半球面的磁通量。 题1L8已知10m世视铜线允许通过50A电流而不金使导线过热,电流在导规横戴面上均匀 分布。浅:(1)导线内,外题感强度的分布:(2)导找表面的磁够强度。 题1外有一同轴电境。其尺寸如图所示。两导棒中的电流均为,但电流的流向图反,导体的 磁性可不考虑。试计算以下各处的@感强度:(1)<R:(2)RR:(3)R4:《4)PR: 面出B一r图线: 倒 题11如图所示,N匝线圈均匀密绕在截面为长方彩的中空骨架上,求通入电流I后,环内 外磁场的分布。 题1血11:设有两无限大平行载流平面,它们的电流密度均为小电流流向相反,如图所示,求: (1)两载流平面之间的磁多强度:(2》两面之外空间的磁感强度。 U- 恩112:测定离子颜量的质谱仪如图所示,离子源S产生顺最为m。电背为g的离子。离子的 初速很小,可看作是静止的,经电势差如速后离子速入融感强度为B的均幻融场,并沿一率 2
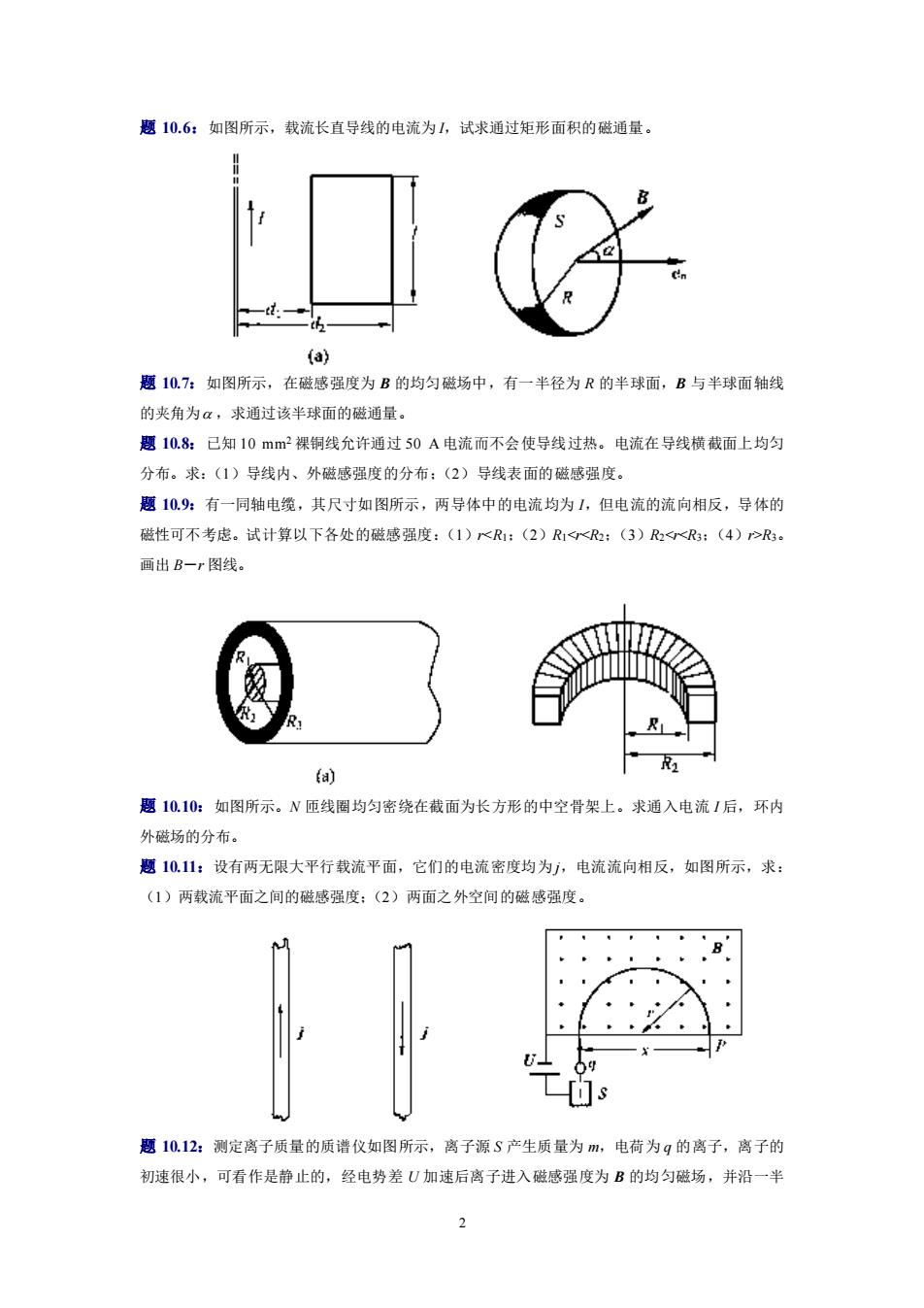
2 题 10.6:如图所示,载流长直导线的电流为 I,试求通过矩形面积的磁通量。 题 10.7:如图所示,在磁感强度为 B 的均匀磁场中,有一半径为 R 的半球面,B 与半球面轴线 的夹角为 ,求通过该半球面的磁通量。 题 10.8:已知 10 mm2 裸铜线允许通过 50 A 电流而不会使导线过热。电流在导线横截面上均匀 分布。求:(1)导线内、外磁感强度的分布;(2)导线表面的磁感强度。 题 10.9:有一同轴电缆,其尺寸如图所示,两导体中的电流均为 I,但电流的流向相反,导体的 磁性可不考虑。试计算以下各处的磁感强度:(1)rR3。 画出 B-r 图线。 题 10.10:如图所示。N 匝线圈均匀密绕在截面为长方形的中空骨架上。求通入电流 I 后,环内 外磁场的分布。 题 10.11:设有两无限大平行载流平面,它们的电流密度均为 j,电流流向相反,如图所示,求: (1)两载流平面之间的磁感强度;(2)两面之外空间的磁感强度。 题 10.12:测定离子质量的质谱仪如图所示,离子源 S 产生质量为 m,电荷为 q 的离子,离子的 初速很小,可看作是静止的,经电势差 U 加速后离子进入磁感强度为 B 的均匀磁场,并沿一半
周形轨道到达离入口处距离为x的感光底片上,试证明连高子的质量为 8'4x 题113己知地面上空某处地做场的碱感登度B=04×104T,方向向北。若学宙射线中有一 速率r■50x10m:s的顺子。垂直地通过该处。如图所示,求:(1洛伦弦力的方向:2)洛伦 燕力的大小,并与该质子受到的万有引力相比较: B 恩1川14:在一个显檬管的电子束中,电子有12×10V的能量,这个显檬管安放的位置桂电子 水平地由南向北运动。地球磁场的垂直分量B.=55×0$T,并且方向向下。求:电子束偏 转方向:2)电子束在是锋管内通过20cm到达解由时光点的偏转间距: 题1015如图所示。设有一质量为m的电子射 入壁感强瘦为B的均匀磁场中,当它位于点时, 具有与慰场方向成:角的速度,它都螺餐线运动 一周到达点N,试证从,W两点间的距离为 MV2mroosa eB 题1业16:利用密耳元件可以测量硫场的磁感强度。设一需耳元件用金属材料制成,其厚度为015 mm。载流子数密度为1.0×104m一。将霍耳元件放入待测磁场中,测得霍耳电压为42V,电 流为10mA。求此时待测磁场的磁感强度。 题10.17:试证明霍耳电场强度与稳恒电场强度之比 Eu /Ee -BImep 这里为材料电阻省,n为靓液子的数密度。 恩1山18:载流子浓度是率导体材料的重要参数,工艺 上通过拉制三价或五价排柔厚子的沫度,来控制P型 或型华导体的载流子浓度,利用霍耳效应可以测量 规流子的末度和类型,如图所示一块半导体材料样品, 均匀磁场垂直于样品表面,样品中通过的电流为,我 测得霍耳电压为州,证明样品载黄子浓度为 B
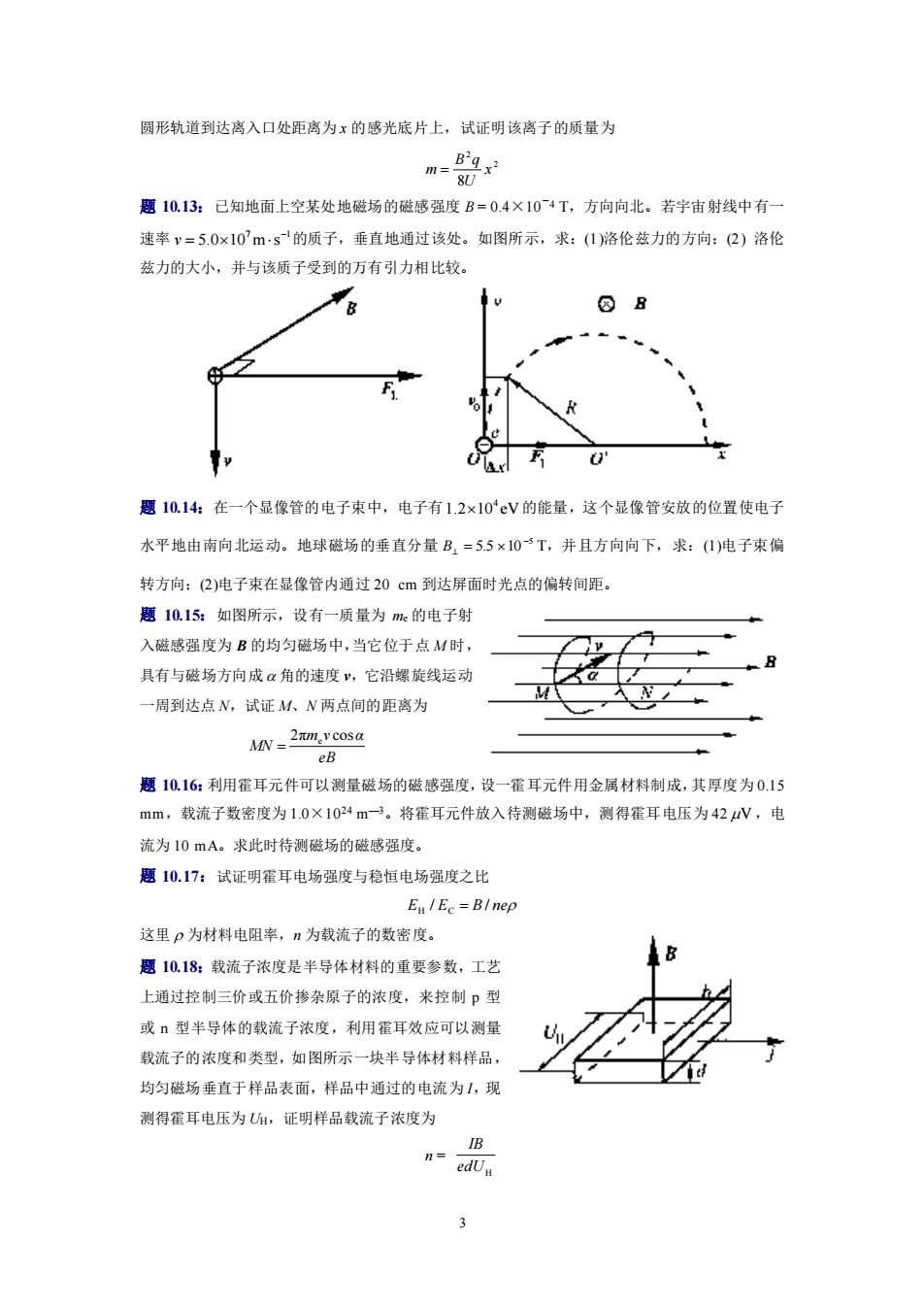
3 圆形轨道到达离入口处距离为 x 的感光底片上,试证明该离子的质量为 2 2 8 x U B q m = 题 10.13:已知地面上空某处地磁场的磁感强度 B = 0.4×10-4 T,方向向北。若宇宙射线中有一 速率 7 1 5.0 10 m s − v = 的质子,垂直地通过该处。如图所示,求:(1)洛伦兹力的方向;(2) 洛伦 兹力的大小,并与该质子受到的万有引力相比较。 题 10.14:在一个显像管的电子束中,电子有 1.2 10 eV4 的能量,这个显像管安放的位置使电子 水平地由南向北运动。地球磁场的垂直分量 5 5.5 10 − B⊥ = T,并且方向向下,求:(1)电子束偏 转方向;(2)电子束在显像管内通过 20 cm 到达屏面时光点的偏转间距。 题 10.15:如图所示,设有一质量为 me 的电子射 入磁感强度为 B 的均匀磁场中,当它位于点 M 时, 具有与磁场方向成 角的速度 v,它沿螺旋线运动 一周到达点 N,试证 M、N 两点间的距离为 eB m v α MN 2π cos e = 题 10.16:利用霍耳元件可以测量磁场的磁感强度,设一霍耳元件用金属材料制成,其厚度为 0.15 mm,载流子数密度为 1.0×1024 m—3。将霍耳元件放入待测磁场中,测得霍耳电压为 42 V ,电 流为 10 mA。求此时待测磁场的磁感强度。 题 10.17:试证明霍耳电场强度与稳恒电场强度之比 EH / EC = B / ne 这里 为材料电阻率,n 为载流子的数密度。 题 10.18:载流子浓度是半导体材料的重要参数,工艺 上通过控制三价或五价掺杂原子的浓度,来控制 p 型 或 n 型半导体的载流子浓度,利用霍耳效应可以测量 载流子的浓度和类型,如图所示一块半导体材料样品, 均匀磁场垂直于样品表面,样品中通过的电流为 I,现 测得霍耳电压为 UH,证明样品载流子浓度为 n = H edU IB
题11身一通有电流为/的导线,弯成如图所示的形状,放在 碱感强度为B的均陆场中,B的方向垂直纸面向里,求此导线 受到的安绪力为多少? 题1020:一直流变电站将电医为300kV的直流电,通过两条蓝 面不计的平行输电线输向远方,已如两输电导线可单位长度的电 容为3,0×10F-m,若号线阿的静电力与安幅力正好抵清, 求:(1)通过输电战的电流:(2)输送的功率。 a 题1《:将一电流均匀分布的无限大载流平面成入磁够强度为 B的均匀壁场中,电流方向与难场垂直,敢入后,平面两侧础场 的磁感强度分别为B1和B:《图),求该线流平面上单位面积所受 的磁场力的大小和方向。 题1L22:在直径为10©m的铜棒上,切割下一个同盘,设想这 个圆盘的厚度只有一个原子线度那么大,这样在圆盘上约有 62×104个铜原予,每个铜原予有27个电子,每个电子的自旋 磁矩为从,-93×10Am2。我们假设所有电子的白能磁矩方向 都相同。且平行于啊棒的轴线,求:(1)圆盘的磁矩:(2》如这程矩是由圆盘上的电流产生的, 那么圆盘边峰上需要有多大的电流。 题1L23:通有电流山=50A的无限长直导战,放在如图所示的形线面的柏线上,线圈中的电 流左=20A,找圈高A73,乘作用在规图上的力: 题124如图所示,在一通有电流/的长直导线附近,有一半轻为R,质量为用的细小线圈, 睡小线国可绕通过其中心与直导线平行的轴转诗,直导线与闻小线圈中心相距为d,设d>R, 通过小线圈的电流为”。若开始时线圈是静止的,它的正法线矢量#,的方白与纸面法线,的方 向成队角。间线图平面转至与解存面重叠时,角速度的值为多大? 愿1025如图所承。电率为P的金属圆环,其内外半径分别为风和风,厚度为d。圆环成 入壁感强瘦为口的均匀壁场中,B的方向与圆环平面垂直,将圆环内外边缘分别接在如图所示
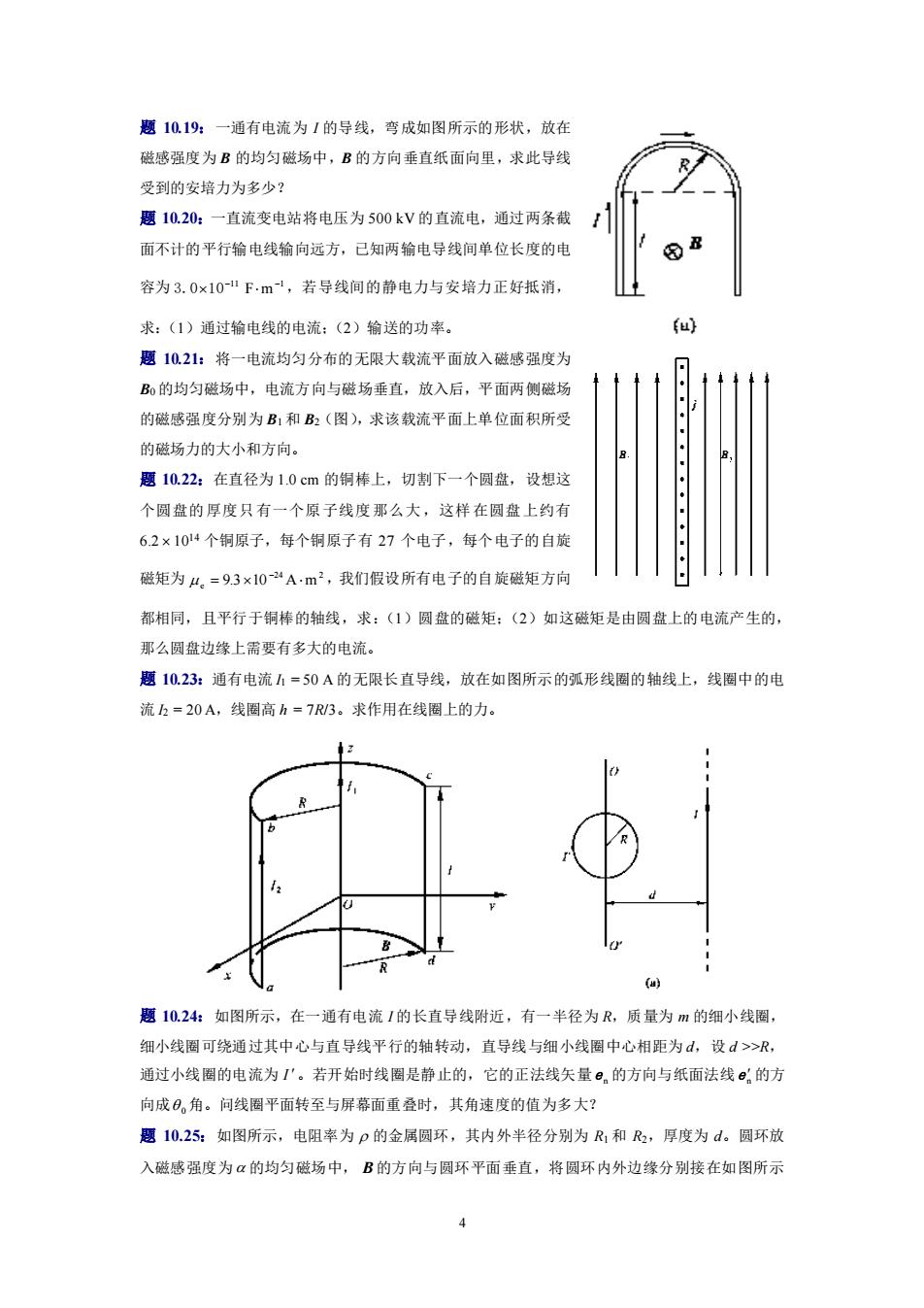
4 题 10.19:一通有电流为 I 的导线,弯成如图所示的形状,放在 磁感强度为 B 的均匀磁场中,B 的方向垂直纸面向里,求此导线 受到的安培力为多少? 题 10.20:一直流变电站将电压为 500 kV 的直流电,通过两条截 面不计的平行输电线输向远方,已知两输电导线间单位长度的电 容为 11 1 3.0 10− − Fm ,若导线间的静电力与安培力正好抵消, 求:(1)通过输电线的电流;(2)输送的功率。 题 10.21:将一电流均匀分布的无限大载流平面放入磁感强度为 B0 的均匀磁场中,电流方向与磁场垂直,放入后,平面两侧磁场 的磁感强度分别为 B1 和 B2(图),求该载流平面上单位面积所受 的磁场力的大小和方向。 题 10.22:在直径为 1.0 cm 的铜棒上,切割下一个圆盘,设想这 个圆盘的厚度只有一个原子线度那么大,这样在圆盘上约有 6.2 1014 个铜原子,每个铜原子有 27 个电子,每个电子的自旋 磁矩为 24 2 e = 9.3 10 Am − ,我们假设所有电子的自旋磁矩方向 都相同,且平行于铜棒的轴线,求:(1)圆盘的磁矩;(2)如这磁矩是由圆盘上的电流产生的, 那么圆盘边缘上需要有多大的电流。 题 10.23:通有电流 I1 = 50 A 的无限长直导线,放在如图所示的弧形线圈的轴线上,线圈中的电 流 I2 = 20 A,线圈高 h = 7R/3。求作用在线圈上的力。 题 10.24:如图所示,在一通有电流 I 的长直导线附近,有一半径为 R,质量为 m 的细小线圈, 细小线圈可绕通过其中心与直导线平行的轴转动,直导线与细小线圈中心相距为 d,设 d >>R, 通过小线圈的电流为 I 。若开始时线圈是静止的,它的正法线矢量 e n 的方向与纸面法线 e n 的方 向成 0 角。问线圈平面转至与屏幕面重叠时,其角速度的值为多大? 题 10.25:如图所示,电阻率为 的金属圆环,其内外半径分别为 R1 和 R2,厚度为 d。圆环放 入磁感强度为 的均匀磁场中, B 的方向与圆环平面垂直,将圆环内外边缘分别接在如图所示

的电动势为x的电源两极。圆环可绕通过环心乐直环面的轴转动,求圆环所受的磁力矩。 a 题12制如图所承,常径为R的圆片均匀带电,电荷面密度为口,令该到片以角速度。绕通 过其中心且垂直于圆平面的轴旋转。求轴战上距网片中心为¥处的点P的融感强度和旋转圆片 的姬矩。 题10,27:如图所示是一种正在研究中的电磁物道炮的原理图。该装置可用于发射速度高达0 kms的烛弹,超弹置于两条平行轨道之间与轨道相接触。轨道是半径为r的圆性形导体,轨道 间距为d。饱弹沿轨道可以自由滑动。何流电界£、饱弹和轨道构成一团合回路,回路中电流为 1(1》正明作用在炮辣上的赋场力为 F=42 (2)假设/=4300kA,d=20■m,7=67cm,烟弹从静止起经过一段路程L=4.0m知速日 的速度为多大?(设炮弹质量网一100kg) 5
5 的电动势为 的电源两极,圆环可绕通过环心垂直环面的轴转动,求圆环所受的磁力矩。 题 10.26:如图所示,半径为 R 的圆片均匀带电,电荷面密度为 ,令该圆片以角速度 绕通 过其中心且垂直于圆平面的轴旋转。求轴线上距圆片中心为 x 处的点 P 的磁感强度和旋转圆片 的磁矩。 题 10.27:如图所示是一种正在研究中的电磁轨道炮的原理图。该装置可用于发射速度高达 10 km.s-1 的炮弹,炮弹置于两条平行轨道之间与轨道相接触,轨道是半径为 r 的圆柱形导体,轨道 间距为 d。炮弹沿轨道可以自由滑动。恒流电源 、炮弹和轨道构成一闭合回路,回路中电流为 I。(1)证明作用在炮弹上的磁场力为 r μ I d r F + = )ln π ( 2 1 2 0 (2)假设 I = 4 500 kA,d = 120 mm,r = 6.7 cm,炮弹从静止起经过一段路程 L = 4.0 m 加速后 的速度为多大?(设炮弹质量 m = 10.0 kg)
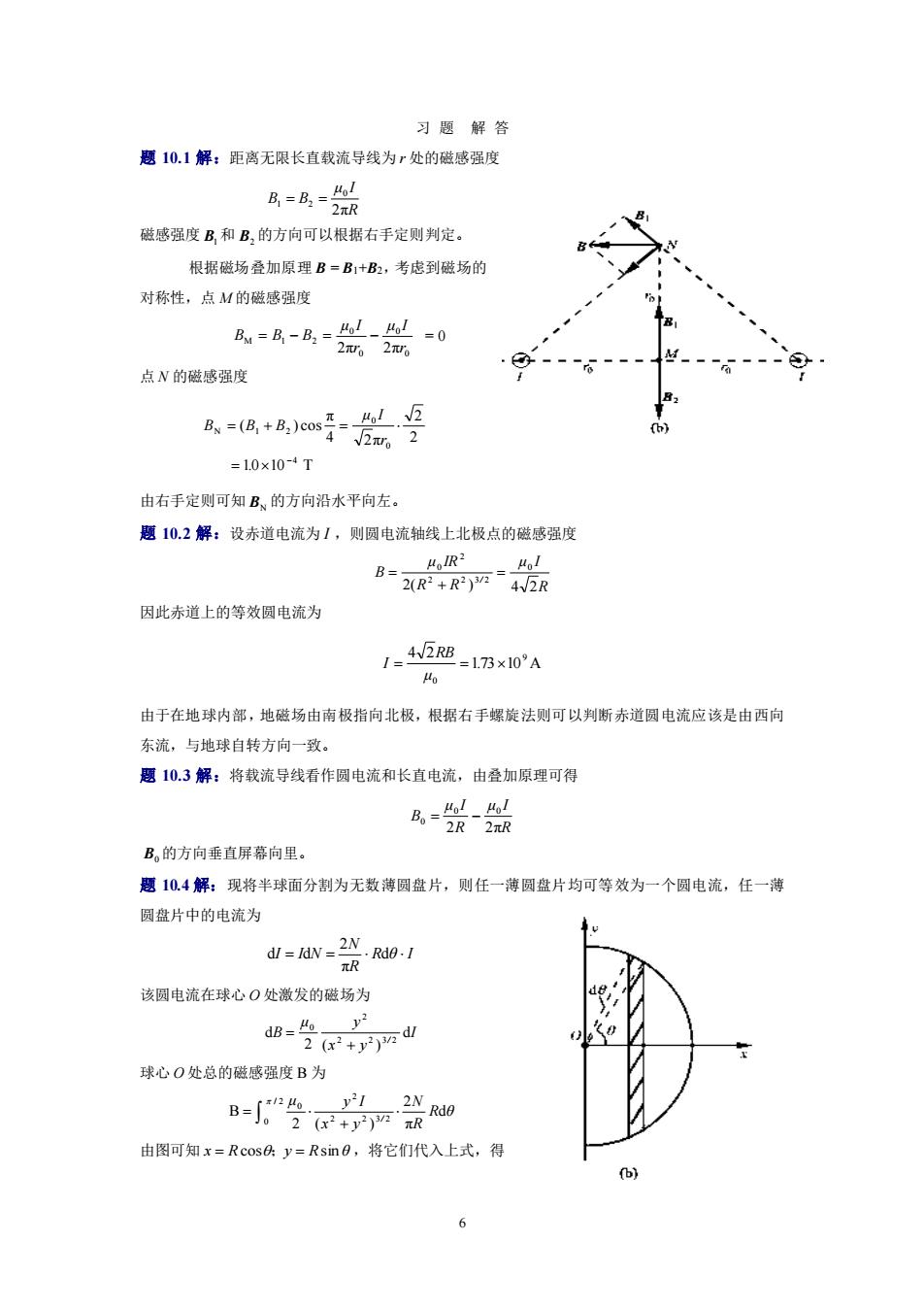
习思解答 思10,1解,距离无限长直规液导线为r处的磁感强度 岛欲 磁感强度®和®,的方向可以根据右手定则判定。 限据磁场叠加原理B■B1+B:。考虑到赋场的 对移性。点AM的磁够星度 B=房-品=兴-是0 2w12w。 点N的磁8强度 R、=(8+B)s是=L园 422 =10×104T 由右于定则可知B的方向沿水平向左。 题10.2解:设赤道电流为1,则网电流轴线上北极点的磁感强度 B= 4R2 2R+R7"42R 因此赤道上的等效网电流为 142 =17B×10°A 由于在地球内部,她磁场由南极指向北极。根据右手螺旋法则可以判断赤道圆电流应该是由西向 东流,与地球白转方向一数。 题103解,将载流导线看作园电流和长直电流,山叠加原理可得 民= 2R 2aR B,的方向垂直屏幕向里。 题1机4解:现将竿球面分制为无数薄圆盘片,刚任一薄圆盆片均可等效为一个圆电流。任一薄 园查片中的电流为 d山=N-2R附0-1 .周电流在球心0处激发的场为 dB。凸 22+d 球心O处总的腿程度B为 -台n议 山图可知言=R©s网y=Rsm8,将它们代入上式,得 时
6 习 题 解 答 题 10.1 解:距离无限长直载流导线为 r 处的磁感强度 R μ I B B 2π 0 1 = 2 = 磁感强度 B1 和 B2 的方向可以根据右手定则判定。 根据磁场叠加原理 B = B1+B2,考虑到磁场的 对称性,点 M 的磁感强度 0 0 0 0 M 1 2 2π 2πr μ I r μ I B = B − B = − = 0 点 N 的磁感强度 10 10 T 2 2 4 2π π ( ) cos 4 0 0 N 1 2 − = = + = . r μ I B B B 由右手定则可知 BN 的方向沿水平向左。 题 10.2 解:设赤道电流为 I ,则圆电流轴线上北极点的磁感强度 R μ I R R μ IR B / 2( ) 4 2 0 2 2 3 2 2 0 = + = 因此赤道上的等效圆电流为 173 10 A 4 2 9 0 = = . μ RB I 由于在地球内部,地磁场由南极指向北极,根据右手螺旋法则可以判断赤道圆电流应该是由西向 东流,与地球自转方向一致。 题 10.3 解:将载流导线看作圆电流和长直电流,由叠加原理可得 R μ I R μ I B 2 2π 0 0 0 = − B0 的方向垂直屏幕向里。 题 10.4 解:现将半球面分割为无数薄圆盘片,则任一薄圆盘片均可等效为一个圆电流,任一薄 圆盘片中的电流为 R θ I R N I = I N = d π 2 d d 该圆电流在球心 O 处激发的磁场为 I x y μ y B / d 2 ( ) d 2 2 3 2 2 0 + = 球心 O 处总的磁感强度 B 为 R θ R N x y μ y I / d π 2 2 ( ) B / 2 0 2 2 3 2 2 0 + = 由图可知 x = Rcos; y = Rsin θ ,将它们代入上式,得
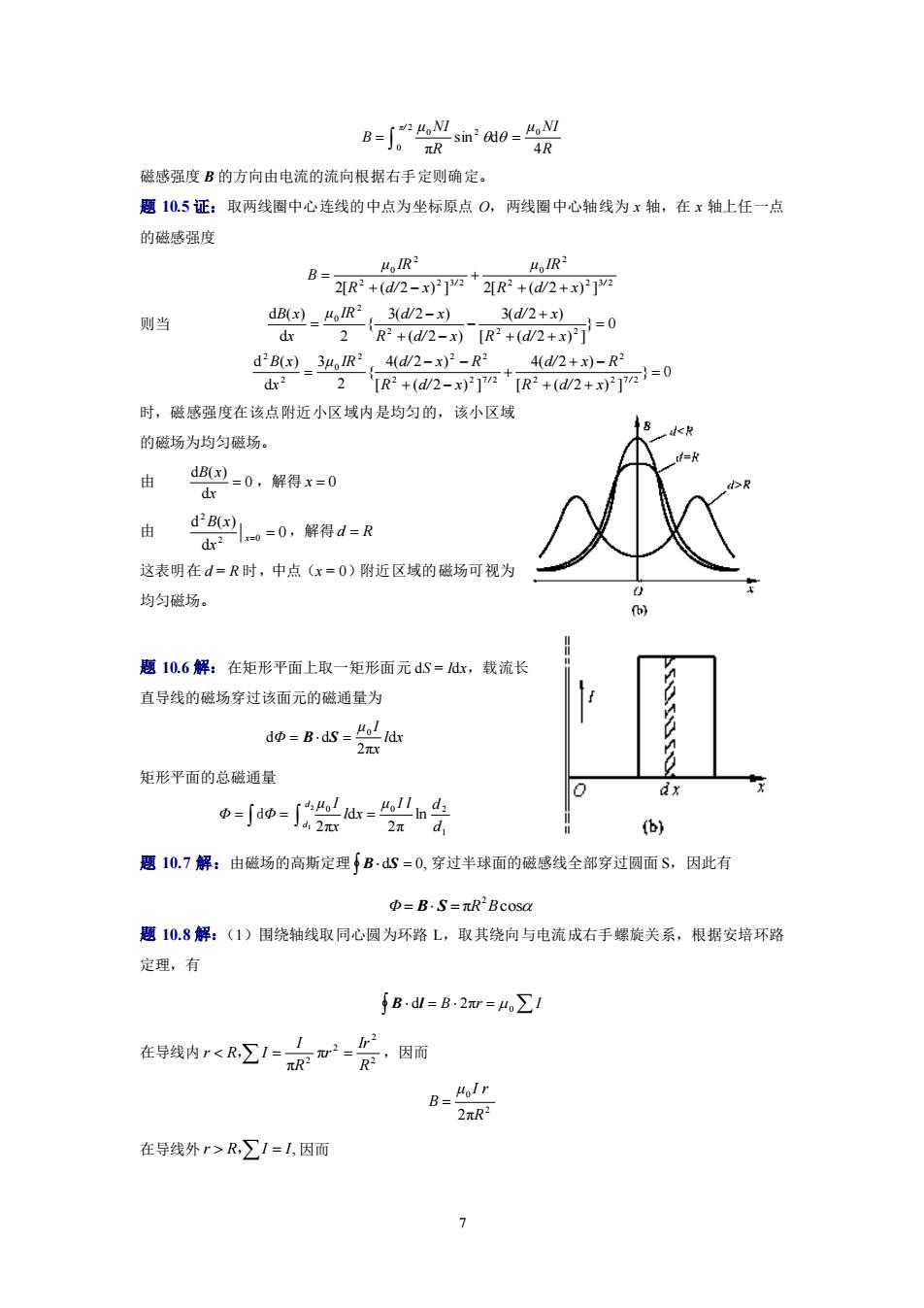
8-0ha0 4R 磁移强度B的方向由电流的速向根据右手定则确定。 思15证:取两线圈中心连线的中点为学标原点0,两线图中心轴线为x轴,在x轴上任一点 的是感保度 B= R M2 2R+d2-产R+d2+x 则当 d过-4R2,3d2-对 =2+2-R+d2+=0 d'B(x)3R 4d2-x°-R34d2+x-R dr 2 顶+2-丽2+d2+对-0 时,磁感强度在该点附近小区域内是均匀的,该小区域 的场为均匀磁场。 d倒-0,解得x-0 d山 由 w=0,解得d=R d所1 这表明在d=R时,中点(x=0》附近区城的磁场可视为 均匀础场。 题1L6解:在矩形平而上取一矩形而元dS=,载流长 直导线的磁场穿过该面元的磁通量为 d帅=Bd5-是a 矩形平面的总磁通量 0 =o=岩=受 2x d (b) 恩10.7解:由磁场的高斯定理「B,心=0.穿注常球面的随然找全部穿过园面S。因此有 =B-S=R'Bcosa 题10.8解:《1》围晓轴线取同心圆为环路L,取其烧向与电藏成右手螺轮关系。服据安培环路 定理,有 手B,d山-B2w-4∑ 在特线内R∑1=1,因面
7 R μ NI R μ NI B π/ 4 sin d π 2 0 2 0 0 = = 磁感强度 B 的方向由电流的流向根据右手定则确定。 题 10.5 证:取两线圈中心连线的中点为坐标原点 O,两线圈中心轴线为 x 轴,在 x 轴上任一点 的磁感强度 2 2 3 2 2 0 2 2 3 2 2 0 2[ ( 2 ) ] 2[ ( 2 ) ] / / R d/ x μ IR R d/ x μ IR B + + + + − = 则当 } 0 [ ( 2 ) ] 3( 2 ) ( 2 ) 3( 2 ) { d 2 d ( ) 2 2 2 2 0 = + + + − + − − = R d/ x d/ x R d/ x μ IR d/ x x B x = 0 + + + − + + − − − = } [ ( 2 ) ] 4( 2 ) [ ( 2 ) ] 4( 2 ) { 2 3 d d ( ) 2 2 7 2 2 2 2 7 2 2 2 2 0 2 2 / / R d/ x d/ x R R d/ x μ IR d/ x R x B x 时,磁感强度在该点附近小区域内是均匀的,该小区域 的磁场为均匀磁场。 由 0 d d ( ) = x B x ,解得 x = 0 由 0 d d ( ) 2 0 2 x= = x B x ,解得 d = R 这表明在 d = R 时,中点(x = 0)附近区域的磁场可视为 均匀磁场。 题 10.6 解:在矩形平面上取一矩形面元 dS = Idx,载流长 直导线的磁场穿过该面元的磁通量为 l x x μ I Φ d 2π d d 0 = B S = 矩形平面的总磁通量 Φ = dΦ = = 2 1 1 0 0 2 ln 2π d 2π d d d μ I l d l x x μ I 题 10.7 解:由磁场的高斯定理 B dS = 0, 穿过半球面的磁感线全部穿过圆面 S,因此有 π cos 2 Φ = B S = R B 题 10.8 解:(1)围绕轴线取同心圆为环路 L,取其绕向与电流成右手螺旋关系,根据安培环路 定理,有 = B r = I d 2π 0 B l 在导线内 = = 2 2 2 2 π π R Ir r R I r R, I ,因而 2 0 2πR μ I r B = 在导线外 r R,I = I, 因而
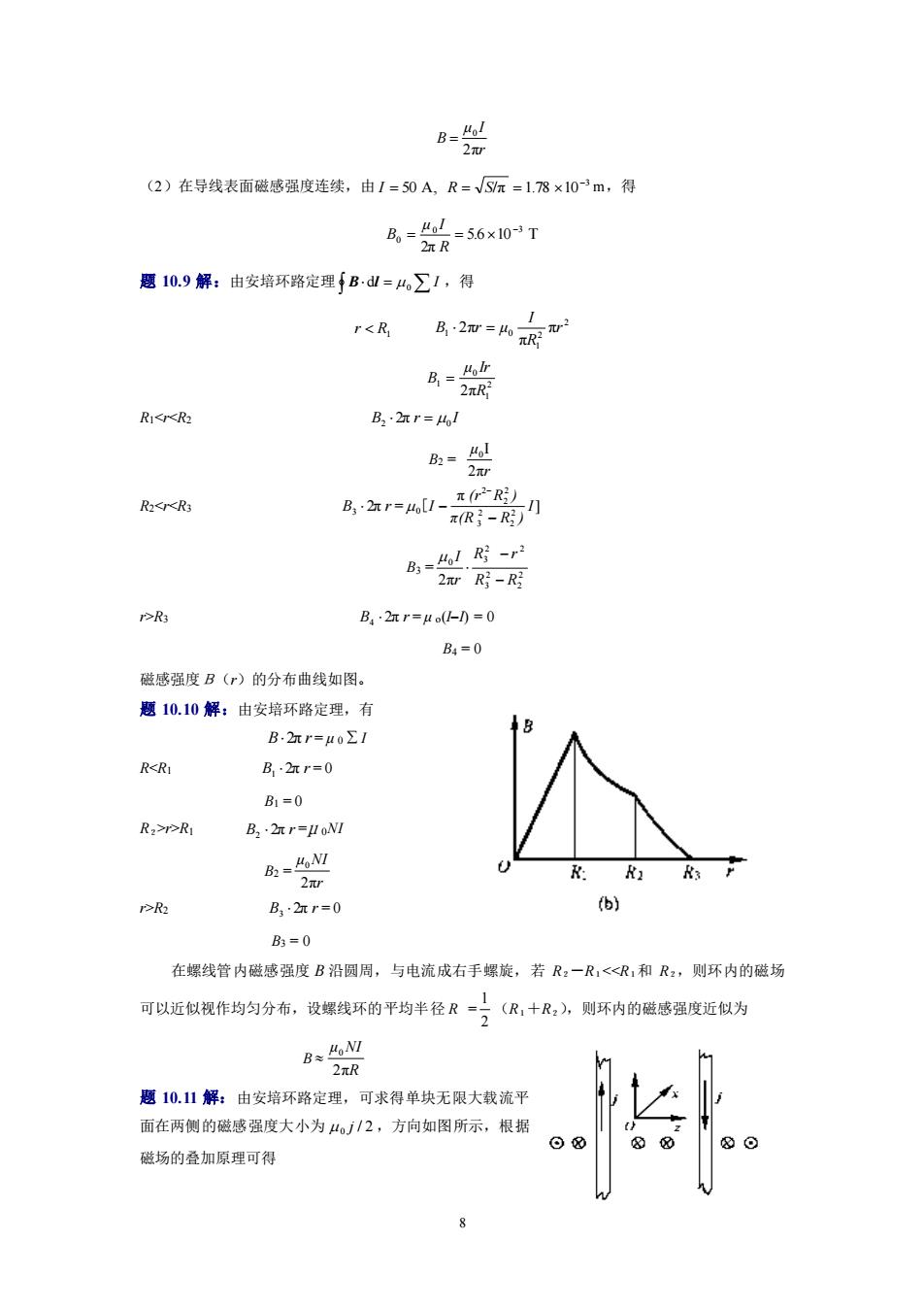
B=4! 2 (2)在导线表面做感强度连续,由1=50A.R=√京=18×10m,得 成==56×10T 红R 恩10,9解:由安婚环路定理手B《=叫∑1,得 r<R B2w=叫 能 RIK B红r-4 品▣ 2 局 岛a-毫 岛鸟-r 2wR-阴 2是 B-r=wd-0=0 B=0 随够强度B(r)的分右由线如图。 题10.10解:由安培环路定理,有 B.点r=HoEI RCRI B·r=0 所-0 R:2R B立r-uW 岛■些7 2ar P的 B,女r=0 6 =0 在螺线管内赋感强度B沿同周,与电流成右千螺能,若R:一R,<R,和R:,测环内的赋场 可以近似视作均匀分布。设螺找环的平均半径及“立 (R,十R:》则环内的磁感强度近似为 Be色M 2元R 10.11解:由安培环路定理,可求得单块无限大载流平 面在两侧的磁感强度大小为2,方门如图所示,限据 磁场的叠加原理可得
8 r μ I B 2π 0 = (2)在导线表面磁感强度连续,由 3 50 A, /π 1.78 10 − I = R = S = m,得 56 10 T 2π 0 3 0 − = = . R μ I B 题 10.9 解:由安培环路定理 = I d 0 B l ,得 R1 r 2 2 1 1 0 π π 2π r R I B r = μ 2 1 0 1 2πR μ Ir B = R1R3 B 2π r 4 = μ o(I−I) = 0 B4 = 0 磁感强度B(r)的分布曲线如图。 题 10.10 解:由安培环路定理,有 B2π r = μ 0 I Rr>R1 B 2π r 2 =μ 0NI B2 = r μ NI 2π 0 r>R2 B 2π r 3 = 0 B3 = 0 在螺线管内磁感强度 B 沿圆周,与电流成右手螺旋,若 R2-R1<<R1和 R2,则环内的磁场 可以近似视作均匀分布,设螺线环的平均半径 R = 2 1 (R1+R2),则环内的磁感强度近似为 B R μ NI 2π 0 题 10.11 解:由安培环路定理,可求得单块无限大载流平 面在两侧的磁感强度大小为 0 j / 2 ,方向如图所示,根据 磁场的叠加原理可得

(1)取里直于煤幕向里为x轴正向,合壁场为 B=以+=所 2 2 (2)两导体载流平面之外。合壁场的确感强度 8-4i-i=0 2 2 题10.12证:由离子源产生的离予在电势差为U的电场中如速。服据对使定理,有 支m产-g0 (1) 离子以速率,速入磁场后,在洛伦独力的作用下作圆属阔动。其动力学方餐为 gr8-wx/2 由上述两式可得m■ 89x2 题10.13解,(1)依限F■gΨ×8可知洛轮兹力F方向为?×B的方向, (2)因,⊥B,质子所受的洛伦兹力 F■gvB=32×10-1sN 在地球表面顺子所受的万有引力 G=两g■164×10-N 因而,有FG■195×I0,即质子所受的洛伦点力远大于重力 题10.14解:(1)如图所示。山洛伦弦力 F-qvxB 可以判断电子束将偏向东侧 (2》在如图所示的坐标中。电子在洛伦燕力作用下,沿圆圆运动,其转道单径R为 R-雪-2正=671m eg eg 由赠知y■20m,并由图中的几何关系可得电子束偏向东侧的距离 4x=R-VR-y2=2.98x10m 甲显示屏上的图像将整体白素平移近3mm,这种平移并不会影响整幅图像的质量 题1儿15正:算入射电子的迪度沿槛场方向和在直燃场方向分解,和w:在磁场方向前进一螺距1N 所蓄的时间 T-A0V-A0V (1) T。0a 在垂直腿场方间的平面内,电子作匀速圆周超动的周用 T2-2m (2) V eB 由式(1)和式(2),可得 9
9 (1)取垂直于屏幕向里为 x 轴正向,合磁场为 B = i i μ ji μ j μ j 0 0 0 2 2 + = (2)两导体载流平面之外,合磁场的磁感强度 B = 0 2 2 0 0 i − i = j j 题 10.12 证:由离子源产生的离子在电势差为 U 的电场中加速,根据动能定理,有 mv = qU 2 2 1 (1) 离子以速率 v 进入磁场后,在洛伦兹力的作用下作圆周运动,其动力学方程为 qvB = m / 2 2 x v 由上述两式可得 2 2 8 x U B q m = 题 10.13 解:(1)依照 FL = qv B 可知洛伦兹力 FL 方向为 v B 的方向, (2)因 v ⊥ B,质子所受的洛伦兹力 FL = qvB = 3.210−16 N 在地球表面质子所受的万有引力 G = mpg = 1.6410−26 N 因而,有 FL/G = 1.95 1010,即质子所受的洛伦兹力远大于重力 题 10.14 解:(1)如图所示,由洛伦兹力 F = qv B 可以判断电子束将偏向东侧 (2)在如图所示的坐标中,电子在洛伦兹力作用下,沿圆周运动,其轨道半径 R 为 R = 6.71 m 2 k = = eB mE eB mv 由题知 y = 20cm,并由图中的几何关系可得电子束偏向东侧的距离 2.98 10 m 2 2 −3 x = R − R − y = 即显示屏上的图像将整体向东平移近 3 mm,这种平移并不会影响整幅图像的质量 题 10.15 证:将入射电子的速度沿磁场方向和垂直磁场方向分解 ⊥ v 和 v//,在磁场方向前进一螺距 MN 所需的时间 T = // vcosα MN v MN = (1) 在垂直磁场方向的平面内,电子作匀速圆周运动的周期 T = v eB 2πR 2πme = ⊥ (2) 由式(1)和式(2),可得

AMY=2mm.vcosa cB 恩10.16解:由霍耳效应中霍耳电压与电莲、磁移强度的关氣,有 8 Uud Und R/四-00T 题10.17证:由欧鲜定律的微分形式知,在导体内稳恒电场滋度为 E.-pJ-pv 由霍耳效应,霍耳电场强度 EI■-P×B 因载流子定向运动方向与磁够强度正交,故E一vB,因面 Eu=TB=r8=8 Ec per mep 恩118证:通电率导体的截流子在洛伦致力的作用下,逐渐积案在相距为b的导体两侧,形成霍耳 电压 CH =Y86 而流经导体横截面S(3■)的电流 I-ibd-nerbd 由此可解有载流子浓度 edUn 题119解:由对称性可知,半到凰所受安培力F的水平分 量相互(消为零。极有 A-可d识-Rsn闭8-2R 两段直线留分所受安培力大小相等,但方向相反,当导体形 状不变时,该两力平衡,因而,整个导线所受安培力 F-28R1 题120解:(1)单位长度导线所受的安痛力和静电力分别 为 角=M。 2ud 左-E-Cy 2ad 山长■0可得 42_CU 2d28d 解得 ==45x10'A EiHa 10
10 eB m v MN 2π e cos = 题 10.16 解:由霍耳效应中霍耳电压与电流、磁感强度的关系,有 B = 010 T H H H nq . I U d R I U d = = 题 10.17 证:由欧姆定律的微分形式知,在导体内稳恒电场强度为 E j nev c = = 由霍耳效应,霍耳电场强度 EH = −v B 因载流子定向运动方向与磁感强度正交,故 EH = vB,因而 ne B nev vB j vB E E = = = C H 题 10.18 证:通电半导体的载流子在洛伦兹力的作用下,逐渐积聚在相距为 b 的导体两侧,形成霍耳 电压 UH = vBb 而流经导体横截面 S(S = bd)的电流 I = jbd = nevbd 由此可解得载流子浓度 n = H edU IB 题 10.19 解:由对称性可知,半圆弧所受安培力 F1 的水平分 量相互抵消为零,故有 F1 = = = π F BIR BIR 0 d 1y sind 2 两段直线部分所受安培力大小相等,但方向相反,当导体形 状不变时,该两力平衡,因而,整个导线所受安培力 F = 2BIR j 题 10.20 解:(1)单位长度导线所受的安培力和静电力分别 为 fB = BI = d μ I 2π 2 0 fE = E = d C U 0 2 2 2π 由 fB+fE = 0 可得 d C U d I 0 2 2 2 0 2π 2π = 解得 I = 4.5 10 A 3 0 0 = CU