广东海洋大学：《大学物理》课程教学资源（各章习题解答）第04章 刚体

愿41：一汽车发动机曲轴的转速在12s内由12×10'r:mm均匀的增如到27×0'r·m。 (1)求曲轴转动的角加速度：(2)在此时间内，曲轴转了多少转？ 题41解，(1)由于角速度。=2别(n为单位时间内的轮数)，根据角加速度的定义a=如 在匀麦速转动中角加速度为 a=-4=2-l=131g (2》发动机曲拍过的角度为 0=aw+m2=21=0+r 2 在128内由轴转过的圈数为 N-日.0+1-30圈 22 题42上某种电动机启动后转速随时间变化的关系为0=。-e),式中。-90md·s, r=20s。求：(1)1=60s时的转速：(2)角加速度随时间变化的规律，(3)启动后6.0s内 转过的圈数。 恩42解：(1)根据盟意中转速随时间的变化关系。将1=6.0s代入，即得 (2》角加速度随时间变化的规律为 a-p.4.4 (3)1=6.0s时转过的角度为 -o-f:'mi--xond 则1=6.0s时电动机转过的圈数 N-日-57图 2开 思43：如图所示，一通风机的转动部分以初角速度。，烧其轴转动，空气的阻力矩与角速度 成正比。比例系数C为一常量，若转动部分对其伯的转动惯量为」，月：《1)经过多少时间 后其转动角速度减少为初角速度的一半？(2)在此时间内共转过多少转？ 题43解：(1)通风机叶片所受的阻力矩为M=-C,由转动定律M=知，可得叶片的角 加速度为 a=p=-Ce（1) d山 根据初始条件对式《1)积分，有 出- 由于C和J均为常量，得

题 4.1：一汽车发动机曲轴的转速在 12 s 内由 3 1 1.2 10 r min −   均匀的增加到 3 1 2.7 10 r min −   。 （1）求曲轴转动的角加速度；（2）在此时间内，曲轴转了多少转？ 题 4.1 解：（1）由于角速度 =2n（n 为单位时间内的转数），根据角加速度的定义 dt d  = ， 在匀变速转动中角加速度为 ( ) 0 0 2 13.1 rad s 2 − =  − = − = t n n t     （2）发动机曲轴转过的角度为 t t t (n n )t 0 2 0 0 2 2 1 = + + = + =       在 12 s 内曲轴转过的圈数为 390 圈 2 2 0 = + = = t n n N   题 4.2：某种电动机启动后转速随时间变化的关系为 (1 ) 0    t e − = − ，式中 1 0 9.0 rad s −  =  ，  = 2.0 s 。求：（1） t = 6.0 s 时的转速；（2）角加速度随时间变化的规律；（3）启动后 6.0 s 内 转过的圈数。 题 4.2 解：（1）根据题意中转速随时间的变化关系，将 t = 6.0 s 代入，即得 1 0 0 1 0.95 8.6 s − − = =          = −   t e （2）角加速度随时间变化的规律为 0 2 2 4.5 s d d − − − = = = t t e e t      （3）t = 6.0 s 时转过的角度为 d 1 d 36.9 rad 6 0 0 6 0 =         = = −   s − t s t e t     则 t = 6.0 s 时电动机转过的圈数 5.87 圈 2 = =   N 题 4.3：如图所示，一通风机的转动部分以初角速度  0 绕其轴转动，空气的阻力矩与角速度 成正比，比例系数 C 为一常量。若转动部分对其轴的转动惯量为 J ，问：（1）经过多少时间 后其转动角速度减少为初角速度的一半？（2）在此时间内共转过多少转？ 题 4.3 解：（1）通风机叶片所受的阻力矩为 M = −Cω ，由转动定律 M = Jα ，可得叶片的角 加速度为 J C t    = = − d d （1） 根据初始条件对式（1）积分，有   = −    0 0 d d d t t J C t 由于 C 和 J 均为常量，得

aane 当角速度由气→岛，时，转动所需的时问为 1=n2 (2)服据初始条件对式(2)积分，有 Jd0-JoeTa 即 0:是 在时间：内所转过的图数为 x.0.@ “新 题44：一燃气轮机在试车时，燃气作用在锅轮上的力矩为2.心×0'N:m,祸轮的转动惯量 为250kg■2。当轮的转速由2知x10'rmm4增大到1.12x10rm时，所经历的时间为 多少？ 题44解在匀变速转动中，角加速度红-包-鸟，由轮动定律M=a,可得飞轮所经历 的时间 1-0-色j-2-风）-085 解2：飞轮在恒外力矩作用下，根据角动量定理，有 灿-o-) 则 1=”=-小08 题45：用落体观察法测定飞轮的其动顺量，是将半径为R的飞轮支承在O点上，然后在绕 过飞轮的蝇子的一端挂一场量为m的重物，令重物以初速度为零下落，带动飞轮转动，记下 重物下落的距离和时间，就可算出飞轮的转动惯量。试写出它的计算式。（假设轴承闻无摩 擦) 恩4.5解1：设绳子的拉力为F,对飞轮而言，根据转动定律。有 FR-Ja 而对重物而言，由牛顿定律，有 限-=面(2) 由于绳子不可伸长，因此，有 77777777 a=R在(3》 重物作匀如速下落，则有 h-ar (4) 2

t J C e −  =0 当角速度由 0 0 2 1  →  时，转动所需的时间为 ln 2 C J t = （2）根据初始条件对式（2）积分，有   − = t t J C e t 0 0 0 d  d  即 C J 2 0  = 在时间 t 内所转过的圈数为 C J N     2 4 0 = = 题 4.4：一燃气轮机在试车时，燃气作用在涡轮上的力矩为 2.03 10 N m 3   ，涡轮的转动惯量 为 2 25.0 kg m 。当轮的转速由 3 1 2.80 10 r min −   增大到 4 1 1.12 10 r min −   时，所经历的时间为 多少？ 题 4.4 解 1：在匀变速转动中，角加速度 t  0  − = ，由转动定律 M = Jα ，可得飞轮所经历 的时间 ( ) 10.8 s 2 0 0 = − = − = n n M J J M t    解 2：飞轮在恒外力矩作用下，根据角动量定理，有 ( ) 0 0 d =  −  M t J t 则 ( ) 10.8 s 2 0 0 = − = − = n n M J J M t    题 4.5：用落体观察法测定飞轮的转动惯量，是将半径为 R 的飞轮支承在 O 点上，然后在绕 过飞轮的绳子的一端挂一质量为 m 的重物，令重物以初速度为零下落，带动飞轮转动，记下 重物下落的距离和时间，就可算出飞轮的转动惯量。试写出它的计算式。（假设轴承间无摩 擦） 题 4.5 解 1：设绳子的拉力为 FT，对飞轮而言，根据转动定律，有 FTR = J 而对重物而言，由牛顿定律，有 mg − FT = ma （2） 由于绳子不可伸长，因此，有 a = R （3） 重物作匀加速下落，则有 2 2 1 h = at （4）

由上述各式可解得飞轮的转动惯量为 层-到 解2：根据系统的机械能守恒定律，有 -e+m2+w=0r 2 而线速度和角速度的关系为 T=R信(2') 又根据重物作匀如速运动时，有 v=u(岁) 2=2() 由上述各式可得 m-可 若轴承处存在厚擦，上述测量转动惯量的方法仍可采用。这时，只雷通过用两个不同质 量的置物做两次测量即可消除摩擦力矩蒂米的影响。 题46：一飞轮由一直径为0cm,厚度为2.0em的属盘和两个直径为10cm,长为80em的 共轴圆柱体组成，设飞轮的密度为78×0g·m，求飞轮对轴的转动领量。 恩46解：根据转动惯量的叠如性，由匀质圆盘、圆桂 体对轴的转动赞量公式可得 =+=* 题47：如图所示，圆世的质量为m,半径为R。求它对O轴（即通过属盘边峰且平行于 盘中心轴)的转动惯量。 题47解：根据平行轴定理J。一J。◆m成和绕圆盘中心轴0的 转动惯量。一2m?可符 g-+威. 题《多试证明质量为网，半径为R的均匀球体，以直径为转轴的转动惯量为服'。如以 和球体相切的线为轴。其转动惯量又为多少？ 题4,8延：如图所示，图中阴影部分的小圆盘对OO轴的转动榄量为 w-ro-e-he-rh

由上述各式可解得飞轮的转动惯量为         = −1 2 2 2 h gt J mR 解 2：根据系统的机械能守恒定律，有 0 2 1 2 1 2 2 − mgh + mv + J = （1） 而线速度和角速度的关系为 v = R （2） 又根据重物作匀加速运动时，有 v = at （3） v 2ah 2 = （4） 由上述各式可得         = −1 2 2 2 h gt J mR 若轴承处存在摩擦，上述测量转动惯量的方法仍可采用。这时，只需通过用两个不同质 量的重物做两次测量即可消除摩擦力矩带来的影响。 题 4.6：一飞轮由一直径为 30 cm ，厚度为 2.0 cm 的圆盘和两个直径为 10 cm ，长为 8.0 cm 的 共轴圆柱体组成，设飞轮的密度为 3 3 7.8 10 kg m −   ，求飞轮对轴的转动惯量。 题 4.6 解：根据转动惯量的叠加性，由匀质圆盘、圆柱 体对轴的转动惯量公式可得 4 2 2 4 1 2 2 2 2 1 1 2 1 0.136 kg m 2 1 16 1 2 2 1 2 2 1 2  =       = +        +      = + =  ld ad d m d J J J m  题 4.7：如图所示，圆盘的质量为 m ，半径为 R 。求它对 OO 轴（即通过圆盘边缘且平行于 盘中心轴）的转动惯量。 题 4.7 解：根据平行轴定理 2 J O = J O + mR 和绕圆盘中心轴 O 的 转动惯量 2 O 2 1 J = mR 可得 2 2 2 2 O O 2 3 2 1 J  = J + mR = mR + mR + mR 题 4.8：试证明质量为 m ，半径为 R 的均匀球体，以直径为转轴的转动惯量为 2 5 2 mR 。如以 和球体相切的线为轴，其转动惯量又为多少？ 题 4.8 证：如图所示，图中阴影部分的小圆盘对 OO轴的转动惯量为 J r m (R x ) (R x )dx 2 1 d 2 1 d 2 2 2 2 2 = = −  −

式中。一品为匀质球体的密度。则球体以其直径00方转 轴的转动惯量为 J-jw-ple-ra-子e 5 又由平行轴定理可得球绕O,01轴的转动惯量为 =J+m2=2m 题4身质量面密度为。的均匀矩形板。试证其对与板面垂直的，通过几何中心的拍线的转 动损量为只+b)。其中1为矩形板的长，5为它的宽。 12 题49正取如图所示坐标，在板上取一质元dw=d时： 它对与板面垂直的，通过几何中心的轴线的转动候量为 d山-2+y2d 整个矩形板对该轴的转动惯量为 J=w=∫f2+= 五a+b) 思410：如图所示，质量属=l6的实心圆柱体A,其半径为r=15m,可以绕其固定水 平轴转动，阻力忽略不计。一条轻的柔绳绕在圆柱体上，其另一端系一个质量m:-80g的 物体B。求：(1)物体由静止开始下降10s后的距离：(2)绳的张力F,· 恩4,0解：(1)分别作两物体的受力分析图。对实心柱体而言，由转动定律得 Fr-ja-imr'a (1) 对悬挂物体面言，依据牛领定律，有 -F程=思8-F=,4(2) 且F=子。又由角量与线量的关系。得 aara 解上述方程组。可得物体下落的加速度 a=2mg m,+2m 在1=1.0s时，B下落的距离为 =m=s245m 属+2m (2)由式《2)可得绳中的张力为 5=g-小-mg=92N 周十2m3 题41山：质量为四，和m:的两物体A、B分别是挂在如图所示的组合轮两端。设两轮的半径 分别为R和，两轮的转动惯量分别为J,和：，轮与轴承间、绳索与轮间的摩擦力均略去 不计，绳的质量也略去不计，试求两物体的加速度和绳的张力： 题411解：分别对两物体及组合轮作受力分析，根据质点的牛顿定律和刚体的转动定律

式中 3 4 3 R m   = 为匀质球体的密度。则球体以其直径 OO为转 轴的转动惯量为 ( ) 2 2 2 2 5 2 d 2 1 J dJ R x x mR R R = = − =  −  又由平行轴定理可得球绕 O1O1 轴的转动惯量为 2 2 5 7 J  = J + mR = mR 题 4.9：质量面密度为  的均匀矩形板，试证其对与板面垂直的，通过几何中心的轴线的转 动惯量为 ( ) 12 2 2 lb l + b  。其中 l 为矩形板的长， b 为它的宽。 题 4.9 证：取如图所示坐标，在板上取一质元 dm =dxdy ， 它对与板面垂直的，通过几何中心的轴线的转动惯量为 dJ (x y ) dxdy 2 2 = +  整个矩形板对该轴的转动惯量为 ( ) ( )    − − = = + = + 2 2 2 2 2 2 2 2 12 1 J d d d l l b J b x y  x y lb l b 题 4.10：如图所示，质量 m1 =16 kg 的实心圆柱体 A ，其半径为 r =15 cm ，可以绕其固定水 平轴转动，阻力忽略不计。一条轻的柔绳绕在圆柱体上，其另一端系一个质量 m2 = 8.0 kg 的 物体 B 。求：（1）物体由静止开始下降 1.0 s 后的距离；（2）绳的张力 FT 。 题 4.10 解：（1）分别作两物体的受力分析图。对实心圆柱体而言，由转动定律得   2 T 1 2 1 F r = J = m r （1） 对悬挂物体而言，依据牛顿定律，有 P2 − FT  = m2 g − FT  = m2a （2） 且 FT FT =  。又由角量与线量的关系，得 a = r 解上述方程组，可得物体下落的加速度 1 2 2 2 2 m m m g a + = 在 t = 1.0 s 时，B 下落的距离为 2.45 m 2 2 1 1 2 2 2 2 = + = = m m m gt s at （2）由式（2）可得绳中的张力为 ( ) 39.2 N 1 2 2 1 2 = + = − = g m m m m FT m g a 题 4.11：质量为 m1 和 m2 的两物体 A、B 分别悬挂在如图所示的组合轮两端。设两轮的半径 分别为 R 和 r ，两轮的转动惯量分别为 1 J 和 2 J ，轮与轴承间、绳索与轮间的摩擦力均略去 不计，绳的质量也略去不计。试求两物体的加速度和绳的张力。 题 4.11 解：分别对两物体及组合轮作受力分析，根据质点的牛顿定律和刚体的转动定律

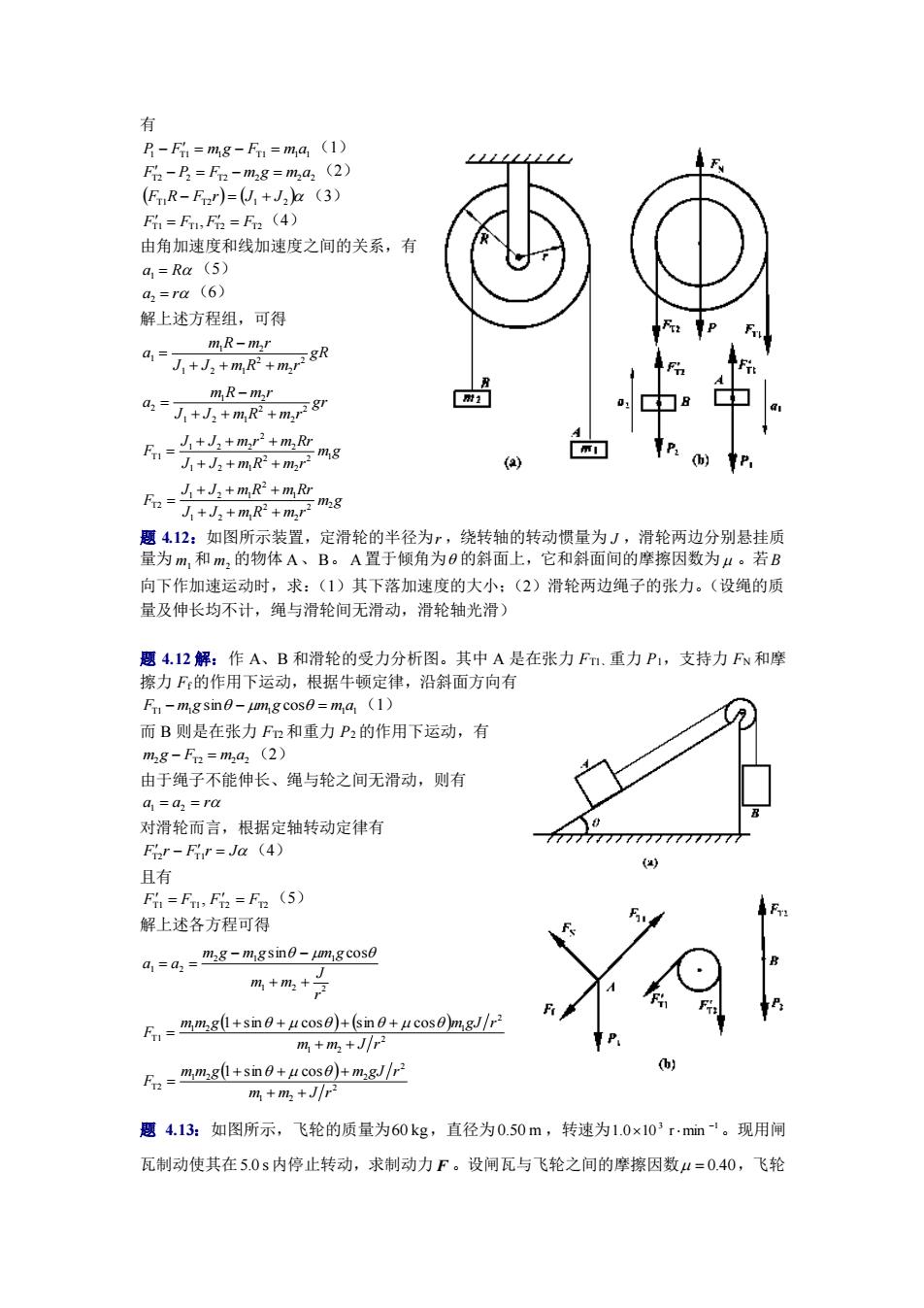
有 -=mg-F,=m4(1) 名-月=F-周8=m4(2) (ER-F小-+z(3) 吊=F=F(4) 由角加速度和线加速度之间的关系。有 4=Ra(5) 马=rg(6) 解上述方程组，可得 展R一图F +人*所用+他了8吸 ■ 思R=出，P 品“++及+周了 ,=++m2+m心 +人+网母+网子8 器 题412：如图所示装置，定滑轮的半径为r,饶转轴的转动惯量为J,滑轮两边分别悬挂质 量为围，和m的物体A、B。A置于顿角为的斜面上，它和斜面间的摩摄因数为丛·若B 向下作如速运动时，求：()其下落如速度的大小：(2》滑轮两边绳子的张力，（设绳的质 量及伸长均不计，绳与带轮间无滑动。滑轮轴光滑) 题4,12解：作A,B和滑轮的受力分析图。其中A是在张力F.重力P:支持力Fx和摩 擦力FP的作用下运动，根据牛顿定律，沿斜面方向有 F-周gsnB-%g88=mA(1) 而B则是在张力F?和重力P:的作用下运动，有 mg-=周4(2) 由干绳子不能伸长、绳与轮之间无滑动，则有 4=马-a 对滑轮而言，根据定轴转动定律有 F-F=a(4) 且有 =Fn.F品=Fm(5) 解上述各方程可得 马-4，-您8-mg5h0-四gs0 两+网+ F-mg+sn0+pcoso)+(sn+ucos0m 码+吗+ Fa-画+m9+2cs+画利止 群◆所*JP 题4,1为如图所示，飞轮的质量为60kg,直径为050m,转速为1.0×0'-m。现用闸 瓦制动使其在50s内停止转动，求制动力F。设闸瓦与飞轮之间的摩擦因数以=040，飞轮

有 P1 FT1 = m1g − FT1 = m1a1 −  （1） FT2 − P2 = FT2 − m2 g = m2a2  （2） (FT1R − FT2r) = (J1 + J 2 ) （3） T1 T1 T2 T2 F = F , F = F （4） 由角加速度和线加速度之间的关系，有 a1 = R （5） a2 = r （6） 解上述方程组，可得 gR J J m R m r m R m r a 2 2 2 1 2 1 1 2 1 + + + − = gr J J m R m r m R m r a 2 2 2 1 2 1 1 2 2 + + + − = m g J J m R m r J J m r m Rr F 2 1 2 2 1 2 1 2 2 1 2 2 T1 + + + + + + = m g J J m R m r J J m R m Rr F 2 2 2 2 1 2 1 1 2 1 2 1 T2 + + + + + + = 题 4.12：如图所示装置，定滑轮的半径为 r ，绕转轴的转动惯量为 J ，滑轮两边分别悬挂质 量为 m1 和 m2 的物体 A、B。 A 置于倾角为  的斜面上，它和斜面间的摩擦因数为  。若 B 向下作加速运动时，求：（1）其下落加速度的大小；（2）滑轮两边绳子的张力。（设绳的质 量及伸长均不计，绳与滑轮间无滑动，滑轮轴光滑） 题 4.12 解：作 A、B 和滑轮的受力分析图。其中 A 是在张力 FT1、重力 P1，支持力 FN 和摩 擦力 Ff的作用下运动，根据牛顿定律，沿斜面方向有 T1 1 1 1 1 F − m g sin − m g cos = m a （1） 而 B 则是在张力 FT2 和重力 P2 的作用下运动，有 m2 g − FT2 = m2a2 （2） 由于绳子不能伸长、绳与轮之间无滑动，则有 a1 = a2 = r 对滑轮而言，根据定轴转动定律有 FT2  r − FT1  r = J （4） 且有 T1 T1 T2 T2 F = F , F = F （5） 解上述各方程可得 1 2 2 2 1 1 1 2 sin cos r J m m m g m g m g a a + + − − = =    ( ) ( ) 2 1 2 2 1 2 1 T1 1 sin cos sin cos m m J r m m g m gJ r F + + + + + + =       ( ) 2 1 2 2 1 2 2 T2 1 sin cos m m J r m m g m gJ r F + + + + + =    题 4.13：如图所示，飞轮的质量为 60 kg ，直径为 0.50 m ，转速为 3 1 1.0 10 r min −   。现用闸 瓦制动使其在 5.0 s 内停止转动，求制动力 F 。设闸瓦与飞轮之间的摩擦因数  = 0.40 ，飞轮

质量全部分布在轮锋上。 题413解：飞轮和闸杆的受力分析如图所示，根据闸杆的 力矩平衡，有 +-以=0 面下=尽，则侧瓦作用于轮的摩擦力矩为 M-5号-出加D 24 摩擦力矩是恒力矩，飞轮作匀角加速转动，由转动的运动 规律，有 因飞轮的质量集中于轮缘，它绕轴的转动膜量/=4， 根据转动定律M=a,由式(1)，(2)可得制动力 F==34x02N +1 恩414：图是测试汽车轮酚滑动阻力的装置。轮胎最初为静止，且技一轻质框架支承者，轮 轴可绕点0自由转动，其转动惯量为05gm2,质量为15.0kg、半径为30.0cm。今将轮 胎故在以速率2.0ms移动的传送带上，并使概果AB保持水平。(1)如果轮胎与传送带之 间的动摩擦因数为060，则需要经过多长时间车轮才能达到最锋的角速度？(2)在传送带 上车胎滑动的粮迹长度是多少？ 题414解：车胎所受滑动摩擦力矩为 M-Amgr (1) 根据转动定律。车轮转动的角加速度为 a号 (2) 要使轮与带之间无相对滑动，车轮转动的角建度为 m=w(3) 开始时车轮静止，即风=0，故由匀加速转动提律。=鸟+园，可得 (4) 由上述各式可解得 小 =13, (2)在，时间内，轮缘上一点转过的弧长 n0-5 围传送带移动的距离1一。因此，传送带上滑痕的长度 d-1-1-n-Ir 1 2g产6m 题4,15一半轻为R、质量为用的匀质圆盘，以角速度。绕其中心轴转动，现将它平政在

质量全部分布在轮缘上。 题 4.13 解：飞轮和闸杆的受力分析如图所示。根据闸杆的 力矩平衡，有 F(l 1 + l 2 )− FN l 1 = 0 而 FN FN =  ，则闸瓦作用于轮的摩擦力矩为 F d l l l F d d M F   1 1 2 f N 2 2 1 2 + = = = （1） 摩擦力矩是恒力矩，飞轮作匀角加速转动，由转动的运动 规律，有 t n t t      0 0 2 = = − = （2） 因飞轮的质量集中于轮缘，它绕轴的转动惯量 4 2 J = md ， 根据转动定律 M = J ，由式（1）、（2）可得制动力 ( ) 3.14 10 N 2 1 2 1 =  + = l l t nmdl F   题 4.14：图是测试汽车轮胎滑动阻力的装置。轮胎最初为静止，且被一轻质框架支承者，轮 轴可绕点 O 自由转动，其转动惯量为 2 0.75 kg m 、质量为 15.0 kg 、半径为 30.0 cm 。今将轮 胎放在以速率 1 12.0 m s −  移动的传送带上，并使框架 AB 保持水平。（1）如果轮胎与传送带之 间的动摩擦因数为 0.60 ，则需要经过多长时间车轮才能达到最终的角速度？（2）在传送带 上车胎滑动的痕迹长度是多少？ 题 4.14 解：车胎所受滑动摩擦力矩为 M = mgr （1） 根据转动定律，车轮转动的角加速度为 J M  = （2） 要使轮与带之间无相对滑动，车轮转动的角速度为  = vr （3） 开始时车轮静止，即 0 = 0 ，故由匀加速转动规律  = +t 0 ，可得   t = (4) 由上述各式可解得 1.13 s 2 = = mgr Jv t  （2）在 t 时间内，轮缘上一点转过的弧长 2 2 t r s = r =  而传送带移动的距离 l = vt，因此，传送带上滑痕的长度 6.80 m 2 2 1 2 2 2 = − = − = = mgr Jv d l s vt r t   题 4.15：一半径为 R 、质量为 m 的匀质圆盘，以角速度  绕其中心轴转动，现将它平放在

一水平板上，盘与板表面的厚擦因数为“，(1)求周盘所受的厚挥力矩。(2)问经过多少时 间后，圆盘转动才能停止？ 题415解：(1)圆盘上半径为F、宽度为dr的同心圆环所受的摩擦力大小 d识一2应w过/成2，其方向与环的半径垂直，它的摩擦力矩为 dM=r×dF=2'sr/R)k 式中。为轴向的单位失量。圆盘所受的总厚擦力矩大小为 -fav (2)由于摩擦力矩是一恒力矩，盘的转动惯量/=成2。由角动量定理山-)： 可得额里停止的时同为 出=e-8 M 4g 题41：一质量为m'、半径为R的均匀圆查，通过其中心且与盘面垂直的水平轴以角速度： 转动，若在某时刻，一质量为m的小碎块从盘边锋裂开，且恰好沿垂直方向上抛。问它可能 达到的高度是多少？破裂后圆数的角动量为多大？ 题4.16解：(1)醉块抛出时的初速度为 6=9 由于碎块整直上抛运动，它所能到达的高度为 -发.e 2g 2g (2)圆盘在裂开的过程中，其角动量守恒。故有 L-4- 式中L,=。mR。为园盘未碎时的角动量：=。R。为碎块 被视为质点时，对轴的角动量：L为破裂后盘的角动量。则 L-(w-mea 恩417：在光滑的水平面上有一木杆。其质量为m,-10妈，长为1=40cm,可绕通过其中 点并与之垂直的轴转动，一质量为画-0g的子弹，以y一20x02ms的速度射入杆端， 其方向与杆及轴正交。若子弹陷入杆中，试求所得到的角速度。 题4.17解：根据角动量守恒定理 J=从+w 式中人=画，2了为子弹绕轴的转动惯量，J为 子弹在陷入杆前的角动量，台-21为子弹在此刻 绕轴的角速度。人=园户2为杆绕轴的转动柄量， 是子弹陷入杆后它门一起绕轴的角速度。可得

一水平板上，盘与板表面的摩擦因数为  。（1）求圆盘所受的摩擦力矩。（2）问经过多少时 间后，圆盘转动才能停止？ 题 4.15 解 ： （1）圆盘上半径为 r、 宽度为 dr 的同心圆 环所受的摩 擦力大小 2 dFf = 2rmgdr R ，其方向与环的半径垂直，它的摩擦力矩为 M r F ( ) k 2 2 d =  d f = − 2r mgdr R 式中 k 为轴向的单位矢量。圆盘所受的总摩擦力矩大小为   = = = R mgR R r mg r M M 0 2 2 3 2 d 2 d   （2）由于摩擦力矩是一恒力矩，圆盘的转动惯量 J = mR2 /2。由角动量定理 Mt = (J)， 可得圆盘停止的时间为 g R M J t    4 3  = = 题 4.16：一质量为 m  、半径为 R 的均匀圆盘，通过其中心且与盘面垂直的水平轴以角速度  转动，若在某时刻，一质量为 m 的小碎块从盘边缘裂开，且恰好沿垂直方向上抛，问它可能 达到的高度是多少？破裂后圆盘的角动量为多大？ 题 4.16 解：（1）碎块抛出时的初速度为 v0 =R 由于碎块竖直上抛运动，它所能到达的高度为 g R g v h 2 2 2 2 2 0  = = （2）圆盘在裂开的过程中，其角动量守恒，故有 L = L − L 0 式中  2 0 2 1 L = mR 为圆盘未碎时的角动量；  2 2 1 L = mR 为碎块 被视为质点时，对轴的角动量；L 为破裂后盘的角动量。则  2 2 1 L m mR      =  − 题 4.17：在光滑的水平面上有一木杆，其质量为 m1 =1.0 kg ，长为 l = 40 cm ，可绕通过其中 点并与之垂直的轴转动，一质量为 m2 =10 g 的子弹，以 2 1 2.0 10 m s − v =   的速度射入杆端， 其方向与杆及轴正交。若子弹陷入杆中，试求所得到的角速度。 题 4.17 解：根据角动量守恒定理  = ( + ) 2 1 2 J J J 式中 ( ) 2 J2 = m2 l 2 为子弹绕轴的转动惯量， J 2 为 子弹在陷入杆前的角动量，  = 2v l 为子弹在此刻 绕轴的角速度。 12 2 1 1 J = m l 为杆绕轴的转动惯量，  是子弹陷入杆后它们一起绕轴的角速度。可得

杆的角速度为 w-5o 6 +网+3g7 =291w 题418：率径分别为：、。与的两个潮◆形轮，它们各自对通过盘心且垂直盘而转轴的转动惯 量为山，和：·开始时轮I以角速度®，转动，问与轮Ⅱ成正交陆合后，两轮的角速度分别为 多大？ 题418解：设相互作用力为F,在响合的短时间山 内，根据角动量定理。对轮1、轮Ⅱ分别有 -mW=间-线)(1) M=J%(2) 两轮哺合后应有相同的线速度，故有 m=%(3) 由上述各式可解得味合后两轮的角速度分别为 鸟、5 晚 题41一质量为20.0妈的小孩，姑在一半径为300m,转动惯量为490gm的静止水平 转台的边修上，此转台可绕通过转台中心的经直触转动，转台与触间的摩擦不计，如果此小 孩相对转台以1.0ms的速率沿转台边峰行走，月转台的角速率有多大？ 题419解：没转台相对地的角速度为(，人相对转台的角速度为台。由相对角速度的美系， 人相对地面的角速度为 0=%+=风+发D 由于系统初始是静止的，根据系统的角动量守恒定律，有 J4+J%+=0(2》 式中人、山一m分别为转台、人对转台中心轴的转动惯量.由式(1)、(2》可得转台的角 速度为 8“,+m成京9纪0g 式中负号表示转台转动地方向与人对地面的转动方向相反。 题42：一转台饶其中心的竖直轴以角速度m。=常。转动。转台对转轴的转动惯量为 J,=4.00小名m2。今有砂整以0-立gs的流量整直落至转台，并粘阳于台而形成一圆 环，若环的率径为r=010m,求砂粒下落=10s时，转台的角速度。 题4.20解：在时间0→10s内落至台面的的粒的质量为 m-Q地-a0e 根据氛统的角动量守恒定律，有 J两=。+w）a

杆的角速度为 ( ) 1 1 2 2 1 2 2 29.1s 3 6 − = + = +  = m m l m v J J J   题 4.18：半径分别为 1 r 、 2 r 的两个薄伞形轮，它们各自对通过盘心且垂直盘面转轴的转动惯 量为 1 J 和 2 J 。开始时轮Ⅰ以角速度  0 转动，问与轮Ⅱ成正交啮合后，两轮的角速度分别为 多大？ 题 4.18 解：设相互作用力为 F，在啮合的短时间 t 内，根据角动量定理，对轮 I、轮 II 分别有 ( ) − 1 = 1 1 −0 Fr t J （1） 2 22 Fr t = J （2） 两轮啮合后应有相同的线速度，故有 11 22 r = r （3） 由上述各式可解得啮合后两轮的角速度分别为 2 2 1 2 1 2 1 0 1 2 2 2 2 1 2 1 2 2 1 0 2 1 , J r J r J rr J r J r J r + = + =     题 4.19：一质量为 20.0 kg 的小孩，站在一半径为 3.00m 、转动惯量为 2 450 kg m 的静止水平 转台的边缘上，此转台可绕通过转台中心的竖直轴转动，转台与轴间的摩擦不计。如果此小 孩相对转台以 1 1.00 m s −  的速率沿转台边缘行走，问转台的角速率有多大？ 题 4.19 解：设转台相对地的角速度为 0 ，人相对转台的角速度为 1 。由相对角速度的关系， 人相对地面的角速度为 R v  =0 +1 =0 + （1） 由于系统初始是静止的，根据系统的角动量守恒定律，有 J00 + J1 (0 +1 ) = 0 （2） 式中 J0、J1 = mR2 分别为转台、人对转台中心轴的转动惯量。由式（1）、（2）可得转台的角 速度为 2 1 2 0 2 0 9.52 10 s − − = −  + = − R v J mR mR  式中负号表示转台转动地方向与人对地面的转动方向相反。 题 4.20：一转台绕其中心的竖直轴以角速度 1 0 s −  =  转动，转台对转轴的转动惯量为 3 2 0 = 4.010 kg m − J 。今有砂粒以 1 2 g s − Q = t  的流量竖直落至转台，并粘附于台面形成一圆 环，若环的半径为 r = 0.10m ，求砂粒下落 t =10 s 时，转台的角速度。 题 4.20 解：在时间 0→10 s 内落至台面的砂粒的质量为 d 0.10 kg 10 s 0 = =  m Q t 根据系统的角动量守恒定律，有  ( ) 2 J 0 0 = J 0 + mr

则1=105时，转台的角速度 8--0.8ms 。+ 题42：为使运行中的飞船停止绕其中心轴的转动，可在飞船的侧面对称地安装两个切向控 制喷管，利用喷管高速喷射气体来制止蒙转。若飞船绕其中心轴的转动惯量 。=2.0×10'g~m2,旋转的角速度0=02dg,喷口与轴战之间的距离r=15m:骑气 以恒定的流量Q-10g%和速率：一0m等从喷口喷出，问为使该飞船停止装转，喷气应 喷射多长时阿？ 题421分析将飞船与喷出的气体作为研究系统。在喷气过程中，系统不受外力矩作用， 其角动量守恒。在列出方程时应注意：(1》由于骑气质量运小于飞船质量，晚气前，后系统 的角动量近似为飞船的角动量衡(2)喷气过程中气流速率#远大于飞船侧面的线速度 因此，整个喷气过程中，气流相树于空间的速率仍可近制看作是，这样，排出气体的总角 动量L=[仙+rw:w,经上述处理后，可使月题大大简化， 解：取飞船和喷出的气体为系统，根据角动量 守相定律，有 9-6r=0 因喷气的流量恒定，放有 m=20 由式《(1)、(2)可得喷气的境财时间为 1=是=2675 Cur 题422：一质量为网'、半径为R的转台，以角速度移转动，转轴的摩擦略去不计。(1)》有 一质量为m的始蛛垂直地落在转台边缘上。此时，转台的角速度母，为多少？(2》若蜘蛛面 后慢慢地爬向转台中心，当它离转台中心的距离为时，转台的角速度种，为多少？设蜘蛛 下落前距离转台很近。 恩422解：《1)始蛛垂直下落至转台边缘时，由系统的角动量守恒定律，有 J.-+s 式中人，=二m公为转台对其中心轴的转动惯量，人=m吸为期蛛刚落至台面边锋时，它对轴 的转动赞量。于是可得 4, (2》在蜘蛛向中心轴处慢慢爬行的过程中，其转动惯量将面半径F而改变，即3=。 在此过程中，由系统角动量守恒，有 J。=+ 则 R “+女8“mR+2m 题423一质量为1.12kg,长为10m的均匀细棒，义点在棒的上端点，开始时棒自由悬挂。 以100N的力打击它的下端点，打击时间为0.2s。(1)若打击前棒是静止的，求打击时其

则 t = 10 s 时，转台的角速度 1 2 0 0 0 0.8 s − = + =    J mr J 题 4.21：为使运行中的飞船停止绕其中心轴的转动，可在飞船的侧面对称地安装两个切向控 制喷管，利用喷管高速喷射气体来制止旋转。若飞船绕其中心轴的转动惯量 3 2 J 0 = 2.010 kg m ，旋转的角速度 1 0.2 rad s −  =  ，喷口与轴线之间的距离 r =1.5 m ；喷气 以恒定的流量 1 1.0 kg s − Q =  和速率 1 50 m s − u =  从喷口喷出，问为使该飞船停止旋转，喷气应 喷射多长时间？ 题 4.21 分析：将飞船与喷出的气体作为研究系统，在喷气过程中，系统不受外力矩作用， 其角动量守恒。在列出方程时应注意：（1）由于喷气质量远小于飞船质量，喷气前、后系统 的角动量近似为飞船的角动量 J；（2）喷气过程中气流速率 u 远大于飞船侧面的线速度r， 因此，整个喷气过程中，气流相对于空间的速率仍可近似看作是 u，这样，排出气体的总角 动量 L (u r) m mur m = +    d 。经上述处理后，可使问题大大简化。 解：取飞船和喷出的气体为系统，根据角动量 守恒定律，有 J − mur = 0 因喷气的流量恒定，故有 m = 2Qt 由式（1）、（2）可得喷气的喷射时间为 = = 2.67 s Qur J t  题 4.22：一质量为 m  、半径为 R 的转台，以角速度  a 转动，转轴的摩擦略去不计。（1）有 一质量为 m 的蜘蛛垂直地落在转台边缘上。此时，转台的角速度  b 为多少？（2）若蜘蛛随 后慢慢地爬向转台中心，当它离转台中心的距离为 r 时，转台的角速度  c 为多少？设蜘蛛 下落前距离转台很近。 题 4.22 解：（1）蜘蛛垂直下落至转台边缘时，由系统的角动量守恒定律，有 ( ) 0a 0 1 b J = J + J 式中 2 0 2 1 J = mR 为转台对其中心轴的转动惯量， 2 J1 = mR 为蜘蛛刚落至台面边缘时，它对轴 的转动惯量。于是可得 a a 0 1 0 b 2    m m m J J J  +  = + = （2）在蜘蛛向中心轴处慢慢爬行的过程中，其转动惯量将随半径 r 而改变，即 2 J 2 = mr 。 在此过程中，由系统角动量守恒，有 ( ) 0a 0 2 c J = J + J 则 2 2 a 2 a 0 2 0 c 2    m R mr m R J J J  +  = + = 题 4.23：一质量为 1.12 kg ，长为 1.0 m 的均匀细棒，支点在棒的上端点，开始时棒自由悬挂。 以 100 N 的力打击它的下端点，打击时间为 0.02 s 。（1）若打击前棒是静止的，求打击时其

角动量的变化：(2》棒的最大偏转角。 题423解：(1)在厨间打击过程中。由刚体的角动量定理得 L=J网=J仙=F7M=2.0gm.s(1) (2)在棒的转动过程中，取棒和地球为一系统。并透0处为重 力势能零点。在转动过程中，系统的机械能守恒，即 o-cou)(2) 由式(1)、(2)可得棒的偏转角度为 3FAr 0-arccos 1- -838 题424：(1)设氢原子中电子在圆形轨道中以速率，绕质子运动，作用在电子上的向心力为 电作用力，其大小为214c一2，其中为电子、质子的电量，？为轨道华径，6，为恒量。 试证轨道半径为 ra- e 4原，m (2》假设电子绕核的角动量只能为/2x的整数倍，其中6为普朗克常量，试证电子的可能 轨道率径由下式确定： ra- 2em (3》试由以上两式消去，，从而证明符合这两个要求的轨道半径必须满足以下关系式 -月c,h r=- 式w中可取正整数1,2.3， 题424证：(1)电子绕质子作圆周运动的向心力是它们之间的电作用力F= 4 :(可略去 万有引力)，根据径向动力学方程F=m,有 常了 则电子的轨道半径为 rs-e 4.E w (2)根紧愿中电子角动量的量子化条件，即1= " ,有 m子 L-aN 2■ 则电子可能的轨道率径为 典 (3)根据《1)和(2)的结果消去，电子可能的轨道半径也可表示为

角动量的变化；（2）棒的最大偏转角。 题 4.23 解：（1）在瞬间打击过程中，由刚体的角动量定理得 2 1 0 d 2.0 kg m s −  = = =  =    L J M t Fl t （1） （2）在棒的转动过程中，取棒和地球为一系统，并选 O 处为重 力势能零点。在转动过程中，系统的机械能守恒，即  (1 cos ) 2 1 2 1 2 J 0 = mgl − （2） 由式（1）、（2）可得棒的偏转角度为 88 38 3 arccos 1 2 2 2 =           = −  m gl F t  题 4.24：（1）设氢原子中电子在圆形轨道中以速率 v 绕质子运动。作用在电子上的向心力为 电作用力，其大小为 2 0 2 e / 4 r ，其中 e 为电子、质子的电量， r 为轨道半径， 0  为恒量。 试证轨道半径为 2 0 2 4 mv e r  = （2）假设电子绕核的角动量只能为 h / 2 的整数倍，其中 h 为普朗克常量。试证电子的可能 轨道半径由下式确定： mv nh r 2 = （3）试由以上两式消去 v ，从而证明符合这两个要求的轨道半径必须满足以下关系式： 2 2 0 2 me n h r   = 式 n 中可取正整数 1, 2, 3。 题 4.24 证：（1）电子绕质子作圆周运动的向心力是它们之间的电作用力 2 0 2 4 r e F  = （可略去 万有引力），根据径向动力学方程 F = man，有 r mv r e 2 2 0 2 4 =  则电子的轨道半径为 2 0 2 4 mv e r  = （2）根据题中电子角动量的量子化条件，即 2 h L = n ，有 4 2 2 0 2 h n mv e L = mv = 则电子可能的轨道半径为 mv nh r 2 = （3）根据（1）和（2）的结果消去 v，电子可能的轨道半径也可表示为