13机橘扳对解答 13-1 0可通过关系式心一三确定。报子运动的速度 和加速度的计算仍与质点运功学中的计算方法 相. 解因四-,则运动方程 Av 积据震中给出的爱据得 x=()cos[2ay+0.75] 雨子的速度和加速度分别为 p-在1i-4r×10'mg)sm2s'y+0.75网 a-子x/h2--8r2×102mscs2mw+05 rt、t及t图如图13-1所示 132若前谐运动方程为x=0,01m)c20'+引求:()振,危半,同期 初相:(2)12s时的位移、速度和加速度。 代入(战后,即可求得结果。 解(1)将=0.10es2Dr+0.251与-ad+)比较后可得,报相A=0.10 ,角车8=20,制相=025x,则期T-21-01s,领率-1T-10。 (2》=2s时的他移、建度、加建度分别为 x-0.10m)0s40+0.25g1-7.07×102m
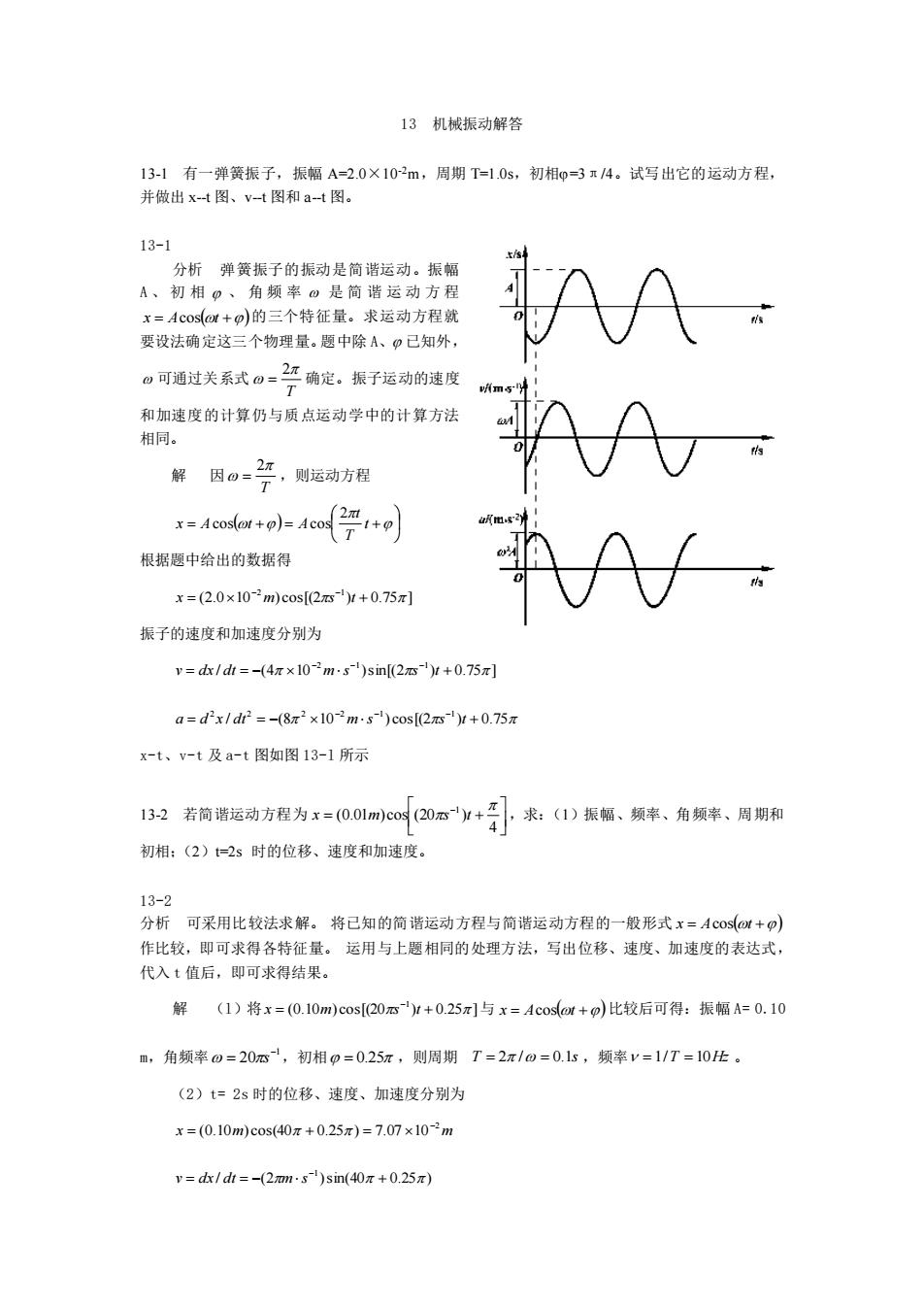
13 机械振动解答 13-1 有一弹簧振子,振幅 A=2.0×10-2m,周期 T=1.0s,初相=3π/4。试写出它的运动方程, 并做出 x--t 图、v--t 图和 a--t 图。 13-1 分析 弹簧振子的振动是简谐运动。振幅 A 、 初 相 、 角 频 率 是 简 谐 运 动 方 程 x = Acos(t +) 的三个特征量。求运动方程就 要设法确定这三个物理量。题中除 A、 已知外, 可通过关系式 T 2 = 确定。振子运动的速度 和加速度的计算仍与质点运动学中的计算方法 相同。 解 因 T 2 = ,则运动方程 ( ) = + = + t T t x A t A 2 cos cos 根据题中给出的数据得 (2.0 10 ) cos[(2 ) 0.75 ] 2 1 = + − − x m s t 振子的速度和加速度分别为 / (4 10 )sin[(2 ) 0.75 ] 2 1 1 = = − + − − − v dx dt m s s t / (8 10 ) cos[(2 ) 0.75 2 2 2 2 1 1 = = − + − − − a d x dt m s s t x-t、v-t 及 a-t 图如图 13-l 所示 13-2 若简谐运动方程为 = + − 4 (0.01 )cos (20 ) 1 x m s t ,求:(1)振幅、频率、角频率、周期和 初相;(2)t=2s 时的位移、速度和加速度。 13-2 分析 可采用比较法求解。 将已知的简谐运动方程与简谐运动方程的一般形式 x = Acos(t +) 作比较,即可求得各特征量。 运用与上题相同的处理方法,写出位移、速度、加速度的表达式, 代入 t 值后,即可求得结果。 解 (l)将 (0.10 ) cos[(20 ) 0.25 ] 1 = + − x m s t 与 x = Acos(t +) 比较后可得:振幅 A= 0.10 m,角频率 1 20 − = s ,初相 = 0.25 ,则周期 T = 2 / = 0.1s ,频率 = 1/T = 10Hz 。 (2)t= 2s 时的位移、速度、加速度分别为 x m m 2 (0.10 ) cos(40 0.25 ) 7.07 10 − = + = / (2 )sin(40 0.25 ) 1 = = − + − v dx dt m s

a=dx/h=-40r2m-g9)6(40x+025x} 133没地绿是一个半径为R的均匀球体,密度P5.5×10kg■”。现假定沿直径带一条隧道, 看有一质量为■的质点在此魔道内做无摩擦运动:《1)正明此质点的运动是商请据动:(2)计算 其周期, 13-3 分析正明方法与上题相叙,分析质点在随道内运动时的受力特任围可, 证《1》取图13-3所示坐标。当质量为■的质点位于1处时,它受地保的明力为 F=-G四m 式中G为引力常量,画,是以玉为半轻的球体频量,即围,=4p3。令素=4Gm3,则顺点受 力 F=-4XGim /3=-kx 因此,质点作简谐话动, 《2)质点量功的周期为 T=2mlk =3/Gp =5.07x10'x 13-4如图所示,两个轻弹簧的动度系数分别为k,和k,物体在光滑料面上振动。(1)证明其 运动仍是简错振动:(2)采系统的振动频率。 0 a ) 13-4
/ (40 ) cos(40 0.25 ) 2 2 2 2 = = − + − a d x dt m s 13-3 设地球是一个半径为 R 的均匀球体,密度ρ5.5×103kg• m -3。现假定沿直径凿一条隧道。 若有一质量为 m 的质点在此隧道内做无摩擦运动。(1)证明此质点的运动是简谐振动;(2)计算 其周期。 13-3 分析 证明方法与上题相似。 分析质点在隧道内运动时的受力特征即可。 证(l)取图 13-3 所示坐标。 当质量为 m 的质点位于 x 处时,它受地球的引力为 2 x m m F G x = − 式中 G 为引力常量,mx 是以 x 为半径的球体质量,即 4 / 3 3 m x x = 。令 k = 4Gm / 3 ,则质点受 力 F = −4Gmx / 3 = −kx 因此,质点作简谐运动。 (2)质点振动的周期为 s T m k G 3 5.07 10 2 / 3 / = = = 13-4 如图所示,两个轻弹簧的劲度系数分别为 k1 和 k2,物体在光滑斜面上振动。(1)证明其 运动仍是简谐振动;(2)求系统的振动频率。 13-4

分析从上两愿的零解知道,要旺明一个系统作简谐运动,首先要分析受力情况,然后看是否端 足简请运动的受力特征《或简谐运动微分方程.为此,建立如图13-4《6)所示的坐标。设 系统平衡时物体所在位置为坐标原点0,0x轴正向沿斜面向下,由受力分新可知,沿0x轴,物 体受弹性力及重力分力的作用,其中弹性力是变力。利用串颗时各弹簧受力相等。分析物体在 任一位置时受力与位移的关系,即可正得物体作箭谐运动,并可求出绳率。 证设物体平衡时两弹簧伸长分别为,:则由物体受力平衡,有 gsn0=k=k高 按图()所取坐标,物体沿x轴移动位移x时,两弹簧又分别枝拉伸'和',即x=无+': 则物体受力为 F=限sn8-k(馬1+无)=wsnB-k(馬+高) 将式(1)代人式(2)得 下=k=-k 由式(3)得=-F/h、=-下/气,而x=+x。则得到 F■-kkk+k灯■-红 式中=,人风人+k》为觉数,则物体作简请运动,振动频率 -a2-名-立帖+6m 讨论(1)由本题的求证可知,斜面领角对弹簧是否作简诱运动以及量动的顿率均不产生 影响。事实上,无论弹簧水平放置、斜置还是极直是挂,物体均作前萧运动。面且可以证明它 们的期零相同。均由弹簧振子的国有性质决定,这就是称为固有频率的原因。(2)如零振动系 统如图13-4(©》(弹簧并联)或如图13-4(d)所示,也可通过物体在某一位置的受力分析得出 其作简谐运功,且佩功频常均为= 244 e d 读者可以一试。通过这些例子可以知道,证明物体是否作简请运动的思路是相同的 135为了测得一物体得质量m,将其挂在一弹簧上让其白由振动。测得振动顿率片=10比。 而将另一质量w一0幼g的物体单独挂在该弹簧上时,测得振动频率一20壮。设据动均在弹 需的弹性限度内走行,求被测物体的质量。 13-6 分析物体挂在弹簧上组成弹责扳子系统。其银动顿率=、需,即x网。采用比较 须常?的方法可求出来知物体的质量, 解由分析可知,Px√m,则有叫华一√侧/网。根据题中给指的数据可得物体的质
分析 从上两题的求解知道,要证明一个系统作简谐运动,首先要分析受力情况,然后看是否满 足简谐运动的受力特征(或简谐运动微分方程)。 为此,建立如图 13-4(b)所示的坐标。 设 系统平衡时物体所在位置为坐标原点 O,Ox 轴正向沿斜面向下,由受力分析可知,沿 Ox 轴,物 体受弹性力及重力分力的作用,其中弹性力是变力。 利用串联时各弹簧受力相等,分析物体在 任一位置时受力与位移的关系,即可证得物体作简谐运动,并可求出频率 。 证 设物体平衡时两弹簧伸长分别为 x1、x2,则由物体受力平衡,有 1 1 2 2 mg sin = k x = k x 按图(b)所取坐标,物体沿 x 轴移动位移 x 时,两弹簧又分别被拉伸 ' 1 x 和 ' 2 x ,即 ' ' 1 2 x = x +x 。 则物体受力为 sin ( ') sin ( ') 2 2 2 1 1 1 F = mg − k x + x = mg − k x + x 将式(1)代人式(2)得 ' ' 1 1 2 2 F = −k x = −k x 由式(3)得 1 1 2 2 x ' = −F / k、x ' = −F / k ,而 ' ' 1 2 x = x +x ,则得到 F = −k k /(k + k )x = −kx 1 2 1 2 式中 /( ) 1 2 1 2 k = k k k + k 为常数,则物体作简谐运动,振动频率 k m k k /(k k )/ m 2 1 / 2 1 = / 2 = = 1 2 1 + 2 讨论(1)由本题的求证可知,斜面倾角 对弹簧是否作简谐运动以及振动的频率均不产生 影响。 事实上,无论弹簧水平放置、斜置还是竖直悬挂,物体均作简谐运动。 而且可以证明它 们的频率相同,均由弹簧振子的固有性质决定,这就是称为固有频率的原因。 (2)如果振动系 统如图 13-4(c)(弹簧并联)或如图 13-4(d)所示,也可通过物体在某一位置的受力分析得出 其作简谐运动,且振动频率均为 (k k )/m 2 1 = 1 + 2 读者可以一试。 通过这些例子可以知道,证明物体是否作简谐运动的思路是相同的 13-5 为了测得一物体得质量 m,将其挂在一弹簧上让其自由振动,测得振动频率 1.0Hz 1 = 。 而将另一质量 m 0.5kg ' = 的物体单独挂在该弹簧上时,测得振动频率 2.0Hz 2 = 。设振动均在弹 簧的弹性限度内进行,求被测物体的质量。 13-5 分析 物体挂在弹簧上组成弹簧振子系统,其振动频率 k / m 2 1 = ,即 1/m 。采用比较 频率 的方法可求出未知物体的质量。 解 由分析可知, 1/m ,则有 1 / 2 = m'/ m 。 根据题中绘出的数据可得物体的质
量为 周=时(5/)2-20k家 136在如图所示的装置中,一动度系数为k的弹簧。一端固定在塘上,另一编连接一质量为 m,的物体A,置于光滑水平桌面上。现通过一质量为m、半径为R的定滑轮B(可棍为匀质圆 盘)用细绳连接另一质量为一:的物体C,设细绳不可种长,且与滑轮间无相对滑动,象系统的 探动角频事。 13-6 分析这是一个由弹簧、物体A、C和滑轮B粗成的简语运动系统。求解系统的雨动频事 可采用两种方法。(1)从受力分析着手。如图13-6()所示,设系统处于平衡状态时,与 物体A相连的弹簧一端所在位置为坐标原点0,此时弹簧已种长:且气=网g。当弹爵沿0: 轴正向从原点D钟长x时,分析物体A,及滑轮B的受力情况,并分别列出它们的动力学方程, 可解得系统作简谐运动的微分方程。(2》从系统机械能守恒看于。列出系统机械能守恒方程, 然后求得系绕作简谐运动的做分方程。 e 解1在图13-6(6)的状志下,各物棒受力如图13-5(c)所示。其中F=-Mx+F。 考虑到绳子不可伸长,对物体A,B,分别方程,有 dx B,-+)=m (1 典82-偶 (20 39 作-FnR-e-号m (3) 气思8 (4) 方程(3)中用到了Fn=F,'、F:=F:'./=成2,及a=g/R。联立式(1)-式(4) 可得
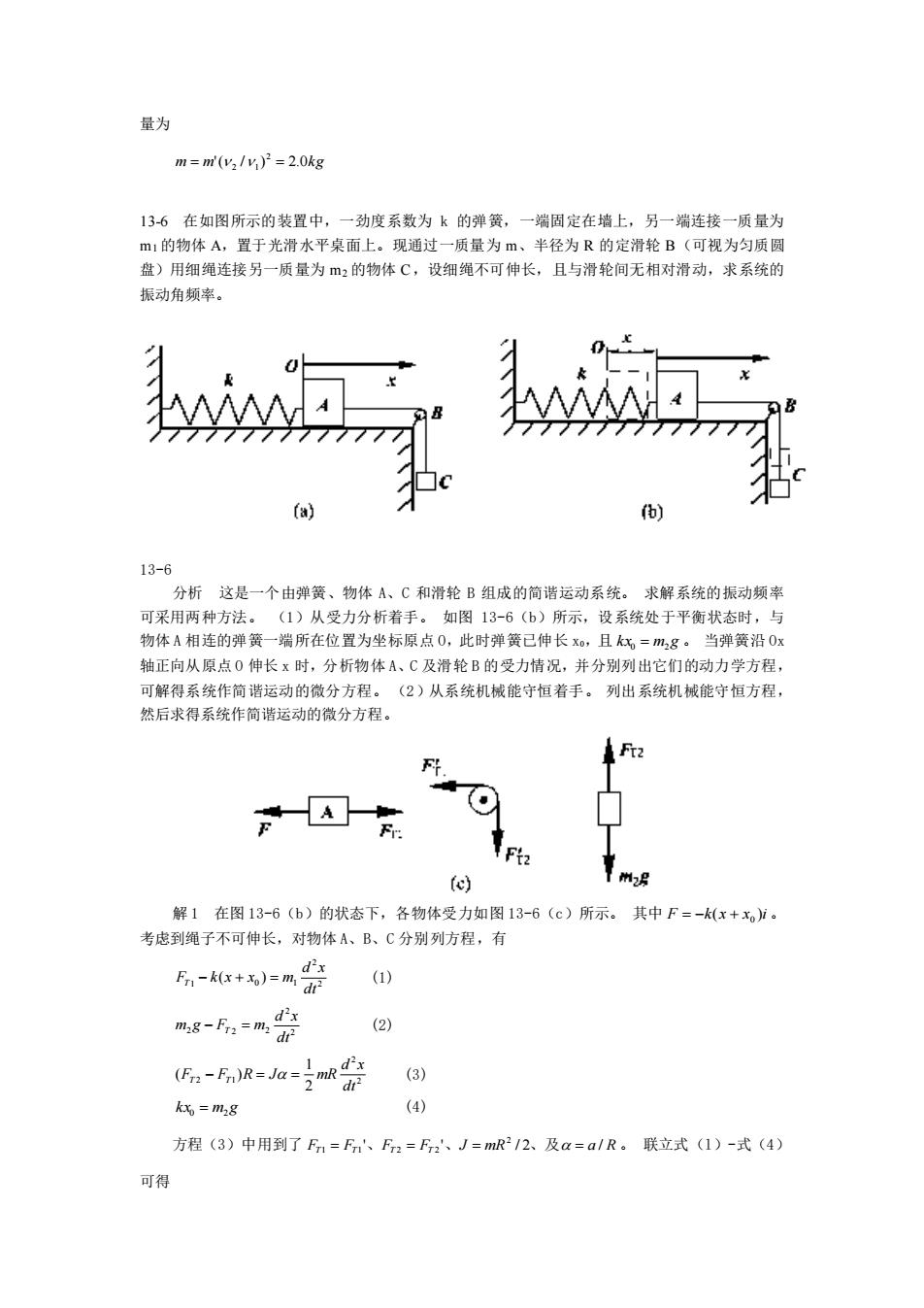
量为 m m'( / ) 2.0k g 2 = 2 1 = 13-6 在如图所示的装置中,一劲度系数为 k 的弹簧,一端固定在墙上,另一端连接一质量为 m1 的物体 A,置于光滑水平桌面上。现通过一质量为 m、半径为 R 的定滑轮 B(可视为匀质圆 盘)用细绳连接另一质量为 m2 的物体 C,设细绳不可伸长,且与滑轮间无相对滑动,求系统的 振动角频率。 13-6 分析 这是一个由弹簧、物体 A、C 和滑轮 B 组成的简谐运动系统。 求解系统的振动频率 可采用两种方法。 (1)从受力分析着手。 如图 13-6(b)所示,设系统处于平衡状态时,与 物体 A 相连的弹簧一端所在位置为坐标原点 O,此时弹簧已伸长 x0,且 kx0 = m2 g 。 当弹簧沿 Ox 轴正向从原点 O 伸长 x 时,分析物体 A、C 及滑轮 B 的受力情况,并分别列出它们的动力学方程, 可解得系统作简谐运动的微分方程。 (2)从系统机械能守恒着手。 列出系统机械能守恒方程, 然后求得系统作简谐运动的微分方程。 解 1 在图 13-6(b)的状态下,各物体受力如图 13-6(c)所示。 其中 F k(x x )i = − + 0 。 考虑到绳子不可伸长,对物体 A、B、C 分别列方程,有 2 2 1 0 1 ( ) dt d x FT − k x + x = m (1) 2 2 2 2 2 dt d x m g − FT = m (2) 2 2 2 1 2 1 ( ) dt d x FT − FT R = J = mR (3) kx0 = m2 g (4) 方程(3)中用到了 FT FT ' FT FT ' J mR / 2 a / R 2 1 = 1 、 2 = 2 、 = 、及 = 。 联立式(l)-式(4) 可得

dx 网+隔+2-0 则系统氟动的角频事为 四三√km+网3+m/2) 解2取整个量动装置和地球为研究系统,国没有外力和非保守内力作功,系统机械能守恒。 设物体平衡时为初始代志,物体向右偏移距离X(此时速度为对?·如速度为)为末状老,则 由机板能守恒定律,有 现+广公2+红+ 2 在列出上述方程时应注意势能《重力势能和弹性势伦》罗点的选取。为运算方便,选初始状古 下物体C所在位置为重力势能零点:弹簧原长时为弹性势能的零点。将上述方程对时间求导得 0=-偶gT+偶 +周 +a +制x+离月 h 将J-m/2.成-h/山-dx/r和Lg=k代人上式,可得 式(6》与式(5)相同,表明再种解法结果一致, 17-7一成置在水平桌面上的弹簧最子。佩幅A-20×102m周用T05054当0时,(1)物体 在正方向端点:(2)物体在平衡位置向负方向国动:(3)物体在3x-10×10m处,向负方向运 动:(4)物体在x■-1,0×102m处,向正方向运动。求以上各种情况的运动方程。 13-7 分析在板幅A和周期T已知的条件下,确定初相中是求解简语运动方程的关键。初相的确定通 常有两种方法。(1)解析法由振动方程出发,根据初始条件,即”0时,x无和v三,米 确定e值。(2)旋转失量法:如图13-7《a)所示,将质点P在0轴上据动的橱如位置x 和速度的方向与旋转失量图相对应米确定单,旋转天量法比较直观、方便,在分析中常采用: 解由圆给条件知A=20x10团,可一2x/T=4西,而初相e可采用分析中的两种不同 方法来观。 解法:根据简话超动方程x■AG+),当t■0时有玉=As9,0==A国sn停。 当
0 1 2 / 2 2 2 = + + + x m m m k dt d x 则系统振动的角频率为 /( / 2) = k m1 + m2 + m 解 2 取整个振动装置和地球为研究系统,因没有外力和非保守内力作功,系统机械能守恒。 设物体平衡时为初始状态,物体向右偏移距离 X(此时速度为对 v 、加速度为 a)为末状态,则 由机械能守恒定律,有 2 0 2 2 2 2 2 1 2 0 ( ) 2 1 2 1 2 1 2 1 2 1 k x = −m gx + m v + m v + J + k x + x 在列出上述方程时应注意势能(重力势能和弹性势能)零点的选取。 为运算方便,选初始状态 下物体 C 所在位置为重力势能零点;弹簧原长时为弹性势能的零点。 将上述方程对时间求导得 2 2 1 2 0 0 k(x x ) dt dv J dt dv m v dt dv = −m gv + m v + + + + 将 2 0 2 2 2 J = mR / 2、R = v、dv / dt = d x / dt 和m g = k x 代人上式,可得 0 1 2 / 2 2 2 = + + + x m m m k dt d x 式(6)与式(5)相同,表明两种解法结果一致。 17-7 一放置在水平桌面上的弹簧振子,振幅 A=2.0×10-2m,周期 T=0.50s。当 t=0 时,(1)物体 在正方向端点;(2)物体在平衡位置向负方向运动;(3)物体在..x=1.0×10-2m 处,向负方向运 动;(4)物体在..x= -1.0×10-2m 处,向正方向运动。求以上各种情况的运动方程。 13-7 分析 在振幅 A 和周期 T 已知的条件下,确定初相中是求解简谐运动方程的关键。初相的确定通 常有两种方法。(1)解析法:由振动方程出发,根据初始条件,即 t= 0 时, x= xo 和 0 v = v 来 确定 值。 (2)旋转矢量法:如图 13-7(a)所示,将质点 P 在 Ox 轴上振动的初始位置 x0 和速度 v0 的方向与旋转矢量图相对应来确定 。 旋转矢量法比较直观、方便,在分析中常采用。 解 由题给条件知 A m 2 2.0 10− = , 1 2 / 4 − = T = s ,而初相 可采用分析中的两种不同 方法来求。 解析法:根据简谐运动方程 x = Acos(t +) ,当 t=0 时有 x0 = Acos ,v0 = −A sin 。 当

《1)无=4时e0s%=1.则g=0 (2)名=时,04=0则码=±经因。<0取码- 《3)无=10x10w时.o0s%=05则%=号因%<0取码=子 名-10x0时5题=号6a取,- 3 旋转矢量法:分别面出四个不同初始找态的旋转美量图,如图13-7()所示,它们所对应 的初相分测为%-0,%-夏/2,停-g/3,4=4红/3: 丽幅A,角频率四,初相口均确定后。则各相应状志下的运动方程为 41)x=(2.0×10w0os4g (2)xy (3)-20x0mco4ag+ (4)=xm)co 138有一弹簧,当其下端挂一质量为曲的物体时,伸长量为9.8×102m。若使物体上下振动, 且规定向下为正方向.《1)0时,物体在平衡位置上方80×10■处,由静止开始向下运动, 象运动方程。(2)0时。物体在平衡位置并以060m小的速度向上运动,乘运动方程, b 13-8 分析求运动方程。也就是要确定握动的三个特征物理量A、⑧,和?:其中量动的角频率是 山弹簧暴予系统的国有性质(振子质量■及弹簧劲度系数k》浇定的。即心■、√/m,可根据物 体受力平衡时弹簧的伸长来计算:探幅A和初相需要复据初始条件确定。 解物体受力平衡时,弹性力F与重力P的大小相等,即P。而此时弹簧的伸长量 W=98×10广刚。则弹簧的动度系数k=F/山=四/W。系统作简著运动的角频率为 a=1w-g1-10s (1)设系绕平衡时,物体所在处为坐标眼点,向下为夏轴正向。由初始条件10时, 。=8.0x0m,,=0可得耀幅4-√2+(0/了=80x10周:应用旋转矢量法可确定
(1) x0 = A时,cos1 =1,则1 = 0; (2) 时, ,则 ,因 ,取 ; 2 0 2 0 cos 2 0 2 0 2 x = A = = v = (3) 时, ,则 ,因 ,取 ; 3 0 3 1.0 10 cos 3 0.5 3 0 3 2 0 = = = = − x m v (4) 时, ,则 ,因 ,取 ; 3 4 0 3 1.0 10 cos 4 0.5 4 0 4 2 0 = − = − = = − x m v 旋转矢量法:分别画出四个不同初始状态的旋转关量图,如图 13-7(b)所示,它们所对应 的初相分别为 1 = 0,1 = / 2 ,1 = / 3,1 = 4 / 3。 振幅 A、角频率 、初相 均确定后,则各相应状态下的运动方程为 (1) x (2.0 10 m) cos(4 s )t −2 −1 = (2) ] 2 (2.0 10 )cos[(4 ) 2 1 = + − − x m s t (3) ] 3 (2.0 10 )cos[(4 ) 2 1 = + − − x m s t (4) ] 3 4 (2.0 10 ) cos[(4 ) 2 1 = + − − x m s t 13-8 有一弹簧,当其下端挂一质量为 m 的物体时,伸长量为 9.8×10-2m。若使物体上下振动, 且规定向下为正方向。(1)t=0 时,物体在平衡位置上方 8.0×10-2m 处,由静止开始向下运动, 求运动方程。(2)t=0 时,物体在平衡位置并以 0.60m/s 的速度向上运动,求运动方程。 13-8 分析 求运动方程,也就是要确定振动的三个特征物理量 A、 ,和 。 其中振动的角频率是 由弹簧振子系统的固有性质(振子质量 m 及弹簧劲度系数 k)决定的,即 = k /m ,可根据物 体受力平衡时弹簧的伸长来计算;振幅 A 和初相 需要根据初始条件确定。 解 物体受力平衡时,弹性力 F 与重力 P 的大小相等,即 F=mg。 而此时弹簧的伸长量 l m 2 9.8 10− = 。 则弹簧的劲度系数 k = F /l = mg /l 。 系统作简谐运动的角频率为 1 / / 10 − = k m = g l = s (1)设系统平衡时,物体所在处为坐标原点,向下为 x 轴正向。 由初始条件 t=0 时, x m 2 10 8.0 10 − = , v10 = 0 可得振幅 A x v m 2 2 10 10 2 ( / ) 8.0 10− = + == ;应用旋转矢量法可确定
初相级=。[图13-8(a)]。则运动方程为 马,-(80×0m)cosk0:r+r] (2》t0时,x多=0,=0.6m手1,同理可得4=√”+n/=60x103m: %-/2:[图13-8(h)],则运动方程为 无=(6.0×109m0osk10sr+0.5xl 159某银动质点的x-1曲线如图所示,试求:《1)运动方程:(2)点P对应的相位:(3)到达 点P相应位置所需要的时间, 4¥ 0.10 0.05 4.0 13-9 分析由已知运动方程西振诗由线和由振动曲线求运功方程是佩功中常见的两类利题。本题藏 是要通过x1图线确定丽动的三个特征量量人,#,和风,从而写出运动方程。由线最大额值 即为扳幅:而。,通常可通过旋转矢量法或解析法解出,一毅采用鬓转矢量法比校方便 解(1)质点振动振氢A=0.10,而由服功曲线可面出1=0和=48时能转矢量,如图 13-9(b)所示。 由图可见初相风=-好/到暖风=5知/),雨由,-%)上乃+为得 世=5r/24,则运动方程为 x=0.10网e0 票-列 (2)图14-9(a》中点P的位置是质点从A/2处运 动到正向的端点处。应的旋转关量图如图13-10(C) 所示。当初相取风=一/3时,点P的相位为 ,=+例,-0=0(如果初相取%=5好/3,则点P f=0 相应的相位应表示为。=+0,-0)=2灯). (e) (3)由装特关量图可得%。-0)-乃期(,=16 130在一块平板下装有弹簧。平板上故一质景为1处g的重物。现使平板沿经直方向做上下 简话运动,属期为030s,振幅为2.0×10m。求:《1)平板到最低点时,重物对平板的作用力: (2)若顿率不变。则平板以多大的据幅据时时,重物金跳离平板:(3)若探解不变,则平版以 多大的顿率振动时,重物会洗离平板?
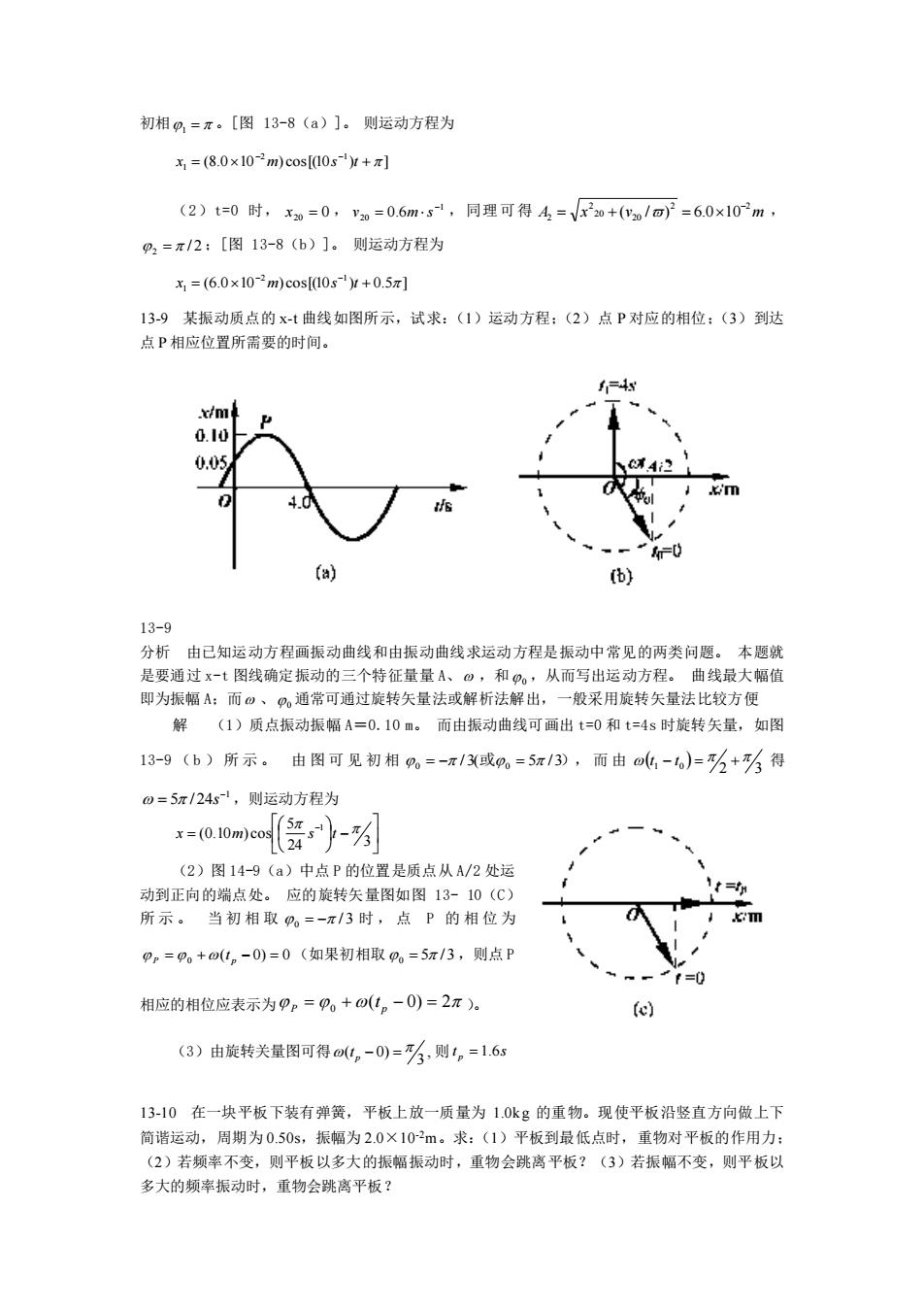
初相 1 = 。[图 13-8(a)]。 则运动方程为 (8.0 10 ) cos[(10 ) ] 2 1 1 = + − − x m s t (2)t=0 时, x20 = 0 , 1 20 0.6 − v = m s ,同理可得 A x v m 2 2 20 20 2 2 ( / ) 6.0 10− = + = , 2 = / 2 ;[图 13-8(b)]。 则运动方程为 (6.0 10 ) cos[(10 ) 0.5 ] 2 1 1 = + − − x m s t 13-9 某振动质点的 x-t 曲线如图所示,试求:(1)运动方程;(2)点 P 对应的相位;(3)到达 点 P 相应位置所需要的时间。 13-9 分析 由已知运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。 本题就 是要通过 x-t 图线确定振动的三个特征量量 A、 ,和 0 ,从而写出运动方程。 曲线最大幅值 即为振幅 A;而 、 0 通常可通过旋转矢量法或解析法解出,一般采用旋转矢量法比较方便 解 (1)质点振动振幅 A=0.10 m。 而由振动曲线可画出 t=0 和 t=4s 时旋转矢量,如图 13-9 (b )所示。 由图可见初相 0 = − / 3(或 0 = 5 / 3) ,而由 ( ) 2 3 1 0 t − t = + 得 1 5 / 24 − = s ,则运动方程为 − = − 3 24 5 (0.10 ) cos 1 x m s t (2)图 14-9(a)中点 P 的位置是质点从 A/2 处运 动到正向的端点处。 应的旋转矢量图如图 13- 10(C) 所示。 当初相取 0 = − / 3 时,点 P 的相位为 P = 0 +(t p − 0) = 0 (如果初相取 0 = 5 /3 ,则点 P 相应的相位应表示为 P = 0 +(t p − 0) = 2 )。 (3)由旋转关量图可得 , 3 ( − 0) = p t 则 t s p = 1.6 13-10 在一块平板下装有弹簧,平板上放一质量为 1.0kg 的重物。现使平板沿竖直方向做上下 简谐运动,周期为 0.50s,振幅为 2.0×10-2m。求:(1)平板到最低点时,重物对平板的作用力; (2)若频率不变,则平板以多大的振幅振动时,重物会跳离平板?(3)若振幅不变,则平板以 多大的频率振动时,重物会跳离平板?

777777777 13-10 分析按题意作示意图13-10,物体在平衡位置附近随板作简谐运动,其侧受重力P和板支特 力下,作用,下是一个变力。按华顿定律,有 F-n-F-my (1) h 由于物体是随酸一起作简话运动,因面有:一 =-4w2c0w+),则式(1)可改写为 Fy三g+限42 costan+) (2) (1)根那版运动的位置,确定此刻氟动的相位解+拿。由式(2)可求版与物体之间的作用 力。 (2)由式(2)可知支持力P,的值与握幅A,角懒率台和相位+单有关。在振动过程中, 当+?-x时F,最小,而重物怡好跳离平版的条件为F=0,因此由式(2)可分别求出重物跳 离平板所萄的频率或振幅。 解(1)由分析可知,重物在最低点时,相位+单=0。物体受版的支特力为 F=限+m42=s+2行=2.96N 重物对木块的作用力F,'与卡大小相等,方向相反。 (2)当规率不变时,设振幅变为看。鼠据分析中所述,将F,-0及+P一常代入分析中 式(2,可得 术-g/mg2-gf2/4r2=6.2×0w 《3)当振幅不变时,设频率变为。同样将F=0及代入分析中式(2入可得 兰名属m32业 13-11一物体沿x轴做简谐运动,氟幅为0.06m,周期为2.0s,当t0时位移为0.03m,且向x 轴正方向运动。求:(1)0.5s时,物体的位移、速度和如速度:(2)物体从x=003处向x 轴负向阔动开始。到平衡位置,至少需要多少时间?
13-10 分析 按题意作示意图 13-10。 物体在平衡位置附近随板作简谐运动,其间受重力 P 和板支持 力 FN 作用,FN 是一个变力。 按牛顿定律,有 2 2 dt d y F = mg − FN = m (l) 由于物体是随板一起作简谐运动,因而有 cos( ) 2 2 2 = = −A t + dt d y a ,则式(l)可改写为 cos( ) 2 FN = mg + mA t + (2) (1)根据板运动的位置,确定此刻振动的相位 t + ,由式(2)可求板与物体之间的作用 力。 (2)由式(2)可知支持力 FN 的值与振幅 A、角频率 和相位 t + 有关。 在振动过程中, 当 t + = 时 FN 最小。而重物恰好跳离平板的条件为 FN=0,因此由式(2)可分别求出重物跳 离平板所需的频率或振幅。 解 (l)由分析可知,重物在最低点时,相位 t + = 0 ,物体受板的支持力为 N T FN mg mA mg mA ) 12.96 2( 2 2 = + = + = 重物对木块的作用力 ' FN 与 FN 大小相等,方向相反。 (2)当频率不变时,设振幅变为 A' 。 根据分析中所述,将 FN=0 及 t + = 代入分析中 式(2),可得 A mg m gT m 2 2 2 2 / / 4 6.2 10 − = = = (3)当振幅不变时,设频率变为 ' 。 同样将 FN=0 及代入分析中式(2),可得 v mg /mA 3.52Hz 2 1 2 = = = 13-11 一物体沿 x 轴做简谐运动,振幅为 0.06m,周期为 2.0s,当 t=0 时位移为 0.03m,且向 x 轴正方向运动。求:(1)t=0.5s 时,物体的位移、速度和加速度;(2)物体从 x= -0.03m 处向 x 轴负向运动开始,到平衡位置,至少需要多少时间?

13-11 分析已如蹈动方程即可求物体的位移、速度、如速度。因此,写出运动方程是本题的关键。其 方法可参见题13了。至于频点从x=-0.03■运动到夏=0处所雷的最妇时间,仍可果用解新法 或旋特矢量法求解。 (a) b 解(1)由意知A0.06、=2x/T=由旋转失量图13-11《a)可确定初相侧 动方程为 x-06 m)co-列 当1=0.5s时质点的位移,速度,加速度分刚为 x-(0.06m)cod-0.052 v=时=-006msm(乃-=004m a=产仙=-006rm)e05-=-0,513m (2)质点从x-0.3■运动到甲衡位置的过程中。旋转关量从图13-11(仙)中的位置■ 转至位置N,矢量转过的角度(即相位差》Ag=5x/6。该过程所雷时间为 M=%=083 13-2两质点数通频礼、月振幅的简清运动。第一个质点的运动方程为=A何+)。当 第一个质点自雨动正方向回到平衡位置时,第二个额点恰在振动正方向的编点,试用能转矢量用 表示它们,并求第二个颜点的运动方程及它《1的相位差, 13-12 解图13-12为两质点在特定时刻1的能转矢量图,表示第一个质点据动的能转实量:0N 表示第二个质点振时的能转矢量。可见第一个板点振动的相悦比第二个质点超前开/2,即它们
13-11 分析 已知运动方程即可求物体的位移、速度、加速度。 因此,写出运动方程是本题的关键。 其 方法可参见题 13-7。 至于质点从 x=-0.03 m 运动到 x=0 处所需的最短时间,仍可采用解析法 或旋转矢量法求解。 解 (1)由题意知 A=0.06m、 1 2 / − = T = s 由旋转矢量图 13-11(a)可确定初相则振 动方程为 ( ) 3 (0.06 )cos x = m s −1 t − 当 t=0.5s 时质点的位移、速度、加速度分别为 ( ) 2 2 2 2 2 1 1 ) 0.513 2 3 (0.06 )cos( ) 0.094 2 3 (0.06 )sin( 0.052 2 3 (0.06 )cos − − − − = = − − = − = = − − = = − = a d x dt m s m s v dx dt m s m s x m (2)质点从 x=-0.03 m 运动到平衡位置的过程中,旋转关量从图 13-11(b)中的位置 M 转至位置 N,矢量转过的角度(即相位差) = 5 /6 。该过程所需时间为 t = 0.833s = 13-12 两质点做通频率、同振幅的简谐运动。第一个质点的运动方程为 cos( ) x1 = A t + ,当 第一个质点自振动正方向回到平衡位置时,第二个质点恰在振动正方向的端点。试用旋转矢量图 表示它们,并求第二个质点的运动方程及它们的相位差。 13-12 解 图 13-12 为两质点在特定时刻 t 的旋转矢量图,OM 表示第一个质点振动的旋转矢量;ON 表示第二个质点振动的旋转矢量。 可见第一个质点振动的相位比第二个质点超前 / 2 ,即它们

的相位差△x/2。第二个顺点的运动方程应为 为=Ae0s+-为 13-13有一单摆,长为10m,最大摆角为5,如图所示。(1)求摆的角期率和周期:(2)设开 始时摆角最大,试写出此单理的运动方程:(3)当摆角为3时的角速度和摆球的线速度时多少? ∠LL∠L 13-13 分析单摆在摆角较小时(8<5)的摆动。其角量8与时 间的关系可表示为简请运动方程8-日。.c0s+),其中 角顿率谷仍由该系统的性质(重力如速度g和绳长!)决定, 10m ,。初相停与摆角8,质点的角速度与旋转矢量的 角速度(角频率)均是不月的物理慨念,必注意区分: 解(1)单层角频率及周期分别为 m-7-313T.2%-20 《2》由=0时0=8。一可得振功初相g=0,则以角量表示的简塔运动方程为 c0s(3.13r"y 3)摆角为3时。有e0s+)= 9%=06.则这时颜点的角速度为 dod=-0srfo+)=-0-cos (o+) =0890=-0218s 线速度的大小为 v=例d域=0218w 付论质点的规速度和角速度也可通过机械能守恒定律乘解,但结果会有极微小的差别。这 是国为在导出筒游运动方程时曾取s00,所以,单摆的简请阔动方程仅在8较小时成立。 1314为了测月球表面的重力加建度,字航员将地面上的秒摆(周期为2.00s》拿到月球上去, 如测得周期为4.90s,地球表面得重力如速度为9.80m公,则月球表面得重力扣速度是多少? 13-14 解由单探的周期公式T=2xWg可知gCVT2,故有u/g:-TT,,则月球的重力加 速度为 8v=(T:/TuFgr =163m-s 155一均匀等边三角形薄板,衢量为m,高度为h。如图所示。当其绕AB边(与水平轴线重 合》转动时,试证其做微小振动的周期为T=2x√/2g
的相位差 / 2 。第二个质点的运动方程应为 ) 2 cos( 2 x = A t + − 13-13 有一单摆,长为 1.0m,最大摆角为 5 0,如图所示。(1)求摆的角频率和周期;(2)设开 始时摆角最大,试写出此单摆的运动方程;(3)当摆角为 3 0 时的角速度和摆球的线速度时多少? 13-13 分析 单摆在摆角较小时( 0 5 )的摆动,其角量 与时 间的关系可表示为简谐运动方程 cos( ) = max t + ,其中 角频率 仍由该系统的性质(重力加速度 g 和绳长 l )决定, 即 l g = 。初相 与摆角 ,质点的角速度与旋转矢量的 角速度(角频率)均是不同的物理概念,必须注意区分。 解 (1)单摆角频率及周期分别为 s T s l g 2.01 2 3.13 ; 1 = = = = − (2)由 t=0 时 0 = m ax = 5 可得振动初相 = 0 ,则以角量表示的简谐运动方程为 cos(3.13s )t 36 −1 = (3)摆角为 3 0 时,有 cos( ) 0.6 max + = = t ,则这时质点的角速度为 1 max 2 max max 0.8 0.218 sin( ) 1 cos ( ) − = − = − = − + = − − + s t t dt d 线速度的大小为 1 0.218 − v = l d dt = ms 讨论质点的线速度和角速度也可通过机械能守恒定律求解,但结果会有极微小的差别。 这 是因为在导出简谐运动方程时曾取 sin ,所以,单摆的简谐运动方程仅在 较小时成立。 13-14 为了测月球表面的重力加速度,宇航员将地面上的秒摆(周期为 2.00s)拿到月球上去, 如测得周期为 4.90s,地球表面得重力加速度为 9.80m/s2,则月球表面得重力加速度是多少? 13-14 解 由单摆的周期公式 T = 2 l g 可知 2 g 1 T ,故有 2 2 gM gE = TE TM ,则月球的重力加 速度为 ( ) 2 2 1.63 − g = T T g = ms M E M E 13-15 一均匀等边三角形薄板,质量为 m,高度为 h,如图所示。当其绕 AB 边(与水平轴线重 合)转动时,试证其做微小振动的周期为 T = 2 h / 2g