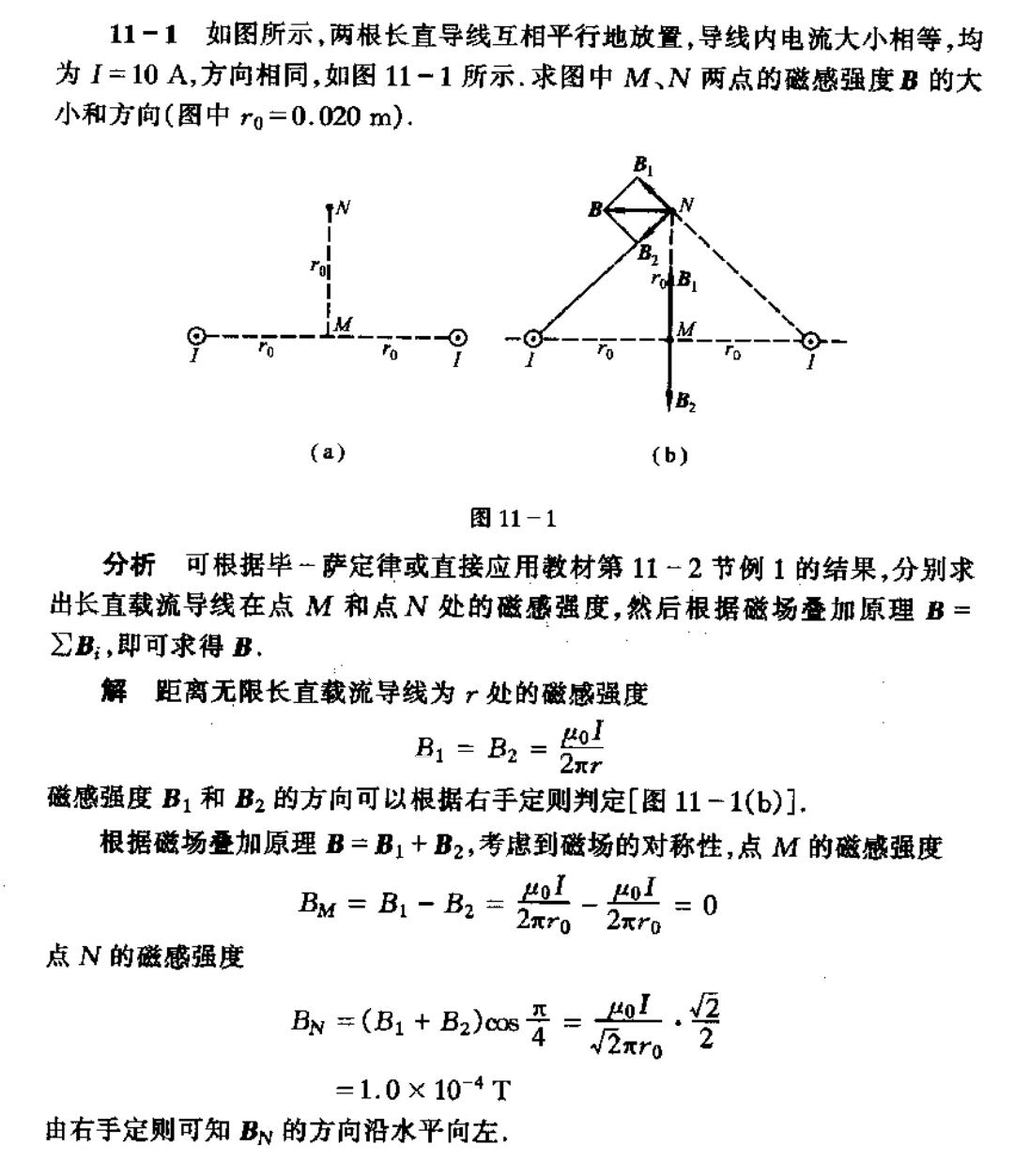
11-1如图所示,两根长直导线互相平行地放置,导线内电流大小相等,均 为I=10A,方向相同,如图11-1所示.求图中M、N两点的磁感强度B的大 小和方向(图中r0=0.020m). (a】 b 图11-1 分析可根据毕一萨定律或直接应用教材第11~2节例1的结果,分别求 出长直载流导线在点M和点N处的磁感强度,然后根据磁场叠加原理B= ∑B:,即可求得B. 解距离无限长直载流导线为?处的微感强度 A== 磁感强度B1和B2的方向可以根据右手定则判定[图11-1(b)]. 根据磁场叠加原理B=B1+B2,考虑到磁场的对称性,点M的磁感强度 A=A-=兴-=0 点N的磁感强度 =(B1+B2)os香=2x0艺 L.2 =1.0×104T 由右手定则可知BN的方向沿水平向左
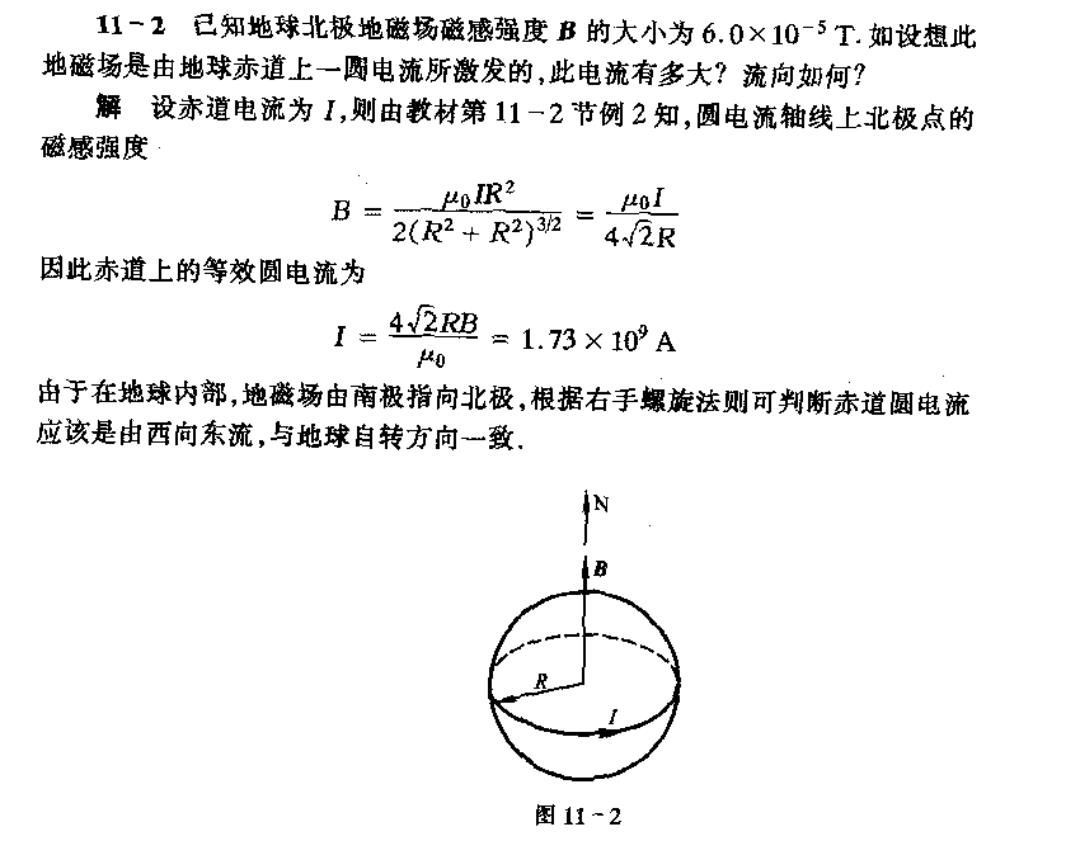
11一2已知地球北极地磁扬磁感强度B的大小为6.0×105T.如设想此 地磁场是由地球赤道上一园电流所激发的,此电流有多大?流向如何? 解设赤道电流为1,则由教材第11一2节例2知,圆电流轴线上北极点的 磁感强度 B=20=鼎 0R2 因此赤道上的等效圆电流为 【=42=1.73×10A 40 由于在地球内部,地盛场由南极指向北极,根据右手螺旋法则可判断赤道圆电流 应该是由西向东流,与地球自转方向一致、 图11~2

11一3如图所示,有两根导线沿半径方向接触铁环的4、6两点,并与很远 处的电源相接。求环心O的磁感强度. 分析根据叠如原理,点O的磁惑强度可视作由、、石三段直线以及 b、aa6两段圆孤电流共同激发.由于电源距环较远,8/=0,而、石两段直线 的延长线通过点O,由于Idl×r=0,由毕-萨定律知Be=Ba=0.流过圆弧的 电流】1、12的方向如图所示,两圆弧在点O激发的磁场分别为 品=华:8=9 4πr2 其中1、l2分别是圆孤acb、a@b的弧长,由于导线电阻R与孤长1成正比,而圆 弧acb、adb又构成并联电路,故有 1l1=I22 将B1、B2養加可得点O的磁感强度B, 解由上述分析可知,点O的合磁感强度 B=B1-B2=0g-9=0 4πr9 4π扩4 图11-3
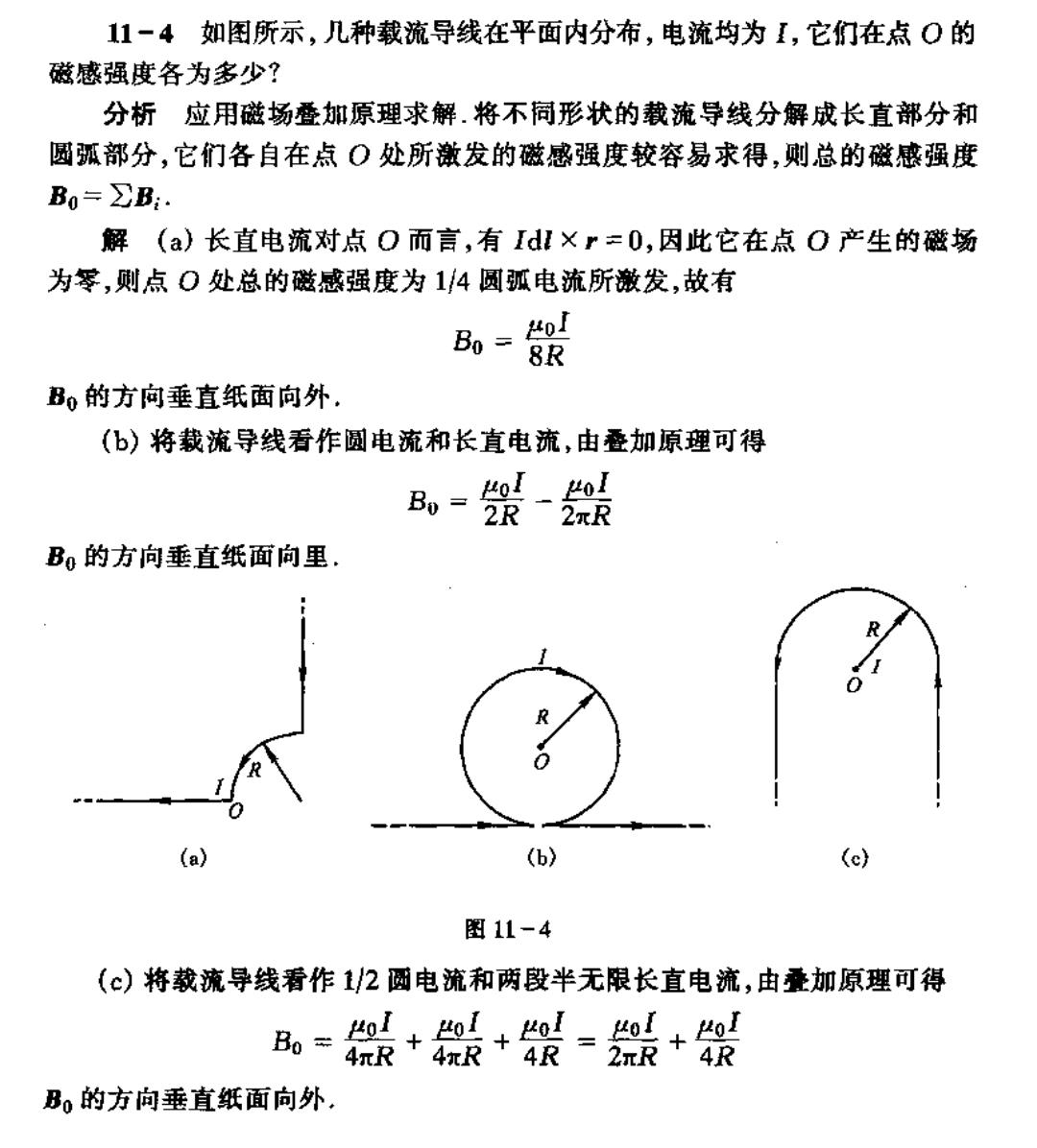
11一4如图所示,几种载流导线在平面内分布,电流均为【,它们在点O的 磁感强度各为多少? 分析应用磁场叠加原理求解.将不同形状的载流导线分解成长直部分和 圆弧部分,它们各自在点O处所激发的磁感强度较容易求得,则总的磁感强度 B0=2B: 解(a)长直电流对点O而言,有Id!×r=0,因此它在点O产生的磁场 为零,则点0处总的磁感强度为14圆弧电流所澈发,散有 8,=架 B。的方向垂直纸面向外. (b)将裁流导线看作圆电流和长直电流,由叠加原理可得 品祭黑 B。的方向垂直纸面向里. ( (b) Le) 图11-4 (©)将载流导线看作12圆电流和两段半无限长直电流,由叠加原理可得 品+装+欲=+祭 B,的方向垂直纸面向外」
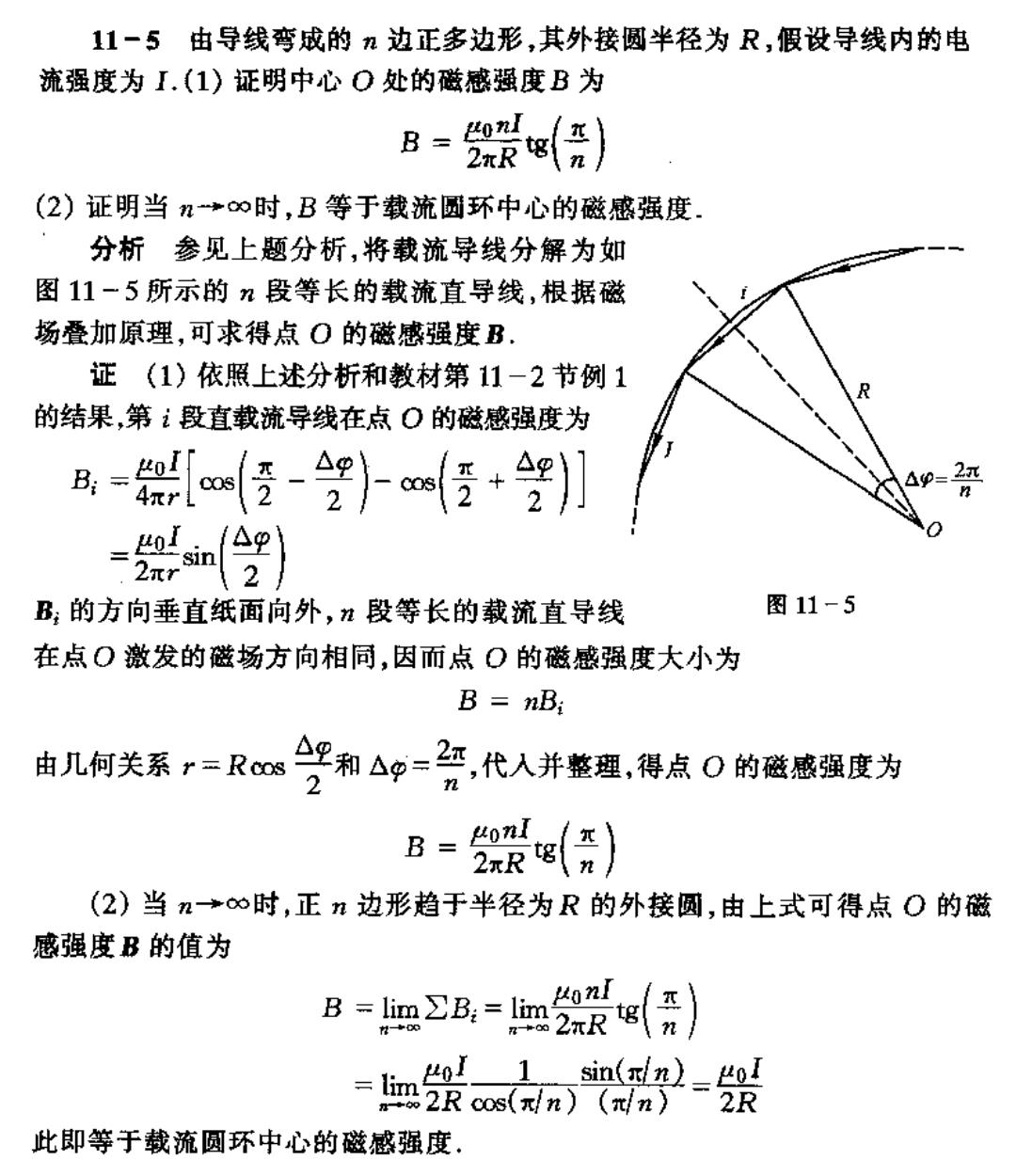
11一5由导线弯城的n边正多边形,其外接圆半径为R,假设导线内的电 流强度为I.(1)证明中心O处的磁感强度B为 B=%装】 (2)证明当n+∞时,B等于载流圆环中心的磁感强度 分析参见上题分析,将载流导线分解为如 图11-5所示的n段等长的载流直导线,根据磁 场叠加原理,可求得点O的磁感强度B 证(1)依照上述分析和教材第11-2节例】 的结果,第i段直载流导线在点。的磁感强度为 4=器m3-3+】 =%m) B:的方向垂直纸面向外,n段等长的载流直导线 图11-5 在点O激发的磁场方向相同,因而点。的磁感强度大小为 B=nB. 由儿何关系r=Rcos 号和△p-织,代入并整理,得点O的磁感强度为 B=2() (2)当n→∞时,正n边形趋于半径为R的外接圆,由上式可得点0的磁 感强度B的值为 B=趣2B,=2xRg( =张n-祭 此即等于载流圆环中心的磁感强度
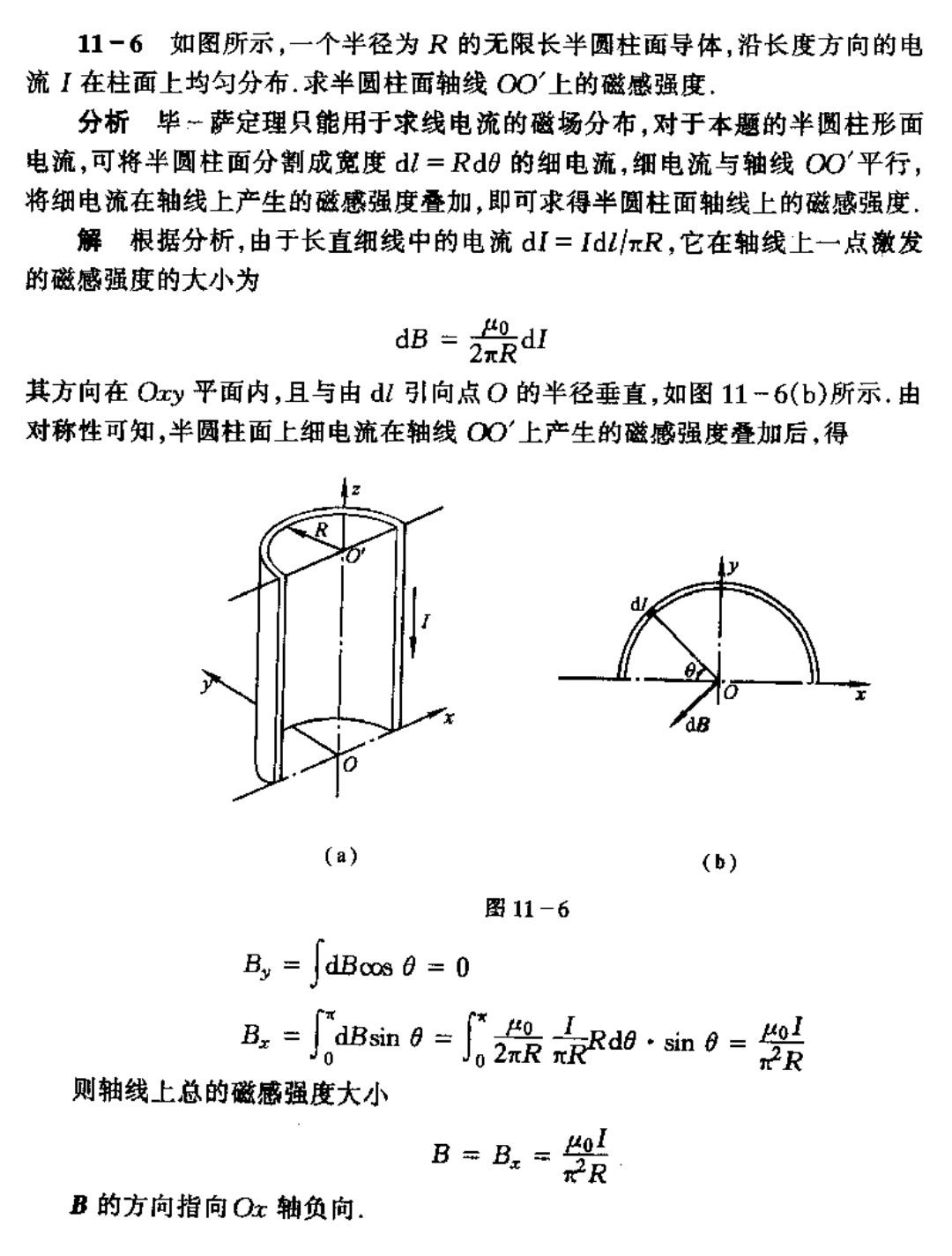
11-6如图所示,一个半径为R的无限长半圆柱面导体,沿长度方向的电 流【在柱面上均匀分布.求半团柱面轴线O0上的磁感强度 分析毕一萨定理只能用于求线电流的磁场分布,对于本题的半圆柱形面 电流,可将半圆柱面分割成宽度dl=R0的细电流,细电流与轴线OO平行 将细电流在轴线上产生的磁惑强度叠加,即可求得半圆柱面轴线上的磁感强度 解根据分析,由于长直细线中的电流dI=IdL/πR,它在轴线上一点澈发 的磁感强度的大小为 dB=景dl 其方向在Oxy平面内,且与由引向点0的半径垂直,如图11-6(b)所示.由 对称性可知,半圆柱面上细电流在轴线OO上产生的磁感强度叠加后,得 (a (b) 图11-6 B,=dBco8日=0 B,=aBs血0=02景kd0·m9= 则轴线上总的磁感强度大小 B=B=贺 B的方向指向Ox轴负向

11一7如图所示,半径为R的木球上绕有密集的细导线,线圈平面彼此平 行,且以单层线图覆盖住半个球面,设线圈的总匝数为N,通过线圈的电流为I. 求球心O处的磁感强度. (a) (b) 图11-7 分析作截面Oxy与线圈正交,由于导线单层均匀覆盖在半球面上(图11 -7),沿圆周单位长度的线圈匝数为N/(2xR现将半球面分剂为无数薄圆 盘片,则任一薄圆盘片均可等效为一个圆电流,由于每个薄圆盘片上的电流在球 心O产生的磁感强度方向一致,则球心O的磁感强度为 B=dB 解 根据分析,任一薄圆盘片中的电流为 dI IdN 2N R ·Rd0· 该圆电流在球心O处激发的磁场,由教材第11-2节例2可得,为 dB =Ko y2 2(x2 3y2)2d/ 球心O处总的磁感强度B为 r2 (x2 由图11-7(b)可知x=Rco80;y=Rsin9.将它们代人上式,得 B=。 Rsin 0d0=LoNI 2 goNI 4R 磁感强度B的方向由电流的流向根据右手定则确定
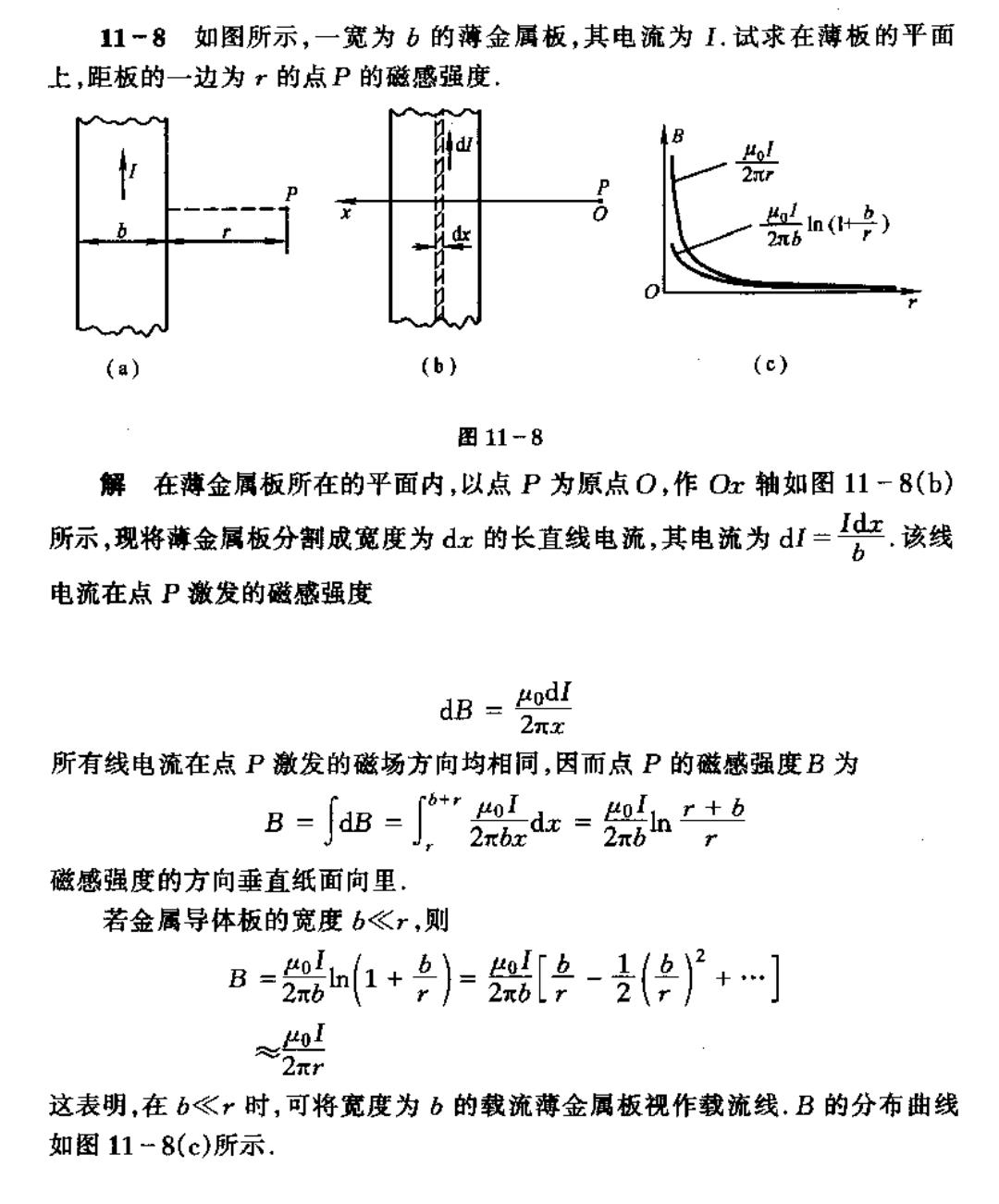
11-8如图所示,一宽为b的薄金属板,其电流为I.试求在薄板的平面 上,距板的一边为r的点P的磁感强度, (b) (e) 图11-8 解 在薄金属板所在的平面内,以点P为原点O,作Ox轴如图11-8(b)》 所示,现将薄金属板分剂成宽度为正的长直线电流,其电流为d山=化该线 电流在点P激发的磁感强度 dB eodI 2πx 所有线电流在点P激发的磁场方向均相同,因而点P的磁感强度B为 磁感强度的方向垂直纸面向里 若金属导体板的宽度b《r,则 B-+)-器2-+…] 2πr 这表明,在b《r时,可将宽度为b的载流薄金属板视作载流线.B的分布曲线 如图11-8(c)所示

11-9实验室中常用所谓的亥姆霍兹线圈在局部区域内获得一近似均匀的 磁场,其装置简图如图11-9()所示.一对完全相同、彼此平行的线圈,它们的半径 均为R,通过的电流均为1,且两线圈中电流的流向相同.试证:当两线圈中心之间 的距离d等于线圈的半径R时,在两线圈中心连线的中点附近区域,磁场可看成 是均匀磁场.(提示:如以两线圈中心连线的中点为坐标原点O,两线圈中心连线 为x轴则中点附近的陆场可雪成是均匀磁场的条件为盟=0程-0,) (a) (b) 图11-9 分析设磁感强度在Ox轴线上的分布为B(x)(可由两个圆电流线圈在轴 线上磁杨的羹加而得),如在轴线上某点处盟-0,这表明在该点附近的磁感强 度有三种可能,即有极大值(碧0)或均匀(盟=0)·据此 可得获得均匀磁杨的条件①】 证取两线圈中心连线的中点为坐标原点O,两线圈中心轴线为x轴,在 x轴上任一点的磁感强度 B= 40R2 BoIR2 2IR2+(d2-xP亚+2[R2+(a2+z]m 则当 dB(z)=LoI 3(d2-x】 3(d2+x】 dr 2R2+(a2-xR2+(a2+y=0 .3y引04a+4品-0 dx 时,磁感强度在该点附近小区域内是均匀的,该小区城的磁场为均匀场, 由 dB(z=0,解得x=0 dx 由 PB(z) dx =0,解得d=R x=0 这表明在d=R时,中点(x=0)附近区域的磁场可视为均匀磁场
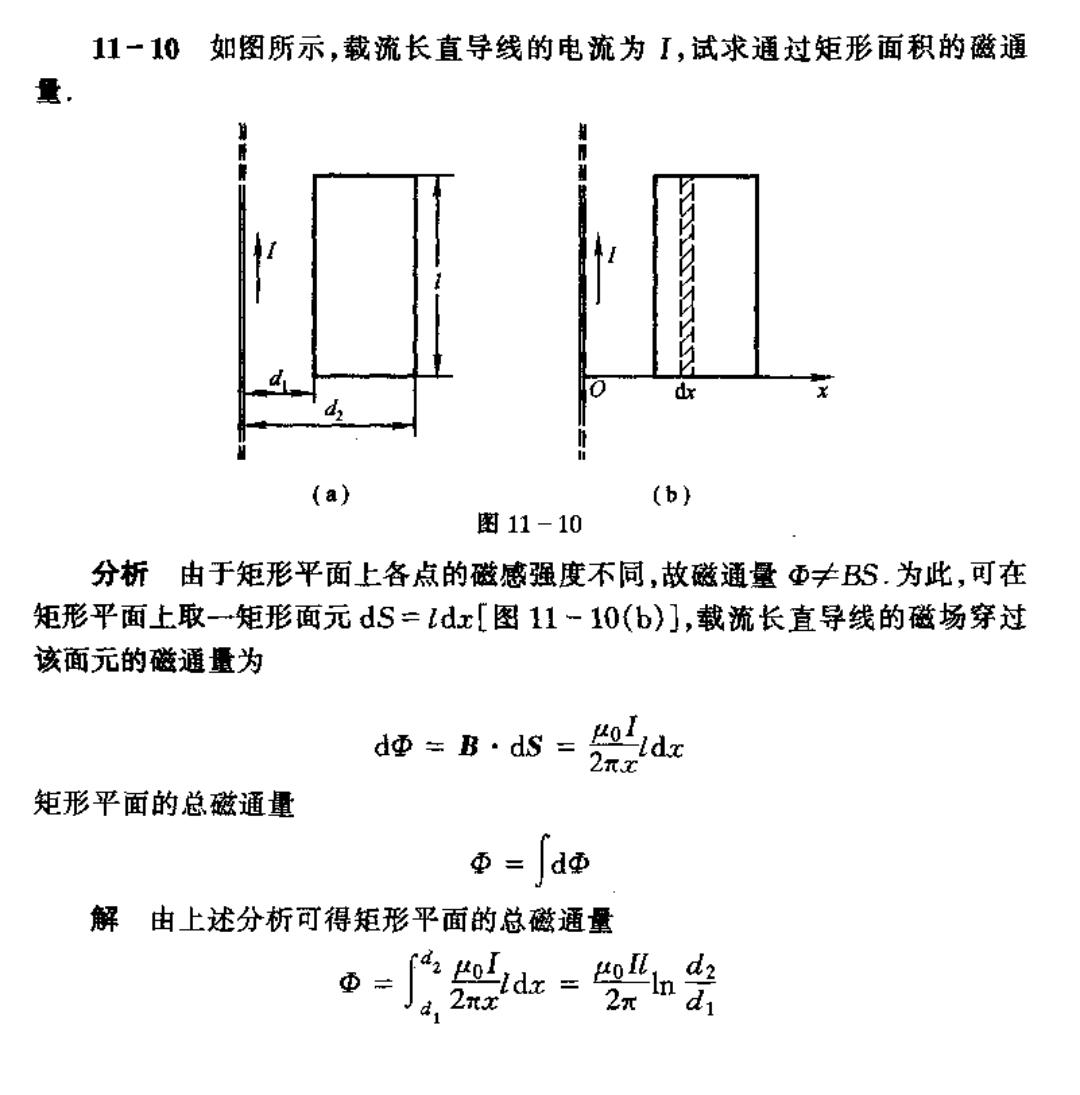
11一10如图所示,载流长直导线的电流为I,试求通过矩形面积的磁通 (a) (b) 图11-10 分析由于矩形平面上各点的磁感强度不同,故磁通量Φ≠BS.为此,可在 矩形平面上取一矩形面元dS=dx[图11-10(b)],载流长直导线的磁场穿过 该面元的磁通量为 dΦ=B·ds=oldz 矩形平面的总磁通量 Φ=dΦ 解由上述分析可得矩形平面的总磁通量 了器du=兴会 Φ d,2nx