
2一1一木块能在与水平面成&角的斜面上以匀速下滑.若使它以速率0 沿此斜面向上滑动,如图2-1()所示,试证明它能沿该斜面向上滑动的距离为 o/(4 gsin a). 分析动力学问题一般分为两类:(1) 已知物体受力求其运动情况:(2)已知物体 的运动情况来分析其所受的力,当然,在 个具体题目中,这两类问题并无截然的界 限,且都是以加速度作为中介,把动力学方 程和运动学规律联系起来.该题木块的下 (a) 1b) 滑过程属于后一类问题,而木块的上滑过 图2-1 程则属于前一类. 动力学问题的一般解题步骤可分为:(1)分析题意,确定研究对象,分析受 力,选定坐标;(2)根据物理的定理和定律列出原始方程组;(3)解方程组,得出文 字结果;(4)核对量纲,再代人数据,计算出结果来. 证选定木块为研究对象,其受力如图2一1(b)所示.取沿斜面向上为x轴 正向,由牛顿定律分别列出下滑、上滑过程的动力学方程 mgsin a-F=0 (1) -mgsin a-F=ma (2) 由式(2)知,加速度为一常量.由匀变速直线运动规律,有 v2=v6+2as (3) 解上述方程组,可得木块能上滑的距离 g=-爱=46

2-2假使地球自转速度加快到能使赤道上的物体处于失重状态,一昼夜 的时间有多长? 分析由于物体随地球自转时,有向心加速度存在.当提供此加速度的力即 为重力时,物体处于失重状态.由向心加速度和角速度的关系就可得一昼夜所需 的时间 解按题意有 mg =mra2 (1) T=2xw (2) 则地球自转一天所希时间为 T=2π√rg=5.07×103s≈1.4h
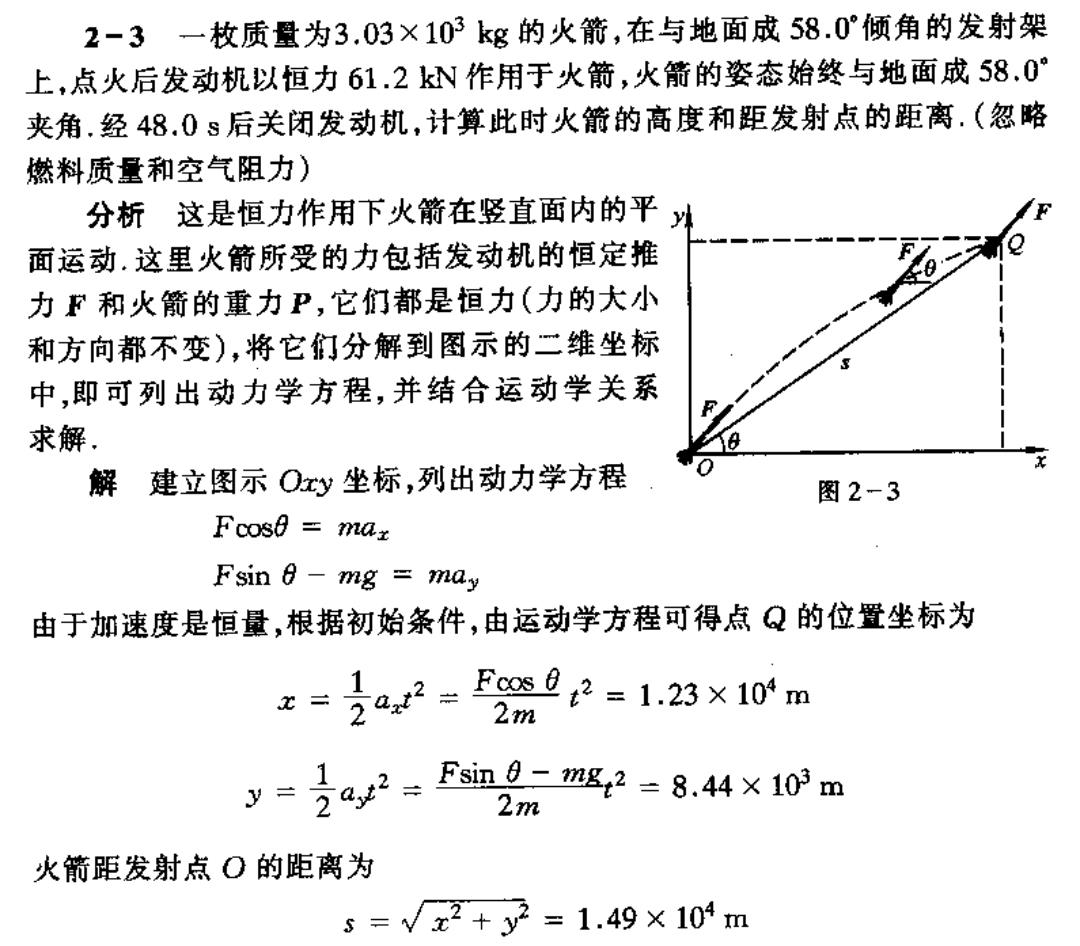
2-3一枚质量为3.03×103kg的火箭,在与地面成58.0°倾角的发射架 上,点火后发动机以恒力61.2kN作用于火箭,火箭的姿态始终与地面成58.0° 夹角,经48.0s后关闭发动机,计算此时火箭的高度和距发射点的距离.(忽略 燃料质量和空气阻力) 分析这是恒力作用下火箭在竖直面内的平 面运动.这里火箭所受的力包括发动机的恒定推 力F和火箭的重力P,它们都是桓力(力的大小 和方向都不变),将它们分解到图示的二维坐标 中,即可列出动力学方程,并结合运动学关系 求解. 解建立图示Oxy坐标,列出动力学方程 0 图2-3 Fcose maz Fsin 6-mg may 由于加速度是恒量,根据初始条件,由运动学方程可得点Q的位置坐标为 z=22=5222=1.23×10m 2m y=3a2=Fs029nm2=8.4×10m 1 2m 火箭距发射点O的距离为 s=√x2+y=1.49×104m
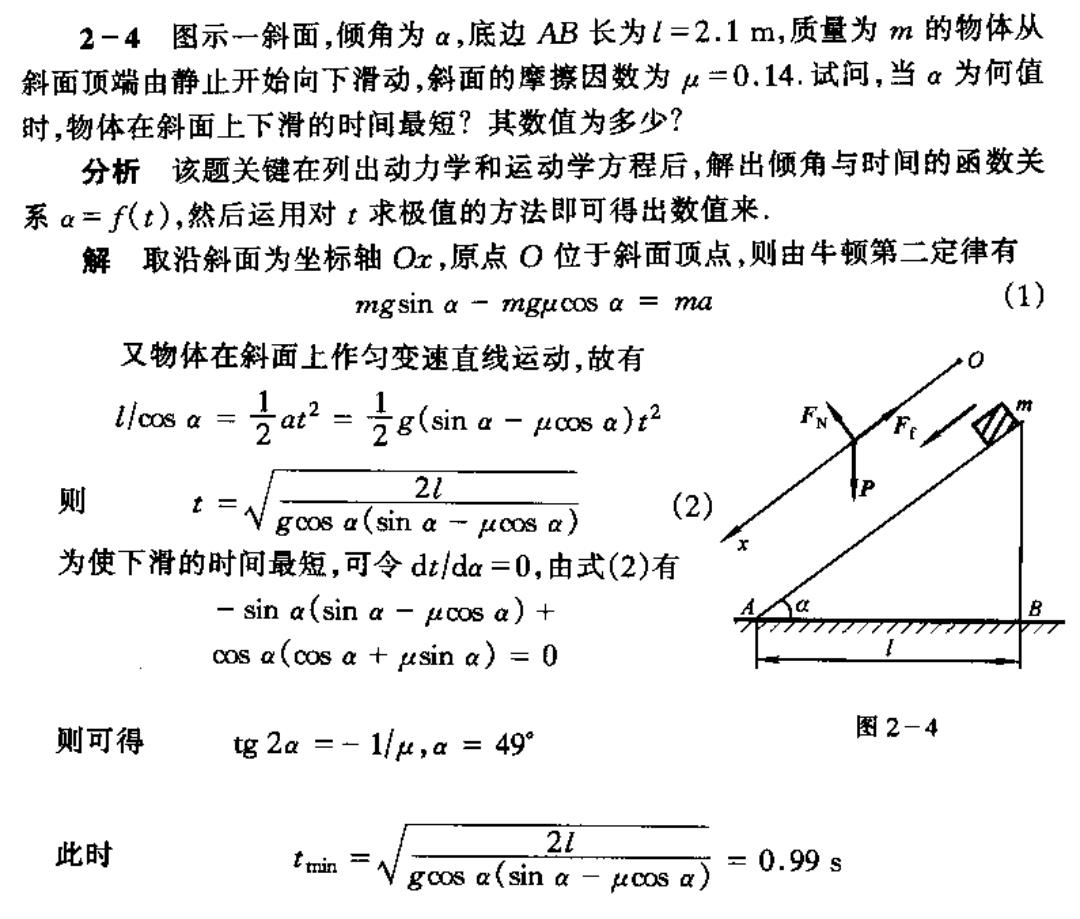
2-4图示一斜面,倾角为a,底边AB长为l=2.1m,质量为m的物体从 斜面顶端由静止开始向下滑动,斜面的摩擦因数为μ=0.14.试问,当a为何值 时,物体在斜面上下滑的时间最短?其数值为多少? 分析该题关键在列出动力学和运动学方程后,解出倾角与时间的函数关 系α=f(t),然后运用对t求极值的方法即可得出数值来. 解取沿斜面为坐标轴Ox,原点O位于斜面顶点,则由牛顿第二定律有 gsin a-7mgμcosa=na (1) 又物体在斜面上作匀变速直线运动,故有 lleos a =2a2=7g(sin a ucos a) 则 tgcos a(sin a-pcos a) (2) 为使下滑的时间最短,可令dt/da=0,由式(2)有 -sina(sina-ucos a)+ 7777777777777 cos a(cos a usin a)=0 则可得 tg2a=-1/u,a=49° 图2-4 此时 21 t恤=√gs(sin&-kosa=0.9s

2一5工地上有一吊车,将甲、乙两块混凝土预制板吊起送至高空.甲块质 量为m1=2,00×102kg,乙块质量为m2=1.00×102kg.设吊车、框架和钢丝绳 的质量不计.试求下述两种情况下,钢丝绳所受的张力以及乙块对甲块的作用 力:(1)两物块以10.0m's2的加速度上升;(2)两物块以1.0ms2的加速度上 升.从本题的结果,你能体会到起吊重物时必须缓慢加速的道理吗? 分析预制板、吊车框架、钢丝等可视为 一组物体.处理动力学问题通常采用“隔离体” 的方法,分析物体所受的各种作用力,在所选 定的惯性系中列出它们各自的动力学方程.根 据连接体中物体的多少可列出相应数目的方 程式.结合各物体之间的相互作用和联系,可 解决物体的运动或相互作用力. 图2-5 解按题意,可分别取吊车(含甲、乙)和 乙作为隔离体,画示力图,并取竖直向上为Oy轴正方向(图2-5).当框架以加 速度a上升时,有 Fr-(m1+m2)g=(m1+m2)a (1) Fn -m2g m2a (2) 解上述方程,得 Fr=(m1+m2)(g+a) (3) F2=m2(g+a) (4) (1)当整个装置以加速度a=10ms2上升时,由式(3)可得绳所受张力的 值为 Fr=5.94×103N 乙对甲的作用力为 Fe=-Fa=-m2(g+a)=-1.98×103N (2)当整个装置以加速度a=1ms2上升时,得绳张力的值为 Fr=3.24×103N 此时,乙对甲的作用力则为 Fa=-1.08×103N 由上述计算可见,在起吊相同重量的物体时,由于起吊加速度不同,绳中所 受张力也不同,加速度大,绳中张力也大.因此,起吊重物时必须缓慢加速,以确 保起吊过程的安全
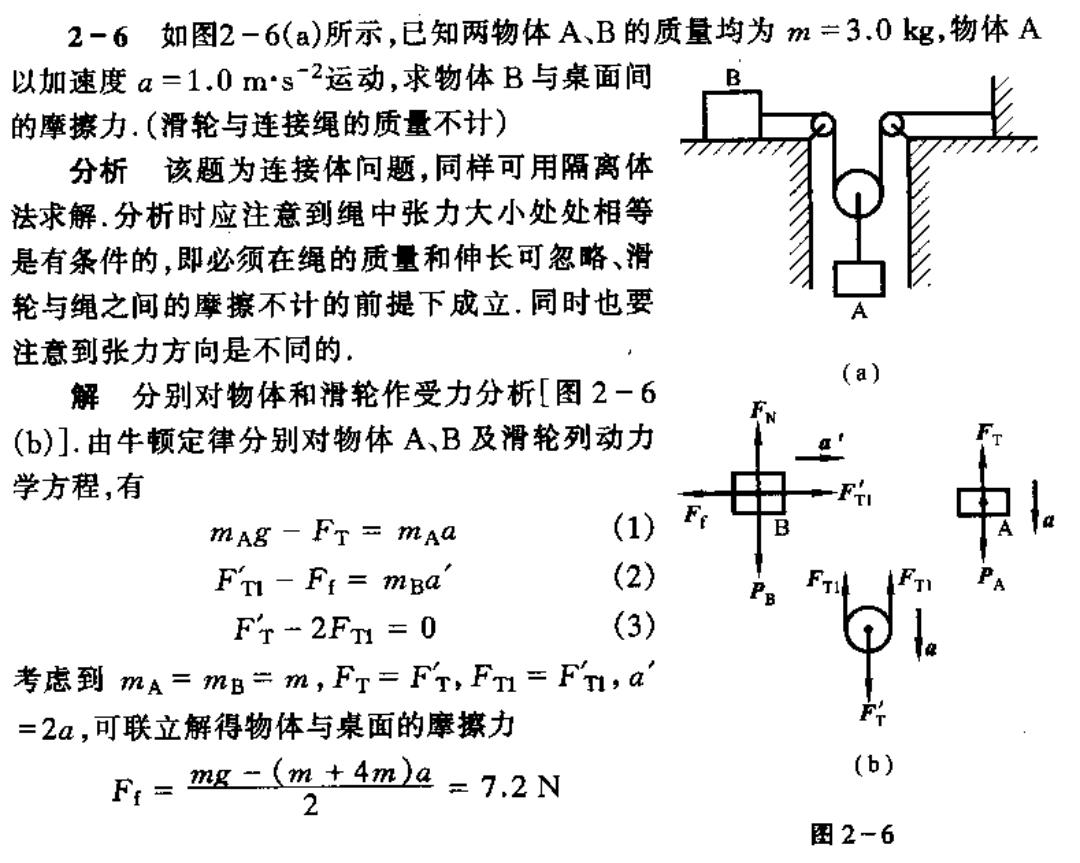
2-6如图2-6(a)所示,已知两物体A、B的质量均为m=3.0kg,物体A 以加速度a=1.0ms2运动,求物体B与桌面间 的摩擦力.(滑轮与连接绳的质量不计) 分析该题为连接体问题,同样可用隔离体 法求解.分析时应注意到绳中张力大小处处相等 是有条件的,即必须在绳的质量和伸长可忽略、滑 轮与绳之间的摩擦不计的前提下成立.同时也要 注意到张力方向是不同的。 解分别对物体和滑轮作受力分析[图2-6 (b)门.由牛顿定律分别对物体A、B及滑轮列动力 学方程,有 mAg -FT mAa (1) FTI-Fi=mBa' (2) F'T-2FTI =0 (3) 考虑到mA=mB=m,FT=F,FT=F,a =2a,可联立解得物体与桌面的摩擦力 F=mg-(m+4m=7,2N 2-6

2-7质量为m的长平板A以速度在光滑平面上作直线运动,现将质 量为m的木块B轻轻平稳地放在长平板上,板与木块之间的动摩擦因数为4, 求木块在长平板上滑行多远才能与板取得 B 共同速度? 分析当木块B平稳地轻轻放至运动 着的平板A上时,木块的初速度可视为零】 由于它与平板之间速度的差异而存在滑动 图2-7 摩擦力,该力将改变它们的运动状态.根据牛顿定律可得到它们各自相对地面的 加速度.换以平板为参考系来分析,此时,木块以初速度-。(与平板运动速率大 小相等、方向相反)作匀诚速运动,其加速度为相对加速度,按运动学公式即可 解得 该题也可应用第三章所讲述的系统的动能定理来解.将平板与木块作为系 统,该系统的动能由平板原有的动能变为木块和平板一起运动的动能,而它们的 共同速度可根据动量定理求得,又因为系统内只有摩擦力做功,根据系统的动能 定理,摩擦力的功应等于系统动能的增量.木块相对平板移动的距离即可求出. 解1以地面为参考系,在摩擦力F:=4g的作用下,根据牛顿定律分别 对木块、平板列出动力学方程 Fr=umg ma Fi=-Fr=m'a2 a1和a2分别是木块和木板相对地面参考系的加速度.若以木板为参考系,木块 相对平板的加速度a=a1+a2,木块相对平板以初速度-。作匀减速运动直至 最终停止.由运动学规律有 u'2=2a9 由上述各式可得木块相对于平板所移动的距离为 5=2g(m+m】 解2以木块和平板为系统,它们之间一对摩擦力的功为 W=Fi(s +1)-Fil umgs 式中1为平板相对地面移动的距离. 由于系统在水平方向上不受外力,当木块放至平板上时,根据动量守恒定 律,有 mv=(m+m) 由系统的动能定理,有 gmgs =mv2(m+m)v2 由上述各式可得 m'v2 s=2g(m+m】

2一8直升飞机的螺旋桨由两个对称的叶片组成.每一叶片的质量m= 136kg,长l=3.66m.求当它的转速n=320min时,两个叶片根部的张力. (设叶片是宽度一定、厚度均匀的薄片) Frr)drFi(r+dr) 图2-8 分析螺旋桨旋转时,叶片上各点的加速度不同,在其各部分两侧的张力也 不同;由于叶片的质量是连续分布的,在求叶片根部的张力时,可选取叶片上 小段,分析其受力,列出动力学方程,然后采用积分的方法求解。 解设叶片根部为原点O,沿叶片背离原点O的方向为正向,距原点O为 r处的长为dr一小段叶片,其两侧对它的拉力分别为Fr(r)与Fr(r+dr).叶 片转动时,该小段叶片作圆周运动,由牛顿定律有 dFT=Fr(r)-F(r+dr)=o2rdr 由于r=1时外侧FT=0,所以有 F()=-27(2-)=-2(2-2) 上式中取r=0,即得叶片根部的张力 Fm=-2.79×105N 负号表示张力方向与坐标方向相反
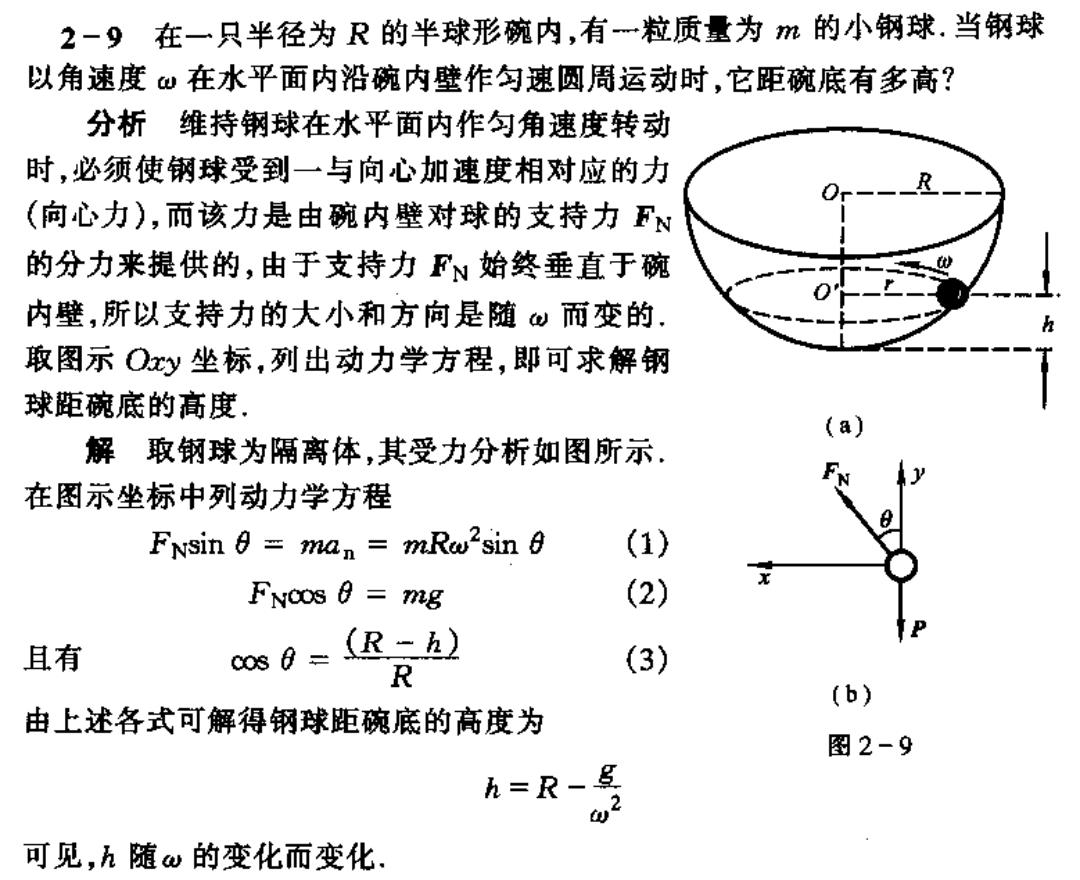
2-9在一只半径为R的半球形碗内,有一粒质量为m的小钢球.当钢球 以角速度。在水平面内沿碗内壁作匀速圆周运动时,它距碗底有多高? 分析维持钢球在水平面内作匀角速度转动 时,必须使钢球受到一与向心加速度相对应的力 (向心力),而该力是由碗内壁对球的支持力FN 的分力来提供的,由于支持力FN始终垂直于碗 内壁,所以支持力的大小和方向是随w而变的」 取图示Oy坐标,列出动力学方程,即可求解钢 球距碗底的高度 解取钢球为隔离体,其受力分析如图所示, 在图示坐标中列动力学方程 FNsin =man mRw2sin 8 (1) FNC0S 0 =mg (2) 且有 c080=(R-h) R ⊙ (b) 由上述各式可解得钢球距碗底的高度为 图2-9 h=R- 可见,h随w的变化而变化

2-10 一质量为m的小球最初位于如图2-10(a)所示的A点,然后沿半 径为r的光滑圆轨道ADCB下滑.试求小球到达点C时的角速度和对圆轨道的 作用力. 分析该题可由牛顿第二定律求解,在取自然坐标的情况下,沿圆弧方向的 加速度就是切向加速度a,与其相对应的外力F,是重力的切向分量mgsin a, 而与法向加速度an相对应的外力是支持力FN和重力的法向分量mg cos a.由 此,可分别列出切向和法向的动力学方程F,=mduldt和F.=aa由于小球 在滑动过程中加速度不是恒定的,因此,箫应用积分求解,为使运算简便,可转换 积分变量, “该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的 速度和角速度,方法比较简便.但它不能直接给出小球与圆弧表面之间的作用 力 解小球在运动过程中受到重力P和圆轨道对它的支持力F.取图2“10 (6)所示的自然坐标系,由牛领定律得 F--mgsin a -m (1) F-FN-mgcos a- (2)7 由v出=出,得=出,代人式1,并根据 小球从点A运动到点C的始末条件,进行积分, 0 有 (a) 0odo=n←gnea加 t=√2 rgcos a 则小球在点C的角速度为 ==(2gcos a)Tr 由式(2)得 F mgcm a=3mgoe a (b) 由此可得小球对圆轨道的作用力为 图2-10 FN'=-FN =-3mgcos a 负号表示FN与ea反向