
16-1一个10H的线圈与两个电容为5.0pF和20.0pF的电容器分别 构成LC电路,问固有振荡频率各为多少? 分析在LC电路中,一且有能量激发(如开始时电容器上带电荷),则在回 路中将有周期性变化的电流.此时极板上电荷的变化满足方程dq/dt2+wq= 0,这与力学中简谐运动的傲分方程相似,其中w=1/√LC称为LC振荡电路的 固有振荡角频率,利用该式即可求解. 解由分析可得LC电路的振荡频率为 v=尝=2x元 当线圈自感L=10H,电容分别为C1=5.0pF和C2=20.0pF时,LC电路的 固有振荡频率分别为 1=1/2π√C1=2.25×10?z 2=1/2π√LC2=1.13×103Hz

16-2在一个LC振荡电路中,若电容两极板上的交变电压U=(50V) cos(10πs1)t,电容C=1.0×10-7F,电路中的电阻可以忽略不计.求:(1)振 荡的周期;(2)电路中的自感;(3)电路中的电流随时间变化的规律. 分析在不计电阻的前提下,该LC电路是无阻尼自由振荡电路,在振荡过 程中电容器两极板上的电压、电荷及电路中的电流均以相同的周期变化着.振荡 周期为T=2π√LC.因此,本题可通过已知的电压的角频率w,求出振荡周期, 然后可求出自感L·另外,电容器极板上电压U、电荷g始终满足关系式q= CU.因此,在确定q=q(t)后,根据电流定义I=dqdt,可求出电流的变化规 律. 解(1)从题中已知的电压变化关系中得振荡周期为 T=2x/w=2.0×10-4s (2)由振荡电路周期T=2π√LC得电路中的自感为 L=T2142C=1.01×10-2H (3)电路中电流随时间变化的规律为 I=dg/dt=C·dUU/dt=-(0.157A)sin(104πs1)t

16-3若收音机调谐电路所用的线圈自感为260H,要想收听到535kz 到1605kHz的广播,问与线圈相连接的电容的最大值和最小值各应为多少? 分析该调谐电路实为LC振荡电路,其频率为y=1/2π√LC.当自感L 一定时,调谐频率越高,所需电容越小。 解由分析可知,当L一定时,对应于最低收听频率ym=535kHz所需电 容的值为 Cmnx 422nL=340pF 对应于最高收听频率ymx=1605kHz,所需电容的值为 Coin4 vi L =37,8F

16-4用一个电容可在10.0pF到360.0pF范围内变化的电容器和一个 自感线圈并联组成无线电收音机的调谐电路.(1)该调谐电路可以接收的最大和 最小频率之比是多少?(2)为了使调谐频率能在5.0×10Hz到1.5×10Hz的 频率范围内,需在原电容器上并联一个多大的电容?此电路选用的自感应为多 大? 分析参见上题的分析,当自感L一定时,要改变调谐频率的范围,只斋改 变电容的变化范围.本题采用并联电容C的方法使电容由原有的变化范围C ~C改变为Cmm+C~Cma+C,从而达到新的调谐目的.为此,可根据v= 1/2π√LC,由原有电容比Cmax/Cnin来确定对应的频率比ymax/ymin.再由新要求 的频率比来确定需要并联的电容的大小. 解(1)当线圈自感L一定时,由v=1/2π√LC,可得 yma/ymin÷√CC=6.0 (2)为了在5.0×10Hz一1.5×10°Hz的频率范围内调谐,应满足 v'ma/yi=√(Cmx+C)(Cmi血+C) 由此得在原电容器上需并联的电容为 C=Cmg-Cn(yey (ma/Vinin)2-1 -=33.75pF 此电路选用的线圈自感为 L =1/4122C =1/4n2vin Cmox +C) =2.58×10-4H
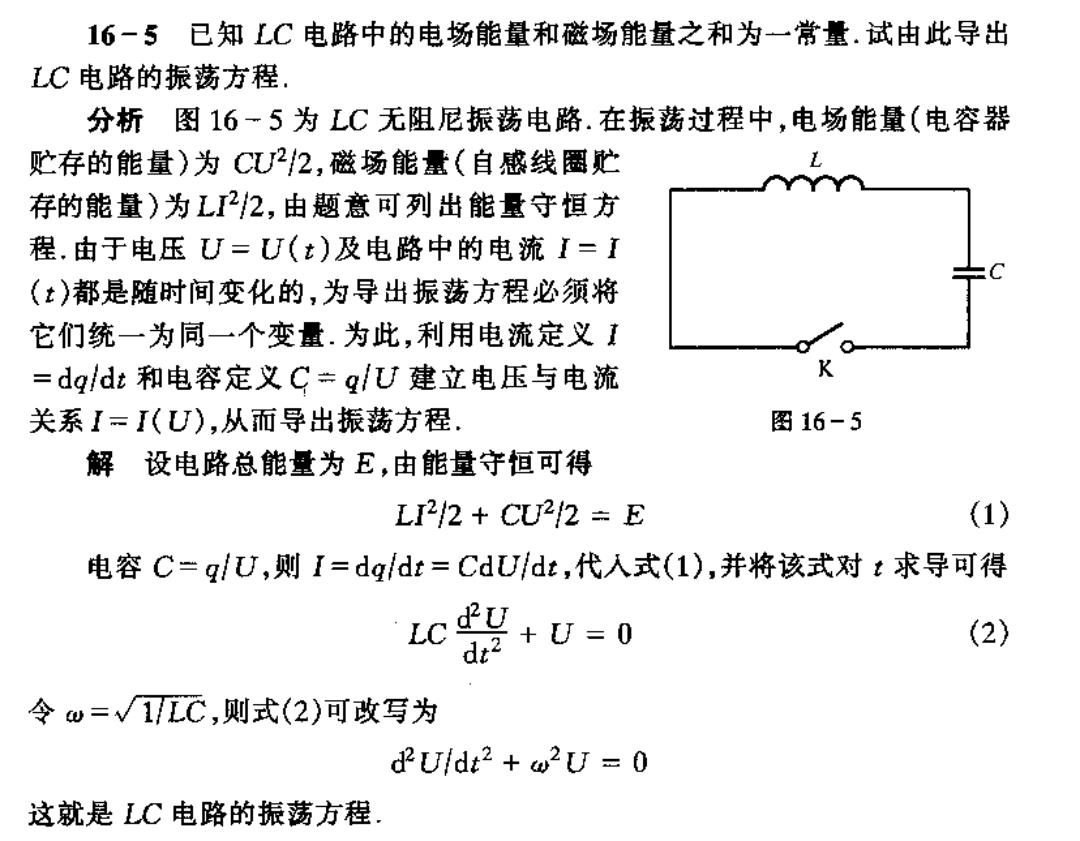
16-5已知LC电路中的电场能量和磁场能量之和为一常量.试由此导出 LC电路的振荡方程 分析图16-5为LC无阻尼振荡电路.在振荡过程中,电场能量(电容器 贮存的能量)为C22,磁场能量(自感线圈贮 存的能量)为L2,由题意可列出能量守恒方 程.由于电压U=U(t)及电路中的电流I=I (t)都是随时间变化的,为导出振荡方程必须将 它们统一为同一个变量.为此,利用电流定义1 =dq/dt和电容定义C=g/U建立电压与电流 关系I=I(U),从而导出振荡方程. 图16-5 解设电路总能量为E,由能量守恒可得 L22+CLU22÷E (1) 电容C=q/U,则I=dq/dt=CdU/dt,代入式(1),并将该式对t求导可得 c器+U=0 (2) 令w=√1C,则式(2)可改写为 d2Uldt2+w2U=0 这就是LC电路的振荡方程

16-6在上题图16-5中,如果C=100.0pF,L=400H.设K刚关闭 时,电容器两极板的电势差为1.0V,且电路中的电流为零,求:(1)振荡频率; (2)最大电流:(3)线圈中的最大磁场能量, 分析(1)振荡频率由电路中L、C的值决定,即y=12元√LC.(2)根据 题意,起始时电容器极板上的电势差Uo=1.0V,且电路中电流为零,因而此时 极板上有最大电荷值q0=CU0.在振荡过程中电荷随时间作周期性变化,且有q =gocos(at+),利用电流定义I=dq/dt,即可求得电路中的最大电流值.(3) 在LC无阻尼自由振荡电路中,电场能量和磁场能量交替变化,线圈中的最大磁 场能量L品x2(也等于储存在电容器中的最大电场能量CLU及x2)就是电路中 的总能量. 解(1)该LC电路的振荡频率为 y=1/2π√LC=7.96×105Hz (2)电路中的最大电流为 Imax =(dqldt)max =wgo=aCUo =5.0×104A (3)线圈中的最大磁场能量为 E=LI径2=CU2 =5.0×1011J

16-7在LC振荡电路中,电容C=10.0pF,自感L=20.0H,电容器两 极板的最大电势差Ux=1.0V.求电场能量和磁场能量相等时电路中的电流 值和电容器上的电荷。 分析振荡电路中电场和磁场能量是相互转化的,但总能量不变,且等于最 大的电场能C只✉2或最大的磁场能Lx2.而任一时刻电场和磁场能分别为 Ee=CU22=q22C和Em=L2.当磁场能量和电场能量相等时,它们均等于 总能量的一半.根据题给条件即可求解。 解根据题意,有 g22C=号(CUax2) L22=2(CUx2) 多 g=CUmW2=7.07×10-12C 1=√/C2LUms=5.0×10-+A

16-8一振荡电路,已知C=0.025F,L=1.015H.电路中电阻可忽略 不计,电容器上电荷最大值为Q0=2,5×106C.(1)写出电路接通后电容器两 极板间的电势差随时间而变化的方程和电路中电流随时间而变化的方程;(2)写 出电场的能量、磁场能量及总能量随时间而变化的方程;(3)求t1=T8和t2= T4时,电容器两极板间的电势差、电路中的电流、电场能、磁场能。 分析无阻尼LC振荡电路中电流、电容器极板上电荷以及电势差均以相 同的频率随时间作正弦或余弦变化.如果令极板上电荷q=Qoas(t+0),则 由1=dqdt、U=g/C可得电路中的电流I、极板两端电势差U的变化规律.利 用电磁场中电场能量和磁场能量公式可写出它们随时间:的函数关系式和特定 时刻的瞬时值 解(1)LC无阻尼振荡电路的振荡角频率为 w=1/√LC=2000xs1 若以电路闭合的瞬间为计时起点,此时极板上电荷最大.则任一时刻极板上的电 荷为 9=Q0 cos wt=(2.5×10-6C)cos(2000rsl): 该时刻电路中的电流为 I=dq/dt=-(1.57×10-2A)sin(2000πs1)t 极板两端电势差为 U=g/C=(100V)os(2000πs1)t (2)任意时刻电场能量、磁场能量及总能量分别为 E。=q2f2C=(1.25×104J)cos2(2000πs1)t Em=L2f2=(1.25×10-4J)sin2(2000xs1)t E=E。+Em=1.25×10-4J (3)由w=2xv=2πT,可得T=0.001s.则当t1=T8时,由上述各式可 U1=(100V)cos[(2000πs1)T8]=70.7V I1=-(1.57×10-2A)sin[(2000ms1)T/8]=-1.11×10-2A E1=(1.25×10-4J)cos2[(2000πs1)T8]=6.25×10-5J Eml=(1.25×104J)si2[(2000xs1)T8]=6.25×10-3j 同理,当t2=T4时可得 U2=0;l2=-1.57×102A:Ea=0;E2=1.25×104J 由上述结果可以看出LC电路在无阻尼振荡过程中,总的电磁场能量是不 变的,即满足能量守恒定律

16-9一广播电台的辐射功率是10kW,假定辐射场均匀分布在以电台为 中心的半球面上.(1)求距离电台为r=10km处的坡印廷矢量的平均值;(2)若 在上述距离处的电磁波可看作平面波,求该处的电场强度和磁场强度的振幅. 分析坡印廷矢量是电磁波的能流密度矢量,它是随时间作周期性变化的, 求其平均值,也就是指在一周期内的平均值.在忽略电磁波传播过程中的能量损 耗时,按题意,波源的辐射功率就应等于单位时间通过半球面(面积A=2π2) 的电滋波能量,即P=S·A,而平均能流密度值=E五.另外,由电磁波的性质 可知,E与H垂直,相位相同,且有关系式√EaE=√oH.因此,平面电磁波的 玻印廷矢量大小的平均值可表示为S=方E。=2√会品.由此可求电场强 度振幅E和磁场强度振幅Hm: 解(1)因为辐射场分布在半球面上,则坡印廷矢量的平均值为 S=P/2rx2=1.59×10-sW.m-2 2》根器分折,5=E百=E队,2=2兽品,则磁扬强度和电场强度的 振幅分别为 Hm=(2S√o)12=2.91×104A·m1 Em=25Hm=0.109V·m-1

16-10目前普及型晶体管收音机的中波灵敏度(指平均电场强度E)约 为1.0×10-3V·m1.设收音机能清楚地收听到1.0×103m远处某电台的广 播,该台的发射是各向同性的(以球面形式发射),并且电磁波在传播时没有损 耗,问该台发射的功率至少有多大? 分析由上题分析可知,电台发射功率P=·A(由于电磁波以球面形式 发射,因此本题中A=4πr).而根据收音机的灵敏度(即平均电场强度E)及关 系式√eE=√oH,由S=E方可求得5, 解由上述分析知道,坡印廷矢量的平均值为 S=EF=√eo/E2=2.65×109W·m2 则电台最小的发射功率为 P=4rr2.5=3.3×104W