
13-1如图所示,在磁感强度B=7.6×104T的均匀磁场中,放登个 线圈.此线圈由两个半径均为3.7cm且相互 垂直的半圆构成,磁感强度的方向与两半圆 平面的夹角分别为62°和28°,若在4.5×10~3 s的时间内磁场突然减至零,试问在此线圈内 的感应电动势为多少? 分析由各种原因在回路中所引起的感 应电动势,均可由法拉第电磁感应定律求解, 即(=一曾=品引B·5,但在求解时应注 意下列几个问题: 图13-1 1.回路必须是闭合的,所求得的电动势为回路的总电动势 2.中应该是回路在任意时刻或任意位置处的磁通量.它由少=B·S 计算.对于均匀磁场则有中=}B·dS=-BScos6,其中Sccs8=S1为闭合回 路在垂直于磁场的平面内的投影面积.对于本题,重=BS1cos01+BS2o862,式 中1和2为两半圆形平面法线en与B之间的夹角. 3.感应电动势的方向可由一P来判定,散材中已给出判定方法为方便起 见,所取回路的正向(顺时针或逆时针)应与穿过回路的B的方向满足右螺旋关 系,此时更恒为正值,这对符号确定较为有利 解迎着B的方向,取逆时针为线圈回路的正向.由法拉第电磁感应定律 g=一2-是(asos+BS,w)-8(S+sos62) 三-82(S,os9+52s1=4.91X10-4V >0,说明感应电动势方向与回路正向一致

13一2一铁心上绕有线圈100匝,已知铁心中磁通量与时间的关系为更= (8.0×105Wb)sin(100衣91)t,求在t=1.0×10-2s时,线圈中的感应电动 势. 分析由于线圈有N匝相同回路,线圈中的感应电动势等于各匝回路的感 应电动势的代数和,在此情况下,法拉第电磁感应定律通常写成=-N9、 dt 一铝,其中单=0叫篮链, 解线圈中总的感应电动势 8=N8盟=(2.51Vas(100元s6 当t=1.0×102s时,后=2.51V

13一3如图所示,用一根硬导线弯成半径为r的一个半圆.使这根半圆形 导线在磁感强度为B的匀强磁场中以频率∫ 旋转,整个电路的电阻为R,求感应电流的表 达式和最大值. 分析由题意知,穿过图示闭合回路中面 积为S=方2的半圆形导线部分的磁通量 在不断变化,在任意时刻这部分磁通量中(t) =BScos日,所以必须找出8=6(t)的关系式. 为此,设图示位置为守线在初始时刻(即t三 图13-3 0)的位置,顺时针方向为回路正向,此时半圆形导线平面的法线与B之间的夹 时间后,6=2x.将上述关系代人=一华,求得同 刻的电动势(t),再用欧姆定律求得相应的感应电流I(t),进而求得最大值 Im·另外,由于本题磁场不随时间变化,只是半圆形导线在旋转,因此产生的电 动势是动生电动势,所以也可在线圈处于任意位置时用公式=}(”×B)·d 来求解, 解根据分析,由丁磁场是均匀的,故任意时刻穿过回路的磁通量为 (t)=BSc00=Bcos 2mf 根据法拉第电磁像应定辣,有《=一肥B血2x 因此E路中的感成电藏为1:)=景-安n2分 则感应电流的最大值为 In= 22B R

13-4有两根相距为d的无限长平行直导线,它们通以大小相等流向相 反的电流,且电流均以的变化率罐长.若有 一边长为d的正方形线圈与两导线处于同 一平面内,如图所示.求线圈中的感应电动 热 分析本题仍可用法拉第电磁感应定律 。=一普来求解由于回路处在非均匀磁场 中,磁通量就需用中=」B·S来计算(其 中B为两无限长直电流单独存在时产生的磁 图13-4 感强度B1与B2之和). 为了积分的需要,建立如图13-4所示的坐标系.由于B仅与x有关,即B =B(x),故取一个平行于长直导线的宽为dx、长为d的面元dS,如图中阴影 部分所示,则dS=ddx,所以,总磁通最可通过线积分求得(若取面元dS= dxdy,则上述积分实际上为二重积分).本题在工程技术中又称为互感现象,也 可用公式=一M求解 解1穿过面元dS的磁通量为 d0=Bds=B1ds+Bd5=2a200d- 因此穿过线圈的磁通量为 。=jo-2z0t-2-兴n是 gold 再由法拉第电磁感应定律,有 6=--(%器n号)鼎 解2当两长直导线有电流【通过时,穿过线圈的磁通量为 =2盟如子 线圈与两长直导线间的互感为 M=票=%2n 当电流以出交化时,线圈中的互感电动势为 8=-M-(n)鼎 讨论本题中如线圈又以速率。沿水平向右运动,如何用法拉第电磁感应 定律求图示位置的电动势呢? 此时线圈中既有动生电动势,又有感生电动势设时刻t,线圈左端距右侧 直导线的距离为,则穿过回路的磁通量重二B·dS=f八I,),它表现为变 量【和的二元函数,将西代人6一吧即可求解,求解时应按复合函数求导, 注意,其中=口,再令=d即可求得图示位置处回路中的总电动势.最终结 果为两项,其中-一项为动生电动势,另一项为感生电动势

13-5有一测量磁感强度的线图,其截面积S=4.0c12、匝数N=160 匝、电阻R=502.线与一内阻R:=302的冲击电流计相连.若开始时,线圈 的平面与均匀磁扬的磁感强度B相垂直,然后线圈的平面很快地转到与B的方 向平行,此时从冲击电流计中测得电荷值q=4.0×105C.问此均匀磁场的磁 感强度B的值为多少? 分析在电磁感应现象中,闭合回路中的感应电动势和感应电流与磁通量 变化的快慢有关,而在一段时间内,通过导体戴面的感应电量只与磁通量变化的 大小有关,与磁通量变化的快慢无关.工程中常通过感应电量的测定来确定磁场 的强弱 解在线圈转过90°角时,通过线圈平面磁通量的变化量为 △中=p2-1=NBS-0-NBS 因此,流过导体截面的电量为9=K+RR+R △Φ NBS B=尽tR2=0.050T NS

13-6如图所示,一长直导线中通有=5.0A的电流,在距导线9.0c 处,放一面积为0.102,10匝的小圆线圈,线圈中的磁场可看作是均匀的.今 在1.0×10-2s内把此线圈移至距长直导线10.0cm处.求:(1)线圈中平均感 应电动势;(2)设线圈的电阻为1.0×10~2,求通过线图横截面的感应电荷。 分析虽然线嚼处于非均匀磁扬中,但由于线圈的面积很小,可近似认为穿 过线图平面的磁场是均匀的,因而可近似用亚二BS来计算线圈在始、末两个 位蛋的磁链, 解(1)在始、末状态,通过线圈的磁链分别为 =MS=2S,=8s=5 则线瑙中的平均感应电动势为 剧=器=只》-1×wv 电动势的指向为顺时针方向, 9.0 cm (2)通过线图导线機截面的感应电荷为 g=g,-=a4=1.1×08C 图13-6

13-7如图13-7(a)所示,把一半径为R的 半圆形导线里置于磁感强度为B的均匀磁场中, 当导线以速率v水平向右平动时,求导线中惑应 电动势8的大小,哪一端电势较高? 分析本题及后面几题中的电动势均为动生 电动势,除仍可决R=一 求解外(必须设法构造 dt 一个闭合回路,还可直接用公式6=】,(知×)·1求解.在用后一种方达求解 时,应注意下列几个问题: 1.式中(v×B》dl为导体上任一导线元dl.上的动生电动势d滤,积分表 示对导线上所有的导线元产生的电动势求和 2.需建立一个适当的坐标系(尽可能利用其对称性),在导体上任意位置处 取导线元dl,写出dl处的。与B的表达式,并明确两个角度,即d!处的和与 B的夹角,以及矢量(。×B)与d!间的夹角,在一般情况下,上述各量可能是dl 所在位置的函数 3.矢量(×B)的方向就是导线中电势升高的方向. 解1如图13-7(化)所示,假想半圆形导线OP在宽为2R的静止汇形导轨 上滑动,两者之问形成-·个闭合回路.设顺时针方向为回路正向,任一时刻端点 O或端点P距C形导轨左侧距离为x,则 币=(2Re+2R2B 即 6=-9=-2RB¥-2ReB 由于静止的C形导软上的电动势为零,则8=-2RB.式中负号表示电动势的 方向为逆时针,对OP段来说端点P的电势较高 解2建立如图13一7(©)所示的坐标系,在导体上任意处取导体元d山,则 d6=(×B)·dl=Bsin90°cos9dl=Buos6Rd0 (b】 图13-7 2 -jde-BRo 0de -2RuB 由矢量(×B)的指向可知,端点P的电势较高 解3连接OP使导线构成一个闭合回路.由于磁畅是均匀的,在任意时 刻,穿过回路的磁通量中=BS=常数.由法拉第电磁感应定律一 地可知, d: 6=0 又因 6s0+6o 即 p=-o 2RuB 由上述结果可知,在均匀磁场中,任意闭合导体回路平动所产生的动生电动 势为零;而任意曲线形导体上的动生电动势就等于其两端所连直线形导体上的 动生电动势.上述求解方法是叠加思想的逆运用,即补偿的方法
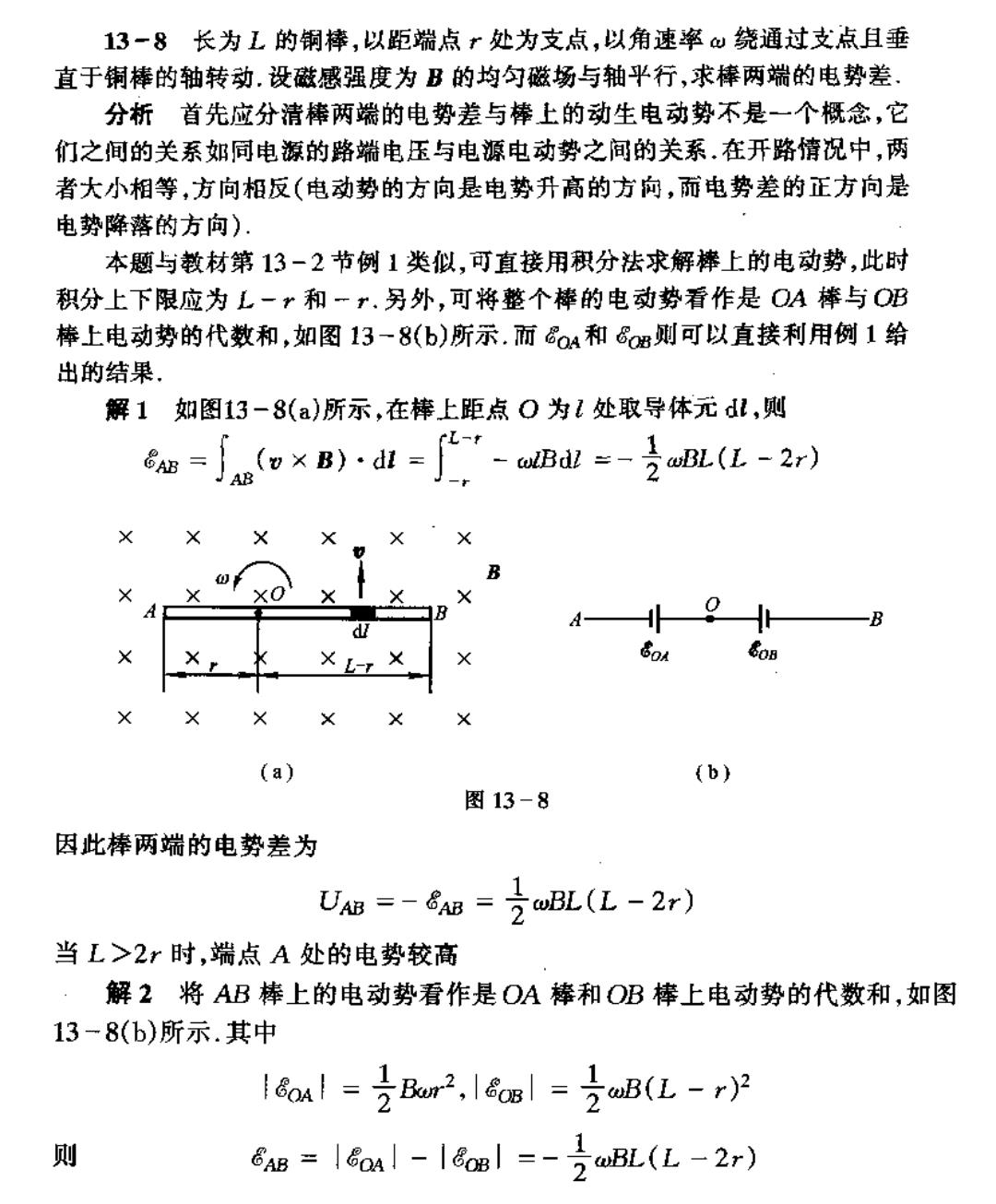
13一8长为L的铜棒,以距瑞点r处为支点,以角速率如绕通过支点且垂 直于铜棒的轴转动.设磁感强度为B的均匀磁场与轴平行,求棒两端的电势差. 分析首先应分清棒两端的电势差与棒上的动生电动势不是一个概念,它 们之间的关系如同电源的路端电压与电源电动势之间的关系.在开路情况中,两 者大小相等,方向相反(电动势的方向是电势升高的方向,而电势差的正方向是 电势降落的方向) 本题与教材第13-2节例1类似,可直接用积分祛求解棒上的电动势,此时 积分上下限应为L-r和一r,另外,可将整个棒的电动势看作是QA棒与OB 棒上电动势的代数和,如图13一8(b)所示.而a4和6s则可以直接利用例1给 出的结果, 解1如图13-8(a)所示,在棒上距点O为l处取导体元dl,则 6w=jo×B)·dl=j,-onas-L(L-2r) (b) 图13-8 因此棒两端的电势差为 UAn =-5a =oBL(L-2r) 当L>2r时,端点A处的电势较高 解2将AB棒上的电动势看作是OA棒和OB棒上电动势的代数和,如图 13-8(b)所示.其中 16o!=Bor2,I col =ToB(L-r) 则 6nB Icanl -lconl =-TBL(L-2r)

13-9如图所示,长为L的导体棒OP,处于均匀磁场中,并绕O0轴以角 速度ω旋转,棒与转轴间夹角恒为8,磁感强度B 与转轴平行.求OP棒在图示位置处的电动势。 分析如前所述,本题既可以用法拉第电磁感 应定律后一一地计算(但此时必须构造一个包含 dt OP导体在内的闭合回路,如直角三角形导体回路 OPQO),也可用8=,(o×B)·dl来计算.由于对 称性,导体OP旋转至任何位置时产生的电动势与 图示位置是相同的。 解1由上分析,得 ae=Joe(x):dl 图13-9 uBsin 90'cos adl =(Isin &Bcos(90-0)dl 由欠量(。×B)的方向可知嘴点P的电势较高, 解2设想导体OP为直角三角形导体回路OPQO中的一部分,任一时刻 穿过回路的磁通量中为零,则回路的总电动势 =0=e+0+ao 6ad 显然,8ao=0,所以 for =-6rg lop =o(PQ)2uB(Lsin 0)2 由上可知,导体棒OP旋转时,在单位时间内切割的磁感线数与导体棒QP等 效.后者是垂直切制的情况

13-10如图13-10(a)所示,金属杆AB以匀速0=2.0m81平行干 长直导线移动,此导线通有电流【=40A问:此杆中的感应电动势为多大?杆 的娜一端电势较高? (b) 图13-10 分析本题可用两种方法求解.(1)用公式6=(0×B)·dl求解,可建立 图13-10(a)所示的坐标系,所取号体元dl=dc,该处的磁感强度B=公 (2)用法拉第电磁感应定律求解,需构造一个包含杆AB在内的闭合回路.为此 可设想杆AB在一个静止的L山形导轨上滑动,如图13一10(b)所示.设时刻t,杆 AB距导轨下端CD的距离为y,先用公式巾=}B·dS求得穿过该回路的磁通 量,再代人公式台三一普即可求得回路的电动势,本即本题杆中的电动势。 解1根据分析,杆中的感应电动势为 式中负号表示电动势方向由B指向A,故点A电势较高 解2设顺时针方向为回路ABCD的正向,根据分析,在距直导线x处,取 宽为dx、长为y的面元dS,则穿过面元的磁通量为 d地=B·ds=2dx 401 穿过回路的磁通量为 回路的电动势为 8=--h1=-21=-3.4×105v 由于静止的山形导轨上电动势为零,所以 8a短=8=-3.84×10-5V 式中负号说明回路电动势方向为逆时针,对AB导体来说,电动势方向应由B 指向A,故点A电势较高