
C。两种情况都作诺动 ,并求振动期
学院: 班级: 姓名: 学号: — 61 — 14-1 一弹簧振子,当把它水平放置时,它作谐振动。若把它竖直放置或放在光滑斜面上, 试判断下面哪种情况是正确的?[ ] A.竖直放置作谐振动,放在光滑斜面上不作谐振动; B.竖直放置不作谐振动,放在光滑斜面上作谐振动; C.两种情况都作谐振动; D.两种情况都不作谐振动。 14-2 一远洋货轮,质量为 m,浮在水面时其水平截面积为 S,设在水面附近货轮的水平截面 积近似相等,设水的密度为 ,且不计水的粘滞阻力,证明货轮在水中作振幅较小的竖直自 由运动是简谐运动,并求振动周期

43如图示,顾量为100X10怎的f弹,以500m·的速度射入并酸在木块中,同时 恐 为x轴正向,求荷运动方程。 m77777777777 777777777777 -62
学院: 班级: 姓名: 学号: — 62 — 14-3 如图所示,质量为 1.00×10—2kg 的子弹,以 500m·s —1 的速度射入并嵌在木块中,同时 使弹簧压缩从而作简谐运动。设木 块的质量为 4.99kg,弹簧的劲度系 数为 8.00×103N·m —1。若以弹簧原 长时物体所在处为坐标原点,向左 为 x 轴正向,求简谐运动方程
学猴 一学号 14-4一水平弹簧扳子,振幅为4.0×10m,频率为0.5Hz,当1=0时,物体的状态是:(1)过 平衡位置向正方向运动:()在正方向的端点:()过A2处向负方向运动。试用读转矢量法确定 以上三种情况的初相,并写出谐振动方程, 15一两点作谐板动,周期为T。当它由平衡位置向x轴正方向运动时,从二分之一最大位 移处到最大位移处这段路保所需要的时间为]: ,m3) A.T/4 B.T/12 C.T6 D.T8 m 146一质点作简谐振动,其运动速度与时问的曲线 如右图所示。若质点的椒动规律用余弦函数描述, 则其初位相应为】 t/s A.工6B.Sn6 C.-5x6 D.-x6 E.-2T3 147已知某简谐振动的振动曲线如图所示。则此谐振动的振动方程为列 知.2 A.x 2cos( ,+,x)cm 33 B.x=2c08 2nt 2 元)cm 33 C.x=2cos 4π1,2 +二r)cm 33 D.x=2co9(33 4x2 --.T》Cm E.x=2cos(- t)cm 341 —63
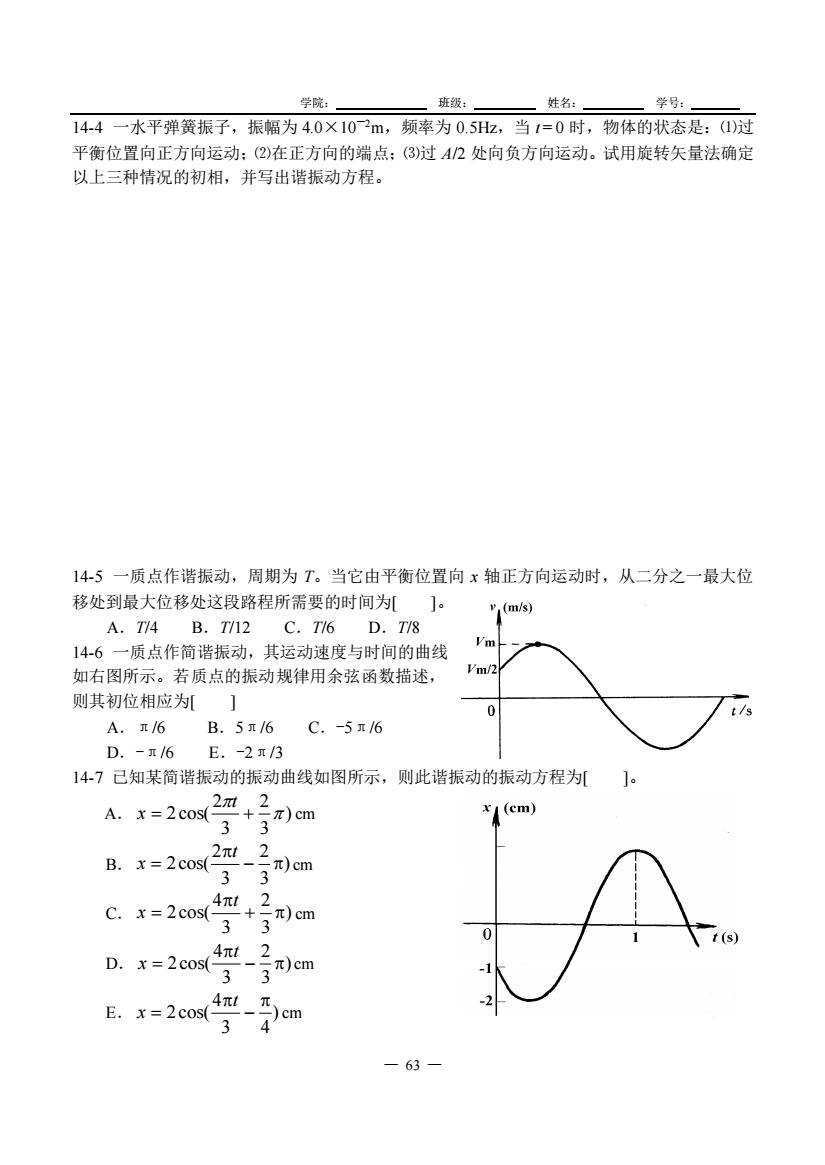
学院: 班级: 姓名: 学号: — 63 — 14-4 一水平弹簧振子,振幅为 4.0×10—2m,频率为 0.5Hz,当 t = 0 时,物体的状态是:⑴过 平衡位置向正方向运动;⑵在正方向的端点;⑶过 A/2 处向负方向运动。试用旋转矢量法确定 以上三种情况的初相,并写出谐振动方程。 14-5 一质点作谐振动,周期为 T。当它由平衡位置向 x 轴正方向运动时,从二分之一最大位 移处到最大位移处这段路程所需要的时间为[ ]。 A.T/4 B.T/12 C.T/6 D.T/8 14-6 一质点作简谐振动,其运动速度与时间的曲线 如右图所示。若质点的振动规律用余弦函数描述, 则其初位相应为[ ] A.π/6 B.5π/6 C.-5π/6 D.-π/6 E.-2π/3 14-7 已知某简谐振动的振动曲线如图所示,则此谐振动的振动方程为[ ]。 A. ) 3 2 3 2 2cos( = + t x cm B. ) 3 2 3 2 2cos( − = t x cm C. ) 3 2 3 4 2cos( + = t x cm D. ) 3 2 3 4 2cos( − = t x cm E. ) 3 4 4 2cos( − = t x cm
学辰: :外名:一 14-8一物体沿x轴作简诺运动,板幅为0.06m,周期为2.03,当1=0时位移为003m,且向x 轴正向运动。求:1)1-0.5s时,物体的位移、速度和加速度:(②物体从x一-0.03m处向x 轴负向运动开始,到平衡位置,至少减要多少时问? 149在一0时,周期为T,振幅为A的单摆分划处于 图(a)、(b小、()三种状态,若选单要的平衡位置为x朝 的原点,x轴指向正右方,则单摆作小角度摆动的振动 表达式分别为(用余弦函数表示): a (b) (a) (b) (c) (c) -64-
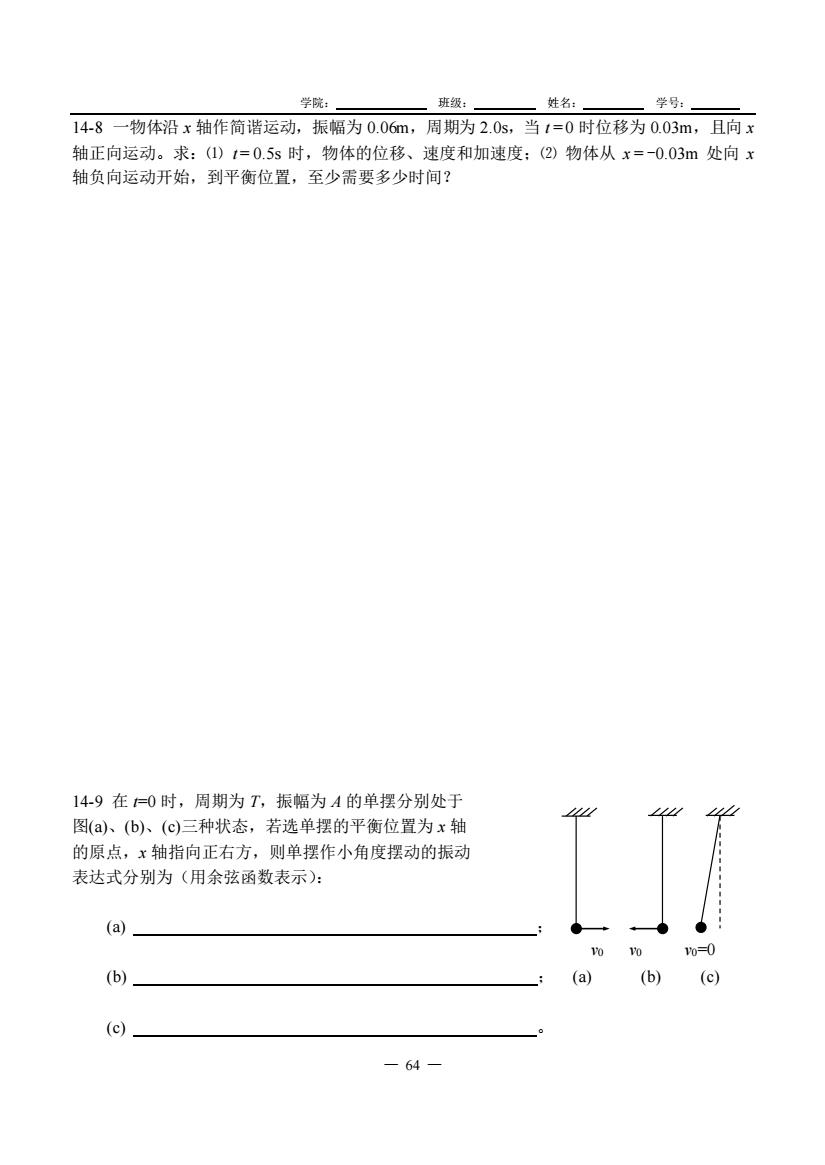
学院: 班级: 姓名: 学号: — 64 — 14-8 一物体沿 x 轴作简谐运动,振幅为 0.06m,周期为 2.0s,当 t = 0 时位移为 0.03m,且向 x 轴正向运动。求:⑴ t = 0.5s 时,物体的位移、速度和加速度;⑵ 物体从 x = -0.03m 处向 x 轴负向运动开始,到平衡位置,至少需要多少时间? 14-9 在 t=0 时,周期为 T,振幅为 A 的单摆分别处于 图(a)、(b)、(c)三种状态,若选单摆的平衡位置为 x 轴 的原点,x 轴指向正右方,则单摆作小角度摆动的振动 表达式分别为(用余弦函数表示): (a) ; (b) ; (a) (b) (c) (c) 。 v0 v0 v0=0

学院: 匮: 姓名: 学号: 14-10一轻质弹簧上端固定,下省挂一砝码。当砝码静止时,弹簧伸长001m。若将砝码上推, 使弹簧问到原长,然后放手,则砝玛上下振动 (1)证明砝码上下运动为诺椒动: (2)求此谐振动的振幅、角频率和频率: (3)若从放手时开始计时,求振动方程(设铅直向下为x轴正向)。 1411.一弹簧振子作简谐振动,总能量为E1,如果潜振动振幅增加为原来的两倍,重物的质量 也增为原来的两倍,则它的总能量E:受为】 A.E1/4 B.E1/2 C.2E1 D.4E -65-
学院: 班级: 姓名: 学号: — 65 — 14-10 一轻质弹簧上端固定,下端挂一砝码。当砝码静止时,弹簧伸长 0.01m。若将砝码上推, 使弹簧回到原长,然后放手,则砝码上下振动。 ⑴ 证明砝码上下运动为谐振动; ⑵ 求此谐振动的振幅、角频率和频率; ⑶ 若从放手时开始计时,求振动方程(设铅直向下为 x 轴正向)。 14-11 一弹簧振子作简谐振动,总能量为 E1,如果谐振动振幅增加为原来的两倍,重物的质量 也增为原来的两倍,则它的总能量 E1 变为[ ]。 A.E1/4 B.E1/2 C.2E1 D.4E1

学限 过名: 学号: 151己知一平面简谐波的波动方程为y=Ac0以(bM-),(h、d为正值常数),则此波的 ;波速w一 波长2 15-2某顷点作简谐振动。周期为25,振幅为0.06m,开始计时(1=0)。质点恰好处在负向最 大位移处。求:(I)该质点的椒动方程:(2)此振动以速度u=2s沿x轴正向传插时,形成的一 维简谐被的被动方程:(3)该波的波长。 15-3一平面被在媒质中以速度沿直线传搭,如图所示。己知在传播路径上的某点A的振动方月 程。()如以A点为坐标原点,写出被函数: (2)如以B点为坐标原点,写出被函数: 8m Sm n (3)写出C、D两点的振动方程: ()C点比D点的振动在相位上落后多少?C B D 一66
学院: 班级: 姓名: 学号: — 66 — 15-1 已知一平面简谐波的波动方程为 y = Acos(bt − dx) ,(b、d 为正值常数),则此波的 = ;波速 u = ;波长 = 。 15-2 某质点作简谐振动,周期为 2s,振幅为 0.06m,开始计时(t = 0),质点恰好处在负向最 大位移处。求:⑴该质点的振动方程;⑵此振动以速度 u = 2m/s 沿 x 轴正向传播时,形成的一 维简谐波的波动方程;⑶该波的波长。 15-3 一平面波在媒质中以速度沿直线传播,如图所示。已知在传播路径上的某点 A 的振动方 程。⑴ 如以 A 点为坐标原点,写出波函数; u ⑵ 如以 B 点为坐标原点,写出波函数; 8m 5m 9m ⑶ 写出 C、D 两点的振动方程; x ⑷ C 点比 D 点的振动在相位上落后多少? C B A D
学辰: 15-4平面简诺波以被速=0.50m·s1沿x轴负 y/m 向传播,1一2s时刻的波形如右图所示。求原点 .5 的运动方程。 10 2.0 I/m -67-
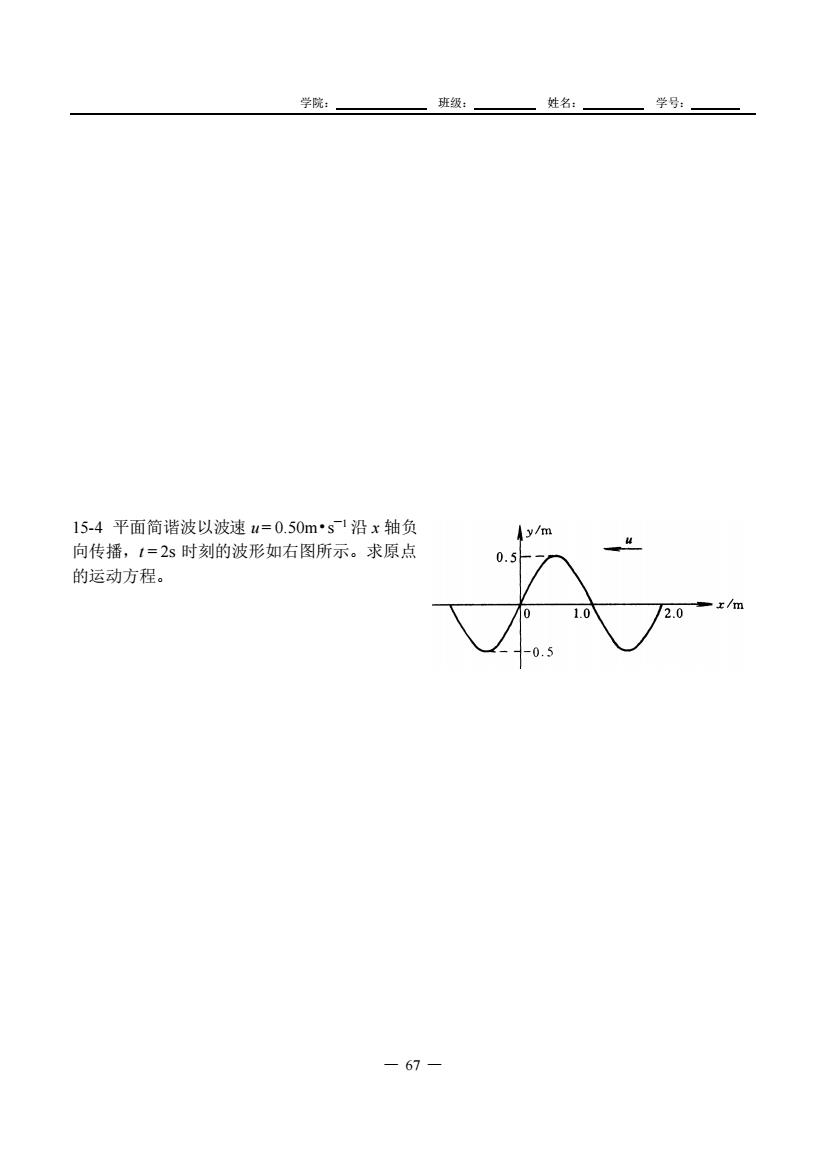
学院: 班级: 姓名: 学号: — 67 — 15-4 平面简谐波以波速 u = 0.50m•s —1 沿 x 轴负 向传播,t = 2s 时刻的波形如右图所示。求原点 的运动方程
学院: 透: 一姓名:一学 15.5一平面谐波,波长为12m,沿x轴负 y 向传播,右图所示为x=10m处质点的振动 0.4 曲线。求比被的被动方程。 0.2 3.0 15-6一平面简谐波。其振隔为A,顿率为V,波沿x轴正方向传播。设1=时刻被形如图15-1 所示,则x=0处质点振动方程为1。 A.y=Acos2()+ B.y=Aco2xVu-)+玉2] C.y=Acos[2 V(t-1o)-] D.y=Acos[2x(-)+] a)o. 图b) 图15-1 图15-2 15-7一·简谐被沿x轴正方向传播,1和两点处的振动曲线分别如图15-2中图(a)和图(b)所 示。已知>且和一1<2《2为波长),则x和点的相位比新点的相位潜后 一68-
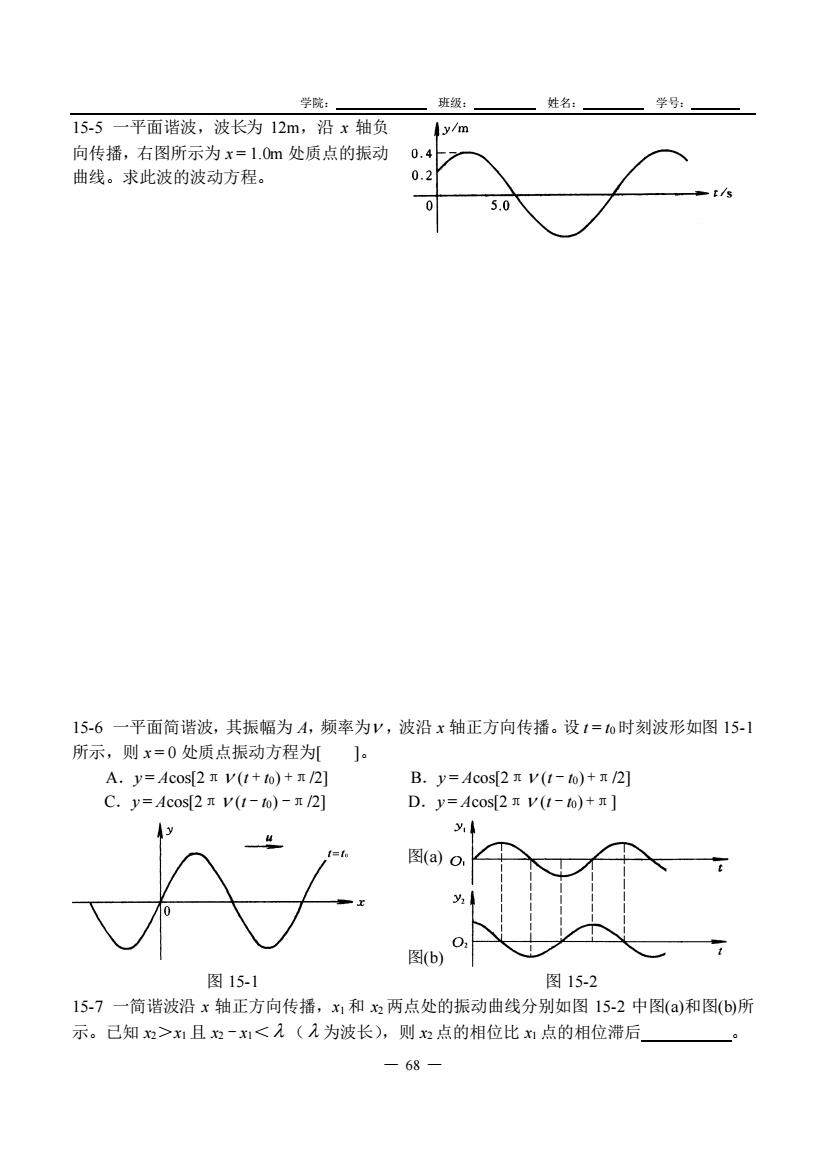
学院: 班级: 姓名: 学号: — 68 — 15-5 一平面谐波,波长为 12m,沿 x 轴负 向传播,右图所示为 x = 1.0m 处质点的振动 曲线。求此波的波动方程。 15-6 一平面简谐波,其振幅为 A,频率为 ,波沿 x 轴正方向传播。设 t = t0 时刻波形如图 15-1 所示,则 x = 0 处质点振动方程为[ ]。 A.y = Acos[2π (t + t0) +π/2] B.y = Acos[2π (t - t0) +π/2] C.y = Acos[2π (t - t0) -π/2] D.y = Acos[2π (t - t0) +π] 图 15-1 图 15-2 15-7 一简谐波沿 x 轴正方向传播,x1 和 x2 两点处的振动曲线分别如图 15-2 中图(a)和图(b)所 示。已知 x2>x1 且 x2 - x1< ( 为波长),则 x2 点的相位比 x1 点的相位滞后 。 图(a) 图(b)

学限 洗最: 姓名:学号: 15-8图示为平面简谐波在1=0时的 y/m 波形图,设此简诺波的频率为250Hz, 且处时图中点P的运动方向向上。 0.10 求:》该波的波动方程:☑在 0.05 x/m 距原点右侧7.5m处质点的运动方程与 1=0时该点的振动速度。 -0.05 —10.0m -0.10 159如图所示,两拔动方向相同的平面简诺波波源分别 位于A、B点。设它们相位相同,且频率V-30川2,被速 r=0.S0m·s。求点P处两列波的相位差。 3m 230 -0.07m —69
学院: 班级: 姓名: 学号: — 69 — 15-8 图示为平面简谐波在 t = 0 时的 波形图,设此简谐波的频率为 250Hz, 且此时图中点 P 的运动方向向上。 求:⑴ 该波的波动方程;⑵ 在 距原点右侧7.5m处质点的运动方程与 t = 0 时该点的振动速度。 15-9 如图所示,两振动方向相同的平面简谐波波源分别 位于 A、B 点。设它们相位相同,且频率 =30Hz,波速 u = 0.50m• s —1。求点 P 处两列波的相位差。 3m 30° 0.07m A B P

:一姓:一学号: 15-10如图所示,两相干波源分别在P、O两点, P Q R 它们发出顿率为V,波长为A,初相相同的两列相 干波,设PQ=3元2,R为2连线上的一点. 312 求:1)自P、Q发出的两列波在R处的相位整: 两波在R处干涉时的合振幅。 15-11如图所示,P点距波源S和S的距离分别为32 S1 和1013,入为两列波在介质中的波长,若P点的合 31 振幅总是极大值,则两波源应满足的条件是: S 1023 1512两相干波被源位于同一介质中的A、B两点, 如图所示,其振幅相等、顿丰皆为10OHz,B比A的 30m 相位超前。若A、B相距30.0m。被速为400m·s。 试求AB连线上因干涉而静止的各点的位置
学院: 班级: 姓名: 学号: — 70 — 15-10 如图所示,两相干波源分别在 P、Q 两点, P Q R 它们发出频率为 ,波长为 ,初相相同的两列相 干波,设 PQ = 3 /2,R 为 PQ 连线上的一点。 求:⑴ 自 P、Q 发出的两列波在 R 处的相位差; ⑵ 两波在 R 处干涉时的合振幅。 15-11 如图所示,P 点距波源 S1 和 S2 的距离分别为 3 S1 和 10 /3, 为两列波在介质中的波长,若 P 点的合 3 振幅总是极大值,则两波源应满足的条件是: P S2 10 /3 。 15-12 两相干波波源位于同一介质中的 A、B 两点, A B 如图所示。其振幅相等、频率皆为 100Hz,B 比 A 的 x 相位超前π。若 A、B 相距 30.0m,波速为 400 m• s —1。 试求 AB 连线上因干涉而静止的各点的位置。 3 /2 30m