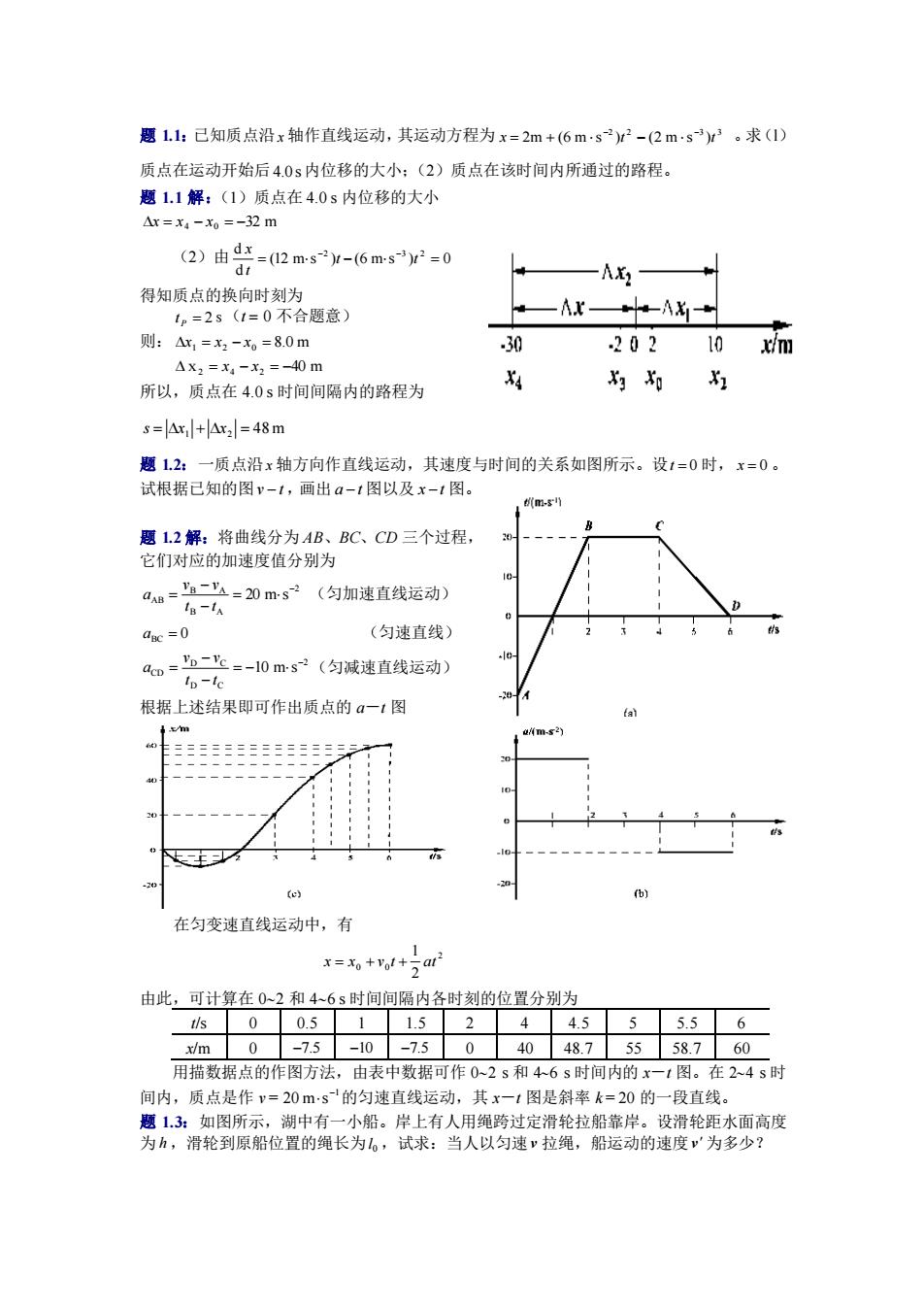
愿L1:已知质点沿x轴作直线适动,其运动方程为x=2m+6曲2-2m·sr。求(1) 质点在运动开始后40s内位移的大小:(2)质点在该时间内所通过的路程。 题1,1解,(1)质点在4.0s内位移的大小 △红=4-=-32m 《2)由-2m2y-6m2-0 AX: 得知质点的换向时划为 5,=2s(1=0不合题意) —x中A 则:邮,=-无=8.0m 30 202 10 x'm 4x:=名-名=0m 所以,质点在4.0s时间间隔内的路程为 s=Ar+Ar:=48m 题12:一质点沿x轴方向作直线运动,其速度与时间的关系如图所示。设í=0时,x=0。 试根据已知的图r-f,画出a-r图以及x一:图, 间的-41 题L2解:将曲线分为AB、BC,CD三个过程, 它们对应的加速度值分别为 m=n-=20mg3(匀加速直线运动) In-fa r=0 (匀速直线) m=h二=-10ms(匀减速直线运动) Io"le 根据上述结果即可作出质点的?一!图 在匀变速直线运动中。有 =+W+行 由此:可计算在02和46s时间阿隔内各时刻的位置分别为 0051152☐4455556 m0-7.5-10-7.50404875558760 用描数据点的作图方法,由表中数据可作0-2s和46s时间内的x一(图。在243时 间内,质点是作?=20ms的匀速直线运动。其x一1图是斜率k=20的一段直线。 恩13多如图所示,湖中有一小船。岸上有人用绳跨过定滑轮拉船靠岸。设滑轮距水面高度 为,滑轮到原船位置的绳长为,试求:当人以匀速拉绳,船运动的速度'为多少?
题 1.1:已知质点沿 x 轴作直线运动,其运动方程为 2 2 3 3 x 2m (6 m s )t (2 m s )t − − = + − 。求(l) 质点在运动开始后 4.0 s 内位移的大小;(2)质点在该时间内所通过的路程。 题 1.1 解:(1)质点在 4.0 s 内位移的大小 x = x4 − x0 = −32 m (2)由 (12 m s ) (6 m s ) 0 d d 2 3 2 = − = − − t t t x 得知质点的换向时刻为 tP = 2s (t = 0 不合题意) 则: x1 = x2 − x0 = 8.0 m x2 = x4 − x2 = −40 m 所以,质点在 4.0 s 时间间隔内的路程为 s = x1 + x2 = 48 m 题 1.2:一质点沿 x 轴方向作直线运动,其速度与时间的关系如图所示。设 t = 0 时, x = 0 。 试根据已知的图 v − t ,画出 a −t 图以及 x −t 图。 题 1.2 解:将曲线分为 AB、BC、CD 三个过程, 它们对应的加速度值分别为 2 B A B A AB 20 m s − = − − = t t v v a (匀加速直线运动) aBC = 0 (匀速直线) 2 D C D C CD 10 m s − = − − − = t t v v a (匀减速直线运动) 根据上述结果即可作出质点的 a-t 图 在匀变速直线运动中,有 2 0 0 2 1 x = x + v t + at 由此,可计算在 02 和 46 s 时间间隔内各时刻的位置分别为 t/s 0 0.5 1 1.5 2 4 4.5 5 5.5 6 x/m 0 −7.5 −10 −7.5 0 40 48.7 55 58.7 60 用描数据点的作图方法,由表中数据可作 02 s 和 46 s 时间内的 x-t 图。在 24 s 时 间内,质点是作 v = 20 1 m s − 的匀速直线运动,其 x-t 图是斜率 k = 20 的一段直线。 题 1.3:如图所示,湖中有一小船。岸上有人用绳跨过定滑轮拉船靠岸。设滑轮距水面高度 为 h ,滑轮到原船位置的绳长为 0 l ,试求:当人以匀速 v 拉绳,船运动的速度 v 为多少?

题13解1:取如图所示的直角坐标系,船的运动方程为 r)-xr+) 静的运动速度为 d山d山 d山 而收绳的速率v。一少,且因r一一W故 1}w 题13解2:取图所示的极坐州:,则 rt。山 de,dr +r e+F9 山山 是船的径向速度。一巴气是船的横向速度。西 d 业是收绳的速率,由于船速,与径向速度之间夹角 位B,所以 Y--- 由此可知,收绳的速率只是船速沿绳方向的分量。 恩14:一升降机以加速度12m-s上升,当上升速度为2.4ms时,有一螺维白升降机 的天花板上松殿,天花板与升降机的底面相距24m:计算:(1)螺丝从天花板落到底面所 需要的时间:(2)螺纶相对升降机外固定柱子的下降距离。 题1.4解1:)以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为 =wr 为=h+- 当螺丝落至底面时,有另“为,即 +2r-h+-r .-005s + (2)螺丝相对升降机外国定柱子下降的距离为 d--为-W+58-076m 恩L4解2上()以升降机为参考系,此时,螺纶相对它的加速度大小。=g+@,螺丝落至底 面时,有
题 1.3 解 1:取如图所示的直角坐标系,船的运动方程为 r(t) = x(t)i + (−h)j 船的运动速度为 ( ) i i i r v t r r h r h t t x t t d d 1 d d d d d d 1/ 2 2 2 2 2 − = = = − = − 而收绳的速率 t r v d d = − ,且因 r = l −vt 0 ,故 ( ) v i 1 / 2 2 0 2 1 − − = − − l vt h v 题 1.3 解 2:取图所示的极坐标(r,),则 r θ r r d d d d d d d d d d e e e e r v t r t r t r t r t = = + = + r d d e t r 是船的径向速度, θ d d e t r 是船的横向速度,而 t r d d 是收绳的速率。由于船速 v与径向速度之间夹角 位 ,所以 ( ) v i i 1 / 2 2 0 2 1 cos − − = − = − − l vt h v v 由此可知,收绳的速率只是船速沿绳方向的分量。 题 1.4:一升降机以加速度 2 1.22 m s − 上升,当上升速度为 2 2.44 m s − 时,有一螺丝自升降机 的天花板上松脱,天花板与升降机的底面相距 2.74m 。计算:(1)螺丝从天花板落到底面所 需要的时间;(2)螺丝相对升降机外固定柱子的下降距离。 题 1.4 解 1: (1)以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为 2 1 0 2 1 y = v t + at 2 2 0 2 1 y = h + v t − gt 当螺丝落至底面时,有 1 2 y = y ,即 2 0 2 0 2 1 2 1 v t + at = h + v t − gt 0.705 s 2 = + = g a h t (2)螺丝相对升降机外固定柱子下降的距离为 0.716 m 2 1 2 d = h − y2 = −v0 t + gt = 题 1.4 解 2:(1)以升降机为参考系,此时,螺丝相对它的加速度大小 a = g + a ,螺丝落至底 面时,有

0-8-a 「2h ,=0705s (2)由于升降机在,时间内上升的高度为 von 则d=h-=0.716m 题15:一质点P沿率径R=300m的周作匀速率运动,运动一周所需时间为2003,设:=0 时,质点位于O点。按图中所示O坐标系,求(1)质点P在任意时刻的位矢:(2)5s时 的速度和加速度。 恩L5解:如图所示,在Oy坐标系中,因0-三 ,则质点P 的参数方程为 r-Ran停4y-Ram 坐标变换后,在Oy坐标系中有 y=+%=-Rs经1+R 2x x=x'=Rsm 则质点P的位矢方程为 =Rsm亭i+(a亭+ =(3 m)smno s]i+(3m-coso.1s 5s时的速度和加速度分别为 r=业=Rcs2i+Rsj=3rm-g T T T d'r 题16:一质点自原点开始沿抛物线y-缸运动,它在O伍轴上的分速度为一恒量,其值为 ,=40m。,求质点位于x一20m处的速度和加速度, 题16解:因,-40ms为一常数,故a-0.当1-0时,x-0.由.-业积分可得 d x=F() 又由质点的附物线方程,有 y-hrv (2) 由y方向的运动方程可得该方向的速度和加速度分量分别为
( ) 2 2 1 0 = h − g + a t 0.705 s 2 = + = g a h t (2)由于升降机在 t 时间内上升的高度为 2 0 2 1 h = v t + at 则 d = h − h = 0.716 m 题 1.5:一质点 P 沿半径 R = 3.00m 的圆周作匀速率运动,运动一周所需时间为 20.0 s ,设 t = 0 时,质点位于 O 点。按图中所示 Oxy 坐标系,求(1)质点 P 在任意时刻的位矢;(2) 5 s 时 的速度和加速度。 题 1.5 解:如图所示,在 Oxy坐标系中,因 t T 2 = ,则质点 P 的参数方程为 t T t y R T x R 2 , cos 2 = sin = − 坐标变换后,在 Oxy 坐标系中有 t R T t y y y R T x = x = R = + = − + 2 , cos 2 sin 0 则质点 P 的位矢方程为 ( ) ( ) i ( ) ( ) j r i j t t t R T t R T R 1 1 3 m sin 0.1 s 3 m 1 cos 0.1 s 2 cos 2 sin − − = + − = + − + 5 s 时的速度和加速度分别为 i j ( )j r v 1 0.3 m s 2 sin 2 2 cos 2 d d − = = + = t T T t R T T R t i tj ( )i r a 2 2 2 2 2 2 0.03 m s 2 cos 2 2 sin 2 d d − = − + = = − T T t R T T R t 题 1.6:一质点自原点开始沿抛物线 2 y = bx 运动,它在 Ox 轴上的分速度为一恒量,其值为 1 4.0 m s − = x v ,求质点位于 x = 2.0 m 处的速度和加速度。 题 1.6 解:因 vx = 4.0 1 m s − 为一常数,故 ax = 0。当 t = 0 时,x = 0,由 t x v d d x = 积分可得 x v t = x (1) 又由质点的抛物线方程,有 ( ) 2 x 2 y = bx = b v t (2) 由 y 方向的运动方程可得该方向的速度和加速度分量分别为

5-告-2的 4-当-2诚四 当质点位于x=2.0m时,由上述各式可得 P=1+¥,/-h0msh+80ms/ a-ai+aj-016m.sj 题17:质点在0gy平面内运动,其运动方程为r=260曲·%'M+90m-2D曲·%U: 求:(1)质点的轨迹方程:(2》在1-1.0s到1:一200s时间内的平均速度:(2)1-1.00s时 的速度及切向和法向加速度。 题1,7解:(1)由参数方程 x-6200 m.s)y-19.0m-(2.00 m.s) 清去,得质点的轨迹方程 y=l9.0m-050m)x2 (2)在1=1.00s到2=200s时间内的平均速度 ==-5=00ms)i-60ms)万 m-4 (3)质点在任意时刻的速度和加速度分别为 0)-.+-+业-0ms1-kmms) 0普÷=mm de= 则1=1.00s时的速度 ra.=.00msi-4mm-8)i 切向和法向加速度分别为 -告-反写k-6gmk a =Ja-ae =(1.79m-s)e 恩1,8质点的运动方程为x=(-0m-sr+(30m-s2和y=-l5msM-(20ms2r2, 试求:(1)初速度的大小和方向:(2)加速度的大小和方向 题18解:(1)建度分量式为 =业=-10m-g+0mg d山 =5ms-0ms ,d 当1=0时,m--10ms,%y=15ms,则初速度大小为
bv t t y v 2 y 2 x d d = = (3) 2 x 2 y 2 d d bv t y a 2 = = (4) 当质点位于 x = 2.0 m 时,由上述各式可得 v i j ( )i ( ) j 1 1 x y 4.0 m s 8.0m s − − = v + v = + a i j ( ) j 2 x y 16 m s − = a + a = 题 1.7:质点在 Oxy 平面内运动,其运动方程为 r (2.00 m s ) i [19.0 m (2.00 m s ) ]j 1 2 2 t t − − = + − 。 求:(1)质点的轨迹方程;(2)在 1.00 s t 1 = 到 2.00 s t 2 = 时间内的平均速度;(2) 1.00 s t 1 = 时 的速度及切向和法向加速度。 题 1.7 解:(1)由参数方程 ( ) ( ) 1 2 2 x 2.00 m s t, y 19.0 m 2.00 m s t − − = = − 消去 t 得质点的轨迹方程 ( ) 1 2 y 19.0 m 0.50 m x − = − (2)在 t 1 =1.00 s 到 t 2 = 2.00 s 时间内的平均速度 ( )i ( ) j r r r v 1 1 2 1 2 1 2.00 m s 6.00 m s − − = − − − = = t t t (3)质点在任意时刻的速度和加速度分别为 v( ) i j i j ( )i ( ) t j t y t x t v v 1 2 x 2.00 m s 4.00 m s d d d d − − = + = + = − a( ) i j ( )j 2 2 2 2 2 4.00 m s d d d d − = + = t y t x t 则 t1 = 1.00 s 时的速度 v( ) ( )i ( ) j 1 1 t 1 s 2.00 m s 4.00 m s − − = t = − 切向和法向加速度分别为 ( ) ( ) t 2 t 2 t t 1 s t x y 3.58 m s d d d d a e v e e 2 − = = = + v = t t v ( ) n 2 n 2 t 2 n a e 1.79m s e − = a − a = 题 1.8:质点的运动方程为 1 2 2 x ( 10 m s )t (30 m s )t − − = − + 和 1 2 2 y ( 15 m s )t (20 m s )t − − = − − , 试求:(1)初速度的大小和方向;(2)加速度的大小和方向。 题 1.8 解:(1)速度分量式为 ( )t t x v 1 2 x 10 m s 60 m s d d − − = = − + ( )t t y v 1 2 y 15 m s 40 m s d d − − = = − 当 t = 0 时,v0x= −10 1 m s − ,v0y = 15 1 m s − ,则初速度大小为

6=+=80mg 设和与x轴的夹角为a。则 tga a=12341 (2)加速度的分量式为 告=0m8-告=0m d山 则加速度的大小为 a=匠+g=2.1ms 设a与x轴的夹角为?则 w经-月 B=3341或逆19 愿L:一质点具有恒定加速度a=6mM+4曲川,在1=0时,其速度为零,位置矢 量-(DmM:求:(1)在任意时刻的速度和位置失量:(2)质点在0g平面上的轨迹方程。 并画出轨迹的示意图。 题1.9解:由如速度定义式,根据初始条件=0时=0,积分可得 =j后=。6msi+4ms 学=(6ms3)i+(4m-s3)1i 又由一出及初始条作t0时,。·00m以.积分可得 =后w=瓜6msi+4msjm F-0m+3m-%y1i+2ms)广U 由上述结果可得质点运动方程的分量式,即 本=10+6曲g) 3g2r-200 y-km.s) 0 消去参量,可得运动的轨迹方程 3y=2x-20m 这是一个直线方程,直线斜率★=史=a= 方·《=3产4打。轨迹如图所示。 思11h飞机以10m~%的速度沿水平直线飞行,在离地面高为100m时,驾驶员要把物品 投到前方某一地面目标处。问:(1)此时目标在飞机下方前多近?(2)投故物品时,驾驶
2 1 0y 2 0 0x 18.0 m s − v = v + v = 设 v0 与 x 轴的夹角为,则 2 3 tg 0y 0x = = − v v =123 41 (2)加速度的分量式为 y 2 y x 2 x 40m s d d 60 m s , d d − − = = = = − t v a t v a 则加速度的大小为 2 2 y 2 x 72.1m s − a = a + a = 设 a 与 x 轴的夹角为,则 3 2 tg x y = = − a a = −33 41( 326 19) 或 题 1.9:一质点具有恒定加速度 a (6 m s )i (4 m s ) j −2 −2 = + ,在 t = 0 时,其速度为零,位置矢 量 r (10 m)i 0 = 。求:(1)在任意时刻的速度和位置矢量;(2)质点在 Oxy 平面上的轨迹方程, 并画出轨迹的示意图。 题 1.9 解:由加速度定义式,根据初始条件 t0 = 0 时 v0 = 0,积分可得 t t v t t d d [(6 m s (4 m s ) ]d 0 2 2 0 0 − − v = a = )i + j v (6 m s ) ti (4 m s ) t j −2 −2 = + 又由 dt dr v = 及初始条件 t = 0 时,r0 = (10 m)i,积分可得 t t t t r t t d d [(6 m s ) (4 m s ) ]d 0 2 2 0 0 − − r = v = i + j r [10 m (3 m s ) ] i [(2 m s ) ]j 2 2 2 2 t t − − = + + 由上述结果可得质点运动方程的分量式,即 ( ) 2 2 x 10 m 3 m s t − = + ( ) 2 2 y 2 m s t − = 消去参数 t,可得运动的轨迹方程 3y = 2x−20m 这是一个直线方程,直线斜率 3 2 tan d d = = = x y k , = 33 41 。轨迹如图所示。 题 1.10:飞机以 1 100 m s − 的速度沿水平直线飞行,在离地面高为 100m 时,驾驶员要把物品 投到前方某一地面目标处。问:(1)此时目标在飞机下方前多远?(2)投放物品时,驾驶

员看目标的视线和水平线成何角度?(3)物品投出20s后,它的法向加速度和切向加速 度各为多少? 题L,10解()取如图所示的坐标,物品下落时在水平和经直方向的运动方程分别为 =y=38 飞机水平飞行速度v-00ms。飞机离地面的 高度y=100m,由上述两式可得目标在飞机正 下方前的距离 2y =452m (2)视线和水平线的夹角为 0-ag子-25 (3)在任意时刻物品的速度与水平轴的夹角为 7777777777777777777777 a=arg之=g型 取自然坐标,物品在抛出2s时,重力加速度的切向分量与法白分量分别为 民,=gs的行=累s -18粥m2 ¥ --8 cos arctg型 -962ms 题1.11:一足球运动员在正对球门前250m处以00m的初速率罚任意球,已知球门高 为344m,若要在垂直于球门的竖直平面内将足球直接蜀进球门,问他应在与地而成什么角 度的范围内锡出足球?(是球可视为质点) 题1,11解:取图示坐标系O炒,由运动方程 1 =6osJ=Wsm0-五8 消去:得轨迹方程 y=ngo-8+igoh 2w2 以x=25.0m,v=20.0ms及3442y20代入后,可解得 71.112a≥69.9r° 27.922a218.8r 如何理解上述角度得范围? 在初速度一定的条件下,球击中球门底线或球门上缘都将对应有两个不同的投射倾角 (如图所示)。如果以升>71.11威9<18.8W现出足球,都将因财程不足而不能直接射入球门1 由于球门高度的限制.8角也并能取71.11*与18之间的任何值植,当领角取值为2792< 0<6992时,现出的足球将越过门锋而离去,这时也球不能射入球门。因此可取的角度范 用只能是解中的结果。 恩112:设从某一点O以同样的速率,沿着月一竖直面内各个不月方向同时剩出几个物体 试证:在任意时刻,这几个物体总是散落在某个圆周上。 题1,2证:取物体抛出点为坐标原点,建立如图所示的坐标系。物体运动的参数方程为
员看目标的视线和水平线成何角度?(3)物品投出 2.00s 后,它的法向加速度和切向加速 度各为多少? 题 1.10 解:(1)取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为 2 2 1 x = vt, y = gt 飞机水平飞行速度 v =100 1 m s − ,飞机离地面的 高度 y = 100 m,由上述两式可得目标在飞机正 下方前的距离 452 m 2 = = g y x v (2)视线和水平线的夹角为 = arctg = 12.5 x y (3)在任意时刻物品的速度与水平轴的夹角为 v gt v v x y = arctg = arctg 取自然坐标,物品在抛出 2 s 时,重力加速度的切向分量与法向分量分别为 2 sin sin arctg 1.88 m s − = = = v gt at g g 2 cos cos arctg 9.62 m s − = = = v gt an g g 题 1.11:一足球运动员在正对球门前 25.0 m 处以 1 20.0 m s − 的初速率罚任意球,已知球门高 为 3.44m 。若要在垂直于球门的竖直平面内将足球直接踢进球门,问他应在与地面成什么角 度的范围内踢出足球?(足球可视为质点) 题 1.11 解:取图示坐标系 Oxy,由运动方程 2 2 1 x = vt cos, y = vtsin − gt 消去 t 得轨迹方程 ( ) 2 2 2 1 tg 2 tg x v g y = x − + 以 x = 25.0 m,v = 20.0 1 m s − 及 3.44 y 0 代入后,可解得 71.11º 69.92º 27.92º 18.89º 如何理解上述角度得范围? 在初速度一定的条件下,球击中球门底线或球门上缘都将对应有两个不同的投射倾角 (如图所示)。如果以 71.11或 <18.89踢出足球,都将因射程不足而不能直接射入球门; 由于球门高度的限制, 角也并非能取 71.11与 18.89之间的任何值。当倾角取值为 27.92 < < 69.92时,踢出的足球将越过门缘而离去,这时也球不能射入球门。因此可取的角度范 围只能是解中的结果。 题 1.12:设从某一点 O 以同样的速率,沿着同一竖直面内各个不同方向同时抛出几个物体。 试证:在任意时刻,这几个物体总是散落在某个圆周上。 题 1.12 证:取物体抛出点为坐标原点,建立如图所示的坐标系。物体运动的参数方程为

x=Vetc0s0.y=Vatsin0-Tgr 清去式中参数0,得任意时刻的轨迹方程为 j 这是一个以-宁门为圆心,W为半径的圆方到如图所 示),它代表着所有物体在任意时刻:的位置。 题L13:一质点在半径为R的圆周上以恒定的速率运动,质点由位置A运动到位置B,O4 和O沿所对的圈心角为A8。 (1)试证位置A和B之间的平均加速度为可=,√21-%△m2R3 (2)当10分别等于9心、30、1心和1r时,平均如速度各为多少?并对结果加以讨论: 题1.13解:)由图可看到y=2-书,故 Ari+vi-2v,v:COs40 -Ty201-co4B) 公 Ar=A5-RA0 所以石.l侧-2-s0 RA日 (2)将A0-0,3,10,r分别代入上式,得 a003 R可*0886 *087上 上述结果表明:当△8→0时,匀速率圈周运动的平均如速 度趋于一极限值,该值即为法向加速度 R· 愿14一质点沿半经为R的阀周按规律-W-三运动,。、b都是常量。)求:时 刻的总如速度:(2)1为何值时总加速度在数值上等于s?(3)当加速度达到b时,质点已 沿圆周运行了多少圈? 题1,14解:(1)质点作圆周运动的速率为 d山 -。-bM 其如速度的切向分量和法向分量分别为 4普4后 故加速度的大小为 后+可.护+伦-时 R 其方白与切线之间的夹角为
2 0 0 2 1 x = v t cos, y = v tsin − gt 消去式中参数 ,得任意时刻的轨迹方程为 ( ) 2 0 2 2 2 2 1 x y gt = v t + + 这是一个以 − 2 2 1 0, gt 为圆心、v0t 为半径的圆方程(如图所 示),它代表着所有物体在任意时刻 t 的位置。 题 1.13:一质点在半径为 R 的圆周上以恒定的速率运动,质点由位置 A 运动到位置 B ,OA 和 OB 所对的圆心角为 。 (1)试证位置 A 和 B 之间的平均加速度为 2(1 cos ) /( ) 2 a = − v R ; (2)当 分别等于 90 、 30 、 10 和 1 时,平均加速度各为多少?并对结果加以讨论。 题 1.13 解:(1)由图可看到 2 1 v = v − v ,故 = + −2 cos = 2(1−cos ) 1 2 2 2 2 1 v v v v v v 而 v R v s t = = 所以 ( ) = − = R v t v a 2 2 1 cos (2)将 = 90 ,30 ,10 ,1 分别代入上式,得 R v a R v a R v a R v a 2 4 2 3 2 2 2 1 0.900 3 , 0.988 6 , 0.998 7 , 1.000 上述结果表明:当 → 0 时,匀速率圆周运动的平均加速 度趋于一极限值,该值即为法向加速度 R v 2 。 题 1.14:一质点沿半径为 R 的圆周按规律 2 0 2 1 s = v t − bt 运动, 0 v 、b 都是常量。(1)求 t 时 刻的总加速度;(2) t 为何值时总加速度在数值上等于 b ?(3)当加速度达到 b 时,质点已 沿圆周运行了多少圈? 题 1.14 解:(1)质点作圆周运动的速率为 v bt t s v = = 0 − d d 其加速度的切向分量和法向分量分别为 ( ) R v bt R v b a t s a 2 2 0 2 n 2 t , d d − = = − = = 故加速度的大小为 ( ) R R b v bt a a a 4 0 2 2 2 t 2 n + − = + = 其方向与切线之间的夹角为

0=e是=g6-】 2要使H-点由R一-A可得 房 (3)从1=0开始到1=/b时,质点经过的路程为 6=活 因此质点运行的圈数为 题L15障位是一素表面覆盖一层信息记录物质的塑性司片。若障世可读部分的内外半径分 别为2.0©m和58船cm:在回放时,嚎盘被以恒定的线速度由内向外沿螺黎扫描线(阿基米 德螺线)进行扫城.(1)若开始时读写模盘的角速度为00ds,则速完时的角速度为多 少?(2)若螺炭线的间距为1.60m,求扫描线的总长度和回成时间。 题115分析,阿基米德螺线是一等速的螺旋线,在极坐标下,它的参数方程可表示为 ?=+48,式中r为极径,心为初始极径。为极角。a为常量。它的图线是等间距的。当 间距为d时,常量a-d2m。因此,扫描线的总长度可通过积分s=∫同0得到。 解:()由于线速度恒定,则由¥=,可得仙,=5·故暖盘读完时的角速度为 @2=5/5=21.6d-s 2)在可读范围内,螺旋线转过的极角8=23-r)/d,故扫描线的总长度为 -j8- ,是g.出-d58x0'm d 藻盘目放的时间为 t■3/p=410x101s年1.15h 本题在求扫描线的总长度时,也可采用平均周长的计算方法,即 5=2m55=2x5*5-5=5.38×0'm 2 题116:地面上垂直竖立一高200m的旗杆,已知正午时分太购在旗杆的正上方,求在下午 2时正,杆顶在地面上的影子的度的大小。在问时划杆影将钟展至长2D0m? 题1.16解:设太阳光线对地转动的角速度为,从正午时分开始计时,则杆的影长为x=g: 下午2时整,杆美在地面上影子的速度大小为 ,-血。n-194×10m dr cos'er 当杆长等于影长时,即=,则 ,三=元=3x60×60 即为下午3时整
( ) − = = − Rb v bt a a 2 0 t n arctg arctg (2)要使 a = b, 由 R b (v bt) b R + − = 1 2 2 4 可得 b v t 0 = (3)从 t = 0 开始到 t = v0/b 时,质点经过的路程为 b v s s s 2 2 0 = t − 0 = 因此质点运行的圈数为 bR v R s n 2 4 2 0 = = 题 1.15:碟盘是一张表面覆盖一层信息记录物质的塑性圆片。若碟盘可读部分的内外半径分 别为 2.50 cm 和 5.80 cm 。在回放时,碟盘被以恒定的线速度由内向外沿螺旋扫描线(阿基米 德螺线)进行扫描。(1)若开始时读写碟盘的角速度为 1 50.0 rad s − ,则读完时的角速度为多 少?(2)若螺旋线的间距为 1.60μm ,求扫描线的总长度和回放时间。 题 1.15 分析:阿基米德螺线是一等速的螺旋线,在极坐标下,它的参数方程可表示为 r = r0 + a ,式中 r 为极径,r0 为初始极径,为极角,a 为常量。它的图线是等间距的,当 间距为 d 时,常量 a = d/2。因此,扫描线的总长度可通过积分 s = rd 得到。 解:()由于线速度恒定,则由 v = r ,可得 1 1 2 2 r = r ,故碟盘读完时的角速度为 1 2 1 1 2 / 21.6 rad s − = r r = ()在可读范围内,螺旋线转过的极角 = 2 (r2 − r1 )/ d ,故扫描线的总长度为 ( ) ( ) = − = = = + − d 5.38 10 m 2 d 3 2 1 2 2 2 / 0 1 2 1 d d r r s r r r r d 碟盘回放的时间为 / 4.10 10 s 1.15 h 3 t = s v = 本题在求扫描线的总长度时,也可采用平均周长的计算方法,即 5.38 10 m 2 2 2 2 2 1 2 1 2 1 3 = + − = + = d r r r r r r s n 题 1.16:地面上垂直竖立一高 20.0 m 的旗杆,已知正午时分太阳在旗杆的正上方,求在下午 2 时正,杆顶在地面上的影子的速度的大小。在何时刻杆影将伸展至长 20.0 m ? 题 1.16解:设太阳光线对地转动的角速度为,从正午时分开始计时,则杆的影长为s = htgt, 下午 2 时整,杆顶在地面上影子的速度大小为 3 1 2 1.94 10 m s d cos d − − = = = t h t s v 当杆长等于影长时,即 s = h,则 3 60 60 s 4 arctg 1 = = = h s t 即为下午 3 时整

题1,1⑦:一半径为050m的飞轮在启动时的复时间内,其角速度与时间的平方成正比。在 t=20s时测得轮缘一点速度值为4.0ms。求,(1)该轮在-0.5s的角速度。轮锋一点 的切向加速度和总加速度:(2)该点在20s内所转过的角度。 题L.17解:因成=V,由题意移比户得比例系数 所以9=)-巨adsr 则:0.5s时的角速度、角如速度和切向如速度分别为 o-md.s)r -05rad-s- a=e=卡ds)r=20dg 8,=成=10曲g 总加速度 a=属+息。=a,+@8e. a=Va成}+e2=10lms 在205内该点转过的角度 0--广ow-ea-so--传ad-53a 思118:一质点在半径为010m的圆周上运动,其角位置为8-2d+4ds1y。(1》求 在/=2.0时质点的法向加速度和切向加速度,(2)当切向加速度的大小恰等于总加连度大 小的一半时,0值为多少?(3)‘为多少时,法向加速度和切向加速度的值相等 题L1s解(油于0-2d:6ad,则角速度a-出-2时s,在1-2时, 法向加速度和切向加速度的数植分别为 .a.■m2=20×02mg2 la=r如=40ms 回当a=反+云时.有城=.即 4mds川-2dsr] 1=2万=029s 此时刻的角位置为 @-2 md+4 rad-s)-3.15 md
题 1.17:一半径为 0.50m 的飞轮在启动时的短时间内,其角速度与时间的平方成正比。在 t = 2.0 s 时测得轮缘一点速度值为 1 4.0 m s − 。求:(1)该轮在 t = 0.5 s 的角速度,轮缘一点 的切向加速度和总加速度;(2)该点在 2.0 s 内所转过的角度。 题 1.17 解:因 R = v ,由题意 2 t 得比例系数 3 2 2 2 rad s − = = = Rt v t k 所以 ( ) ( ) 3 2 t 2 rad s t − = = 则 t=0.5 s 时的角速度、角加速度和切向加速度分别为 ( ) 3 2 1 2 rad s 0.5 rad s − − = t = ( ) 3 2 4 rad s 2.0 rad s d d - = = = − t t 2 1.0 m - a R s t = = 总加速度 n 2 t n t a = a + a =Re + Re ( ) ( ) 2 2 2 2 1.01 m s − a = R + R = 在 2.0 s 内该点转过的角度 ( ) rad s 5.33 rad 3 2 d 2 rad s d 3 3 2 s 0 3 2 2 0 0 = − = = = − − t t t t s 题 1.18:一质点在半径为 0.10m 的圆周上运动,其角位置为 3 3 2 rad (4 rad s )t − = + 。(1)求 在 t = 2.0 s 时质点的法向加速度和切向加速度。(2)当切向加速度的大小恰等于总加速度大 小的一半时, 值为多少?(3) t 为多少时,法向加速度和切向加速度的值相等? 题 1.18 解: (1)由于 ( ) 3 3 2 rad 4 rad s t − = + ,则角速度 ( ) 3 2 12 rad s d d t t − = = ,在 t = 2 s 时, 法向加速度和切向加速度的数值分别为 2 2 2 n t 2 s 2.30 10 m s − = a = r = 2 t t 2s 4.80 m s d d − = = = t a r (2)当 2 t 2 t n 2 1 2 a a a a = = + 时,有 2 n 2 3at = a ,即 ( ) ( ) 3 2 2 3 2 4 3 r 24 rad s t r 12 rad s t − − = s 0.29 s 2 3 1 t = = 此时刻的角位置为 2 rad (4 rad s ) 3.15 rad 3 3 = + = − t

(3)要使a。=a,则有 r2ads)r}-4ads)g 1=0.55s 题1.19:一无风的下雨天,一列火车以y=20.0ms1的速度匀速前进,在车内的旅客看见 玻璃窗外的雨滴和垂线成75角下降,求雨滴下落的速度,:。(设下降的雨滴作匀速运动) 题1.19分析:这是一个相对运动的问。设雨滴为研究对象,地面为静止参考系S,火车 为动参考系$”。为S相对S的速度,之为雨滴相对S的速度,利用相对运动速度的关系 即可解。 解:以地面为参考系,火车相对地面运动的速度 关系为=+,于是 8=56ms 题1.20:设有一架飞机从A处向东飞到B处,然后又向西飞回到A处,飞机相对空气的速 为·,而空相对地面的速率 R间的距离为 ,飞机相对空气的速率 保持不 变。(1)假定空气是静止的(即M=0 试证来回飞机飞行时间为,=21 (2)假定空气的速度向东,试证来回飞行时间为1,=,0-): (3)假定空气的速度向北,试证来国飞行时间为,=1,0-”)。 题1.20证:由相对速度的矢量关系='+,有 (1)空气是静止的,即“=0,则往返时,飞机相对地面的 飞行速度v就等于相对空气的速度',故飞行往返所需时 一B 间为 6+h+- (2)按题意,当飞机向东时,风速与飞机相对与空气的速度同向:而飞机由东返回时,两者 刚好反向。这时,飞机在往返飞行时,相对于地面的速度值分别为v=v+u和v=V-M。 因此,飞行往返所需时间为 。别 (3)当空气速度向北时,飞机相对地面的飞行速度的大小由 v=v+m可得为=2-,则飞机往返所需时间为 =- 题1.21:如图所示 汽车在雨中沿直线行使,其速率为,下落雨滴的速度方向偏于竖 直方向之前角,速率为,若车后有一长方形物体,问车速,为多大时,此物体正好不会
(3)要使 an = at ,则有 r( )t r( )t 3 2 2 3 12 rad s 24 rad s − − = t = 0.55 s 题 1.19:一无风的下雨天,一列火车以 1 1 20.0 m s − v = 的速度匀速前进,在车内的旅客看见 玻璃窗外的雨滴和垂线成 75 角下降,求雨滴下落的速度 2 v 。(设下降的雨滴作匀速运动) 题 1.19 分析:这是一个相对运动的问题。设雨滴为研究对象,地面为静止参考系 S,火车 为动参考系 S。v1 为 S相对 S 的速度,v2 为雨滴相对 S 的速度,利用相对运动速度的关系 即可解。 解:以地面为参考系,火车相对地面运动的速度 为 v1,雨滴相对地面竖直下落的速度为 v2,旅客 看到雨滴下落的速度 v2 为相对速度,它们之间的 关系为 2 2 1 v = v + v ,于是可得 1 1 2 5.36 m s tg75 − = = v v 题 1.20:设有一架飞机从 A 处向东飞到 B 处,然后又向西飞回到 A 处,飞机相对空气的速 率为 v ,而空气相对地面的速率为 u , A 、B 间的距离为 l ,飞机相对空气的速率 v 保持不 变。(1)假定空气是静止的(即 u = 0 ),试证来回飞机飞行时间为 t = 2l / v 0 ; (2)假定空气的速度向东,试证来回飞行时间为 1 2 2 1 0 (1 ) − = − v u t t ; (3)假定空气的速度向北,试证来回飞行时间为 1/ 2 2 2 2 0 (1 ) − = − v u t t 。 题 1.20 证:由相对速度的矢量关系 v = v + u ,有 (1)空气是静止的,即 u = 0,则往返时,飞机相对地面的 飞行速度 v 就等于相对空气的速度 v ,故飞行往返所需时 间为 v l v l v l t t t = + = + = 2 0 AB BA (2)按题意,当飞机向东时,风速与飞机相对与空气的速度同向;而飞机由东返回时,两者 刚好反向。这时,飞机在往返飞行时,相对于地面的速度值分别为 vAB = v + u 和 vBA = v − u 。 因此,飞行往返所需时间为 1 2 2 1 0 1 − = − − + + = v u t v u l v u l t (3)当空气速度向北时,飞机相对地面的飞行速度的大小由 v = v + u 可得为 2 2 v = v −u ,则飞机往返所需时间为 1/ 2 2 2 2 0 1 2 − = = − v u t v l t 题 1.21:如图所示,一汽车在雨中沿直线行使,其速率为 1 v ,下落雨滴的速度方向偏于竖 直方向之前角 ,速率为 2 v ,若车后有一长方形物体,问车速 1 v 为多大时,此物体正好不会