
(里度本2*大穷 第5章热力学基础 大号物理A教素 第二篇热学 第5章 热力学基础
第5章 热力学基础 大学物理A教案 第二篇 热 学 第5章 热力学基础

国桑水2黄大皇 第5章热力学基础 大学物理A教素 热力学(1) 主要内容: ⊙准静态过程功热量和内能 ⊙热力学第一定律在各等值过程中的应用
第5章 热力学基础 大学物理A教案 热力学(1) 主要内容: 准静态过程 功 热量和内能 热力学第 定律在各等值过程中的应用 热力学第一定律在各等值过程中的应用

国廉本2求大堂 第5章热力学基础 大雪物理A教素 第5章热力学基础 主要内容:热力学第一和第二定律 第一定律是包括热现象在内的能量转换与守恒定律,第二 定律则讨论热功转换的条件和热力学过程进行的方向性。 研究方法: 热力学的研究方法一能量法(宏观法) 以实验事实为基础,从能量观点出发,分析研究物态变化 过程中有关功热转换的关系和条件,是宏观理论
第5章 热力学基础 大学物理A教案 第5章 热力学基础 主要内容: 热力学第一和第二定律 第 定律是包括热现象在内的能量转换与守恒定律 第 第一定律是包括热现象在内的能量转换与守恒定律 定律是包括热现象在内的能量转换与守恒定律,第二 定律则讨论热功转换的条件和热力学过程进行的方向性。 研究方法: 热力学的研究方法 能量法(宏观法) 以实验事实为基础 以实验事实为基础, 从能量观点出发 从能量观点出发, 分析研究物态变化 过程中有关功热转换的关系和条件,是宏观理论

(但度本2黄大穷 第5章热力学基础 大号物理A教素 §5.1准静态过程功热量和内能 1、准静态过程与相图 O准静态过程(approximate static process)(平衡过程): 实际热力学过程的近似,要求过程进行得足够缓慢,过程 中系统的每一个中间状态都是平衡态。 本课程有关计算功和热量的过程均设为准静态过程。 非静态过程一中间状态不是平衡态 ⊙相图:以状态参量为坐标轴构成相空间 平衡态一对应相空间中的一个点 准静态过程一 对应相空间中的一 P。 条线(直线或曲线) 注:热力学中有关计算功和热量的过 程均设为准静态过程
第5章 热力学基础 大学物理A教案 §5 1. 准静态过程 功 热量和内能 1、准静态过程与相图 ◎准静态过程(approximate static process) (平衡过程): 实际热力学过程的近似,要求过程进行得足够缓慢,过程 中系统的每 个中间状态都是平衡态 中系统的每一个中间状态都是平衡态。 本课程有关计算功和热量的过程均设为准静态过程。 非静态过程 中间状态不是平衡态 ◎相图:以状态参量为坐标轴构成 相空间 p 平衡态 —— 对应相空间中的一个点 准静态过程 —— 对应相空间中的一 po 条线(直线或曲线) 注: 热力学中有关计算功和热量的过 V1 V2 V 注 热力学中有关计算功和热量的过 程均设为准静态过程

国廉上黄大避 第5章 热力学基础 大学物理A教素 2、准静态过程中功的计算 功(work)—改变系统状态(改变内能)的一种方式 有规则运动与无规则运动(热运动)之间的能量转换, 与宏观位移相联系。 气缸中气体压强为p时,作 用于活塞的压力为 f=ps 气体作准静态膨胀dl时,气 体对外作的元功为 dw psdl pdv 系统从状态1沿任意过程曲线 到状态2,对外作的总功为 L
第5章 热力学基础 大学物理 A教案 2 准静态过程中功的计算 有规则运动与无规则运动 (热运动 )之间的能量转换, 功(work) ——改变系统状态 (改变内能 )的一种方式 2 、准静态过程中功的计算 有规则运动与无规则运动 (热运动 )之间的能量转换, 与宏观位移相联系。 气 中气体压强为 缸中气体压强为 p 时 作, 用于活塞的压力为 f p s S p f p 气体作准静态膨胀 dl 时,气 体对外作的元功 为 dW psdl pdV d l 系统从状态1沿任意过程曲线 到状态 对外作的总功为 p 1 V2 W dV 到状态2,对外作的总功为 2 V1 W pdV V V1 V2
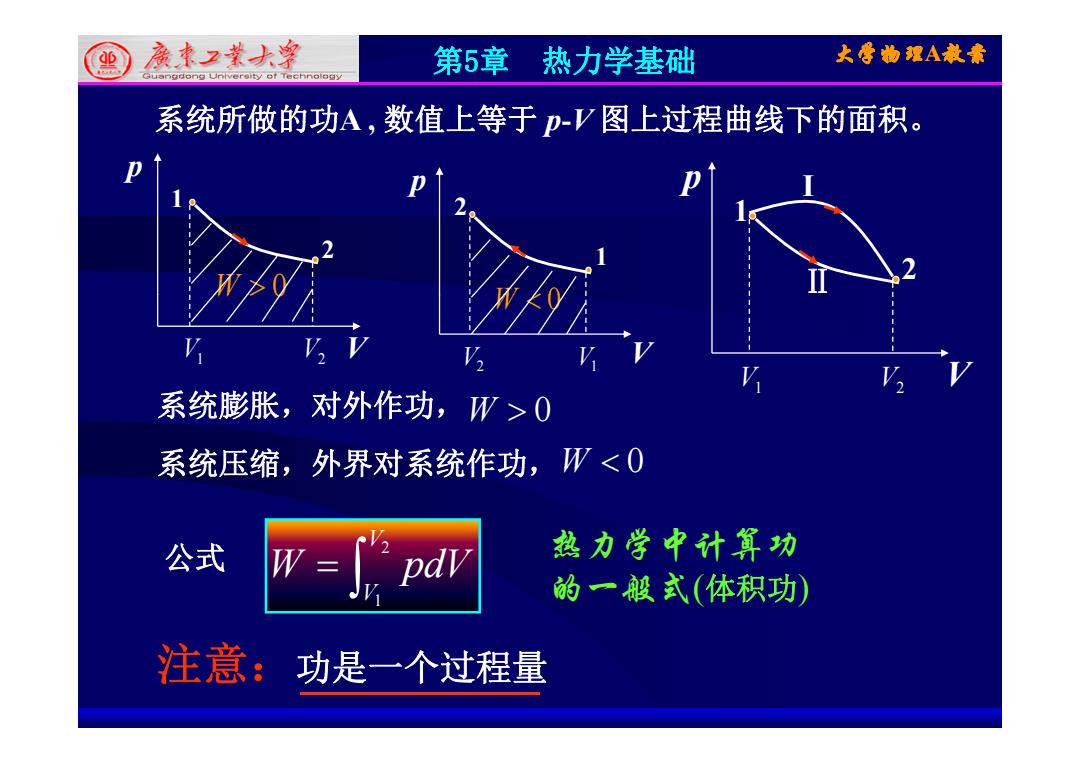
里廉本2求大净 第5章热力学基础 大雪物理A教素 系统所做的功A,数值上等于p-V图上过程曲线下的面积。 系统膨胀,对外作功,W>0 系统压缩,外界对系统作功,W<0 公式 热力学中计算功 的一般式(体积功) 注意:功是 一个过程量
第5章 热力学基础 大学物理A教案 系统所做的功A , 数值上等于 p-V 图上过程曲线下的面积 图上过程曲线下的面积。 p 1 p 2 p 1 I 2 W 0 2 1 W 0 1 Ⅱ 2 V1 V2 V W 0 V2 V1 V W 0 V V V 系统膨胀,对外作功,W 0 系统压缩,外界对系统作功,W 0 V1 V2 V 系统压缩,外界对系统作功,W 0 V2 热力学中计算功 W dV 公式 热力学中计算功 的一般式(体积功) V1 W pdV 公式 注意:功是一个过程量

(但度本2*大皇 第5章热力学基础 大号物理A教素 3、热量ea)—改变系统状态(系统内能)的另一种方式 系统与外界之间热运动能量的传递,通过分子碰撞来实 现,与温差相联系。 热量用Q表示,单位为J。Q>0,表示系统吸热, Q<0,系统放热。 注意:热量Q也是过程量 ◎摩尔热容量Molar specific heat): 1mol物质温度升高1K所吸收的热量。用C表示 C=lim △Qdg A70△TdT J/(mol.K) 因为热量Q是过程量,因此同一物质可有无数个摩 尔热容量。常用的有两个
第5章 热力学基础 大学物理A教案 3、热量(heat) ——改变系统状态(系统内能)的另一种方式 系统与外界之间热运动能量的传递,通过分子碰撞来实 现 与温差相联系 3、热量(heat) ——改变系统状态(系统内能)的另 种方式 现,与温差相联系。 热量用 Q 表示,单位为 J 。Q > 0,表示系统吸热, Q < 0 , 系统放热。 注意:热量Q也是过程量 1 mol 物质温度升高1 K 所吸收的热量。用 C 表示 ◎摩尔热容量(Molar specific heat) : 1 mol 物质温度升高1 K 所吸收的热量。用 C 表示 Q dQ C lim J/(mol K) T dT C T0 lim J/(mol.K) 因为热量 Q 是过程量,因此同 是过程量,因此同 物质可有无数个摩 一物质可有无数个摩 尔热容量。常用的有两个

国桑本2黄大逢 第5章 热力学基础 大雪物理A表素 ⊙定压摩尔热容量C。 1mol气体在等压过程中,温度升高1K所吸收的热量。 C,= do ⊙定容摩尔热容量C 1mol气体在等体过程中,温度升高1K所吸收的热量。 d№ 热力学中计算热量的一般式 C,dT =v"C,di x表示任 意过程
第5章 热力学基础 大学物理A教案 ◎定压摩尔热容量 C dQ 1 mol 气体在等压过程中,温度升高 1 K 所吸收的热量。 ◎定压摩尔热容量 Cp p p dT dQ C 1 mol 气体在等体过程中,温度升高 1 K 所吸收的热量。 ◎定容摩尔热容量 CV V T Q C dd 1 mol 气体在等体过程中,温度升高 1 K 所吸收的热量。 V V dT 热力学中计算 的 般式 热量 一 C dT C dT m Q T T 2 2 x 表示任 C dT C dT 意过程 M Q T x T x x 1 1 意过程

国底之大避 第5章热力学基础 大雪物理A教章 4、 内能(internal energy)— 系统内部的能量 一个反映热力学系统状态特性的宏观物理量。分子动理论观 点:系统的内能是系统内所有分子无规则热运动的动能和分子间 相互作用的势能之总和。气体的内能应是温度和体积的函数。 对理想气体,分子间相互作用力忽略不计,因而无分子势 能,理想气体的内能只是温度的单值函数。 理想气体 内能是个状态量, 内能公式 M2 是温度的单值函数 式中i是分子自由度,单原子气体i=3,双原子气体i=5 多原子气体i=6 热力学中关心的是内能的改变量。一定量的理想气体,温度 由I变到T,时,内能的改变量按下式计算 R(2-T) AE=E2-E=M2
第5章 热力学基础 大学物理A教案 4、内能(internal energy)——系统内部的能量 一个反映热力学系统状态特性的宏观物理量。分子动理论观 点:系统的内能是系统内所有分子无规则热运动的动能和分子间 4、内能(internal energy) 系统内部的能量 点:系统的内能是系统内所有分子无规则热运动的动能和分子间 相互作用的势能之总和。气体的内能应是温度和体积的函数。 对理想气体,分子间相互作用力忽略不计,因而无分子势 RT m i E 内能是个状态量, 能,理想气体的内能只是温度的单值函数。 理想气体 RT M E 2 内能是个状态量, 是温度的单值函数 理想气体 内能公式 式中 是分子自由度 单原子气体 i 3 双原子气体 i 5 热力学中关心的是内能的改变量 一定量的理想气体 温度 式中i是分子自由度,单原子气体 ,双原子气体 多原子气体 i 3 i 5 i 6 热力学中关心的是内能的改变量。 定量的理想气体,温度 由T1变到T2时,内能的改变量按下式计算 m i ( ) 2 1 2 1 2 R T T i Mm E E E

国亲本工黄大皇 第5章热力学基础 大号物撑A教素 §5.2热力学第一定律及其应用 1、热力学第一定律 数学形式: Q=△E+W=E2-E,+ (积分形式) 对于微小过程, do dE pav (微分形式)】 注意: *系统吸热Q>0,系统放热Q0,外界对系统作功W0,系统内能减少△E<0。 *第一类永动机是不可能实现的
第5章 热力学基础 大学物理A教案 §5 2 热力学第一定律及其应用 1、热力学第一定律 §5.2 热力学第 定律及其应用 数学形式: V2 Q E W E E dV (积分形式) 对于微小过程 1 2 1 V Q EW E E pdV (积分形式) 对于微小过程, dQ dE pdV (微分形式) 注意: dQ dE pdV (微分形式) * 系统吸热 Q > 0 ,系统放热 Q 0 ,外界对系统作功 外界对系统作功 W < 0 。 * 系统内能增加 ,系统内能减少 。 E 0 E 0 * 第一类永动机是不可能实现的