
13.7波函数及其统计诠释薛定谔方程 13.7波函数及其统计诠释薛定谔方程 一.物质波波函数及其统计诠释 机械波y(x,t)=yoc0s2π(vt- -i2π(v-) y(x,t)=yoe 实数部分 E 物质波v= 2 -2(E-) Y(x,t)=平oe'h 物质波的波函数 前页后页目录1
前页 后页 目录 1 13.7 波函数及其统计诠释 薛定谔方程 机械波 0 ( , ) cos2π( ) x y x t y t = − 2 0 π( ) ( , ) e x i t y x t y − − = 物质波 , E h h p = = 2 0 π ( ) ( , ) e i Et px Ψ h x t Ψ − − = 物质波的波函数 一. 物质波波函数及其统计诠释 实数部分 13.7 波函数及其统计诠释 薛定谔方程

13.7波函数及其统计诠释薛定谔方程 物质波的物理意义 光波的强度 物质波的强度 光矢量振 波函数振 波动观,点 幅的平方 幅的平方 微粒观点 光子在该处出 粒子在该处出 现的概率大小 现的概率大小 物质波也称概率波 前页后页目录 2
前页 后页 目录 2 13.7 波函数及其统计诠释 薛定谔方程 物质波的物理意义 光波的强度 物质波的强度 波动观点 微粒观点 光矢量振 幅的平方 光子在该处出 现的概率大小 波函数振 幅的平方 粒子在该处出 现的概率大小 物质波也称概率波

13.7波函数及其统计诠释薛定谔方程 平(,t)=Ψoe (B-) 某一时刻某一地点粒子出现的概率正比于 +i2(E-DX) |Ψ2=WΨ* Ψ*=平oe"h dV内,粒子出现的概率正比于 I平2dΨ=哑*dV |平卫称为概率密度 空间粒子出现的总概率等于1,所以 ∬ΨPdV=1称为归一化条件 波函数是单值、连续、有限而且归一化的。 前页后页目录 3
前页 后页 目录 3 13.7 波函数及其统计诠释 薛定谔方程 某一时刻某一地点粒子出现的概率正比于 2 | | Ψ dV内,粒子出现的概率正比于 2 | | d Ψ V 2 | | Ψ 称为概率密度 空间粒子出现的总概率等于1,所以 2 | | d Ψ V =1 称为归一化条件 波函数是单值、连续、有限而且归一化的。 ΨΨ = ΨΨ dV = 2 0 π ( ) ( , ) e i Et px Ψ h x t Ψ − − = 2 0 π ( ) * e i Et px Ψ Ψ h + − =
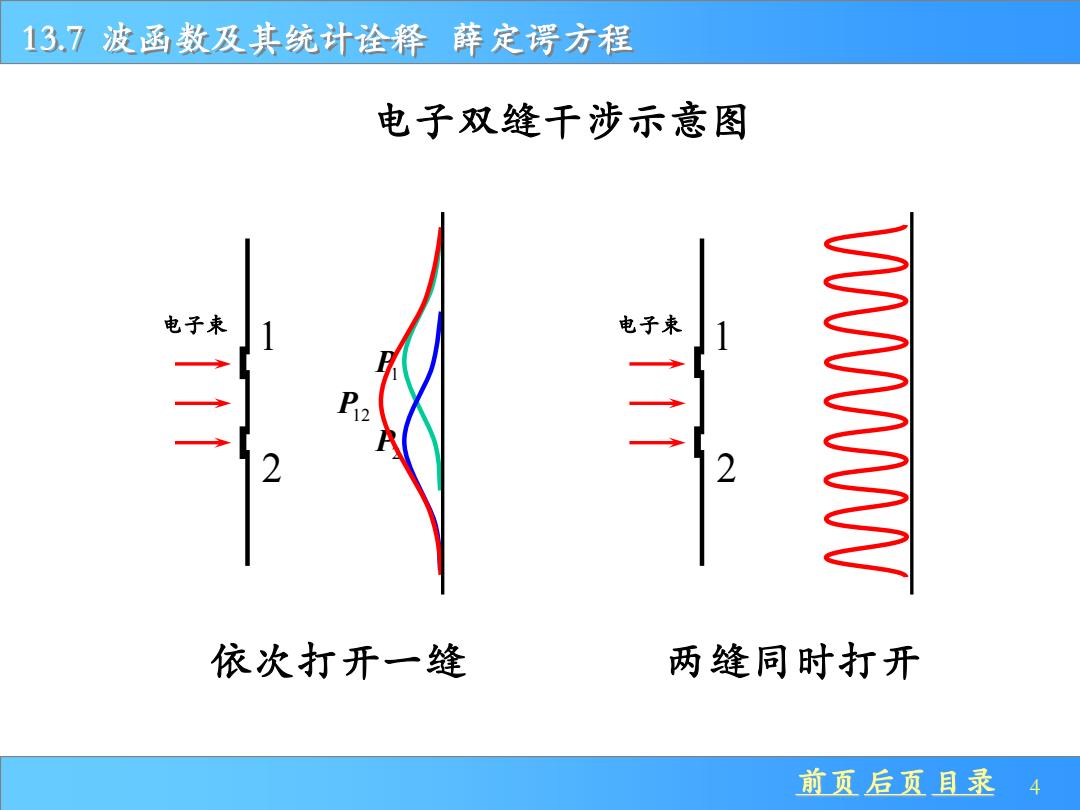
137波函数及其统计诠释薛定谔方程 电子双缝干涉示意图 电子束 W 依次打开一缝 两缝同时打开 前页后页目录 .4
前页 后页 目录 4 13.7 波函数及其统计诠释 薛定谔方程 2 1 电子束 电子双缝干涉示意图 2 1 电子束 P12 依次打开一缝 P1 P2 两缝同时打开

13.7波函数及其统计诠释薛定谔方程 电子双缝干涉图 100 3000 70000 前页后页目录 5
前页 后页 目录 5 13.7 波函数及其统计诠释 薛定谔方程 电子双缝干涉图 7 100 3000 70000

137波函数及其统计诠释薛定谔方程 二.薛定谔方程 1.自由粒子的薛定谔方程 波函数Ψ(x,t)=平eh四 =oe i(Et-px) 求偏导数 a2Ψ p2 2 方 ot h 并利用E=mo2=p2 2 2m (非相对论) 前页后页目录 6
前页 后页 目录 6 13.7 波函数及其统计诠释 薛定谔方程 1. 自由粒子的薛定谔方程 波函数 2 0 π ( ) ( , ) e i Et px Ψ h x t Ψ − − = 1 0 ( ) e i Et px Ψ − − = 求偏导数 2 2 2 2 Ψ p Ψ x = − Ψ i EΨ t = − 并利用 2 1 2 2 2 p E m m = = v (非相对论) 二. 薛定谔方程

137波函数及其统计诠释薛定谔方程 一维运动自由粒子含时的薛定谔方程 2a2Ψ 2m dx2 8t 2.在势场中粒子的薛定谔方程 E=P-+U(x,t) 2m 波函数对t的偏导数 oΨ_iD+Ux,t0Ψ Ot h2m 前页后页目录 7
前页 后页 目录 7 13.7 波函数及其统计诠释 薛定谔方程 一维运动自由粒子含时的薛定谔方程 2 2 2 2 Ψ Ψ i m t x − = 2. 在势场中粒子的薛定谔方程 2 2 ( , ) p E U x t m = + 波函数对t 的偏导数 2 2 [ ( , )] Ψ i p U x t Ψ t m = − +

13.7波函数及其统计诠释薛定谔方程 势场中一维运动粒子含时的薛定谔方程 262Ψ 2m dx2 +U(化)Ψ=i访0平 Ot 势场中三维运动粒子含时的薛定谔方程 2(a2Ψ,a2Ψ,a2Ψ 2max2 +U(x,3,)Ψ=0吧 拉普拉斯算符V三 2 02 前页后页目录 8
前页 后页 目录 8 13.7 波函数及其统计诠释 薛定谔方程 势场中一维运动粒子含时的薛定谔方程 2 2 2 2 ( , ) Ψ Ψ U x t Ψ i m t x − + = 势场中三维运动粒子含时的薛定谔方程 2 2 2 2 2 2 2 2 ( , , , ) Ψ Ψ Ψ Ψ U x y z t Ψ i m t x y z − + + + = 拉普拉斯算符 2 2 2 2 2 2 2 x y z + +

13.7波函数及其统计诠释薛定谔方程 薛定谔方程 g+U0K,z,0y=h 2m ot 再根据初始条件和边界条件,求解薛定谔方程, 就可得到的波函数。 3.定态薛定谔方程 势函数与时间无关时 Ψ(x,y,,t)=Ψ(x,y,z)f(t) 将上式代入薛定谔方程,分离变量 前页后页目录 9
前页 后页 目录 9 13.7 波函数及其统计诠释 薛定谔方程 薛定谔方程 2 2 2 ( , , , ) Ψ Ψ U x y z t Ψ i m t − + = 再根据初始条件和边界条件,求解薛定谔方程, 就可得到的波函数。 势函数与时间无关时 Ψ( , , , ) ( , , ) ( ) x y z t = ψ x y z f t 将上式代入薛定谔方程,分离变量 3. 定态薛定谔方程

137波函数及其统计诠释薛定谔方程 yK,y)+Uxy,3w(x, 1 =ihf1 2m Ψ(x,y,) at f(t) 必然两边等于同一常数(E),则 是y(化,z)+Ux,2w(c =E 2m Ψ(x,y,z) h01 =E at f(t) 前页后页目录10
前页 后页 目录 10 13.7 波函数及其统计诠释 薛定谔方程 2 2 1 1 2 ( ) ( , , ) ( , , ) ( , , ) ( , , ) ( ) f t x y z U x y z x y z i m x y z t f t − + = 必然两边等于同一常数(E),则 2 2 1 2 ( , , ) ( , , ) ( , , ) ( , , ) x y z U x y z x y z E m x y z − + = ( ) 1 ( ) f t i E t f t =