广东工业大学：《大学物理》课程教学资源（课件讲稿）第一篇 力学 第1章 质点运动学（自然坐标系中的速度和加速度、不同坐标系中速度和加速度的变换关系）

(但亲本2黄大穷 第1章质点运动学 大骨物理A煮兼 质点运动学（2) 主要内容： 。自然坐标系中的速度和加速度 。不同坐标系中速度和加速度的变换关系

第1章 质点运动学 大学物理A教案 质点运动学(2) 主要内容： 自然坐标系中的速度和加速度 不同坐标系中速度和加速度的变换关系

国桑水2黄大等 第1章质点运动学 大骨物理A款素 §1-3自然坐标系中的速度和加速度 1.自然坐标系(natural coordinate system 以轨迹上任一点o作为坐标 的原点，轨迹曲线为坐标轴建立 的坐标系称为自然坐标系。 △S 坐标轴的方向分别取切线 和法线两正交方向。 规定：切向坐标轴沿质点前进方向的切向为正，单位矢量为云 法向坐标轴沿轨迹的法向凹侧为正，单位矢量为刀 注意：在自然坐标系中，单位矢量的方向随时间变化 2.速度和速率 速度： ds 速率： ds dt dt

第1章 质点运动学 大学物理A教案 §1-3 自然坐标系中的速度和加速度 以轨迹上任 一点o作为坐标   P n  §1 3 自然坐标系中的速度和加速度 1.自然坐标系(natural coordinate system) 以轨迹上任 点o作为坐标 的原点, 轨迹曲线为坐标轴建立 的坐标系称为自然坐标系。  s n s n  o  坐标轴的方向分别取切线 Q  和法线两正交方向。 切向坐标轴沿质点前进方向的切向为正，单位矢量为  法向坐标轴沿轨迹的法向凹侧为正 单位矢量为 规定：  法向坐标轴沿轨迹的法向凹侧为正，单位矢量为 n 注意: 在自然坐标系中, 单位矢量的方向随时间变化. ２.速度和速率 速度： ds 速率 ds    dt ds v  速率： dt ds v 

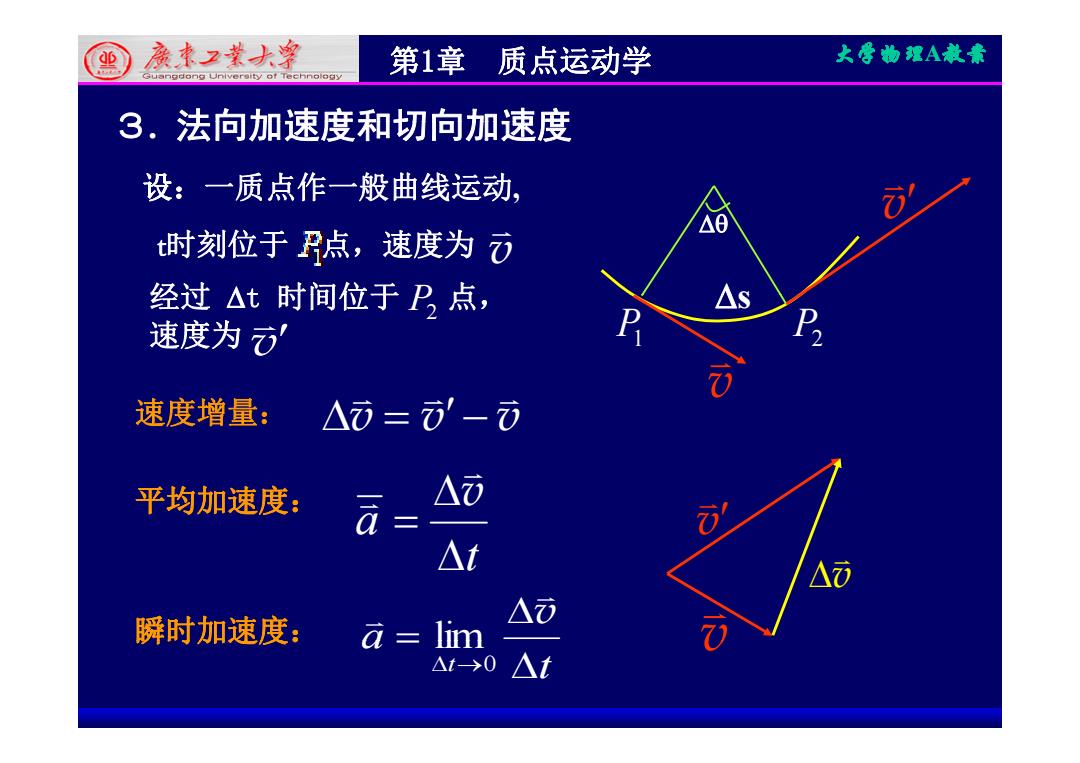
廉本2求大等 第1章质点运动学 大学物理A教兼 3.法向加速度和切向加速度 设：一质点作一般曲线运动， t时刻位于点，速度为 经过△t时间位于P点， 速度为 速度增量： △市=-0 平均加速度： △0 a= △t 瞬时加速度： △ò a=lim A→0△t

第1章 质点运动学 大学物理A教案 ３. 法向加速度和切向加速度 设：一质点作一般曲线运动, v  t时刻位于 点，速度为 v 经过 t 时间位于 P 点 v  经过 t 时间位于 点， s 速度为 P2 v  P1 P2 v  s 速度增量： v v v       v 平均加速度： t a    v   v  t 瞬时加速度： a   v  lim v v   瞬时加速度： t a t    0 lim v

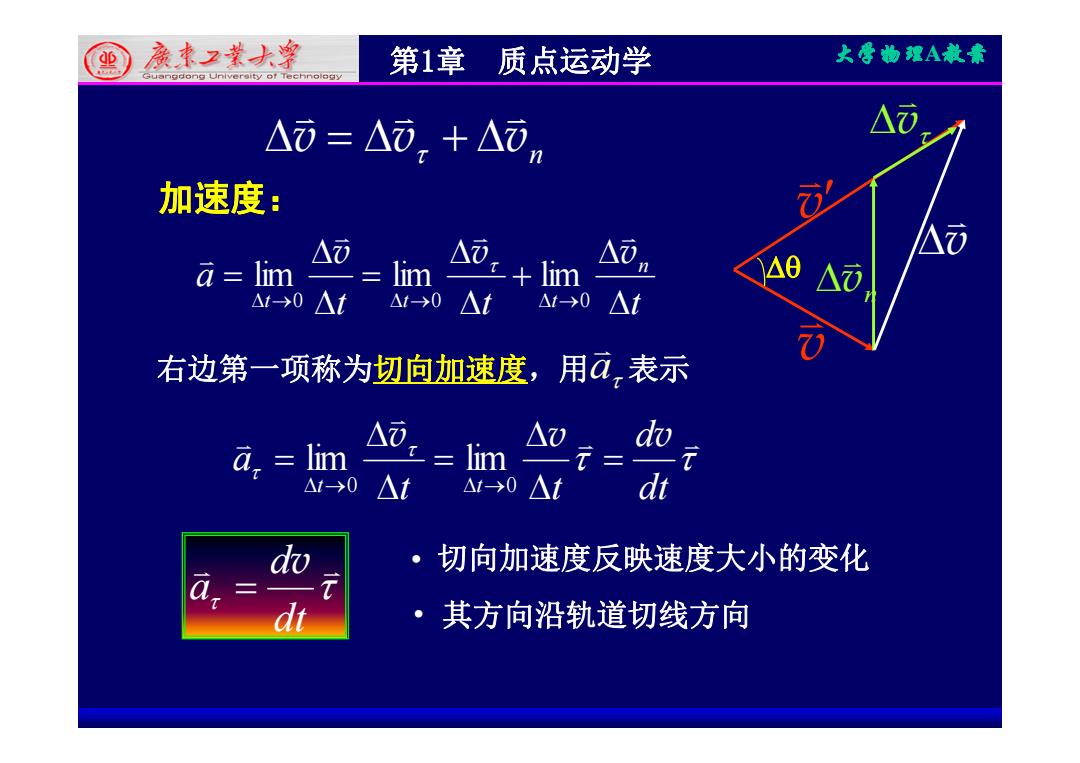
(里度本2*大皇 第1章质点运动学 大骨物理A煮兼 △⑦=△，十△i △ 加速度： △可 △i, △ a=lim=lim lim △0 △ 1→0△t△1-→0△t△1→0△t 右边第一项称为切向加速度，用ā，表示 a,lim A,=lim A=do △1→0t△1→0△t dt dv ·切向加速度反映速度大小的变化 ·其方向沿轨道切线方向

第1章 质点运动学 大学物理A教案 v         v  v n v v v          加速度： v  vn   t t t a n          v v v     0 0 0 lim lim  lim 加速度： v   v  n t t t t0  t0  t0  右边第一项称为切向加速度，用a表示         d a v v v      lim lim 右边第 项称为切向加速度 用 表示    t t dt a t0  t0  lim lim dv • 切向加速度反映速度大小的变化 • 其方向沿轨道切线方向     dt d a v 

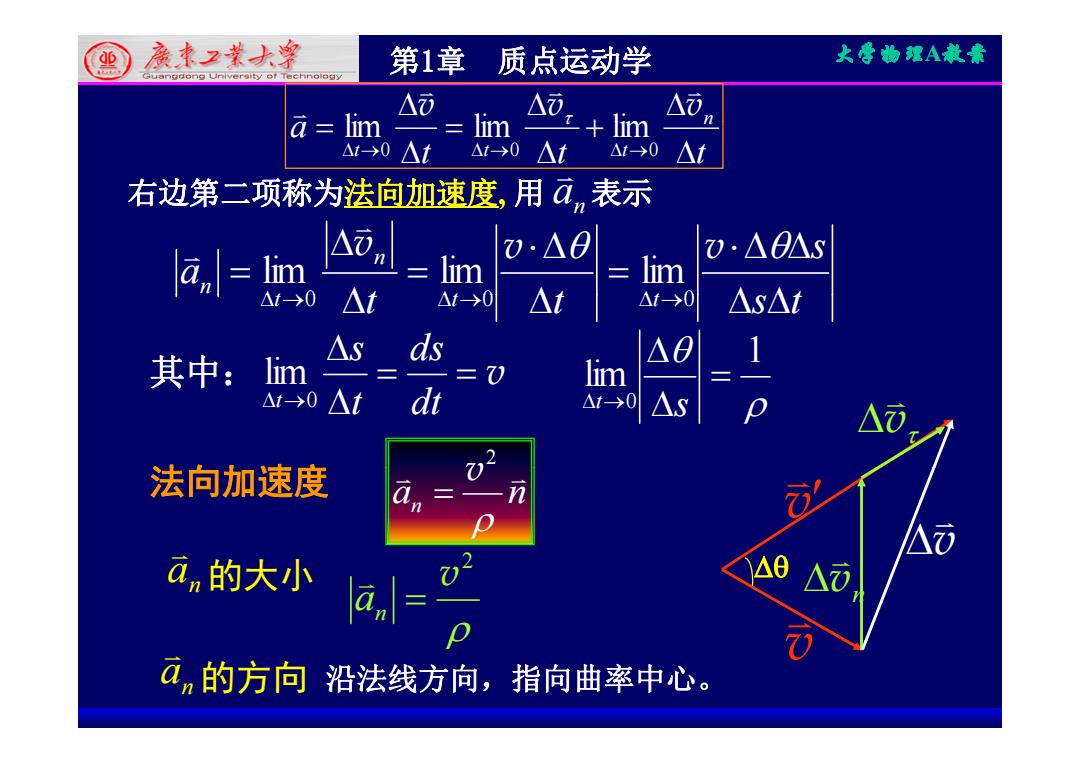
()亲东2*大学 第1章质点运动学 大零物理A款素 △ A.+lm △ =四A+ 右边第二项称为法向加速度，用ā，表示 △ v:△0 a,lim =lim 0△0△s lim 「A0△t-→0 △t △1-→0 △s△t 其中：lim △sds △0 1 =V lim △→0△t dt 10△S △) 法向加速度 3 -n 72 an的大小 la.= △6△ 0 ān的方向沿法线方向，指向曲率中心

第1章 质点运动学 大学物理 A教案  n   v  v v     lim lim  lim 右边第二项称为法向加速度, 用 表示 a n 表示  t t t a n t t t         0   0   0 lim lim  lim , n t s t t a t t n t n                  v v  v  0 0 0 lim lim lim   其中：   v  s ds lim  1 lim   t t s t  t  0   t  0   t  0   其中： v    t dt t 0 lim  lim  0  s t 法向加速度 2 v v   法向加速度 2 a n n    v  v   v    2 v a n   v   v n   v a n 的大小   沿法线方向，指向曲率中心。 v a n 的方向 

盟廉本黄大曾 第1章质点运动学 大学物理A教兼 全加速度： a=a,+a 全加速度的大小： a-vatal 全加速度的方向： 0=arctan 4 a 例6物体作斜抛运动，测得A点的速度为)，方向如图所 示.则A点的a,和曲率半径p各为多少？ 解：由图有 a,=-gsin30°=- a,-8cos30°-3 8 0s 213v an 3 g

第1章 质点运动学 大学物理A教案 全加速度： a a a    全加速度：   全加速度的大小： 2 2  a a a  n   a a a  n  全加速度的方向：  a an  arctan a 例6 物体作斜抛运动,测得A点的速度为 , 方向如图所 示 则A点的 a 和曲率半径 各为多少? v  示. 则A点的 和曲率半径 各为多少? a  解: 由图有 300 g a  g sin   v 解 由图有 2 a  g sin30   a g g 3 cos300    0 A 30 a  a  a g g n 2   cos30  2 2 v 2 3 v g  an  a g n 3 v 2 3 v    

国亲本2黄大净 第1章质点运动学 大骨物理A煮兼 3.圆周运动(circle motion) 圆周运动是一般曲线运动的一个特例，曲率半径恒为R。 ()圆周运动的角量描述 1)角位置0角位移△0 角位置(angular position)0: R 质点所在的位矢下与x轴正 向的夹角，单位是弧度rad。 角位移(angular displacement)△0： 质点从A到B位矢F转过的角度， 单位是弧度rad 规定：逆时针转向△0为正， 顺时针转向△0为负 2)角速度0 △eda (angular speed) 0= (rad.s △tdt

第1章 质点运动学 大学物理A教案 3. 圆周运动( ) circle motion) 圆周运动是一般曲线运动的一个特例，曲率半径恒为R。 (1) 圆周运动的角量描述 B s R B 1) 角位置 角位移 角位置(angular position)  A  R  角位置(angular position)  ： 质点所在的位矢 与x轴正 向的夹角 单位是弧度 rad。 r  o x 向的夹角,单位是弧度 rad。 角位移(angular displacement) : 质点从A到B位矢 r转过的角度  规定 逆时针转向为正 顺时针转向为负 质点从A到B位矢 转过的角度, 单位是弧度 rad. r 规定：逆时针转向为正, 顺时针转向为负 ( d )1 li  d 2) 角速度 (rad s )1 0 lim         dt d t t   (angular speed) 

国桑水2美大皇 第1章 质点运动学 大骨物理A款素 3)角加速度c心 a=lim △odw (rad.s-2 (angular acceleration) △1>0 △tdt (2)线量linear measures)与角量(angular measures)的关系 ds s=RO 0= R9 Ro dt dt dv a.= -=Ra =Ro c dt an= (3)匀速圆周运动： 70 0=恒量，a=0,a,=0, a=a, -=02R (④)一般变速圆周运动： dv c≠0， a= dt R

第1章 质点运动学 大学物理A教案 ( d )2 li 3)角加速度   d (rad s )2 0 lim         dt d t t    (2) 线量(li )与角量(l )的关系 ) (angular acceleration) (2) 线量(linear measures)与角量(angular measures)的关系 s  R   R d R ds s  R v    R dt R dt v     R d R dv 2 2 v (3) 匀速圆周运动    R dt R dt a    2 R R an   v (3) 匀速圆周运动： R R a an 2 2    v   恒量，  0， a  0， (4) 一般变速圆周运动： R  n dv 2 v ， dt d a v   R an v   0， 

国廉本黄大皇 第1章质点运动学 大学物理A教素 变速圆周运动的总加速度 a=a,+a, 总加速度的大小 a= va +a 用角量表示匀加速圆周运动的基本公式： 0=0+Ct 1 0=80t@1+2at o2=o0+2a(0-0）

第1章 质点运动学 大学物理A教案 变速圆周运动的总加速度  a a a n     n   总加速度的大小 2 2 a  a  a 用角量表示匀加速圆周运动的基本公式  a a a  n  用角量表示匀加速圆周运动的基本公式：    t 2 0 0 0 1             t t t   0 20 2 0 0 2 2              t  t   0 0

(国亲本2黄大净 第1章质点运动学 大骨物理A煮兼 例7半径为r=0.2m的飞轮，可绕0轴转动。已知轮缘 上一点M的运动方程为p=-t+4t,求在1秒时刻M点的 速度和加速度。 解： 0=d0=-21+4 do Q= =-2 dt dt 0=r0=r(-2t+4)=0.2×(-2×1+4)=0.4m·s1 a,=r0=0.2×(-2)=-0.4ms2 an=r02=0.2(-2×1+4)2=0.8ms2 M a=√a+a7=0.89ms2 0 A tan =tan-10.8 =63.4° a, 0.4

第1章 质点运动学 大学物理A教案 例7 半径为r = 0 2. m的飞轮 可绕 ， o 轴转动 已知轮缘 轴转动。已知轮缘 上一点M的运动方程为 =-t2 + 4t ，求在1秒时刻M点的 速度和加速度。 解：   2t  4 dt d    2 dt d  dt 1 ( 2 4) 0.2 ( 2 1 4) 0.4 m s v  r  r  t         2 0 2 ( 2) 0 4 2    0.2(2)  0.4 ms  a r 2 2 2 0.2( 2 1 4) 0.8 m s a  r       n v  n ( ) M 2 2 2 0.89 m s     n a a a  n a   a   M  n       63 4 1 1 0.8  tan tan an a o x    63 4 0 4 . . tan tan   a