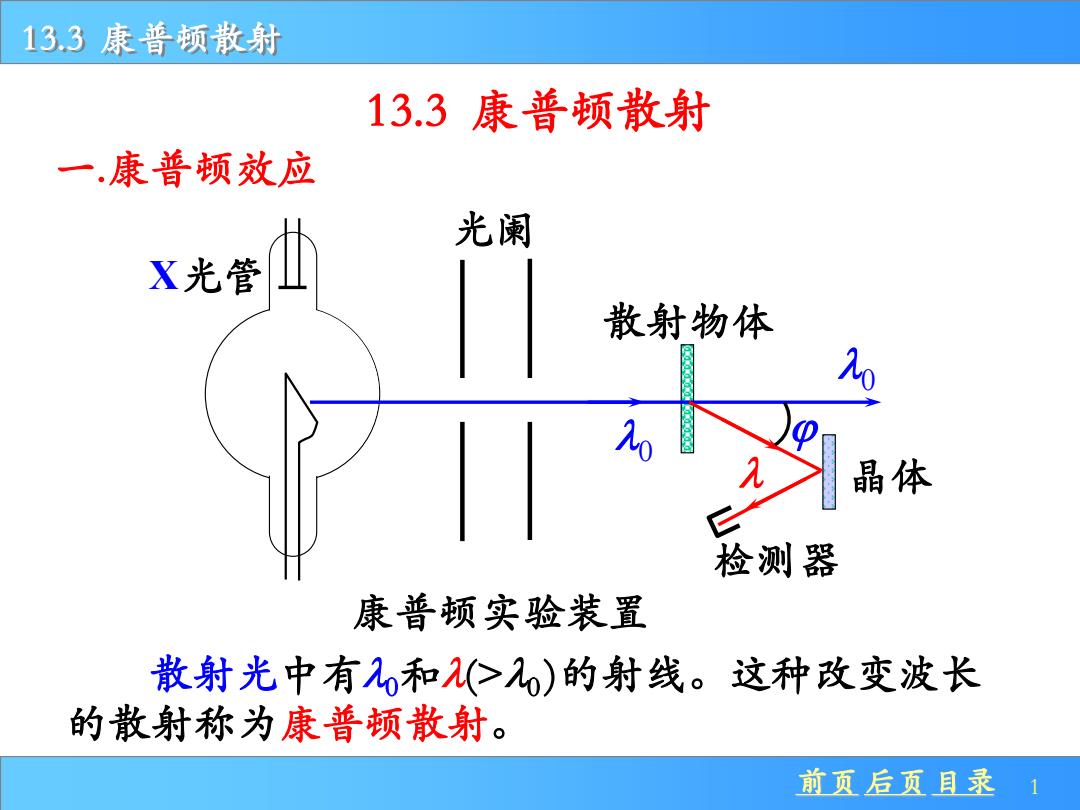
13.3康普顿散射 13.3康普顿散射 一.康普顿效应 X无誉的 光阑 散射物体 晶体 检测器 康普顿实验装置 散射光中有几和(仁几0)的射线。这种改变波长 的散射称为康普顿散射。 前页后页目录 1
前页 后页 目录 1 13.3 康普顿散射 一.康普顿效应 散射光中有0和(>0 )的射线。这种改变波长 的散射称为康普顿散射。 X光管 光阑 散射物体 晶体 检测器 康普顿实验装置 0 0 13.3 康普顿散射
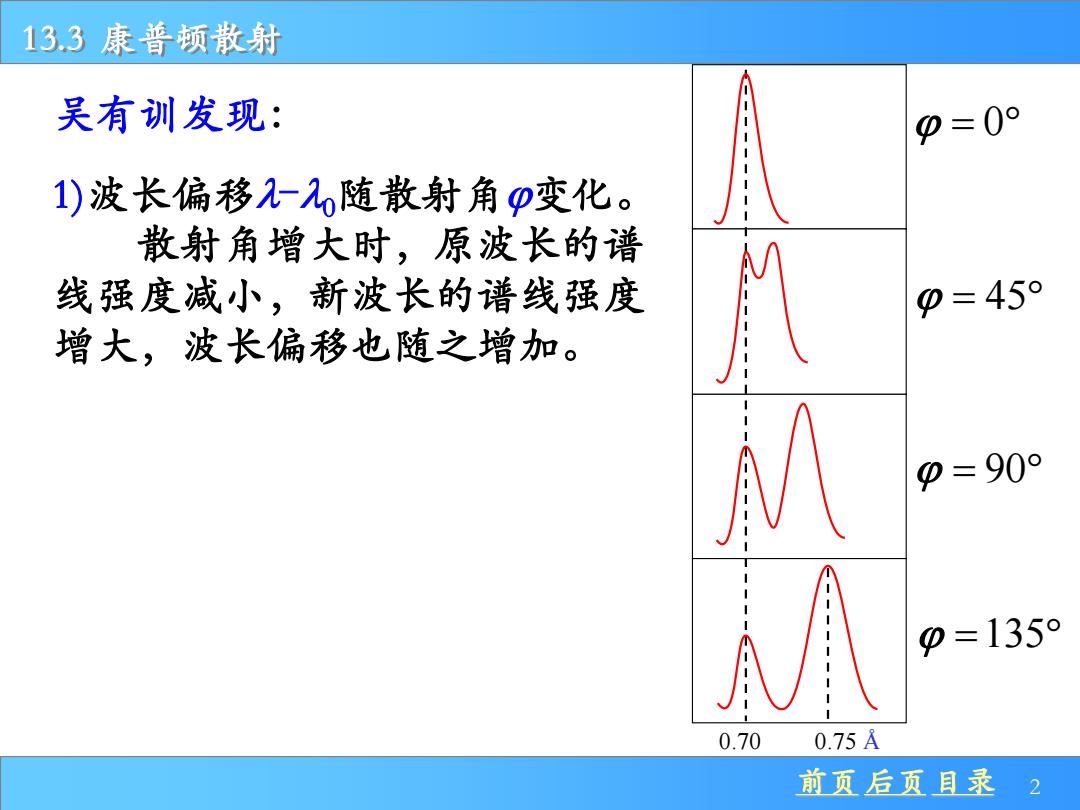
13.3康普顿散射 吴有训发现: p=0° 1)波长偏移2-2,随散射角p变化。 散射角增大时,原波长的谱 线强度减小,新波长的谱线强度 p=45° 增大,波长偏移也随之增加。 p=90° p=135° 0.700.75A 前页后页目录 2
前页 后页 目录 2 13.3 康普顿散射 吴有训发现: 1)波长偏移-0随散射角变化。 散射角增大时,原波长的谱 线强度减小,新波长的谱线强度 增大,波长偏移也随之增加。 = 0 = 45 = 90 = 135 0.70 0.75 Å
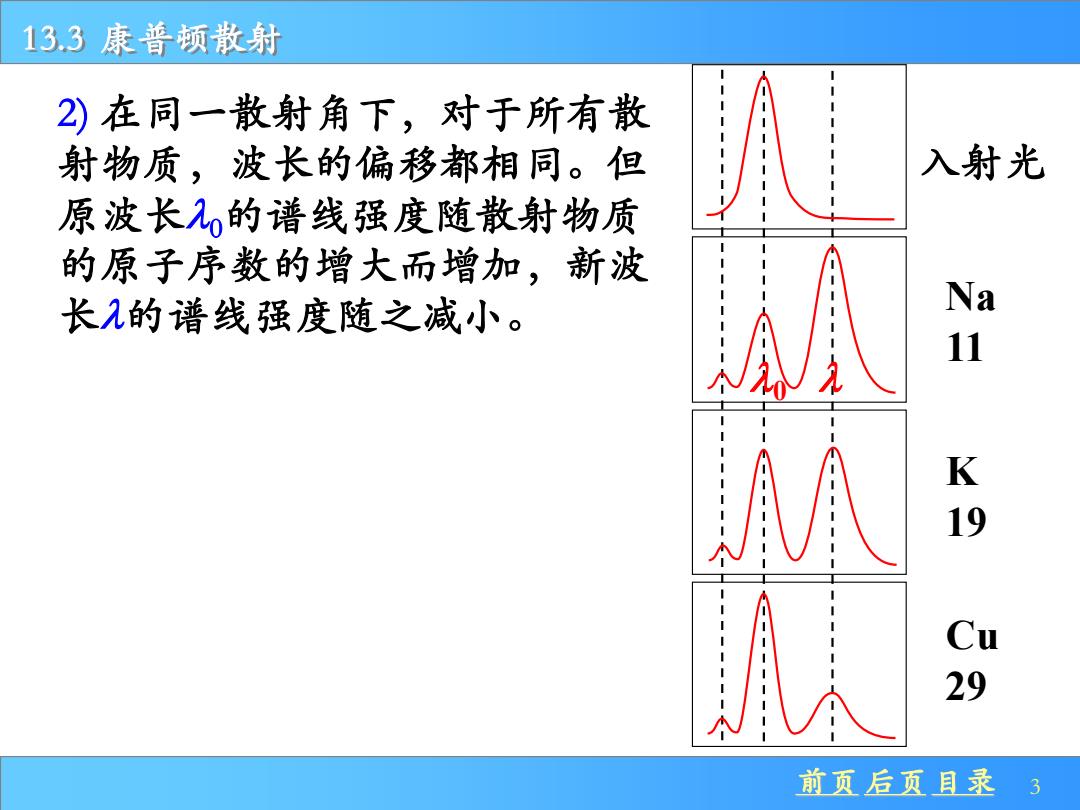
13.3康普顿散射 2)在同一散射角下,对于所有散 射物质,波长的偏移都相同。但 入射光 原波长入的谱线强度随散射物质 的原子序数的增大而增加,新波 长入的谱线强度随之减小。 Na 11 K 19 A Cu 29 前页后页目录 3
前页 后页 目录 3 13.3 康普顿散射 2) 在同一散射角下,对于所有散 射物质,波长的偏移都相同。但 原波长0的谱线强度随散射物质 的原子序数的增大而增加,新波 长的谱线强度随之减小。 入射光 Na 11 K 19 Cu 29 0

13.3康普顿散射 康普顿散射无法用光的波动理论解释 二.光子理论的解释 1)光子与原子(或束缚很紧的内层电子)相碰撞 散射光的波长等于入射光的波长。 2)光子与自由电子(或束缚微弱的外层电子)相碰撞 散射光的波长大于入射光的波长。 前页后页目录 4
前页 后页 目录 4 13.3 康普顿散射 康普顿散射无法用光的波动理论解释 2)光子与自由电子(或束缚微弱的外层电子)相碰撞 散射光的波长大于入射光的波长。 1)光子与原子(或束缚很紧的内层电子)相碰撞 散射光的波长等于入射光的波长。 二. 光子理论的解释

13.3康普顿散射 康普顿散射的理论计算 由能量守恒和动量守恒 lv +mc2=lvo+moc2 hvo mo coso+mucos= c m)' -sino-musin=0 mo m= 解得△1=1-不)=2hsi 22=24sin2 -sin moc 2 h 电子的康普顿波长2。= =2.43×10-12(m) moc 前页后页目录 5
前页 后页 目录 5 13.3 康普顿散射 康普顿散射的理论计算 由能量守恒和动量守恒 2 2 h mc h m c 0 0 + = + 0 cos cos h h m c c + = v sin sin 0 h m c − = v 解得 0 2 2 1 m m c = − v x y m0 h 0 h v m = − 0 2 0 2 2 sin h m c = 电子的康普顿波长 0 c h m c = 12 2 43 10 . (m) − = 2 2 2 c sin =

13.3康普顿散射 例1 波长为0.02nm的X射线与静止的自由电子碰 撞,从与入射方向成0°度角的方向观察散射射线。 求:(1)散射X射线的波长;(②)反冲电子获得的能量; (3)反冲电子的动量。P230例题13-5 解:(1)散射后波长改变 △= 2h n29 sin mc 2 Av =2.4×10-12(m) m =0.0024(nm) 前页后页目录 6
前页 后页 目录 6 13.3 康普顿散射 x y m0 h 0 例1 波长为0.02nm的X射线与静止的自由电子碰 撞,从与入射方向成90º度角的方向观察散射射线。 求:(1)散射X射线的波长;(2)反冲电子获得的能量; (3)反冲电子的动量。P230例题13-5 解:(1) 散射后波长改变 2 0 2 2 sin h m c = 12 2 4 10 0 0024 . (m) . (nm) − = = h v m

13.3康普顿散射 散射后,X射线的波长 =△2+=0.0024+0.02=0.0224(nm) (②)由能量守恒得,反冲电子获得的能量(动能) △E。=,-hm=hc_hc_hcA 元22o 6.63×10-34×3×108×2.4×10-12 2×1011×2.24×10-1m =10.7×10-16(J)=6.66×103(eV) 前页后页目录 7
前页 后页 目录 7 13.3 康普顿散射 (2) 由能量守恒得,反冲电子获得的能量(动能) E h h e 0 = − 34 8 12 11 11 6 63 10 3 10 2 4 10 2 10 2 24 10 . . . − − − − = 16 3 10 7 10 6 66 10 . (J) . (eV) − = = 散射后,X射线的波长 = + = 0 0024 0 02 0 0224 . . . (nm) = + 0 0 hc hc = − 0 hc =
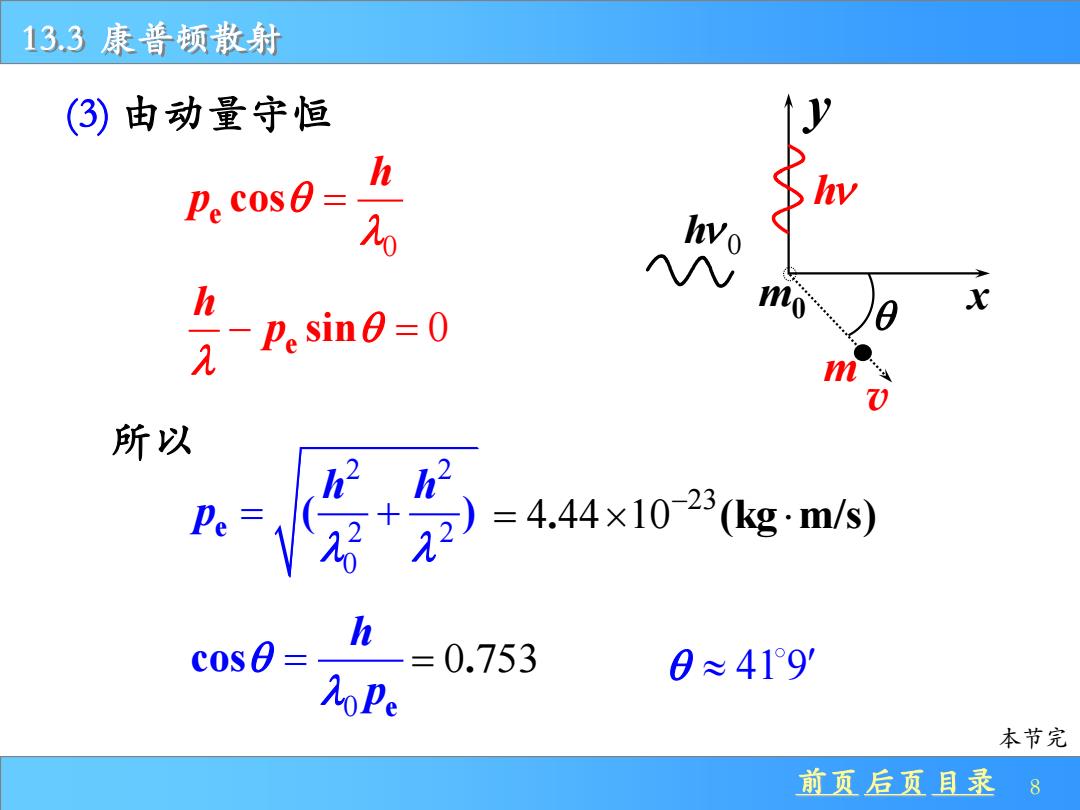
13,3康普顿散射 (3)由动量守恒 ↑Jy Pe cose=h p.sino=0 h m 所以 2 2)=4.44×1028(kg·m/s) h cos0= -=0.753 0≈41°9 AoPe 本节完 前页后页且录 8
前页 后页 目录 8 13.3 康普顿散射 (3) 由动量守恒 0 e cos h p = 0 e sin h p − = 所以 2 2 2 2 0 e ( ) h h p = + 23 4 44 10 . (kg m/s) − = 0 e cos h p = = 0 753 . 41 9 本节完 x y m0 h 0 h v m