
11.8波的叠加原理波的干涉驻波 11.8波的叠加原理波的千涉驻波 一.波的叠加原理 波传播的独立性 波的叠加原理 几列波同时在介质 中传播时,它们的传播 特性(波长、频率、波 速、波形)不会因其它 波的存在而受到影响。 在相遇的区域,合振动 是分振动的叠加。 前页后页目录 1
前页 后页 目录 1 11.8 波的叠加原理 波的干涉 驻波 一.波的叠加原理 波传播的独立性 波的叠加原理 几列波同时在介质 中传播时,它们的传播 特性(波长、频率、波 速、波形)不会因其它 波的存在而受到影响。 在相遇的区域,合振动 是分振动的叠加。 11.8 波的叠加原理 波的干涉 驻波
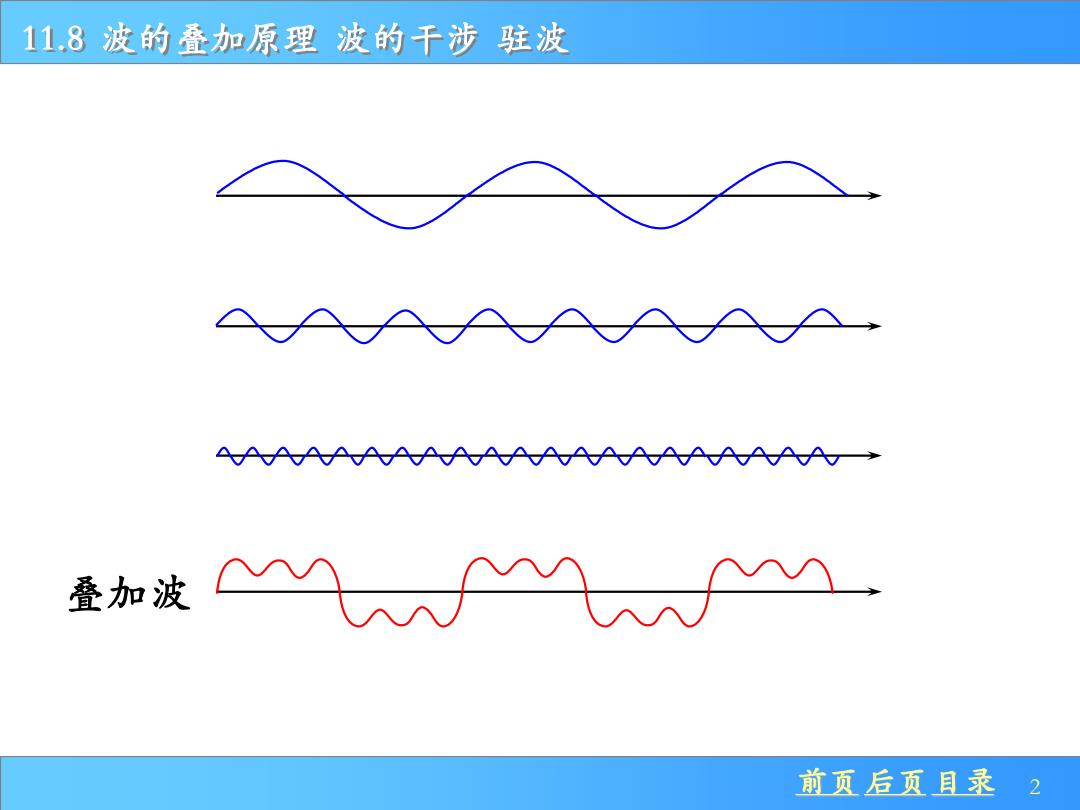
11.8波的叠加原理波的干涉驻波 AAAAA 叠加波 nJM√M 前页后页目录2
前页 后页 目录 2 11.8 波的叠加原理 波的干涉 驻波 叠加波
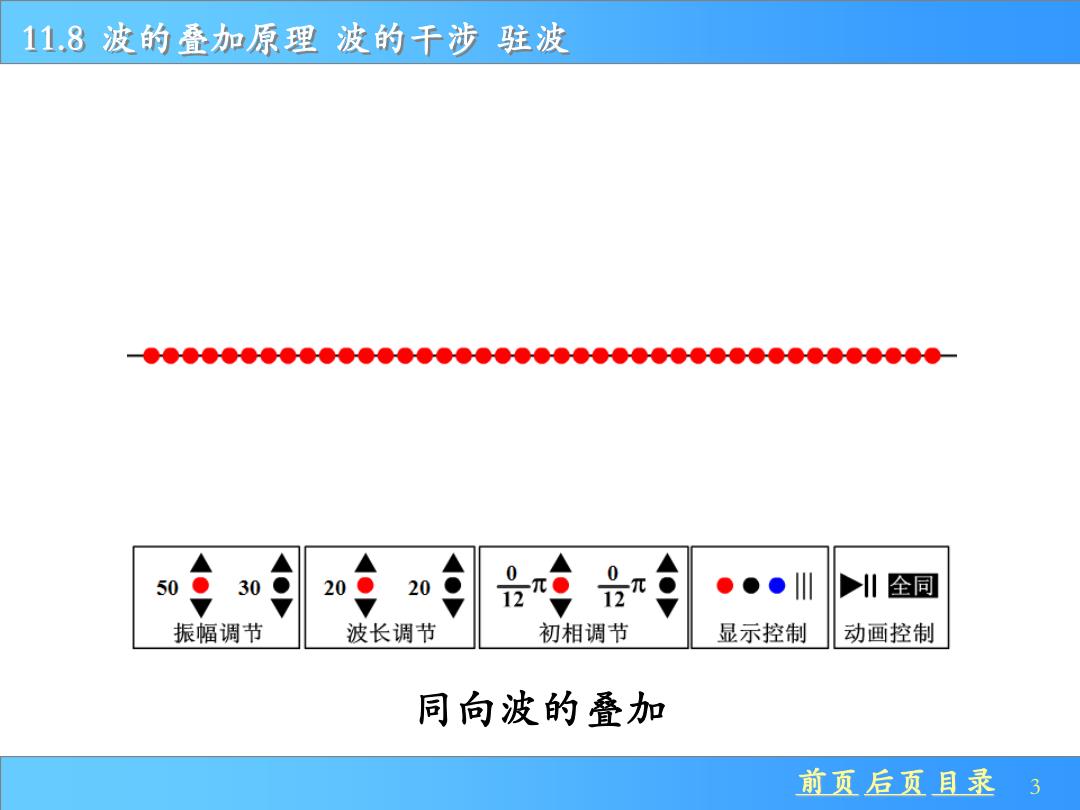
11.8波的叠加原理波的干涉驻波 ●●●●●●0●●●●●●●●●●●0●●●●●●0●●●0●00●●0●0●00 30 20 20 。●●l ‖全同 振幅调节 波长调节 初相调节 显示控制 动画控制 同向波的叠加 前页后页目录 3
前页 后页 目录 3 11.8 波的叠加原理 波的干涉 驻波 同向波的叠加
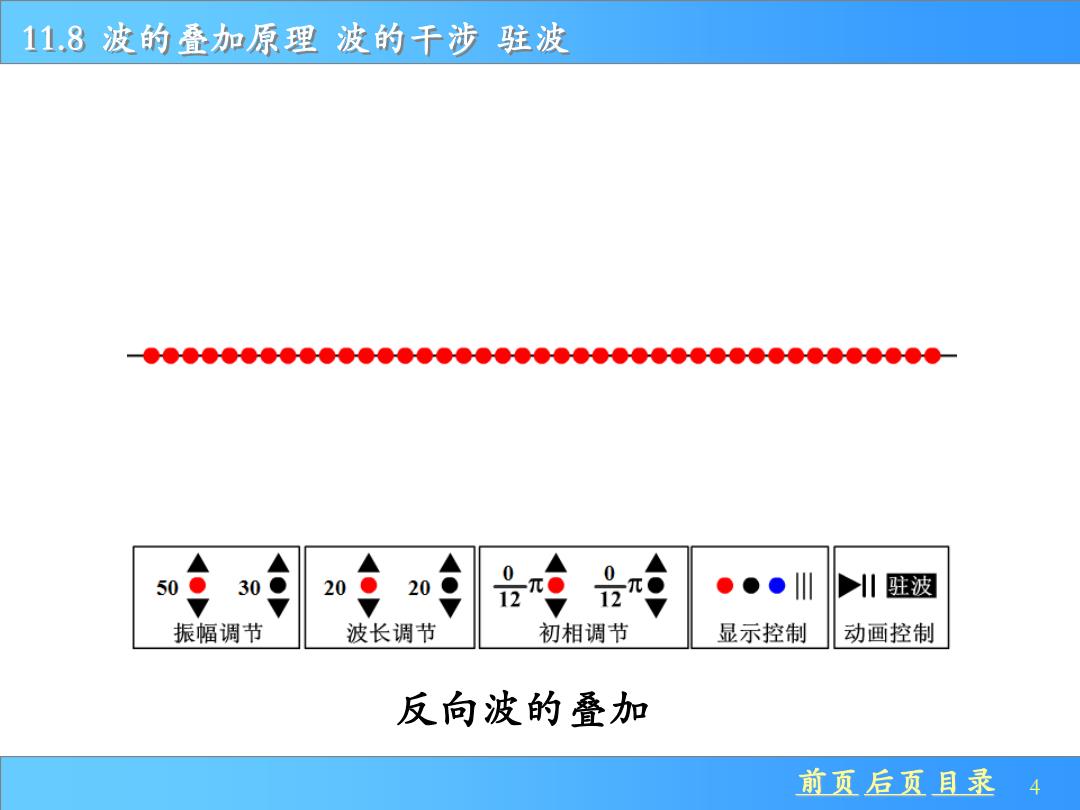
11.8波的叠加原理波的干涉驻波 ●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●● 50● 30● 20 20● 0元● 127 ●●●川 川驻波 振幅调节 波长调节 初相调节 显示控制 动画控制 反向波的叠加 前页后页且录4
前页 后页 目录 4 11.8 波的叠加原理 波的干涉 驻波 反向波的叠加

11.8波的叠加原理波的干涉驻波 二.波的千涉 满足相干条件的两列波 在空间相遇时,某些点的振 动始终加强,而另一些点的 振动始终减弱的现象。 相干条件: 振动方向相同、频率相 同、相位差恒定。 相干波:满足相干条件的波 相干波源:能激发相干波的波源 前页后页目录5
前页 后页 目录 5 11.8 波的叠加原理 波的干涉 驻波 二.波的干涉 相干条件: 满足相干条件的两列波 在空间相遇时,某些点的振 动始终加强,而另一些点的 振动始终减弱的现象。 相干波: 相干波源: 振动方向相同、频率相 同、相位差恒定。 满足相干条件的波 能激发相干波的波源
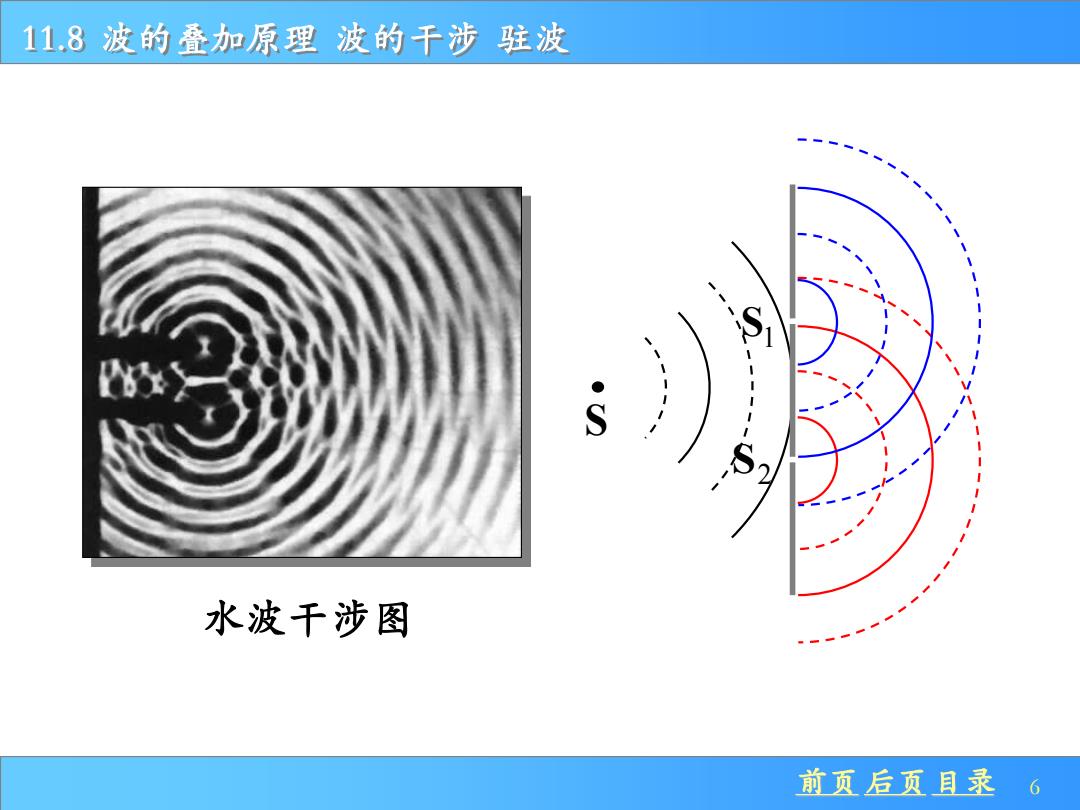
11.8波的叠加原理波的干涉驻波 水波干涉图 前页后页目录 6
前页 后页 目录 6 11.8 波的叠加原理 波的干涉 驻波 水波干涉图 S 1 S S2

11.8波的叠加原理波的干涉驻波 合振幅分布 S1和S2的振动表式 r=SP y1o Ao cos(@t+do) 2=S2P Jy20=A20c0s(0t+p20)) S 传到P,点的振动表式 1=Ac0s(t+40- 2) y2=42 cos(@t+o 22 前页后页目录 7
前页 后页 目录 7 11.8 波的叠加原理 波的干涉 驻波 合振幅分布 S1 S2 r2 2 = S PP S r1 1 = S P 1和S2的振动表式 传到P点的振动表式 y A t 10 10 10 = + cos( ) y A t 20 20 20 = + cos( ) 1 1 1 10 2 = + − π cos( ) r y A t 2 2 2 20 2 = + − π cos( ) r y A t

11.8波的叠加原理波的干涉驻波 y=A cos(@t+o- 2)y y2=A2c0s(0t+420- 2h) P,点的合振动y=+y2=Ac0s(Dt+4) 其中A=4++2A4,c0(0-40)2 π(2-1) A sin(o- 2π)+A,sin(p2o d arctan 2π Ac0s(40- L)+A2c0s(40 前页后页目录 8
前页 后页 目录 8 11.8 波的叠加原理 波的干涉 驻波 P点的合振动 其中 2 2 2 1 1 2 1 2 20 10 2 2 π( ) cos ( ) r r A A A A A − = + + − − 1 2 1 10 2 20 0 1 2 1 10 2 20 2 2 2 2 π π sin( ) sin( ) arctan π π cos( ) cos( ) r r A A r r A A − + − = − + − 0 y y y = +1 2 = + A t cos( ) 1 1 1 10 2 = + − π cos( ) r y A t 2 2 2 20 2 = + − π cos( ) r y A t
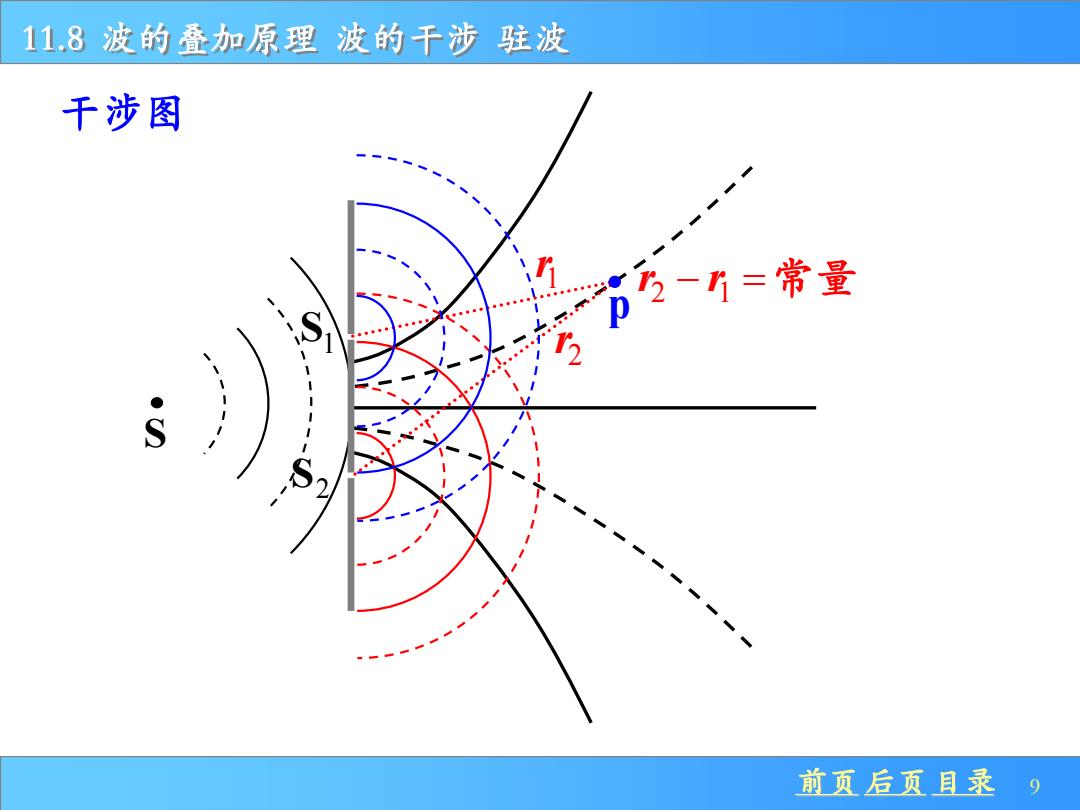
11.8波的叠加原理波的干涉驻波 干涉图 2-=常量 ● 前页后页目录 9
前页 后页 目录 9 11.8 波的叠加原理 波的干涉 驻波 干涉图 1 r 2 r p 2 1 r r − =常量 S S1 S2

11.8波的叠加原理波的干涉驻波 +8+24wr肉--2 (1)△=±2km(k=0,1,2,) A=A+A2(合振幅极大)干涉相长 (2)△p=±(2k-1)π(k=1,2,…) A=A-A2|(合振幅极小,可能为0)干涉相消 (3)其它 A-4kA<A+A2 前页后页目录 10
前页 后页 目录 10 11.8 波的叠加原理 波的干涉 驻波 (1) (合振幅极大)干涉相长 (2) (合振幅极小,可能为0)干涉相消 (3) 其它 2 2 2 1 1 2 1 2 20 10 2 2 π( ) cos ( ) r r A A A A A − = + + − − = = 2 0 1 2 k k π ( , , ,...) = − = ( ) 2 1 1 2 k k π ( , ,...) A A A = +1 2 1 2 A A A = − | | 1 2 1 2 | | A A A A A − +