9.4自感应和自感应 9.4自感应和自感应 一.自感应 自感现象:通电回路电流变化时,在自身回路中激发 感应电动势的现象。这种电动势叫做自感电动势。 A ⑧ B R 前页后页目录 1
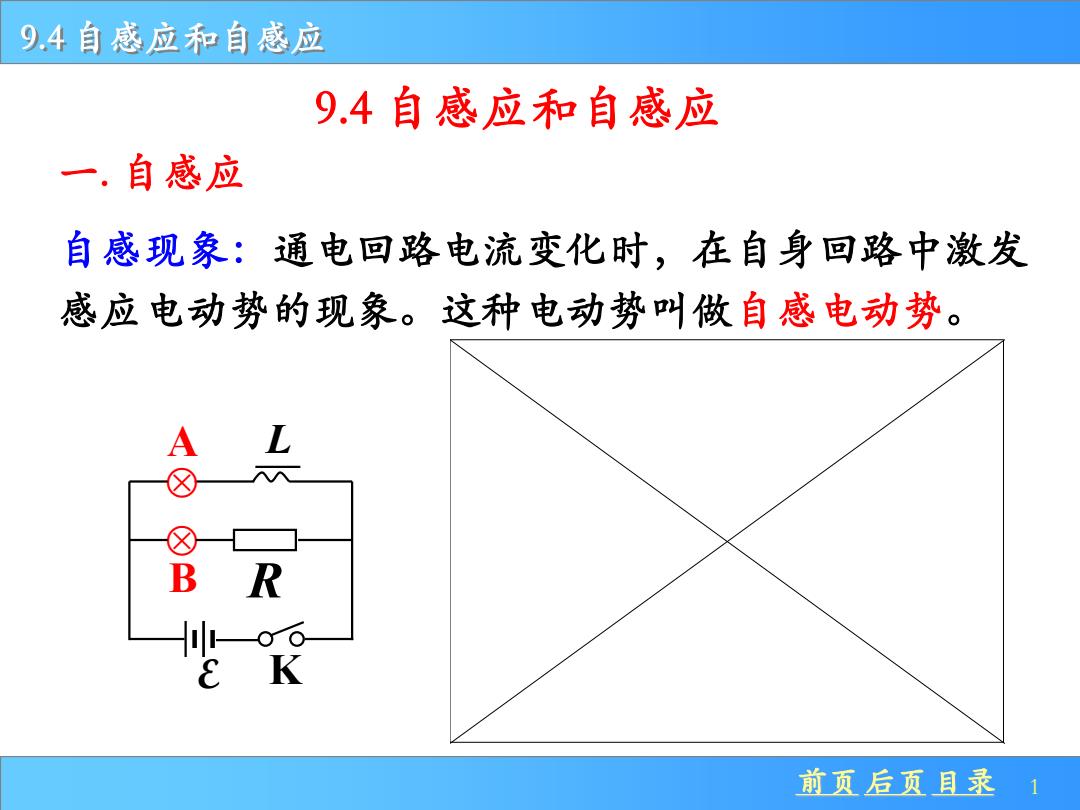
9.4 自感应和自感应 前页 后页 目录 1 自感现象:通电回路电流变化时,在自身回路中激发 感应电动势的现象。这种电动势叫做自感电动势。 A L K B R E 9.4 自感应和自感应 一. 自感应

9.4自感应和自感应 自感电动势 dΦy_dΦxdl_ dtd亚dt -Id/ dt 自感系数(自感、电感) L=dON dI SI制:H(亨利) 1H=103mH=106H 前页后页目录2
9.4 自感应和自感应 前页 后页 目录 2 自感电动势 d d N L Φ t E = − d d d d ΦN I I t = − d d I L t = − 自感系数(自感、电感) d d ΦN L I = SI制:H(亨利) 3 6 1 10 10 H mH = = μH

9.4自感应和自感应 例1设长为的空芯长直螺线管,截面半径为R,均 匀密绕N匝线圈。求螺线管的自感系数。 解:线圈的磁链 ΦN=NBS=N4nlS=hn2IV 自感系数 L=dox=Bon'v 本题完 前页后页目录 3
9.4 自感应和自感应 前页 后页 目录 3 例1 设长为l的空芯长直螺线管,截面半径为R,均 匀密绕N匝线圈。求螺线管的自感系数。 解:线圈的磁链 ΦN = NBS = N nIS 0 2 = 0n IV 自感系数 本题完 d d ΦN L I = 2 = 0n V
9.4自感应和自感应 例2同轴电缆可看作由两根“无限长”同轴圆筒导 体所组成,沿内、外圆筒通有等值反向电流I。求电 缆单位长度上的自感。(设内、外圆筒的半径分别为 R1和R2)P414例题7 R 前页后页目录4
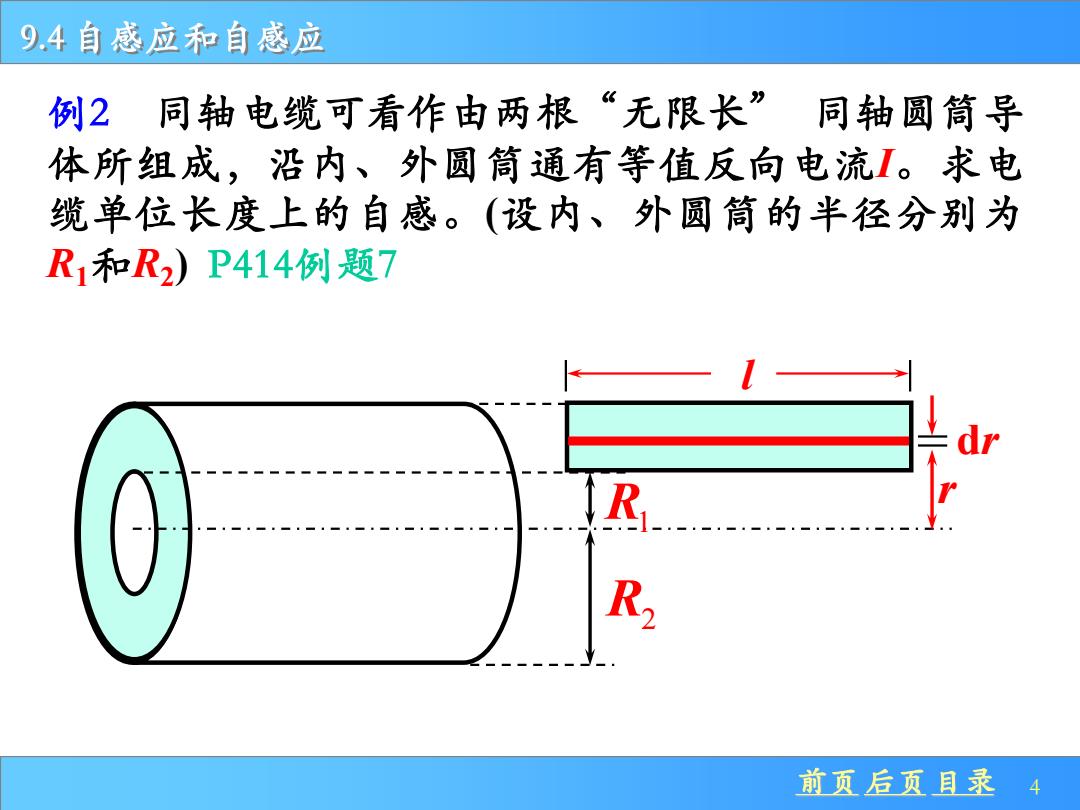
9.4 自感应和自感应 前页 后页 目录 4 例2 同轴电缆可看作由两根“无限长” 同轴圆筒导 体所组成,沿内、外圆筒通有等值反向电流I。求电 缆单位长度上的自感。(设内、外圆筒的半径分别为 R1和R2 ) P414例题7 R1 R2 l r dr

94自感应和自感应 解:由安培环路定理 B=0 (rR2) B=tl (R2>r>R) 2元r dΦ=Bldr= HoLldr 2πr -人b-仙=”是 2πR 前页后页目录 5
9.4 自感应和自感应 前页 后页 目录 5 解:由安培环路定理 1 2 B r R r R = 0 ( ) 0 2 1 2 ( ) π I B R r R r = 0 2 d d d π I Φ Bl r l r r = = S Φ = dΦ 2 0 1 2 d π R R I l r r = 0 2 1 2 ln π Il R R = l r dr

9.4自感应和自感应 单位长度上的自感 dΦ_ln In R2 L==2元"R 如果,其间充满磁导率为山的磁介质,则 Lo= 2πR 本题完 前页后页目录 6
9.4 自感应和自感应 前页 后页 目录 6 单位长度上的自感 0 d d Φ L l I = 0 2 1 2 ln π R R = 如果,其间充满磁导率为μ的磁介质,则 2 0 1 2 ln π R L R = 本题完

9.4自感应和自感应 二.互感应 前页后页目录 7
9.4 自感应和自感应 前页 后页 目录 7 二. 互感应
9.4自感应和自感应 互感现象:一个回路电流变化在另一个回路产生感应 电动势的现象。这种电动势叫做互感电动势。 doL =-M2l d dt 82= dΦ2=-M12dt dt dΦ2L= M12=M21=M称为互感系数, M= dΦ12 d dl 简称互感。 前页后页目录 8
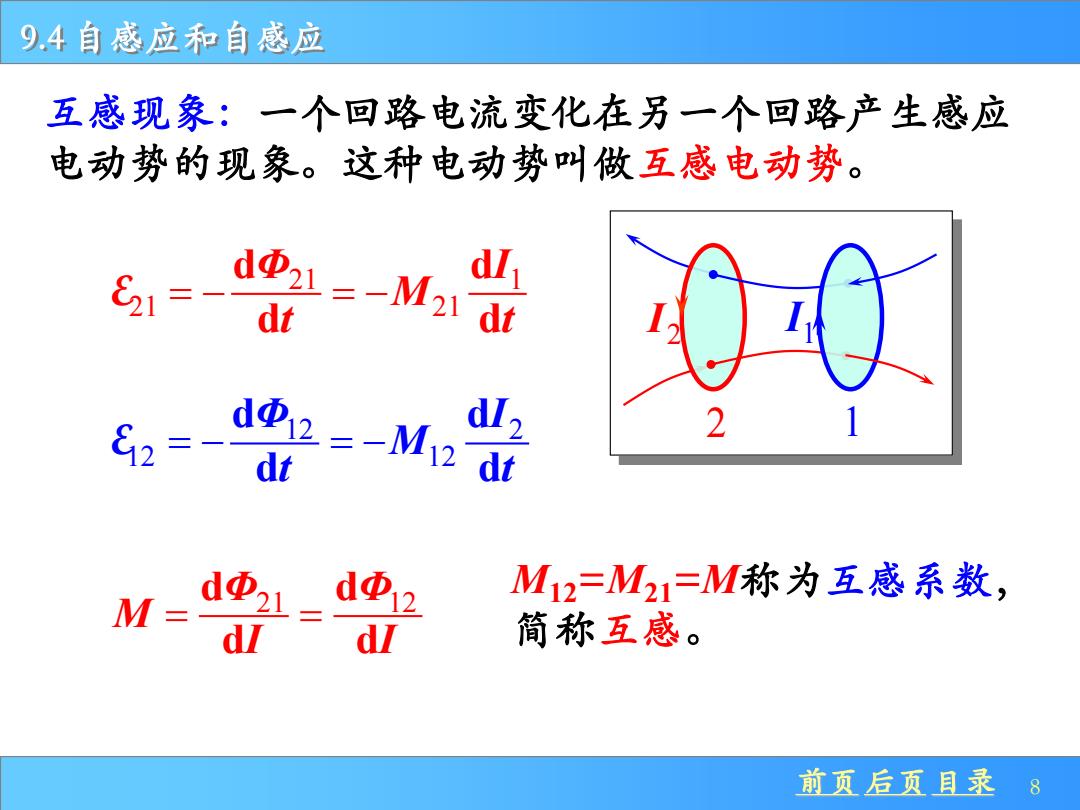
9.4 自感应和自感应 前页 后页 目录 8 互感现象:一个回路电流变化在另一个回路产生感应 电动势的现象。这种电动势叫做互感电动势。 2 I 1 I 2 1 M12=M21=M称为互感系数, 简称互感。 21 1 21 21 d d d d Φ I M t t E = − = − 12 2 12 12 d d d d Φ I M t t E = − = − d d 21 12 d d Φ Φ M I I = =

9.4自感应和自感应 例3无限长直螺线管,单位长度 有n匝线圈。半径为r的小圆环放在 螺线管内,小圆环平面与管轴垂直。 求螺线管与小圆环的互感系数。 解:设螺线管中电流为L1,螺线管内磁场 B=uonI 小圆环的磁通量 中21=Bπr2=4nl1r2 互感系数M=4,元r2 本题完 前页后页目录 9
9.4 自感应和自感应 前页 后页 目录 9 例3 无限长直螺线管,单位长度 有n匝线圈。半径为r的小圆环放在 螺线管内,小圆环平面与管轴垂直。 求螺线管与小圆环的互感系数。 解:设螺线管中电流为I1,螺线管内磁场 B nI 1 0 1 = 小圆环的磁通量 互感系数 2 M n r = 0 π 本题完 2 2 Φ21 1 0 1 = = B r nI r π π

9.4自感应和自感应 耦合因数 M=kLL (0<k≤1) 00 k称为两回路间的耦合因数。 本节完 前页后页目录10
9.4 自感应和自感应 前页 后页 目录 10 耦合因数 1 2 M k L L k = ( ) 0 1 k称为两回路间的耦合因数。 本节完 2 I 1 I 2 1