
⑧4稳恒磁场的高斯定理与安培环路定理 8.4稳恒磁场的高斯定理 与安培环路定理 一.稳恒磁场的高斯定理 通过任意闭合曲面S的总磁通量总等于零。 乐B-ds=0 比较求Eds=4 80 磁场是无源场、涡旋场 fE.a7=o ∮Bdl=? 前页后页目录 1
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 1 一. 稳恒磁场的高斯定理 通过任意闭合曲面S的总磁通量总等于零。 0 S B S = d 比较 0 i S d q E S = 磁场是无源场、涡旋场 8.4 稳恒磁场的高斯定理 与安培环路定理 0 L E l = d L B l = d ?

84稳恒磁场的高斯定理与安培环路定理 二.安培环路定理 1.载流长直导线磁场的环流 1)环路包围电流时 ④B.dM=④Bcos6ul n tol rdop ΓJ02πr =4I © doB 结论:磁感应强度的环流与环 路的形状无关,与闭合环路内 所包围的电减森發方向有关。 前页后页且录2
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 2 ,与积分方向有关。 ,与闭合环路内 所包围的电流有关 I 1. 载流长直导线磁场的环流 1) 环路包围电流时 I 二. 安培环路定理 L dl dB L Bdl L = B l cos d 2 0 π = rd 0 2π I r 0 = I 结论:磁感应强度的环流与环 路的形状无关 r
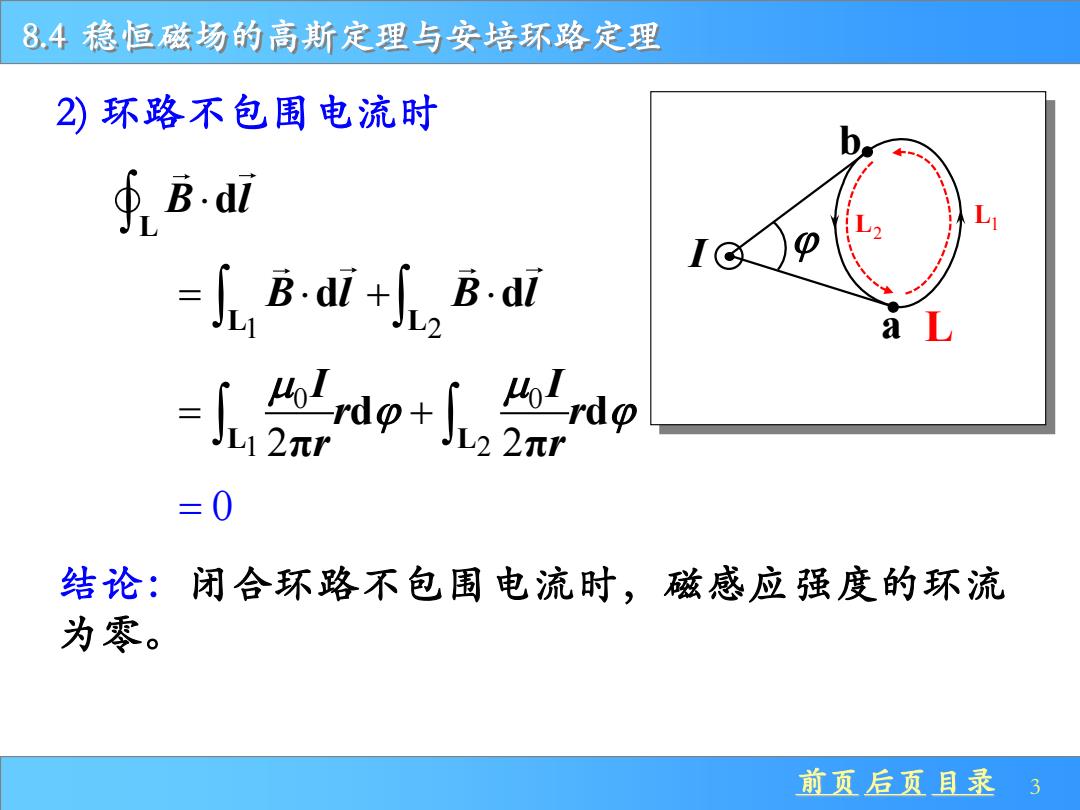
8,4稳恒磁场的高斯定理与安培环路定理 2)环路不包围电流时 ∮Bdl -h BdiB olrdp JL22πr =0 结论:闭合环路不包围电流时,磁感应强度的环流 为零。 前页后页目录3
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 3 2) 环路不包围电流时 L1 = B l d 0 0 L L 1 2 2 2 d d π π I I r r r r = + = 0 结论:闭合环路不包围电流时,磁感应强度的环流 为零。 I a b L L B l d L1 L2 L2 + B l d

84稳恒磁场的高斯定理与安培环路定理 2.安培环路定理 在恒定电流的磁场中,磁感应强度沿任一闭合 路径L的线积分(磁感强度的环流),数值上等于路 径L所包围的电流强度的代数和的4倍。 Bd7=o∑I 取正 符号法则:积分路径的绕行方 向与电流成右手螺旋关系时, 取负 取正;反之取负。 前页后页目录 4
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 4 2. 安培环路定理 在恒定电流的磁场中,磁感应强度沿任一闭合 路径L的线积分(磁感强度的环流),数值上等于路 径L所包围的电流强度的代数和的0倍。 0 L L B l I = d 符号法则:积分路径的绕行方 向与电流成右手螺旋关系时, 取正;反之取负。 I 取负 L I 取正 L
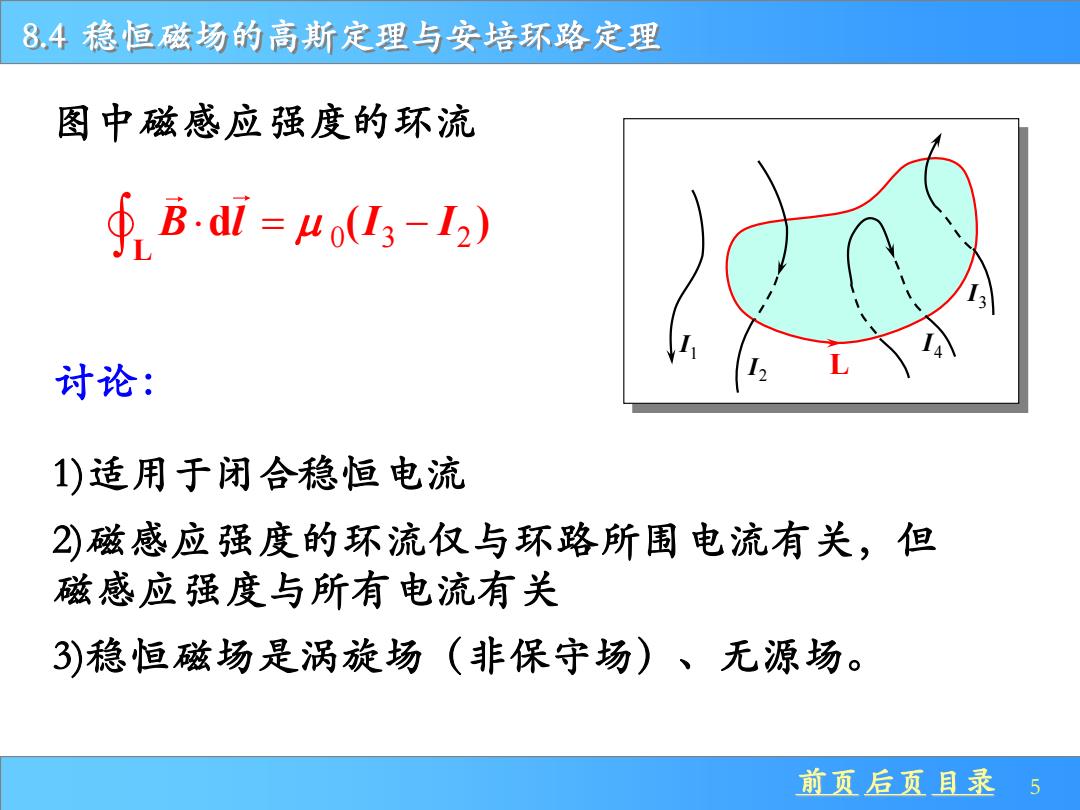
8,4稳恒磁场的高斯定理与安培环路定理 图中磁感应强度的环流 ∮Bdl=4o(4-1) 讨论: 1)适用于闭合稳恒电流 2)磁感应强度的环流仅与环路所围电流有关,但 磁感应强度与所有电流有关 3)稳恒磁场是涡旋场(非保守场)、无源场。 前页后页目录 5
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 5 I2 L 1I 3I 4 I 图中磁感应强度的环流 讨论: 1)适用于闭合稳恒电流 2)磁感应强度的环流仅与环路所围电流有关,但 磁感应强度与所有电流有关 3)稳恒磁场是涡旋场(非保守场)、无源场。 0 3 2 L B l I I = − d ( )

8.4稳恒磁场的高斯定理与安培环路定理 三.安培环路定理的应用 ∮B.dl=u∑I L 计算磁感应强度步骤: 1)分析磁场的对称性,确定磁场的方向; 2)选择合适的闭合积分环路; 3)计算磁感应强度的环流; 4)应用安培环路定理,求B。 前页后页目录 6
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 6 计算磁感应强度步骤: 1)分析磁场的对称性,确定磁场的方向; 2)选择合适的闭合积分环路; 3)计算磁感应强度的环流; 4)应用安培环路定理,求B。 三. 安培环路定理的应用 0 L L B l I = d

84稳恒磁场的高斯定理与安培环路定理 乐B.dl=ho∑I 闭合积分环路L的选择 .闭合环路L上磁感应强度大小处处相等,磁感 应强度方向处处沿着积分路径的切向。 ∮B.dl=∮+Bdl=±Bd b.部分路径L磁感应强度大小处处相等,方向 处处沿着路径的切向。其余路径L2上磁感应强 度处处沿着路径的法向(或磁感应强度为零)。 fB.dl=B.dl+,B.dl=±Bdl=±Bdl 前页后页目录
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 7 闭合积分环路L的选择 a.闭合环路L上磁感应强度大小处处相等,磁感 应强度方向处处沿着积分路径的切向。 L B l d b.部分路径L1磁感应强度大小处处相等,方向 处处沿着路径的切向。其余路径L2上磁感应强 度处处沿着路径的法向(或磁感应强度为零)。 L = B l d L = B l d L B l d L1 = B l d L2 + B l d L1 = B l d L1 = B l d 0 L L B l I = d

8,4稳恒磁场的高斯定理与安培环路定理 ∮LBdi=o∑1 条件:电流分布具有特殊对称性,磁场也具有特殊 对称性,有可能用安培环路定理求得B。 关键:已知磁场的对称性,选择合适的积分环路。 求出等式左边的积分。 几个典型问题: 1)载流长直圆柱形导线内外的磁场 2)载流长直螺线管内的磁场 3)载流螺绕环内的磁场 前页后页目录 8
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 8 条件:电流分布具有特殊对称性,磁场也具有特殊 对称性,有可能用安培环路定理求得B。 关键:已知磁场的对称性,选择合适的积分环路。 求出等式左边的积分。 0 L L B l I = d 几个典型问题: 1)载流长直圆柱形导线内外的磁场 2)载流长直螺线管内的磁场 3)载流螺绕环内的磁场
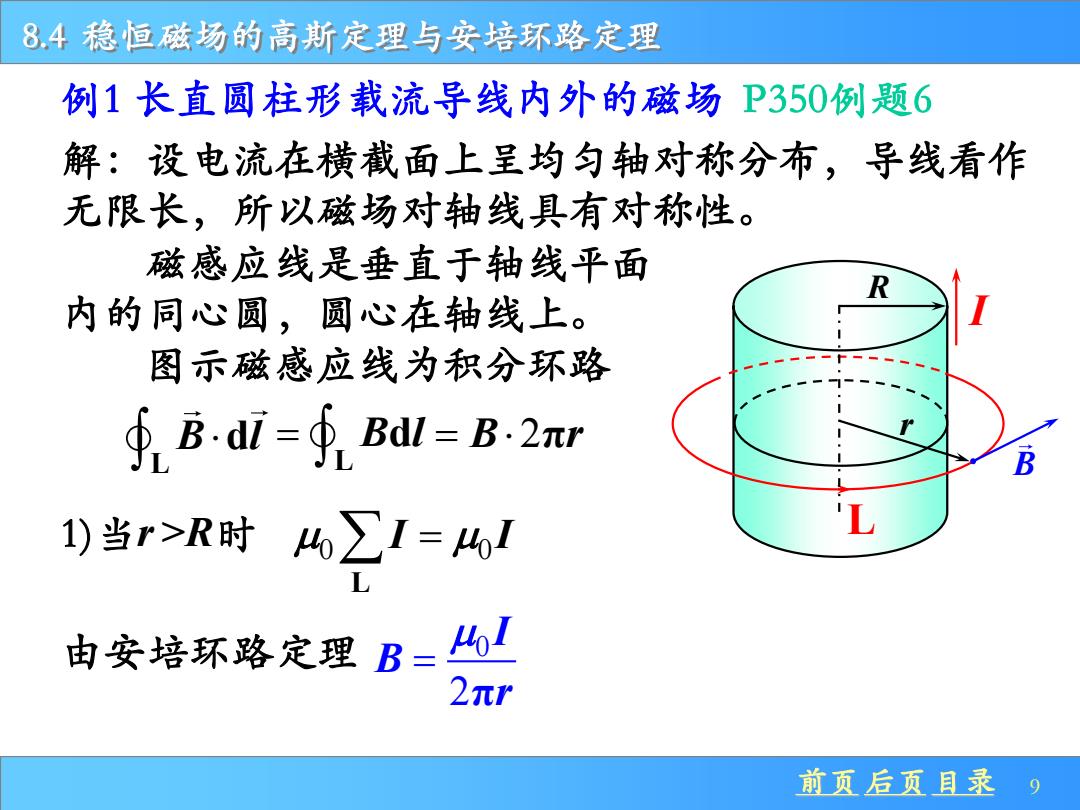
8.4稳恒磁场的高斯定理与安培环路定理 例1长直圆柱形载流导线内外的磁场P350例题6 解:设电流在横截面上呈均匀轴对称分布,导线看作 无限长,所以磁场对轴线具有对称性。 磁感应线是垂直于轴线平面 内的同心圆,圆心在轴线上。 图示磁感应线为积分环路 ∮B.dl=∮Bd=B.2πr 1)当r>R时4∑I=41 由安培环路定理B=l 2π 前页后页目录9
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 9 例1 长直圆柱形载流导线内外的磁场 P350例题6 I R r L 解:设电流在横截面上呈均匀轴对称分布,导线看作 无限长,所以磁场对轴线具有对称性。 1)当r >R时 由安培环路定理 L B l d L = B l d = B r 2π 0 0 L I I = 0 2π I B r = B 图示磁感应线为积分环路 磁感应线是垂直于轴线平面 内的同心圆,圆心在轴线上

84稳恒磁场的高斯定理与安培环路定理 2)当r<R时 a.电流均匀分布在柱形导体表面 h∑1=0 L 由安培环路定理B=O b.电流均匀分布在导体横截面 L 由安培环路定理B=此 2πR2 前页后页目录 10
8.4 稳恒磁场的高斯定理与安培环路定理 前页 后页 目录 10 2)当r <R 时 由安培环路定理 B = 0 b.电流均匀分布在导体横截面 由安培环路定理 a.电流均匀分布在柱形导体表面 0 L I 0 L I 0 2 2π Ir B R = I R r L B = 0 2 0 2 π π I r R =