江苏大学：《大学物理》课程教学资源（PPT课件）第六章 热力学基础 6.6 熵 玻耳兹曼关系

6.6熵玻耳兹曼关系 6.6熵 玻耳兹曼关系 一.熵S （克劳修斯熵) 由卡诺循环效率 n=- -+22=T-T 2T 吸热为正，放热卫为负。 整理后 +2=0 TT 卡诺循环中，热量与温度之比的总和为零。 前页后页且录 1

前页 后页 目录 1 6.6 熵 玻耳兹曼关系 一. 熵 S 由卡诺循环效率 1 1 2 1 A Q Q Q Q  = + = 吸热 Q 为正，放热 Q 为负。 整理后 1 2 1 2 0 Q Q T T + = 卡诺循环中，热量与温度之比的总和为零。 （克劳修斯熵） 1 2 1 T T T − = 6.6 熵 玻耳兹曼关系

6.6熵玻耳兹曼关系 图中可逆循环由4个 等温过程和4个绝热过程 组成。 相当于3个卡诺循环 组成的。 有限个卡诺循环组 成的可逆循环有 前页后页目录 .2

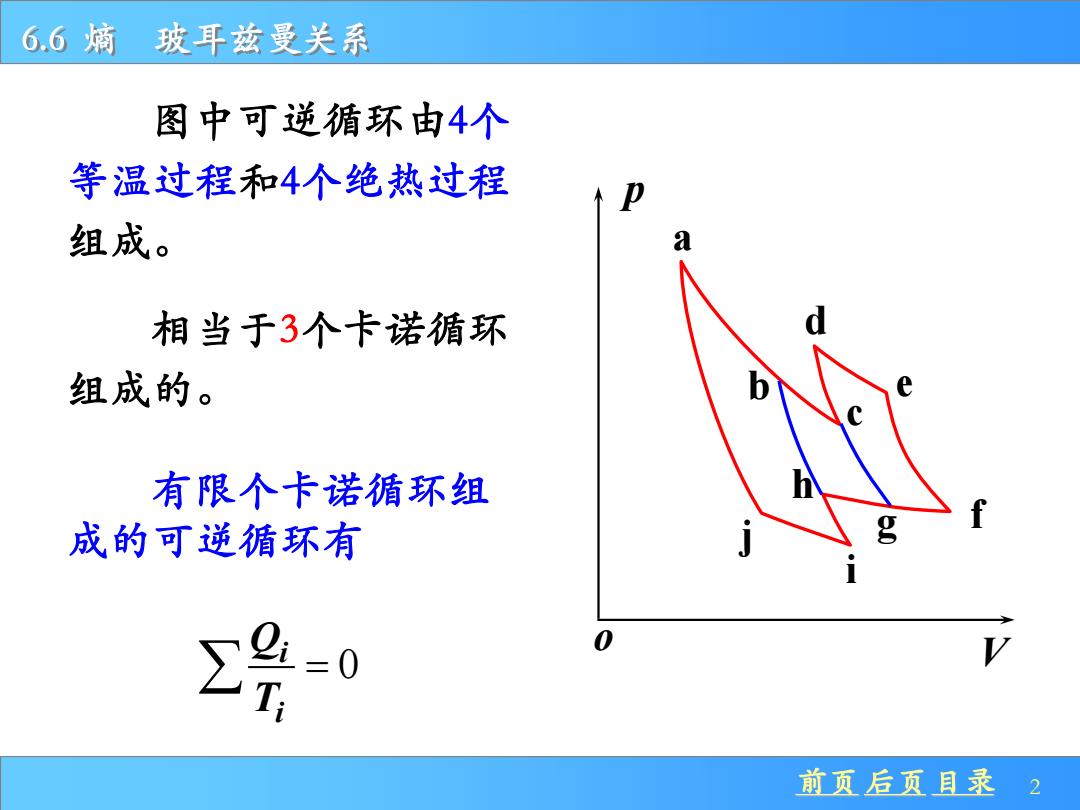
前页 后页 目录 2 6.6 熵 玻耳兹曼关系 有限个卡诺循环组 成的可逆循环有 p V o a c d e f h i j 图中可逆循环由4个 等温过程和4个绝热过程 组成。 b g 0 i i Q T  = 相当于3个卡诺循环 组成的

6.6嫡玻耳兹曼关系 任一可逆循环 看作由无限个（无穷 小的)卡诺循环组成的。 ims号0 写成积分式 0 dQ表示各无穷小等温过程中吸收的热量，积 分沿整个循环过程。 前页后页目录 3

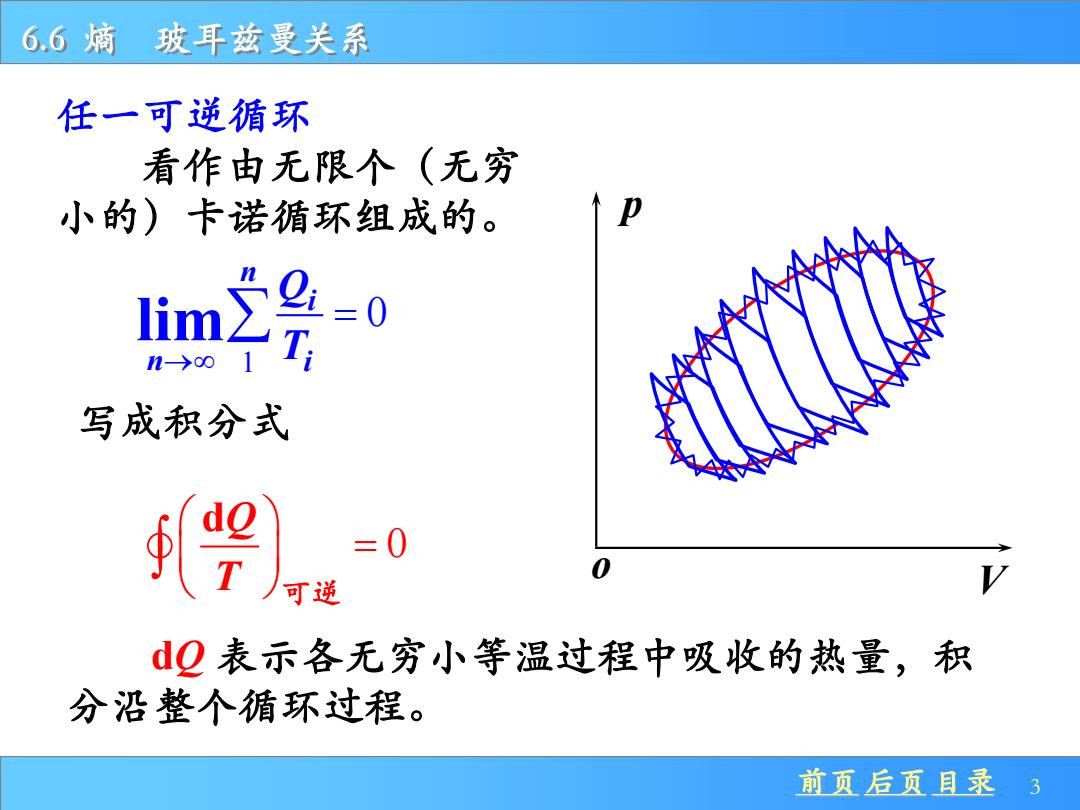
前页 后页 目录 3 6.6 熵 玻耳兹曼关系 任一可逆循环 看作由无限个（无穷 小的）卡诺循环组成的。 p V o 1 0 lim n i n i Q → T  = 写成积分式 0 dQ T   =      可逆 dQ 表示各无穷小等温过程中吸收的热量，积 分沿整个循环过程

6.6熵 玻耳兹曼关系 对可逆循环1a2b1,有 9 =0 可逆 即 （鸭)t+n吗)a=0 或 9)9)0 前页后页且录 4

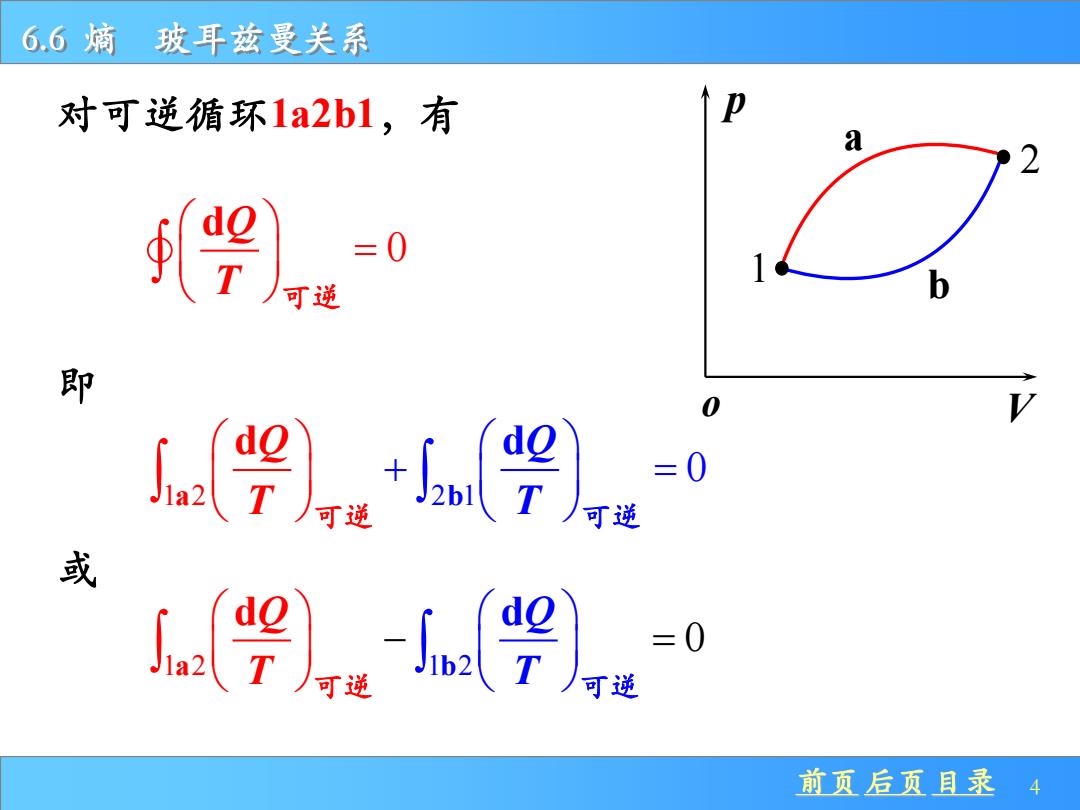
前页 后页 目录 4 6.6 熵 玻耳兹曼关系 对可逆循环1a2b1，有 0 dQ T   =      可逆 p o V 1 2 a b 即 1 2 2 1 0 a b dQ d T T   Q + =             可逆 可逆 或 1 2 1 2 0 a b d d T Q T   Q           − =   可逆 可逆

6.6熵玻耳兹曼关系 (S2 a 可 数分 的值与过程无 (S) 6 可游 关，只与始末两个状态有关。 定义状态函数S,称为熵。 的增亚为$=吗 可逆 前页后页目录5

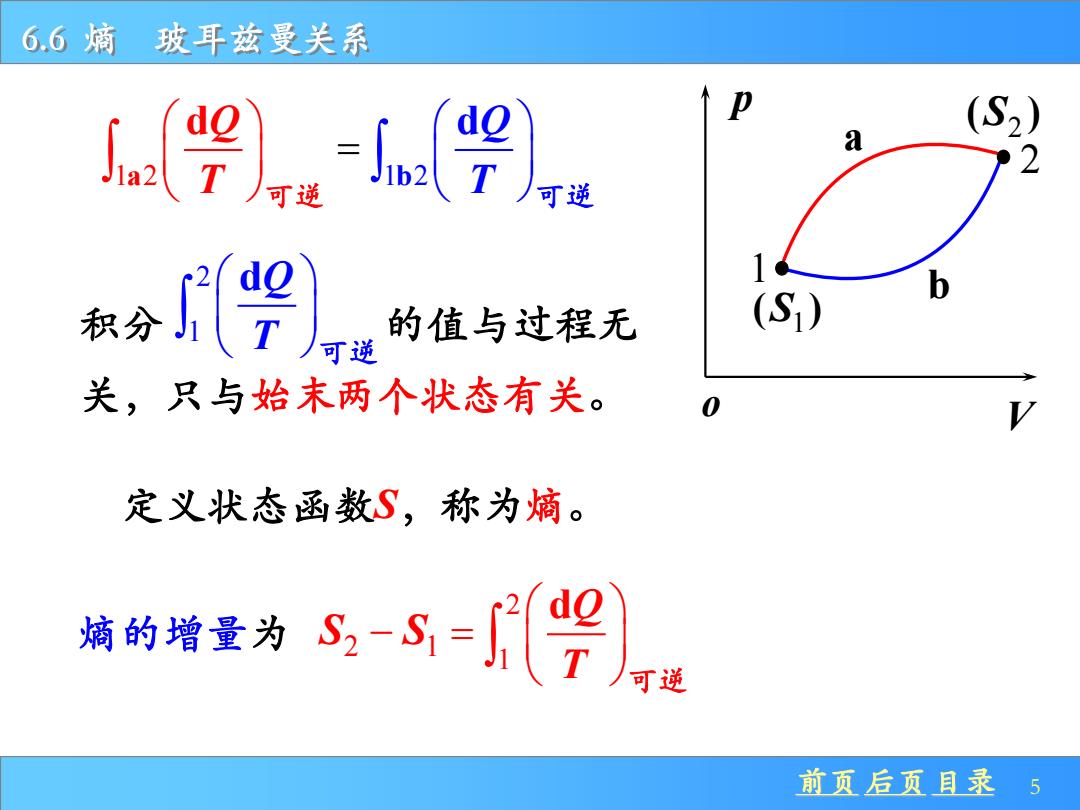
前页 后页 目录 5 6.6 熵 玻耳兹曼关系 1 2a 1b2 d dQ T Q T =               可逆 可逆 积分 的值与过程无 关，只与始末两个状态有关。 2 1 dQ T        可逆 p o V 1 2 a b 1 ( ) S 2 ( ) S 定义状态函数S，称为熵。 熵的增量为 S S 2 1 − 2 1 dQ T   =      可逆

6.6嫡玻耳兹曼关系 无穷小可逆过程的熵变 准静态绝热过程是等熵过程。 do do=0 =0 可逆 系统平衡态时的状态参量有体积、压强和温 度，现在又有一个熵。 前页后页目录 6

前页 后页 目录 6 6.6 熵 玻耳兹曼关系 无穷小可逆过程的熵变 d d Q S T   =    可逆 准静态绝热过程是等熵过程。 dQ = 0 0 d d Q S T   = =    可逆 系统平衡态时的状态参量有体积、压强和温 度，现在又有一个熵

6.6嫡玻耳兹曼关系 不可逆过程熵的增量计算 S2-S 不可逆 假想一个可逆过程计算熵的增量 可逆 前页后页目录 7

前页 后页 目录 7 6.6 熵 玻耳兹曼关系 2 2 1 1 dQ S S T   −       不可逆 不可逆过程熵的增量计算 假想一个可逆过程计算熵的增量 2 2 1 1 dQ S S T   − =      可逆

6.6熵玻耳兹曼关系 二.绝热自由膨胀的不可逆性 P1,,T 绝热自由膨胀的熵变 假想系统从初状态1准静态等 温变到终状态2，这个过程的熵变 与绝热自由膨胀相同。所以 P22V2,T S- 2 m RT dV m 绝热自由膨胀熵增加了。 不可逆过程熵一定增加？ 前页后页目录8

前页 后页 目录 8 6.6 熵 玻耳兹曼关系 二. 绝热自由膨胀的不可逆性 2 1 1 2 dQ S S T − =等温  2 1 p Vd T =  2 1 V d V m RT V M V T =  2 1 ln m V R M V = 绝热自由膨胀熵增加了。 不可逆过程熵一定增加？ 绝热自由膨胀的熵变 假想系统从初状态1准静态等 温变到终状态2，这个过程的熵变 与绝热自由膨胀相同。所以 1 1 p V T , , 2 2 p V T ,

6.6嫡玻耳兹曼关系 绝热自由膨胀不可逆性的解释 b 以4个分子为例 'c d A B A 0 abed a b e d bed aed abd abe ab ac ad be bd ed B abed 0 bed acd abd abe a b c d cd bd be ad ac ab 状态数11 4 4 6 11 系统回到初始状态的概率为十六分之一。162 前页后页目录 9

前页 后页 目录 9 6.6 熵 玻耳兹曼关系 绝热自由膨胀不可逆性的解释 a b c d A B 以4个分子为例 0 abcd abcd 0 a b c d bcd acd abd abc bcd acd abd abc a b c d ab ac ad bc bd cd cd bd bc ad ac ab A B 状态数 1 1 4 4 6 系统回到初始状态的概率为十六分之一。 4 1 1 16 2 =

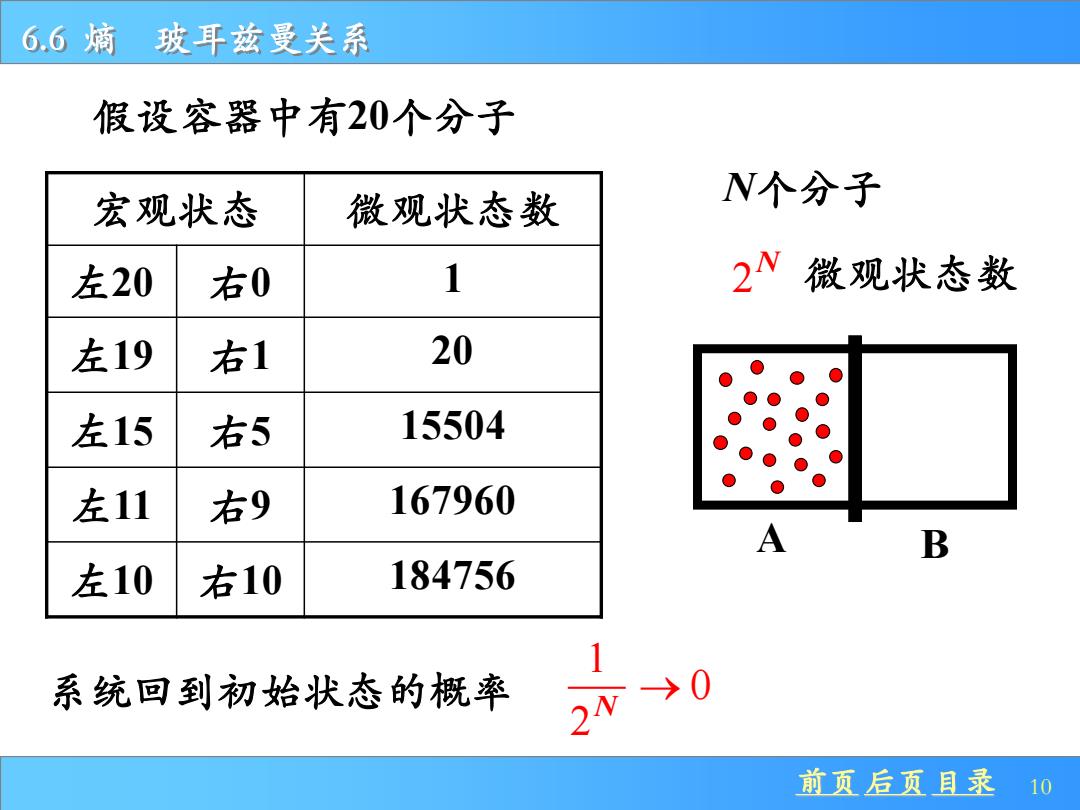
6.6熵玻耳兹曼关系 假设容器中有20个分子 宏观状态 微观状态数 N个分子 左20 右0 1 2V微观状态数 左19 右1 20 左15 右5 15504 左11 右9 167960 B 左10 右10 184756 系统回到初始状态的概率 →0 前页后页目录 10

前页 后页 目录 10 6.6 熵 玻耳兹曼关系 假设容器中有20个分子 A B 宏观状态 微观状态数 左20 右0 1 左19 右1 20 左15 右5 15504 左11 右9 167960 左10 右10 184756 2 N 1 2 系统回到初始状态的概率 N → 0 N个分子 微观状态数