5.4能量均分定理理想气体内能 5.4能量均分定理 理想气体内能 一.分子自由度 确定分子位置的独立坐标数。 分为平动、转动和振动自由度。 (1)单原子分子 ·(x,,z) 平动自由度=3 y 前页后页目录 1
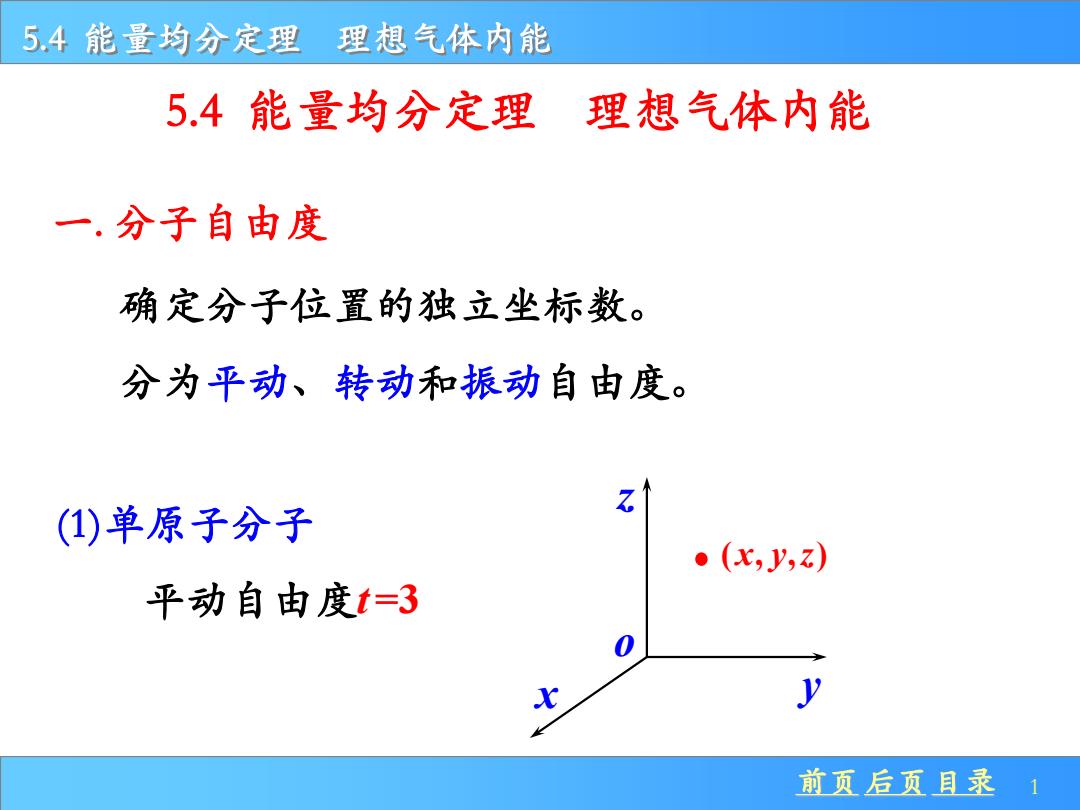
前页 后页 目录 1 5.4 能量均分定理 理想气体内能 一. 分子自由度 确定分子位置的独立坐标数。 分为平动、转动和振动自由度。 x y z o ( , , ) x y z (1)单原子分子 平动自由度t =3 5.4 能量均分定理 理想气体内能

5.4能量均分定理理想气体内能 (②)刚性双原子分子 B 平动自由度t=3 A(x,y,2) 转动自由度r=2 振动自由度5=0 y (3)非刚性双原子分子 (④)刚性多原子分子 平动自由度t=3 平动自由度t=3 转动自由度r=2 转动自由度r=3 振动自由度s=1 振动自由度5=0 前页后页目录 2
前页 后页 目录 2 5.4 能量均分定理 理想气体内能 (2)刚性双原子分子 x y z o A ( , , ) x y z B (3)非刚性双原子分子 平动自由度t =3 转动自由度r =2 振动自由度s =0 平动自由度t =3 转动自由度r =2 振动自由度s =1 (4)刚性多原子分子 平动自由度t =3 转动自由度r =3 振动自由度s =0

5.4能量均分定理理想气体内能 二.能量均分定理 -123 ekt=-,0= k7 2 ,@++)=7 2 气体分子在每一个平动自由度上具有相等的 平均平动动能,其大小等于二分之一kT。 前页后页目录 3
前页 后页 目录 3 5.4 能量均分定理 理想气体内能 二. 能量均分定理 2 0 1 3 2 2 kt = = m kT v 2 2 2 0 1 3 2 2 m kT ( ) v v v x y z + + = 2 0 1 1 2 2 m kT vx = 气体分子在每一个平动自由度上具有相等的 平均平动动能,其大小等于二分之一kT

5.4能量均分定理理想气体内能 能量按自由度均分定理 在温度为T的平衡态下,气体分子每一个自由 度的平均动能为。kT 2 分子平均平动动能4=号kT 分子平均转动动能4r=号kT 2 前页后页目录4
前页 后页 目录 4 5.4 能量均分定理 理想气体内能 能量按自由度均分定理 1 2 kT 在温度为T的平衡态下,气体分子每一个自由 度的平均动能为 分子平均平动动能 2 kt = t kT 分子平均转动动能 2 kr = r kT

5.4能量均分定理理想气体内能 分子平均振动动能4=kT t+r+skT 分子平均动能6=2 分子平均振动势能=kT 分子平均能量G=kT i=什r+2s,称为能量自由度 前页后页目录 5
前页 后页 目录 5 5.4 能量均分定理 理想气体内能 分子平均振动动能 2 ks s = kT 分子平均动能 2 + + k = t r s kT 分子平均振动势能 2 ps = s kT 分子平均能量 2 = i kT i =t+r+2s,称为能量自由度

54能量均分定理理想气体内能 三.理想气体的内能 气体分子热运动能量的总和。 F= mNAkT M E= m i RT M2 理想气体的内能只是温度的单值函数。 本节完 前页后页目录 6
前页 后页 目录 6 5.4 能量均分定理 理想气体内能 三. 理想气体的内能 气体分子热运动能量的总和。 2 = A m i E N kT M 2 = m i E RT M 理想气体的内能只是温度的单值函数。 本节完