
4.1狭义相对论基本原理洛伦兹变换 4.1狭义相对论基本原理 洛伦兹变换 以太 充满宇宙的假想物质。 迈克尔孙一莫雷实验 用于证明以太存在的实验。 实验结果:干涉条纹没有移动,证明以太不 存在。 前页后页目录1
前页 后页 目录 1 4.1 狭义相对论基本原理 洛伦兹变换 以太 充满宇宙的假想物质。 迈克尔孙—莫雷实验 用于证明以太存在的实验。 实验结果:干涉条纹没有移动,证明以太不 存在。 4.1 狭义相对论基本原理 洛伦兹变换

4.1狭义相对论基本原理洛伦兹变换 一.狭义相对论基本原理 (1)相对性原理 物理规律在一切惯性参考系中都具有相同的数 学表达形式。 例如:动量守恒定律 K系中m01+2i2=mo010+m2o⑦20 K'系中m+m5d2=mo0+mo20 (2)光速不变原理 一切惯性系中,光在真空中的速率都相等。 c=3×108m/s 前页后页目录2
前页 后页 目录 2 4.1 狭义相对论基本原理 洛伦兹变换 一. 狭义相对论基本原理 (1)相对性原理 物理规律在一切惯性参考系中都具有相同的数 学表达形式。 (2)光速不变原理 一切惯性系中,光在真空中的速率都相等。 例如:动量守恒定律 m m m m 1 1 2 2 10 10 20 20 v v v v + = + m m m m 1 1 2 2 10 10 20 20 v v v v + = + 8 c = 3 10 m/s K系中 K 系中

4.1狭义相对论基本原理洛伦兹变换 牛顿力学 时间 长度 与参照系无关 质量 速度、加速度与参照系有关 狭义相对论 时间 长度 与参照系有关 量 前页后页且录3
前页 后页 目录 3 4.1 狭义相对论基本原理 洛伦兹变换 牛顿力学 时间 长度 质量 与参照系无关 速度、加速度与参照系有关 狭义相对论 时间 长度 质量 与参照系有关
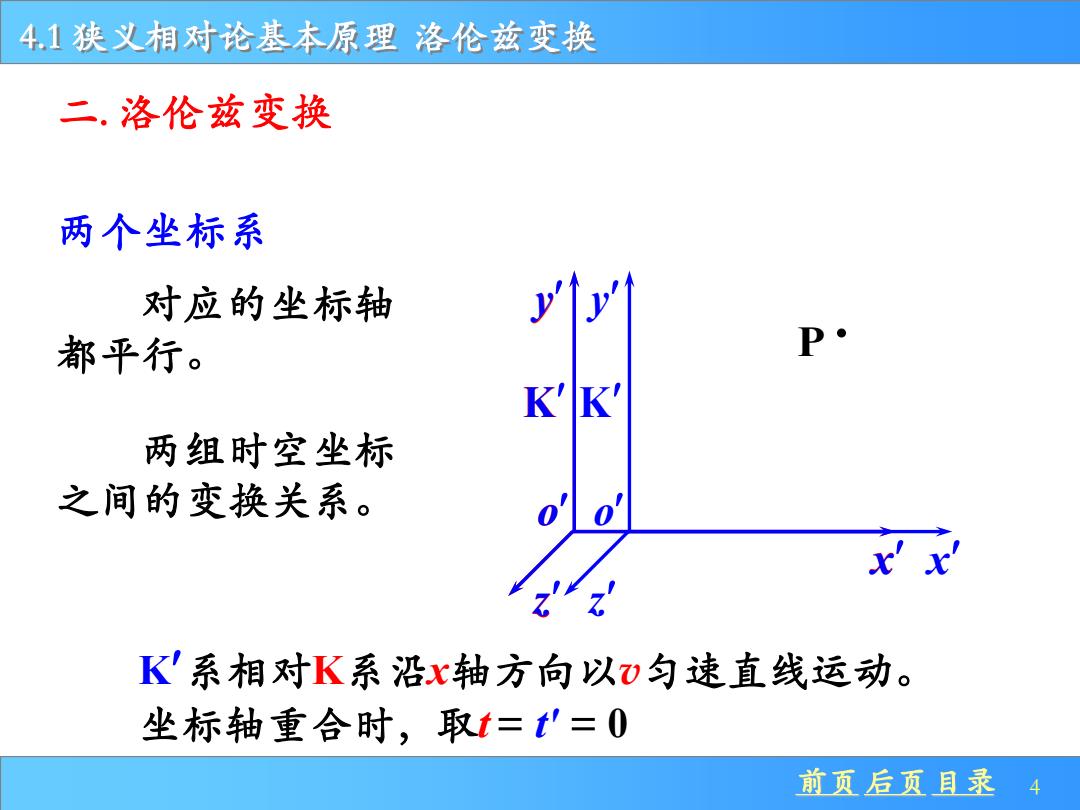
4.1狭义相对论基本原理洛伦兹变换 二.洛伦兹变换 两个坐标系 对应的坐标轴 y 都平行。 P KK' 两组时空坐标 之间的变换关系。 xx K'系相对K系沿x轴方向以)匀速直线运动。 坐标轴重合时,取t=t'=0 前页后页目录4
前页 后页 目录 4 4.1 狭义相对论基本原理 洛伦兹变换 K x y o z x K y o z x K y o z 两个坐标系 坐标轴重合时,取t = t' = 0 K系相对K系沿x轴方向以v匀速直线运动。 两组时空坐标 之间的变换关系。 P 二. 洛伦兹变换 对应的坐标轴 都平行

4.1狭义相对论基本原理洛伦兹变换 某时刻,质点P在两个坐标系中的描述 K (x,y,,) y P u,a,p K K K' (x,y,z,t) X u,a,p 前页后页目录5
前页 后页 目录 5 4.1 狭义相对论基本原理 洛伦兹变换 K x y o z x K y o z v 某时刻,质点P在两个坐标系中的描述 r K ( x y z t , , , ) u a p , , K ( x y z t , , , ) u a p , , P r

4.1狭义相对论基本原理洛伦兹变换 假想实验: 仁t'=0时,0和0' 重合,此时此地发出 一闪光。 某时刻光传到P 点。时空坐标 P(x,,z,) P(x,y,z,t) 因为oP≠0P,由光速不变原理,所以t≠t' 即时间是相对的。 前页后页目录6
前页 后页 目录 6 4.1 狭义相对论基本原理 洛伦兹变换 r 假想实验: t=t'=0时,o和o' 重合,此时此地发出 一闪光。 P , , , ( x y z t) P , , , ( x y z t ) 因为oP o'P K x y o z r 某时刻光传到P 点。时空坐标 ,由光速不变原理,所以 t t' 即时间是相对的。 x K y o z P

4.1狭义相对论基本原理洛伦兹变换 洛伦兹变换 x-vt x'+ut' x'= x= 7 c4 y=y J=y' 正变换 逆变换 z′=7 7=z t- x'←今x t'+ t t←>tt= 0←→一) 前页后页目录7
前页 后页 目录 7 4.1 狭义相对论基本原理 洛伦兹变换 正变换 逆变换 洛伦兹变换 x x v v − 2 2 2 2 2 1 1 x t x c y y z z t x c t c v v v v − = − = = − = − 2 2 2 2 2 1 1 x t x c y y z z t x c t c v v v v + = − = = + = − t t

4.1狭义相对论基本原理洛伦兹变换 讨论: x-vt X'= 1)t'与x、v、t均有关 72 2 2))C变换无意义,w的极限为C z′=z t- 2七 t' 本节完 前页后页且录8
前页 后页 目录 8 4.1 狭义相对论基本原理 洛伦兹变换 讨论: 1) t'与x、v 、t 均有关 2) v c 变换无意义, v的极限为c 本节完 2 2 2 2 2 1 1 x t x c y y z z t x c t c − = − = = − = − v v v v