
1.4牛顿运动定律 1.4牛顿运动定律 一.牛顿第一定律 任何物体都保持静止或匀速直线运动的状态, 直到作用在它上面的力迫使它改变这种状态为止。 惯性 物体保持原有运动状态不变的特性。 前页后页目录 1
前页 后页 目录 1 1.4 牛顿运动定律 一. 牛顿第一定律 任何物体都保持静止或匀速直线运动的状态, 直到作用在它上面的力迫使它改变这种状态为止。 惯性 物体保持原有运动状态不变的特性。 1.4 牛顿运动定律

1.4牛顿运动定律 二.牛顿第二定律 物体受到外力作用时,它所获得的加速度的大小 与外力的大小成正比,并与物体的质量成反比,加 速度的方向与外力的方向相同。 F ma SI制:N,kg,m/s2 讨论: 1)质量是惯性的量度。 2)瞬时性。 3)矢量性。 前页后页目录2
前页 后页 目录 2 1.4 牛顿运动定律 二. 牛顿第二定律 物体受到外力作用时,它所获得的加速度的大小 与外力的大小成正比,并与物体的质量成反比,加 速度的方向与外力的方向相同。 F ma = SI制:N,kg,m/s2 讨论: 1)质量是惯性的量度。 2)瞬时性。 3)矢量性

1.4牛顿运动定律 1.力的叠加原理(力的独立作用原理) 几个力同时作用在同一个物体上,物体产生的加速 度等于每个力单独作用时产生的加速度的失量和。也 等于这几个力的合力所产生的加速度。 ∑F=F+E+… F=md F2 maz ∑E=ma d=d1+d2+… 前页后页且录3
前页 后页 目录 3 1.4 牛顿运动定律 1.力的叠加原理(力的独立作用原理) 几个力同时作用在同一个物体上,物体产生的加速 度等于每个力单独作用时产生的加速度的矢量和。也 等于这几个力的合力所产生的加速度。 F ma 1 1 = F ma 2 2 = 1 2 a a a = + + F ma i = F F F i = + + 1 2

1.4牛顿运动定律 ∑E=ma 2.分量式 直角坐标系 自然坐标系 ∑Fe=max ∑F,=ma, ∑F=ma, ∑Fn=man ∑F:=maz ∑F2=0 前页后页目录4
前页 后页 目录 4 1.4 牛顿运动定律 2.分量式 直角坐标系 F ma x x = F ma y y = F ma z z = 自然坐标系 F ma t t = F ma n n = 0 Fz = F ma i =

1.4牛顿运动定律 ∑E=mi=m ∂ 3.牛顿第二定律的微分形式 D=mi F= dt dp Fdt 适用于变质量和高速运动。 前页后页目录5
前页 后页 目录 5 1.4 牛顿运动定律 p m= v 适用于变质量和高速运动。 3.牛顿第二定律的微分形式 d d p F t = d d p F t = d d F ma m i t = = v

1.4牛顿运动定律 三.牛顿第三定律 两个物体之间的作用力和反作用力沿同一直线, 大小相等,方向相反。分别作用在两个物体上。 F=-F 讨论:作用力和反作用力性质相同;同时出现、同时 消失,没有先后、主次之分。 惯性参照系:牛顿运动定律成立的参照系 相对于惯性系作匀速直线运动的参照 系都是惯性系。 前页后页目录
前页 后页 目录 6 1.4 牛顿运动定律 三. 牛顿第三定律 两个物体之间的作用力和反作用力沿同一直线, 大小相等,方向相反。分别作用在两个物体上。 F F = − 讨论:作用力和反作用力性质相同;同时出现、同时 消失,没有先后、主次之分。 惯性参照系:牛顿运动定律成立的参照系 相对于惯性系作匀速直线运动的参照 系都是惯性系

1.4牛顿运动定律 四.牛顿运动定律应用举例 两类基本问题 由运动方程求力下→⑦→石→F导数运算 由力求运动方程F→石→⑦→下积分运算 解题的一般步骤 1)理解题意,确定研究对象 2)隔离体法分析受力,画受力图 3)建立坐标系,列方程 4)解方程,讨论 前页后页目录7
前页 后页 目录 7 1.4 牛顿运动定律 两类基本问题 由力求运动方程 由运动方程求力 解题的一般步骤 1)理解题意,确定研究对象 2)隔离体法分析受力,画受力图 3)建立坐标系,列方程 4)解方程,讨论 四. 牛顿运动定律应用举例 r a F → → → v F a r → → →v 导数运算 积分运算
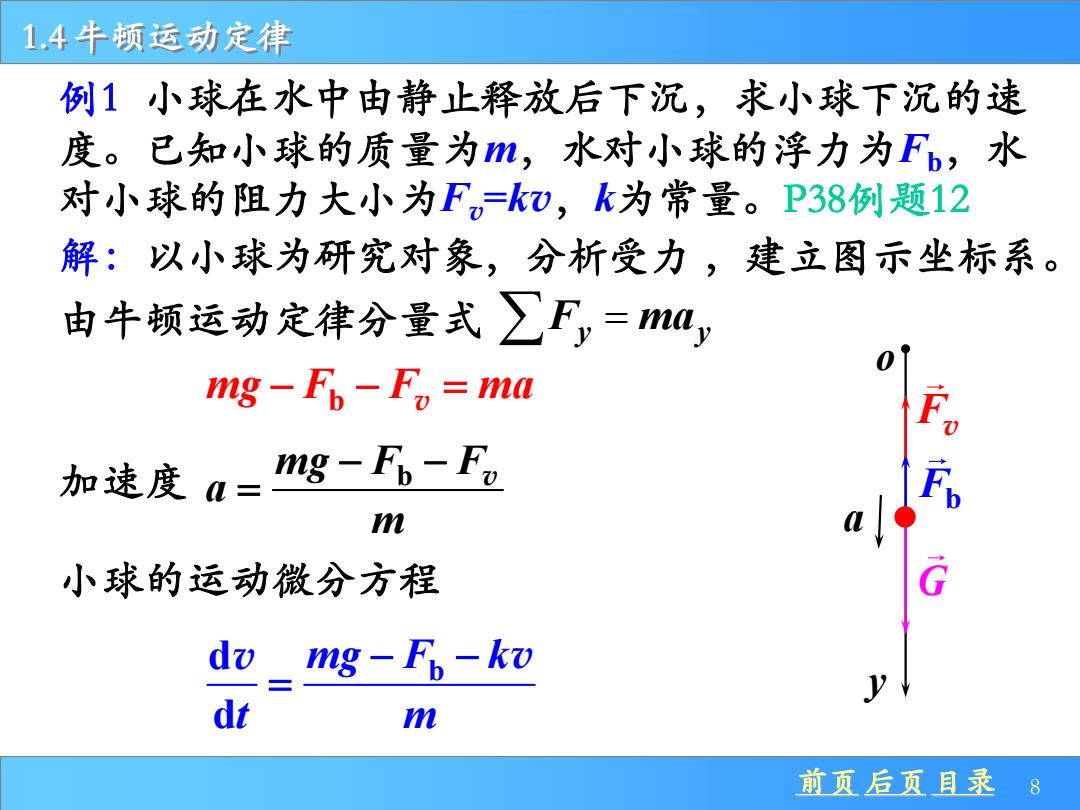
1.4牛顿运动定律 例1小球在水中由静止释放后下沉,求小球下沉的速 度。已知小球的质量为m,水对小球的浮力为Fb,水 对小球的阻力大小为F,=k),k为常量。P38例题12 解:以小球为研究对象,分析受力,建立图示坐标系。 由牛顿运动定律分量式∑F,=ma, mg-F-Fo ma 加速度a=g--F m 小球的运动微分方程 dv mg-Fp-ko dt m 前页后页且录8
前页 后页 目录 8 1.4 牛顿运动定律 例1 小球在水中由静止释放后下沉,求小球下沉的速 度。已知小球的质量为m,水对小球的浮力为Fb,水 对小球的阻力大小为Fv =kv,k为常量。P38例题12 解:以小球为研究对象,分析受力 Fb Fv G y o mg F F ma − − = b v 加速度 小球的运动微分方程 d b d mg F k t m − − = v v 由牛顿运动定律分量式 ,建立图示坐标系。 a F ma y y = mg F F b a m − − = v

1.4牛顿运动定律 do mg-F-ko dt m 令 mg-Fp k 则 dv k(UT-v) dt m do k 分离变量,得 dt (or-0) m 两边积分 。- 前页后页目录9
前页 后页 目录 9 1.4 牛顿运动定律 令 则 分离变量,得 d d ( ) T k t m = − v v v d ( ) d T k t m − = v v v 两边积分 d b d mg F k t m − − = v v b T mg F k − v = 0 0 d d t T k t m = − v v v v
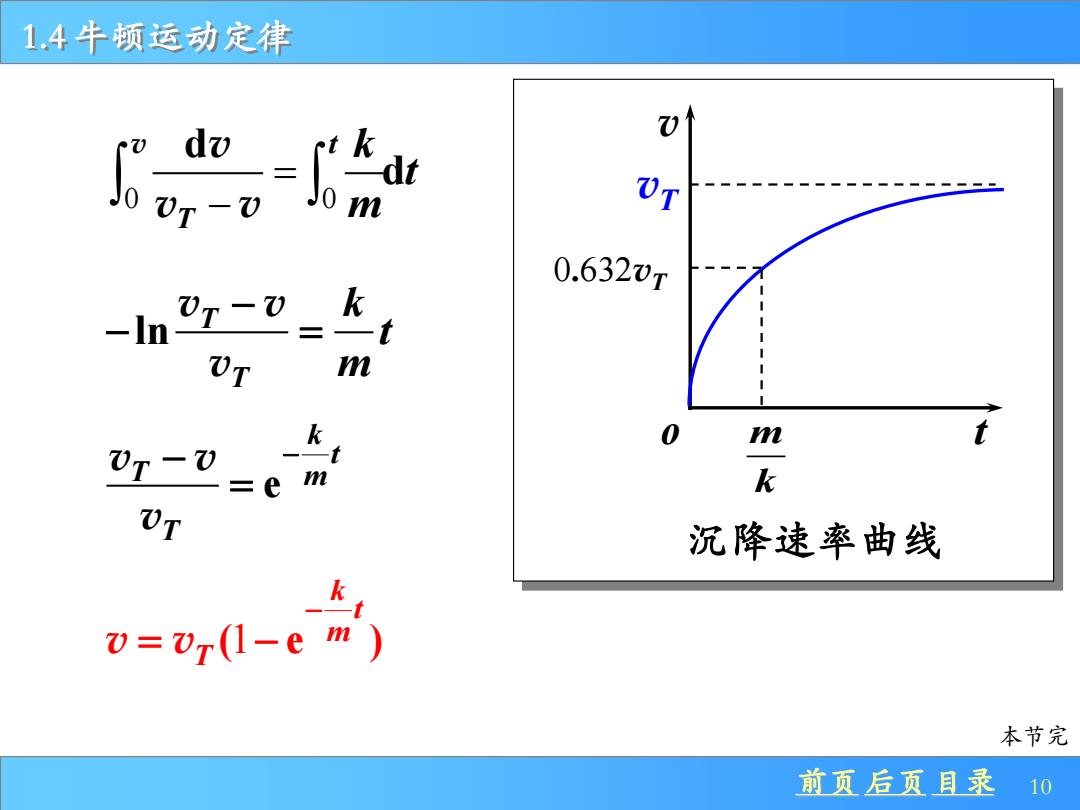
1.4牛顿运动定律 。 dv rt k Jo m UT 0.632wr UT-U k -In 1 VT m 0 m t e m k 01 沉降速率曲线 k 1 0=0r(1-em) 本节完 前页后页目录10
前页 后页 目录 10 1.4 牛顿运动定律 ln T T k t m − − = v v v ( e ) 1 k t m T − v v = − 沉降速率曲线 m k v vT 0 632 . vT o t 本节完 0 0 d d t T k t m = − v v v v e k t T m T − − = v v v