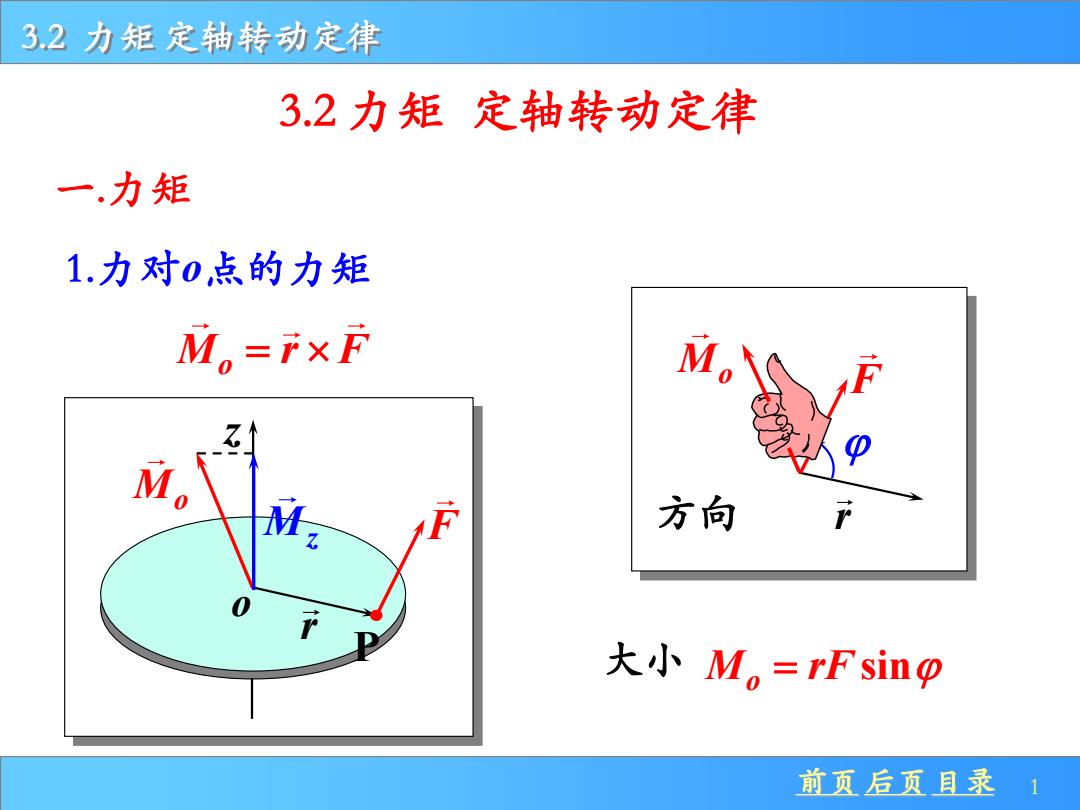
32力矩定轴转动定律 3.2力矩定轴转动定律 一.力矩 1.力对0,点的力矩 Mo=FxF M M。 方向 大小M。=rFsinp 前页后页目录1
前页 后页 目录 1 3.2 力矩 定轴转动定律 一.力矩 1.力对o点的力矩 M r F o = r Mo z o F P 大小 M rF o = sin 3.2 力矩 定轴转动定律 Mz r Mo 方向 F
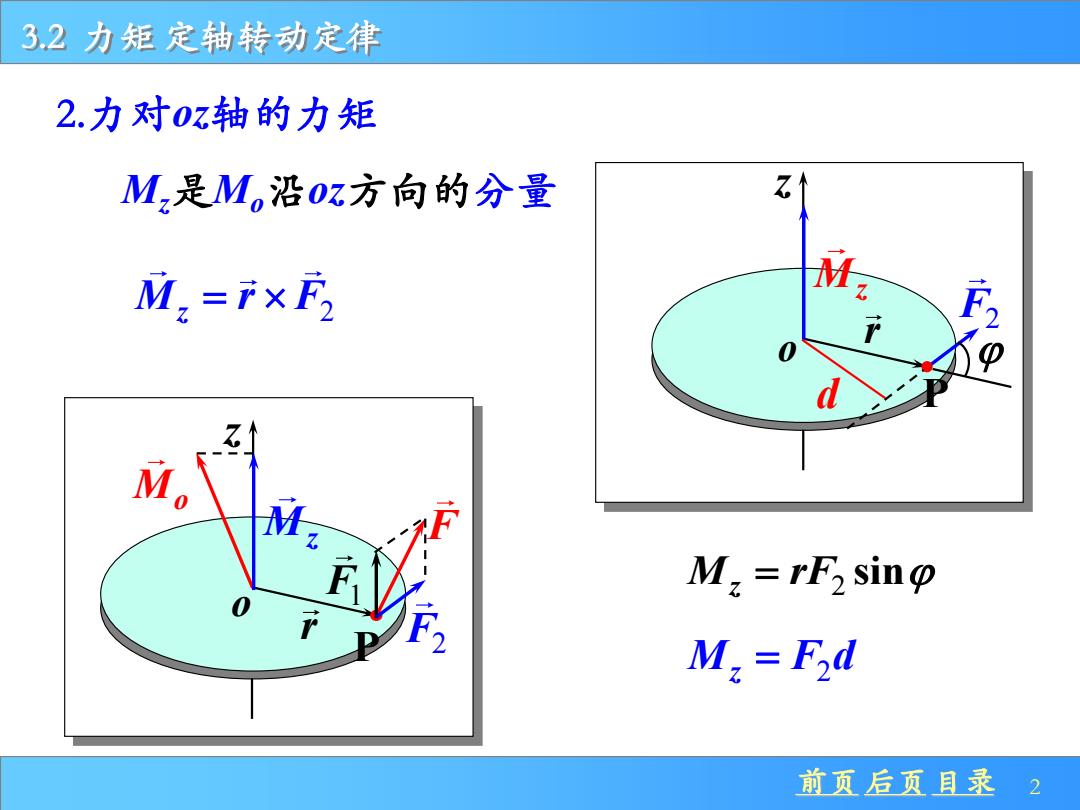
3:2力矩定轴转动定律 2.力对0z轴的力矩 M,是M,沿0z方向的分量 M2=F×F2 M。 M.rF2 sinp M,=F2d 前页后页目录2
前页 后页 目录 2 3.2 力矩 定轴转动定律 2.力对oz轴的力矩 M r F z = 2 r z Mz o F2 d P 2 M rF z = sin M F d z = 2 Mz是Mo沿oz方向的分量 r Mo z o F P Mz F2 F1

3:2力矩定轴转动定律 讨论: 1)零力矩条件 力平行于转轴或作用线通过转轴 2)十、-号表示方向 3)合力矩的计算 Mz=M1z+M2z+… 前页后页且录3
前页 后页 目录 3 3.2 力矩 定轴转动定律 讨论: 1)零力矩条件 力平行于转轴或作用线通过转轴 2)+、-号表示方向 3)合力矩的计算 1 2 ... M M M z z z = + +
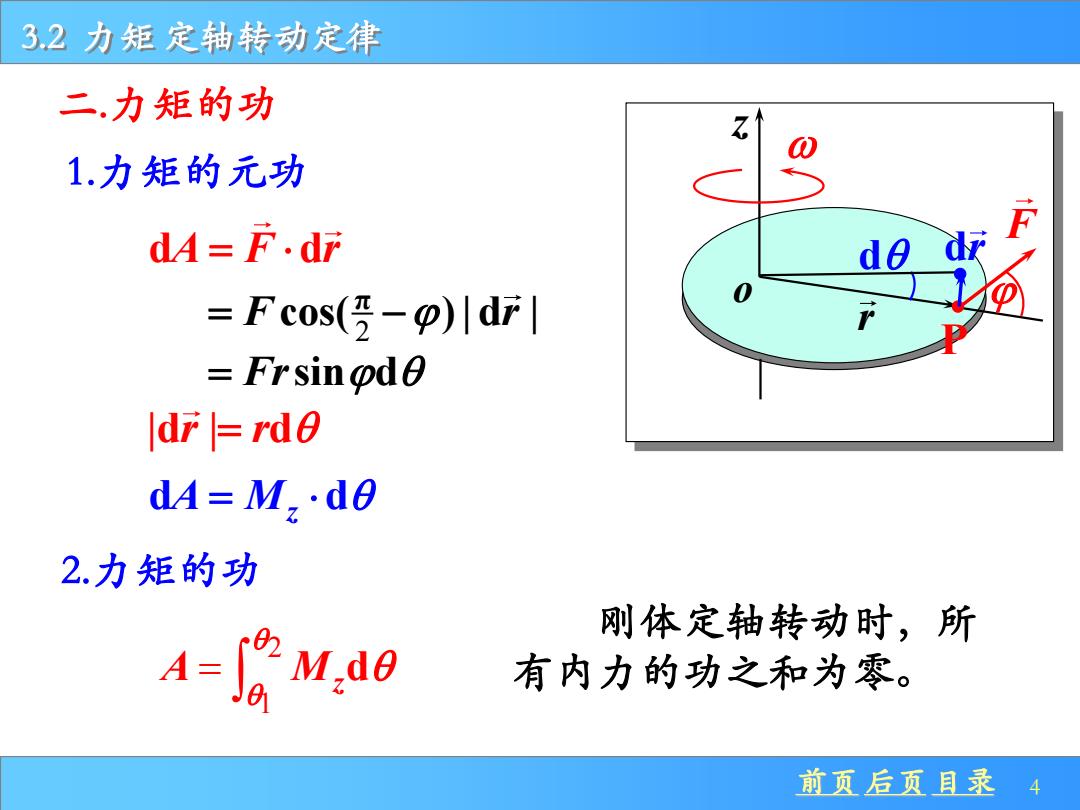
32力矩定轴转动定律 二.力矩的功 1.力矩的元功 dA=F.dr =Fcos(受-p)川dF| Frsinode ldr |rdo dA=M2·d0 2.力矩的功 4%na0 刚体定轴转动时,所 有内力的功之和为零。 前页后页目录4
前页 后页 目录 4 3.2 力矩 定轴转动定律 二.力矩的功 r z o F d dr P 1.力矩的元功 d d A F r = 2 π = − F r cos( ) | d | = Frsin d |d | d r r = d d A Mz = 2.力矩的功 2 1 A Mzd = 刚体定轴转动时,所 有内力的功之和为零
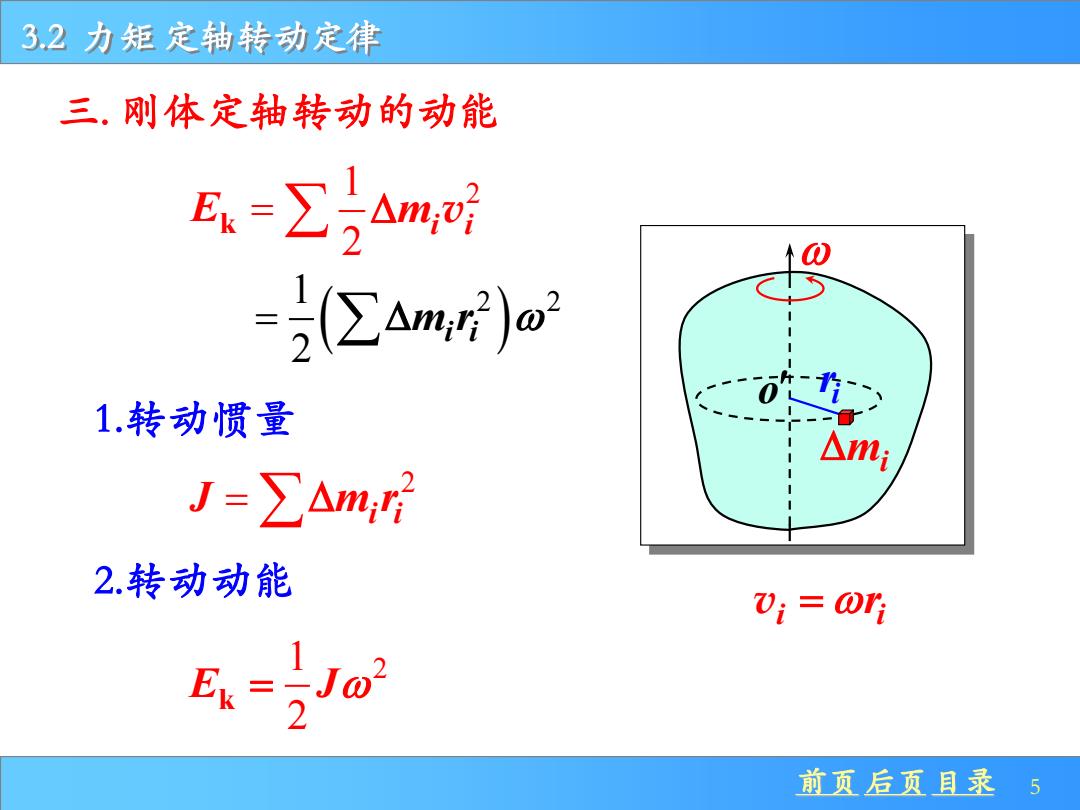
32力矩定轴转动定律 三.刚体定轴转动的动能 E=∑Am,时 =(∑ami)o 1.转动惯量 △mi J=∑△m, 2.转动动能 V:=0r Ex=-Jo2 2 前页后页目录5
前页 后页 目录 5 3.2 力矩 定轴转动定律 三. 刚体定轴转动的动能 Ek = ( ) 1 2 2 2 = m ri i 1.转动惯量 2 i i J m r = 2.转动动能 1 2 2 E J k = i r o mi 1 2 2 mi i v i i v = r
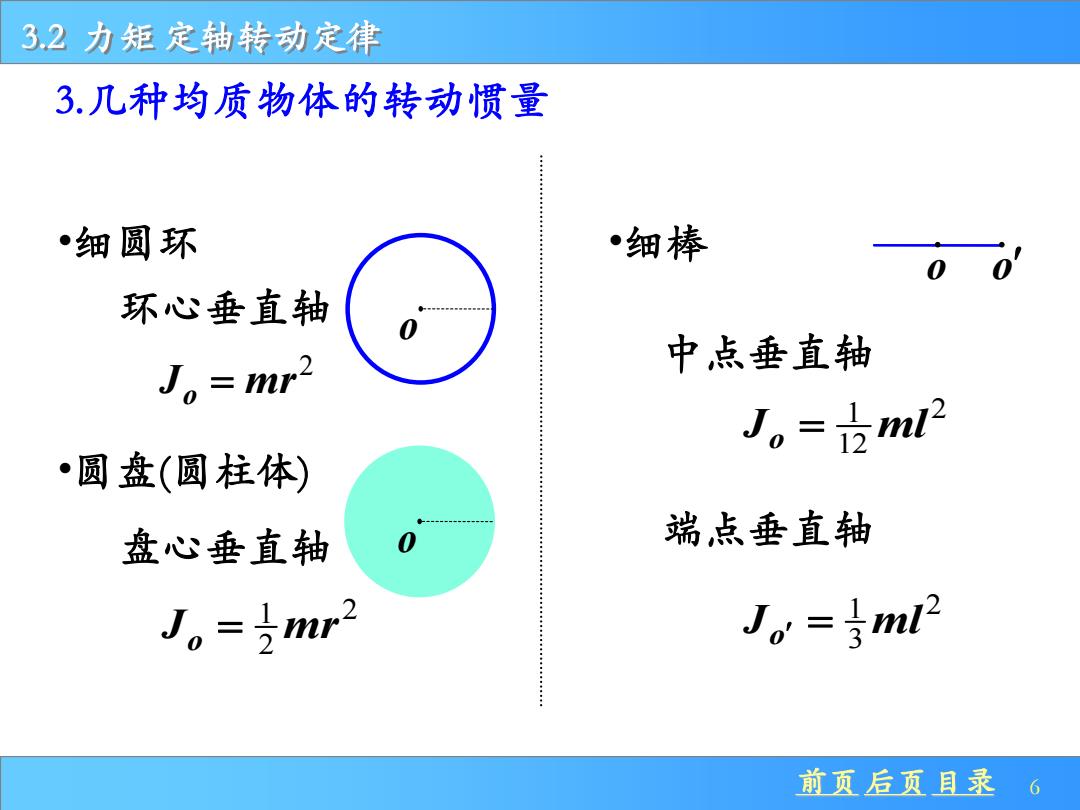
32力矩定轴转动定律 3.几种均质物体的转动惯量 •细圆环 •细棒 环心垂直轴 中点垂直轴 J。=mr2 Jo=ml2 •圆盘(圆柱体) 盘心垂直轴 端点垂直轴 Jo=mr2 Jo=ml2 前页后页目录6
前页 后页 目录 6 3.2 力矩 定轴转动定律 3.几种均质物体的转动惯量 2 o J mr = •细圆环 环心垂直轴 o 1 2 o 2 J mr = •圆盘(圆柱体) 盘心垂直轴 o •细棒 1 2 o 12 J ml = o 中点垂直轴 端点垂直轴 1 2 o 3 J ml = o

32力矩定轴转动定律 四.定轴转动的动能定理 由质点系动能定理 A外+A内=E2-Ek1 1.刚体定轴转动的动能定理 合外力矩对刚体所做的功等于刚体转动动能的 增量。 pM.d0-2Joi-2Joi 前页后页目录7
前页 后页 目录 7 3.2 力矩 定轴转动定律 四. 定轴转动的动能定理 由质点系动能定理 A A E E 外 + = − 内 k2 k1 合外力矩对刚体所做的功等于刚体转动动能的 增量。 2 2 2 2 1 1 1 1 2 2 M J J zd = − 1.刚体定轴转动的动能定理

32力矩定轴转动定律 五.刚体的重力势能 刚体的重力势能等于刚体上各质点重力势能之和 Ep=∑Am8a 体积不大时E。=g∑△my: ∑Amy_∑Amy 质心ye=∑Am: n Ep=mgye 一个体积不大的刚体的重力势能等于它 的质量集中在质心时所具有的重力势能。 前页后页目录 8
前页 后页 目录 8 3.2 力矩 定轴转动定律 五. 刚体的重力势能 刚体的重力势能等于刚体上各质点重力势能之和 体积不大时 质心 一个体积不大的刚体的重力势能等于它 的质量集中在质心时所具有的重力势能。 E g m y p = i i E m g y p = iii E mgy p c = c i i i m y y m = m yi i m =

32力矩定轴转动定律 六.刚体定轴转动定律 定轴转动刚体的角加速度与作用在刚体上的 合力矩成正比、与转动惯量成反比。 M a= 或M,=Ja J 转动惯量是刚体转动时惯性大小的量度。 这个定律可以由牛顿运动定律导出,仅适用 于惯性系。 前页后页目录9
前页 后页 目录 9 3.2 力矩 定轴转动定律 定轴转动刚体的角加速度与作用在刚体上的 合力矩成正比、与转动惯量成反比。 Mz J = 转动惯量是刚体转动时惯性大小的量度。 六. 刚体定轴转动定律 或 M J z = 这个定律可以由牛顿运动定律导出,仅适用 于惯性系
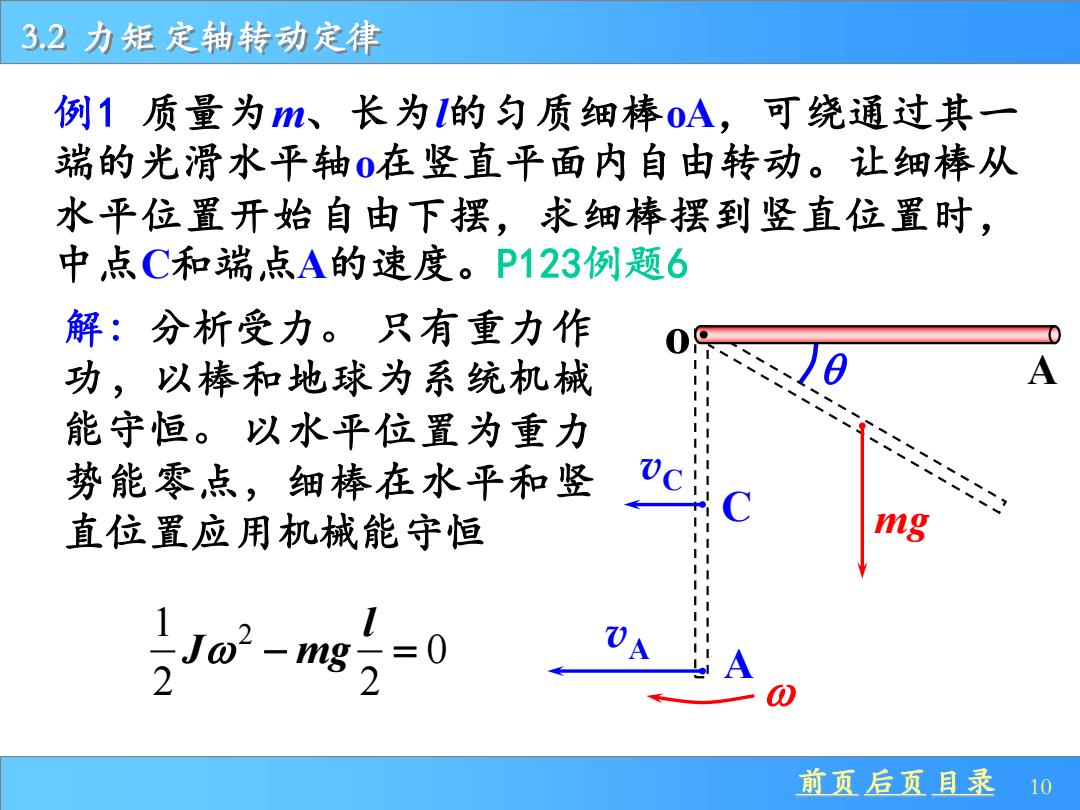
32力矩定轴转动定律 例1质量为m、长为l的匀质细棒0A,可绕通过其一 端的光滑水平轴0在竖直平面内自由转动。让细棒从 水平位置开始自由下摆,求细棒摆到竖直位置时, 中点C和端点A的速度。P123例题6 解:分析受力。只有重力作 功,以棒和地球为系统机械 A 能守恒。以水平位置为重力 势能零点,细棒在水平和竖 直位置应用机械能守恒 mg -号=0 前页后页目录10
前页 后页 目录 10 3.2 力矩 定轴转动定律 只有重力作 功,以棒和地球为系统机械 能守恒。 例1 质量为m、长为l的匀质细棒oA,可绕通过其一 端的光滑水平轴o在竖直平面内自由转动。让细棒从 水平位置开始自由下摆,求细棒摆到竖直位置时, 中点C和端点A的速度。P123例题6 C vC A o vA 解:分析受力。 mg A 以水平位置为重力 势能零点,细棒在水平和竖 直位置应用机械能守恒 1 2 0 2 2 l J mg − =