
第五章气体动理论 第五章气体动理论 1.理想气体状态方程 pV=RT p=nkT M 普适气体常数R=8.31J/(mol.K) 玻耳兹曼常量k= R=1.38×1023J/K N 分子数量密度n= V 前页后页且录 1
前页 后页 目录 1 第五章 气体动理论 1.理想气体状态方程 m pV RT M = p nkT = 普适气体常数 R = 8 31 . J/(mol K) 玻耳兹曼常量 分子数量密度 N n V = 23 1 38 10 A . J/K R k N − = = 第五章 气体动理论

第五章气体动理论 2.热力学温标 T=t+273.15 3.平均碰撞频率 Z=√2nmd2o 4.平均自由程 1 kT √2πd2n 元=2mdp 前页后页目录2
前页 后页 目录 2 第五章 气体动理论 2.热力学温标 T t = + 273 15 . 3.平均碰撞频率 2 Z n d = 2 π v 4.平均自由程 2 1 2πd n = 2 2π kT d p =

第五章气体动理论 5.理想气体的压强 2 p=nEkt p=nkT 3 6.分子平均平动动能 6= = T 2 前页后页目录3
前页 后页 目录 3 第五章 气体动理论 5.理想气体的压强 2 3 kt p n = 6.分子平均平动动能 2 0 1 1 1 2 kt N i i m N = = v 2 0 1 2 = m v 3 2 kt = kT p nkT =

第五章气体动理论 7温度的物理意义 T= 26t 3k 8.能量按自由度均分定理 在温度为T的平衡态下,气体分子每一个自由度 的平均动能为二kT 2 前页后页且录4
前页 后页 目录 4 第五章 气体动理论 7.温度的物理意义 2 3 kt T k = 8.能量按自由度均分定理 1 2 kT 在温度为T的平衡态下,气体分子每一个自由度 的平均动能为

第五章气体动理论 分子平均能量 i :二kT 2 i=什+2s,称为能量自由度 9.理想气体的内能 气体分子热运动能量的总和。 E= m i RT M2 前页后页目录5
前页 后页 目录 5 第五章 气体动理论 分子平均能量 2 i = kT i =t+r+2s,称为能量自由度 9.理想气体的内能 气体分子热运动能量的总和。 2 m i E RT M =

第五章气体动理论 10.速率分布函数(概率密度) 在)~w+d)内的分子数占总分子数的比率。 N f(v)dv dN f(w)= Ndo 物理意义:速率在)附近的单位速率区间内的分子 数占总分子数的比率。 或某一分子在速率)附近出现的概率。 前页后页目录
前页 后页 目录 6 第五章 气体动理论 在v~v+dv内的分子数占总分子数的比率。 dN N = f ( )d v v 10.速率分布函数(概率密度) d ( ) d N f N v = v 物理意义:速率在v附近的单位速率区间内的分子 数占总分子数的比率。 或某一分子在速率v附近出现的概率

第五章气体动理论 f(o) 速率在01~V2之间的 分子数占总分子数的 比率。 fouo △N N 0 V102 70 归一化条件:。f(o)do=l 前页后页目录7
前页 后页 目录 7 第五章 气体动理论 f ( ) v o v 速率在v1~v2之间的 分子数占总分子数的 比率。 2 1 ( )d N f N = v v v v v1 v2 归一化条件: 1 0 f ( )d = v v

第五章气体动理论 11.三种速率 2kT 2RT 最概然速率 0p= mo M 8kT 8RT 平均速率 V 元no 元M 3kT 3RT 方均根速率 mo M 前页后页目录8
前页 后页 目录 8 第五章 气体动理论 11.三种速率 最概然速率 0 2 p kT m v = 2RT M = 平均速率 0 8 π kT m v = 8 π RT M = 方均根速率 2 0 3kT m v = 3RT M =
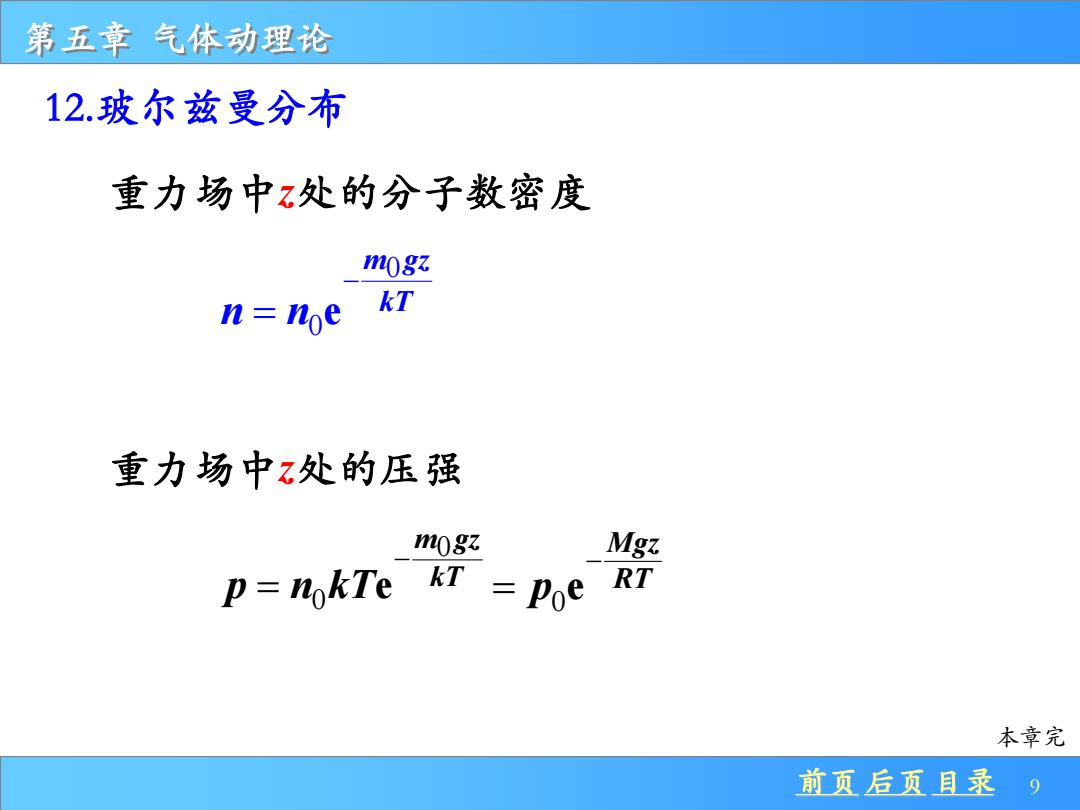
第五章气体动理论 12.玻尔兹曼分布 重力场中z处的分子数密度 mogz kT 重力场中z处的压强 mogz Mgz p=nokTe kT Poe RT 本章完 前页后页且录9
前页 后页 目录 9 第五章 气体动理论 12.玻尔兹曼分布 重力场中z处的分子数密度 0 0 e m gz kT n n − = 重力场中z处的压强 0 0 e m gz kT p n kT − = 0 e Mgz RT p − = 本章完