73静电场的高斯定理 7.3静电场的高斯定理 一.静电场的高斯定理 d 1.,点电荷在球心 平E=乐E-ds=求Eas 4元80r1 =9 E=9 e, 与球面半径无关 4π80r1 60 前页后页目录 1
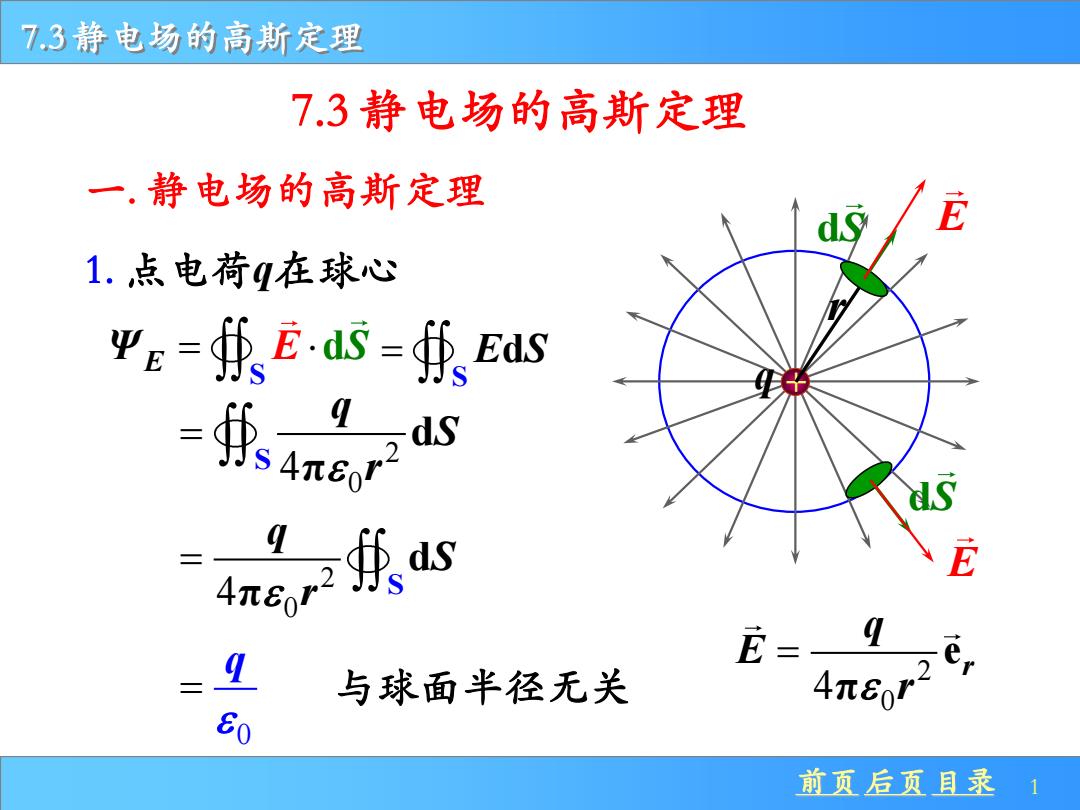
前页 后页 目录 1 7.3 静电场的高斯定理 q + 1. 点电荷q在球心 7.3 静电场的高斯定理 S ΨE = E dS S = E Sd 2 0 4 S d π q S r = 2 0 4 S d π q S r = 0 q = r dS E dS E 一. 静电场的高斯定理 2 0 4 e π r q E r = 与球面半径无关

73静电场的高斯定理 2.任意闭合曲面S包围点电荷q 平e=求Ed5-身 正点电荷q发出?条电场线。 60 3.闭合曲面S不包围,点电荷q 平e=求Ed心=0 前页后页且录2
前页 后页 目录 2 7.3 静电场的高斯定理 2. 任意闭合曲面S包围点电荷q S ΨE = E Sd + 3. 闭合曲面S不包围点电荷q S ΨE = E Sd q 正点电荷q发出 条电场线。 0 q 0 q = = 0
73静电场的高斯定理 4.闭合曲面S包围q1…qk,面外有qk+1…qn E=E+…+E+Ek1++E。 ds ΨE=求E-ds q1° ,k =求Ed++乐Eds 。q4n +求E1dS+乐E。·d ● ●qk+1 =1+…+4+0 Eo 60 东Eds=∑a 80S内 80S内 适用于任意带电体 前页后页目录3
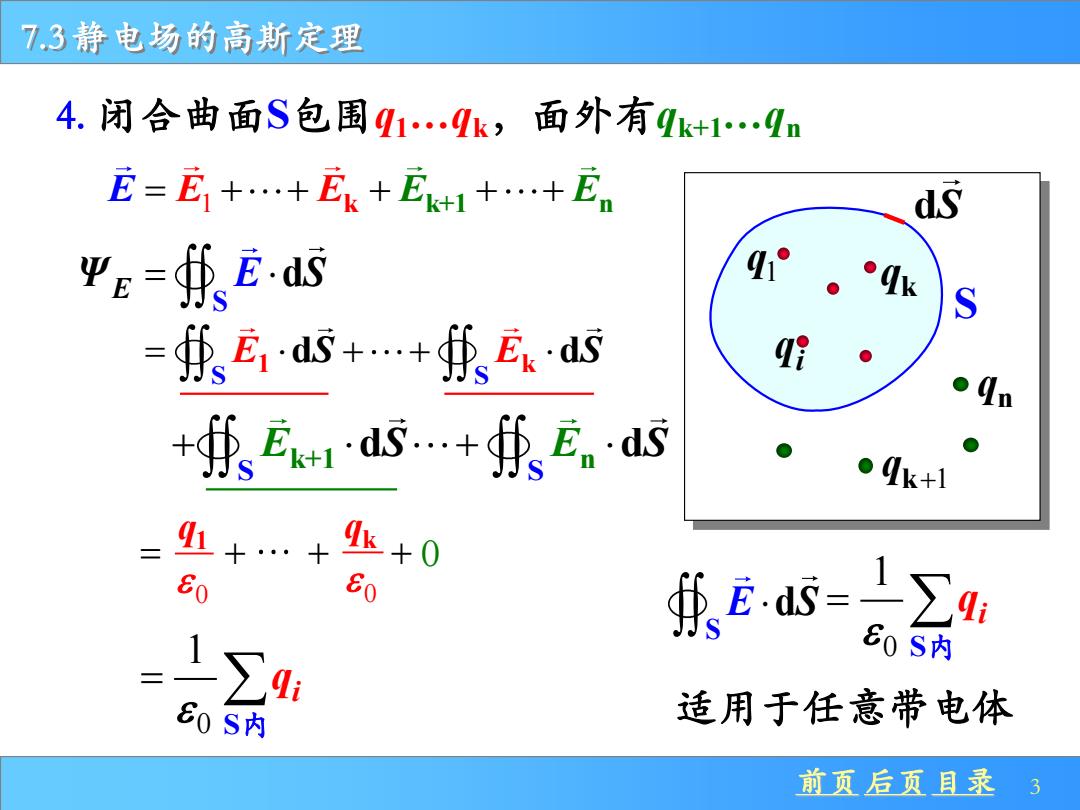
前页 后页 目录 3 7.3 静电场的高斯定理 S 1 q i q k q k 1 q + n q 4. 闭合曲面S包围q1…qk,面外有qk+1…qn S d E Ψ = E S 0 kq S S = + + E E 1 k d d S S 0 1 S i q = 内 k+ n S S + + E E 1 d d S S = + + + 0 1 q 0 E = + + + + + E E 1 k E E k+1 n dS S E dS 0 1 S i q = 内 适用于任意带电体

73静电场的高斯定理 高斯定理 在静电场中,通过任意闭合曲面的电通量, 等于该曲面内电荷量的代数和除以真空中的介电 常数。 E-as=∑m 80S内 闭合曲面S常称为高斯面。 高斯定理可以通过库仑定律导出。 前页后页目录 4
前页 后页 目录 4 7.3 静电场的高斯定理 高斯定理 在静电场中,通过任意闭合曲面的电通量, 等于该曲面内电荷量的代数和除以真空中的介电 常数。 0 1 S S E S q d i = 内 闭合曲面S常称为高斯面。 高斯定理可以通过库仑定律导出

73静电场的高斯定理 球E.d5=∑a: 60S内 讨论 1.闭合曲面的电通量只与面内的电荷有关,但面上 各点的场强与面内、面外电荷都有关。 2闭合曲面的电通量为零,表示面内正负电荷代数 和为零,并不表示面内没有电荷。 3.电场线起始于正电荷,终止于负电荷。静电场是 有源场。 4高斯定理是静电场的一条基本规律,也适用于运 动电荷和迅速变化的电场。 前页后页目录 5
前页 后页 目录 5 7.3 静电场的高斯定理 0 1 S S E S q d i = 内 讨论 1.闭合曲面的电通量只与面内的电荷有关,但面上 各点的场强与面内、面外电荷都有关。 2.闭合曲面的电通量为零,表示面内正负电荷代数 和为零,并不表示面内没有电荷。 3.电场线起始于正电荷,终止于负电荷。静电场是 有源场。 4.高斯定理是静电场的一条基本规律,也适用于运 动电荷和迅速变化的电场
73静电场的高斯定理 二,高斯定理的应用 1.用高斯定理计算电通量 张Eds=∑a, 80S内 八、Eds 2a R 4 80 前页后页目录 6
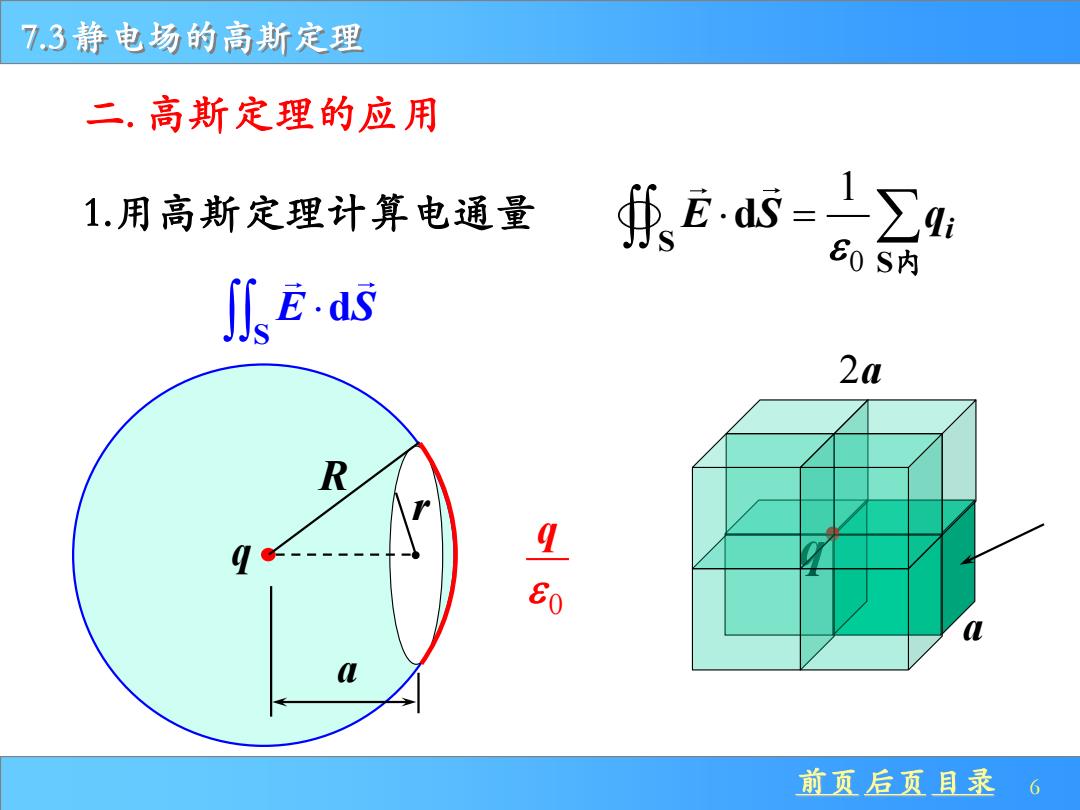
前页 后页 目录 6 7.3 静电场的高斯定理 q 1.用高斯定理计算电通量 二. 高斯定理的应用 a R r q a 2a 0 1 S S E S q d i = 内 S E S d 0 q

73静电场的高斯定理 求Eds-=∑g, 80S内 2用高斯定理计算电场强度 a.高斯面S上场强大小处处相等,场强方向处处 沿着面的法向。 求E·dS=求±EdS=±E球dS b.高斯面上,部分面S1上场强大小处处相等, 场强方向处处沿着面的法向。其余面S2上场强 方向处处沿着面的切向(或场强为零)。 fEas=八、E·ds+八,Eds=±E八ds 前页后页目录 7
前页 后页 目录 7 7.3 静电场的高斯定理 2.用高斯定理计算电场强度 0 1 S S E S q d i = 内 a.高斯面S上场强大小处处相等,场强方向处处 沿着面的法向。 S E S d S = E Sd S = E Sd b.高斯面上,部分面S1上场强大小处处相等, 场强方向处处沿着面的法向。其余面S2上场强 方向处处沿着面的切向(或场强为零)。 S E S d S1 = E S d S2 + E S d S1 = E Sd

73静电场的高斯定理 求Eds=∑q 60S内 条件:电荷分布具有特殊对称性,电场也具有特殊 对称性,有可能用高斯定理求得场强E。 关键:已知场强的对称性,选择合适的高斯面。求 出等式左边的积分。 前页后页且录 8
前页 后页 目录 8 7.3 静电场的高斯定理 条件:电荷分布具有特殊对称性,电场也具有特殊 对称性,有可能用高斯定理求得场强 。 关键:已知场强的对称性,选择合适的高斯面。求 出等式左边的积分。 E 0 1 i S S E S q d = 内
73静电场的高斯定理 例1均匀带电球面所激发的场强。(已知R,Q) 解:场强具有球对称性分布,方向沿径向。 作半径为r的同心球面作为高斯面。 承、E.a5=乐Eas =Ed ds =E.4πr2 ∑9 由高斯定理承Ed心=S q E= S内 4π6or 前页后页目录 9
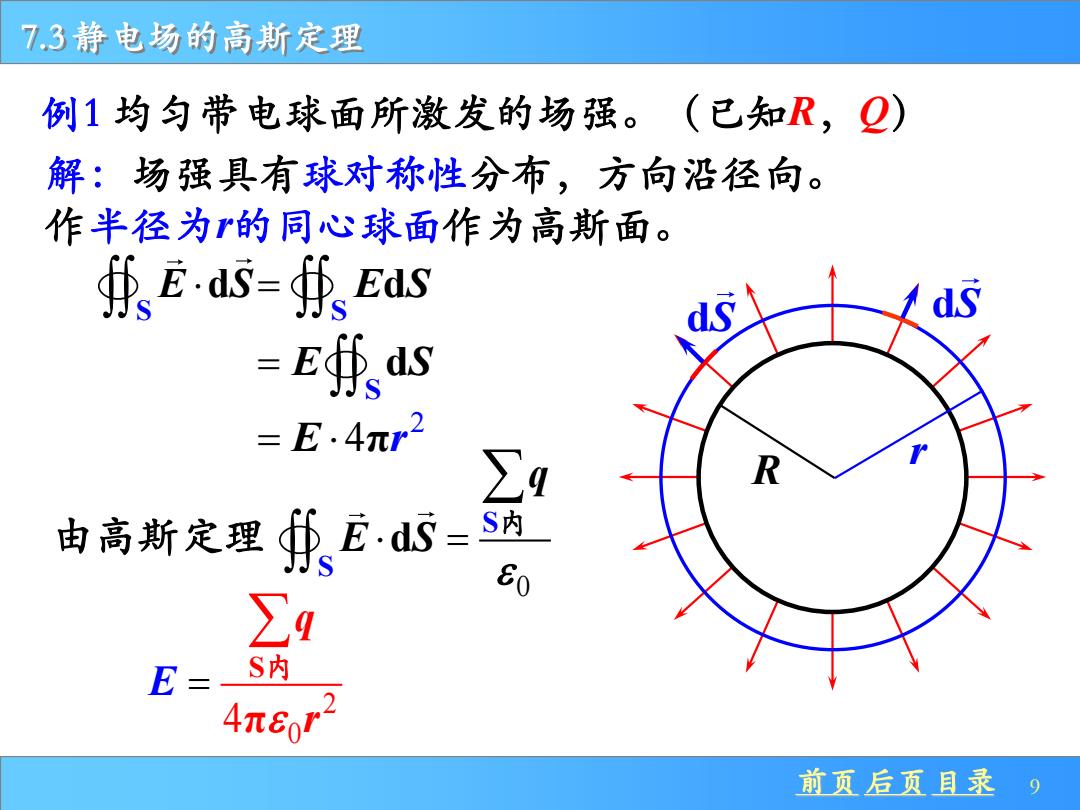
前页 后页 目录 9 7.3 静电场的高斯定理 R 2 0 4 S π r E q = 内 例1 均匀带电球面所激发的场强。(已知R,Q) 解:场强具有球对称性分布,方向沿径向。 作半径为r的同心球面作为高斯面。 S E S d 由高斯定理 0 S S d q E S = 内 r S dS = E Sd 2 = E 4πr S = E Sd dS
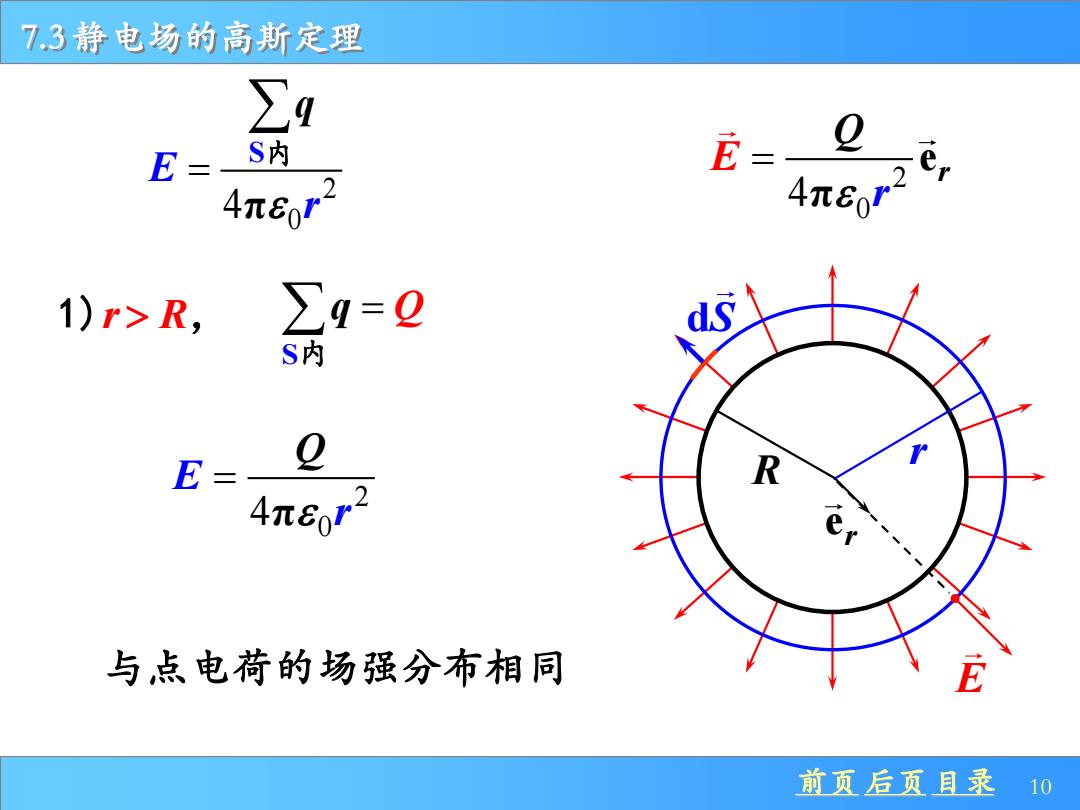
73静电场的高斯定理 ∑q E= S内 E--0 4π801 1)r>R, ∑4=0 S内 E= 4π801 与点电荷的场强分布相同 前页后页目录10
前页 后页 目录 10 7.3 静电场的高斯定理 R 2 0 4π E r Q = r dS 与点电荷的场强分布相同 S q = Q 内 1)r R, 2 0 4 S π E r q = 内 2 0 4 e π r Q E r = er E