
9.2动生电动势 9.2动生电动势 由导体运动产生的感应电动势 币=八Bds =八BuS ××a× =Blx dΦ UX = =-BI de 十 Bx dt dt × =-Blv X 方向b→a 前页后页目录 1
9.2 动生电动势 前页 后页 目录 1 由导体运动产生的感应电动势 S Φ = B Sd i d d Φ t E = − d d x Bl t = − = −Blv 方向b→a x B v d a c b l 9.2 动生电动势 = BlxS = B Sd

92动生电动势 导线内电子受到的洛仑兹力 F=-eixB 非静电场强 + F E=上=i×B × XX -e × E 十 根据电动势定义 b £=E·d b =(×Bdl =-Blv 前页后页目录 2
9.2 动生电动势 前页 后页 目录 2 v a b B 导线内电子受到的洛仑兹力 F e B = − v 非静电场强 k F E e = − = v B 根据电动势定义 i k L = E l d E b a = ( ) d B l v = −Blv b a = − B l d v

92动生电动势 动生电动势 £=L(ixB)d 闭合运动导线 号=∮(o×B)dM 正值一电动势方向沿积分方向。 前页后页目录 3
9.2 动生电动势 前页 后页 目录 3 动生电动势 i L = ( ) d B l E v 闭合运动导线 i L = ( ) d B l E v 正值——电动势方向沿积分方向
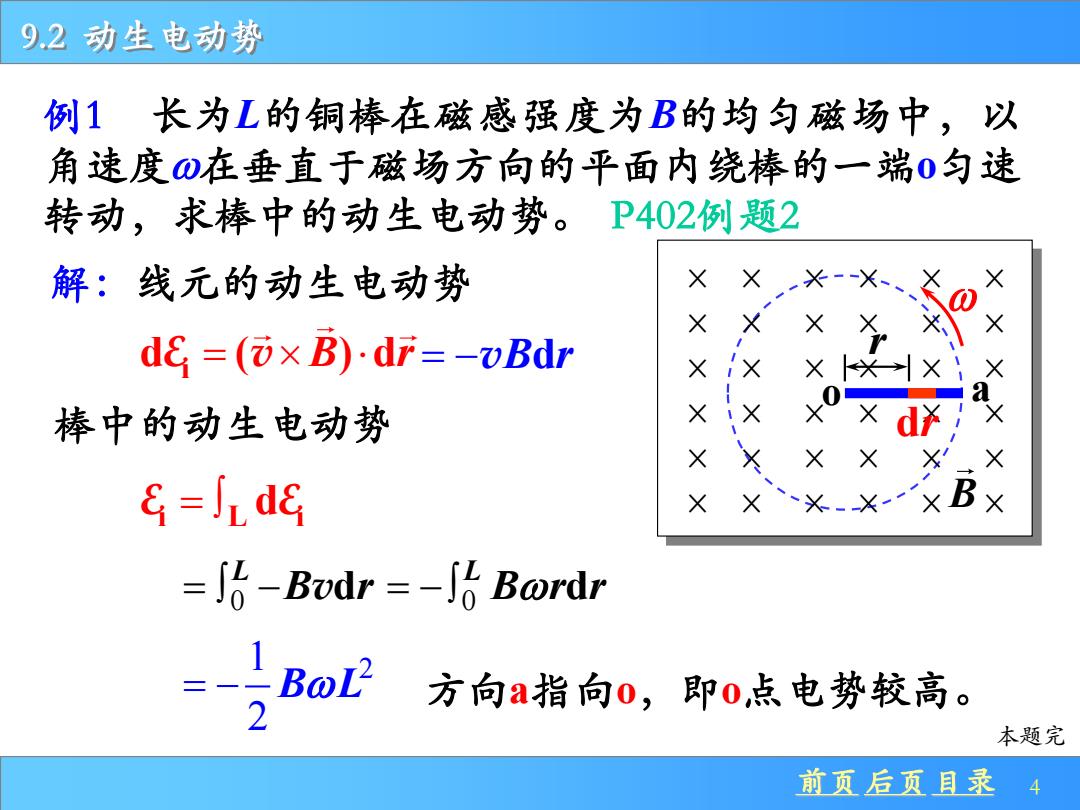
9.2动生电动势 例1长为L的铜棒在磁感强度为B的均匀磁场中,以 角速度⑩在垂直于磁场方向的平面内绕棒的一端0匀速 转动,求棒中的动生电动势。P402例题2 解:线元的动生电动势 de=(⑦×B)dF=-vBdr + 棒中的动生电动势 +0 a X d × =J d& =∫-Bvdr=-6 Bwrdr =-B2 2 方向指向0,即0,点电势较高。 本题完 前页后页目录4
9.2 动生电动势 前页 后页 目录 4 B o a 例1 长为L的铜棒在磁感强度为B的均匀磁场中,以 角速度在垂直于磁场方向的平面内绕棒的一端o匀速 转动,求棒中的动生电动势。 P402例题2 dr r 解:线元的动生电动势 d ( ) d Ei = v B r = −vB r d 棒中的动生电动势 E E i L i = d 0 d L = −B r v 1 2 2 = − B L 方向a指向o,即o点电势较高。 本题完 0 d L = − B r r

92动生电动势 例2长为I的直导线MN以速率v沿平行于长直载流导 线的方向运动,MN与载流导线共面,且相互垂直, 如图所示。设载流导线中的电流强度为I。导线M端 到载流导线的距离为a,求导线MIN中的动生电动势, 并判断哪端电势较高。P403例题3 解法一:用动生电动势公式求解 M de=(⑦×B)dr=-vBdr =-oodr dr 2πr =dr=+l -In 2nr 2π M端电势较高 前页后页目录5
9.2 动生电动势 前页 后页 目录 5 v a M N I 例2 长为l的直导线MN以速率v沿平行于长直载流导 线的方向运动,MN与载流导线共面,且相互垂直, 如图所示。设载流导线中的电流强度为I。导线M端 到载流导线的距离为a,求导线MN中的动生电动势, 并判断哪端电势较高。 P403例题3 r dr 解法一:用动生电动势公式求解 d ( ) d Ei = v B r = −vB r d 0 2 d π I r r = −v 0 2 MN d π a l a I r r + E = − v 0 2 ln π I a l a + = − v M端电势较高

92动生电动势 解法二:用电磁感应定律求解 回路MNo'oM的磁通量 M a -g xdr 2πr 0 Lolxa+l dr -n2 2πu EMN =-do ln(0+L) 2π M端电势较高 本节完 前页后页目录 6
9.2 动生电动势 前页 后页 目录 6 v a M N I o o x 解法二:用电磁感应定律求解 回路MNo'oM的磁通量 S Φ = B Sd 0 2 d π a l a I x r r + = 0 2 ln π Ix a l a + = MN d d Φ t E = − 0 2 ln( ) π I a l a + = − v M端电势较高 本节完 r dr