
11.3波动方程波速 11.3波动方程波速 一.波动微分方程 y=Acos 上式对x、t求二阶偏导数,得 前页后页目录 1
前页 后页 目录 1 11.3 波动方程 波速 一. 波动微分方程 上式对x、t 求二阶偏导数,得 11.3 波动方程 波速 0 cos x y A t u = − +

11.3波动方程波速 'y=-Ao'cos A 比较以上两式,得 平面波的波动方程 o2y 102y 省略推导 前页后页目录 2
前页 后页 目录 2 11.3 波动方程 波速 2 2 2 2 2 y y 1 x u t = 平面波的波动方程 省略推导 比较以上两式,得 2 2 2 2 0 cos y x A t x u u = − − + 2 2 2 0 cos y x A t t u = − − +

11.3波动方程波速 二.*波动方程的建立 细杆截面积S、密度p X+△x G+△G 9 △G= -△x y+△y O b' 应力的变化率 Ox 前页后页目录 3
前页 后页 目录 3 11.3 波动方程 波速 二. *波动方程的建立 细杆截面积S、密度 o x a b x x x + + x x x = x o 应力的变化率 y y y + a b x

11.3波动方程波速 体元ab上的合力 ∑F=-GS+(o+Ao)S +△G =△OS △= △x (00 Ax)S 由牛顿第二定律 ov '△x)S=pS△x 或 0o ov x 前页后页目录 4
前页 后页 目录 4 11.3 波动方程 波速 + x x x = 体元ab上的合力 = S ( ) x S x = 由牛顿第二定律 或 x t = v F S S = − + + ( ) ( ) x S S x x t = v

11.3波动方程波速 由杨氏模量定义 E=O σ △M/L 或o=E ay ay/ax Ox 上式求偏导数 00 Ox ar? 又因=@心 ov 8y 则 8t 上两式代入 &'y_po'y =P ,得 前页后页且录5
前页 后页 目录 5 11.3 波动方程 波速 由杨氏模量定义 E l l = y x = 或 y E x = 上式求偏导数 2 2 y E x x = 又因 y t = v 则 2 2 y t t = v 上两式代入 ,得 x t = v 2 2 2 2 y y x t E =

11.3波动方程 波速 E o2y 102y 又因 u= 所以 y= 是方程的解 一搬解=F+ 其中F和Φ为两个任意周期性函数。这个解包括 沿x正方向和X反方向的波,且不限于余弦波。 前页后页目录6
前页 后页 目录 6 11.3 波动方程 波速 又因 E u = 所以 2 2 2 2 2 y y 1 x u t = 0 cos x y A t u = − + 是方程的解 一般解 x x y F t Φ t u u = − + + 其中F 和为两个任意周期性函数。这个解包括 沿x正方向和x反方向的波,且不限于余弦波

11.3波动方程波速 三.*介质的形变及其模量 固体的体变模量 K=- p △V/V 应力p√ S 应变△V/W ■DHI川 流体的体变模量K=- △p △V/W 或K=-y av 前页后页目录 7
前页 后页 目录 7 11.3 波动方程 波速 三. *介质的形变及其模量 固体的体变模量 p K V V − 应力 f p S = 应变 V V 流体的体变模量 p K V V − 或 p K V V −
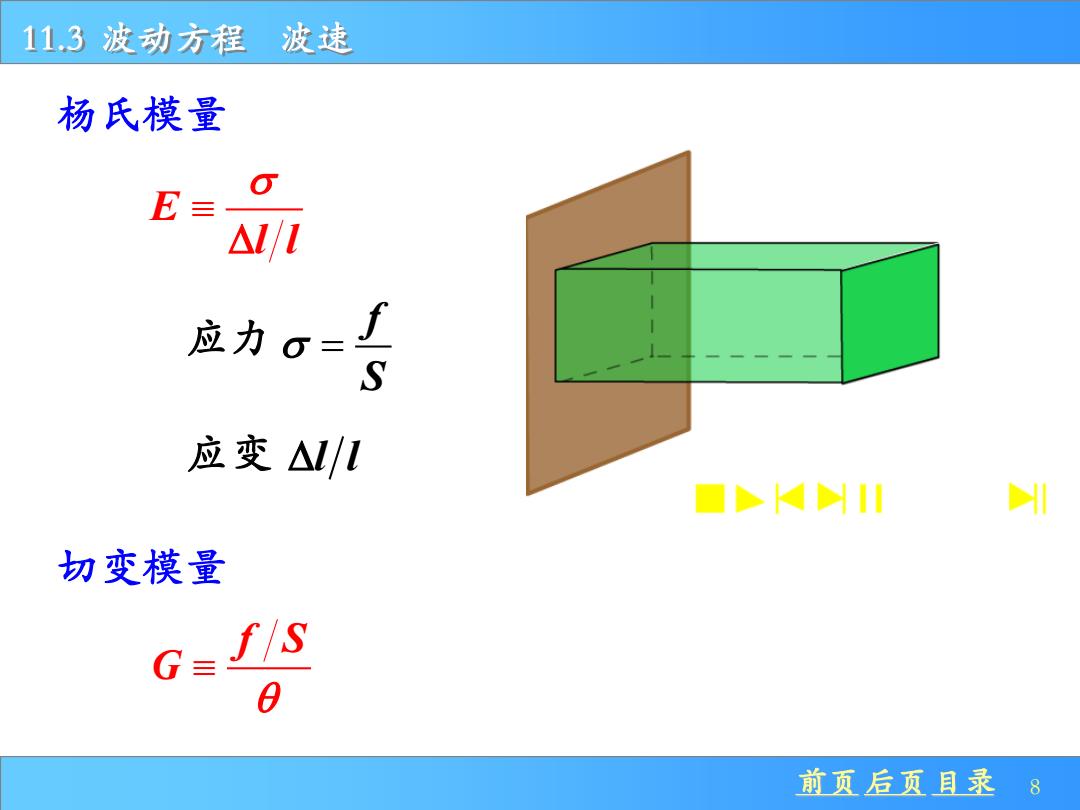
11.3波动方程波速 杨氏模量 E=O △M/1 应力。= S 应变△/I 口KHII 切变模量 G= 0 前页后页且录8
前页 后页 目录 8 11.3 波动方程 波速 杨氏模量 E l l 应力 f S = 应变 l l 切变模量 f S G

11.3波动方程波速 四.弹性介质中的波速 流体中纵波的波速 理想气体中纵波的波速“ Y为气体的比热容比 空气中声速约为340m/s。 前页后页目录9
前页 后页 目录 9 11.3 波动方程 波速 四. 弹性介质中的波速 流体中纵波的波速 K u = 理想气体中纵波的波速 p u = RT M = 为气体的比热容比 空气中声速约为340m/s

11.3波动方程波速 固体中横波的波速u G 固体中纵波的波速4 E 柔软绳索和弦中横波的波速“= F P P1为单位长度的质量 前页后页目录10
前页 后页 目录 10 11.3 波动方程 波速 固体中横波的波速 G u = 固体中纵波的波速 E u = 柔软绳索和弦中横波的波速 l F u = l 为单位长度的质量